Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

670 14 Electromagnetism II
Substituting (2) in (1)
u
B
=
1
2
μ H · H =
1
2
μ H
2
=
B
2
2μ
(3)
In free space μ = μ
0
. Therefore in vacuum
u
B
=
B
2
2μ
0
14.44
u
E
=
1
2
ε
0
E
2
(energy density in E-field) (1)
u
B
=
1
2
B
2
μ
0
(energy density in B-field) (2)
The fields for the plane wave are
E = E
m
sin(kx − ωt) (3)
B = B
m
sin(kx − ωt) (4)
Substituting (3) in (1) and (4) in (2)
u
E
=
1
2
ε
0
E
2
m
sin
2
(kx − ωt) (5)
u
B
=
1
2
B
2
m
μ
0
sin
2
(kx − ωt) (6)
Dividing (5) by (6)
u
E
u
B
=
ε
0
μ
0
E
2
m
B
2
m
(7)
But ε
0
μ
0
=
1
c
2
and E
m
= cB
m
∴
u
E
u
B
= 1oru
E
= u
B
14.45 By prob. (14.41) the magnetic energy stored in a coaxial cable
U
B
=
μ
0
i
2
l
4π
ln(b/a) (1)
where i is the current and l is the length of the cable. Further, its capacitance
is given by
C =
2πε
0
l
ln(b/a)
(2)

14.3 Solutions 671
The electric energy stored in the cable
U
E
=
1
2
ξ
2
C =
1
2
(i
2
R
2
)
2πε
0
l
ln(b/a)
(3)
By problem U
E
= U
M
.
∴
1
2
(i
2
R
2
)
2πε
0
l
ln(b/a)
=
μ
0
i
2
l
4π
ln(b/a) (4)
∴ R =
1
2π
μ
0
ε
0
ln(b/a) =
1
2π
4π ×10
−7
8.85 × 10
−12
ln(b/a)
=
376.7
2π
ln(b/a).
14.46 As the kinetic energy of proton (20 MeV) is much smaller than its rest mass
energy (938 MeV), non-relativistic calculations will be valid. In the classical
picture a charged particle undergoing acceleration ‘a’ emits electromagnetic
radiation. The electromagnetic energy radiated per second is given by
P =
q
2
a
2
6πε
0
c
3
(1)
Now a =
v
2
R
=
1
2
mv
2
2
mR
=
2K
mR
(2)
Substituting (2) in (1) and putting q = e for the charge of proton
P =
2e
2
K
2
3πε
0
c
3
m
2
R
2
(3)
The energy radiated per orbit is given by multiplying P by this time period
2π R/v = 2π R
√
m/2K
∴ K =
4e
2
K
3/2
3
√
2ε
0
c
3
m
3/2
R
=
4(1.6 × 10
−19
)
2
(20 × 1.6 × 10
−13
)
3/2
3
√
2(8.85 × 10
−12
)(3 × 10
8
)
3
(1.67 × 10
−27
)
3/2
(0.5)
= 1.89 ×10
−31
J = 1.18 × 10
−12
eV
which is quite negligible
14.47 Consider a sphere of radius r with its centre at the point source of power P.
Then the intensity of radiation at distance r will be I =
P
4πr
2
.

672 14 Electromagnetism II
I =
P
4πr
2
=
c ε
0
E
2
0
2
∴ E
0
=
P
2π r
2
cε
0
1/2
=
40
2π(1.0)
2
(3 ×10
8
× 8.85 × 10
−12
)
1/2
= 49 V/m
14.48
(a) I
0
=
P
A
=
1.2 × 10
−3
4 × 10
−6
= 300 W/m
2
(b) I
0
=
cε
0
E
2
0
2
→ E
0
=
2I
0
cε
0
1/2
=
2 × 300
3 × 10
8
× 8.85 × 10
−12
1/2
= 475 V/m
(c) B
0
=
E
0
c
=
475
3 × 10
8
= 1.58 ×10
−6
T = 1.58 μT
14.49
I =
P
A
=
P
πr
2
=
314 × 10
−3
3.14 × (0.5 × 10
−3
)
2
= 4 ×10
5
W/m
2
14.50 The average value of the Poynting vector < s > over a period of oscillation
of the electromagnetic wave is known as the radiant flux density, and if the
energy is incident on a surface it is called irradiance.
E = E
0
cos(kx − ωt), B = B
0
cos(kx − ωt)
∴ S = c
2
ε
0
E × B = c
2
ε
0
E
0
× B
0
cos
2
(kx − ωt)
∴
S
= c
2
ε
0
|
E
0
× B
0
|
;
cos
2
(kx − ωt)
<
But
;
cos
2
(kx − ωt)
<
=
1
T
T
0
cos
2
(kx − ωt)dt =
1
2
Further E⊥B and E
0
= cB
0
.
∴ < s >= I =
1
2
cε
0
E
2
0
=
1
2
E
2
0
μ
0
c
14.51
E
z
= 50 sin
4π ×10
14
t −
x
3 × 10
8
I =
cε
0
E
2
0
2
=
1
2
(3 × 10
8
)(8.85 × 10
−12
)(50
2
) = 0.066 W/m
2
14.52
|
E × H
|
=
|
E × B
|
μ
0
=
E
2
μ
0
c
(∵ B = E/c)
E ×H will be in the direction of S = (E × B)/μ
0
, which is the direction of
propagation.

14.3 Solutions 673
14.53
E
z
= 10 sin π
2 × 10
6
x − 6 ×10
14
t
= 10 sin
2π ×10
6
x − 6π × 10
14
t
Compare this with the standard equation
E
z
= E
z
0
sin(kx − ωt)
(a) ω = 2π f = 6π ×10
14
→ f = 3 × 10
14
Hz
(b) k = 2π × 10
6
→ λ = 2π/k = 10
−6
m
(c) v = ω/k = 6π ×10
14
/2π ×10
6
= 3 ×10
8
m/s
(d) E
z0
= 10 V/m
(e) The wave is linearly polarized in the z-direction and propagates along
the x-axis.
14.54 The wave propagates in the x-direction while the E-field oscillates along
the z-direction, that is, the E-field is contained in the xz-plane. Since B is
normal to both E and the direction of propagation it must be contained in the
xy-plane.
Thus, B
x
= B
z
= 0, and B = B
y
(x, t).NowB = E/c.
∴ B
y
(x, t) = 3.33 × 10
−8
sin π(2 × 10
6
x − 6 ×10
14
t) T
14.55 Let ν be the frequency of the incident microwave beam. Let the car be
approaching with speed v towards the observer. Then the frequency seen
by the car is given by the formula for Doppler shift
ν
= ν(1 +v/c) (1)
Upon reflection the microwave returns as if it was emitted by a moving
source travelling with speed v towards the observer. Therefore the observed
frequency is
ν
= ν
(1 + v/c) = ν(1 + v/c)
2
(2)
wherewehaveused(1).
ν = ν
− ν = ν(1 + v/c)
2
− ν = 2ν
v
c
1 +
v
2c
Assuming that v/c << 1
ν = 2ν
v
c
(beat frequency) (3)
For a receding car, proceeding along similar lines,
ν = ν
− ν =−2ν
v
c
(4)

674 14 Electromagnetism II
14.56 By prob. (14.55), ν = ν
− ν =−2ν
v
c
ν =−
2 × 800 × 10
6
3 × 10
8
×
5
18
× 90
=−133 Hz
14.57 The relation between the current i and the magnetic field B expressed as
5
B ·dl = μ
0
i is known as Ampere’s law. There are equal and opposite cur-
rents iin the conductors.
(a) r < a. The net current passing through the conductor bounded by the
closed path corresponds to that flowing through the inner conductor,
Fig. 14.7. Hence by Ampere’s theorem
Fig. 14.7 Magnetic field due
to current carrying coaxial
cylinder
B ·dl = (B)(2πr) = μ
0
i
(πr
2
)
πa
2
or B =
μ
0
ir
2πa
2
(b) a < r < b. Here the current through the outer conductor does not con-
tribute to B.
B ·dl = (B)(2πr) = μ
0
i
or B =
μ
0
i
2πr
(c) b < r < c. Here currents through both the conductors contribute to B.
B ·dl = (B)(2πr) = μ
0
i −μ
0
i
π(r
2
− b
2
)
π(c
2
− b
2
)
or B =
μ
0
i
2πr
(c
2
−r
2
)
(c
2
− b
2
)
(d) r > c. As the net current flowing through the closed path is zero, B = 0.
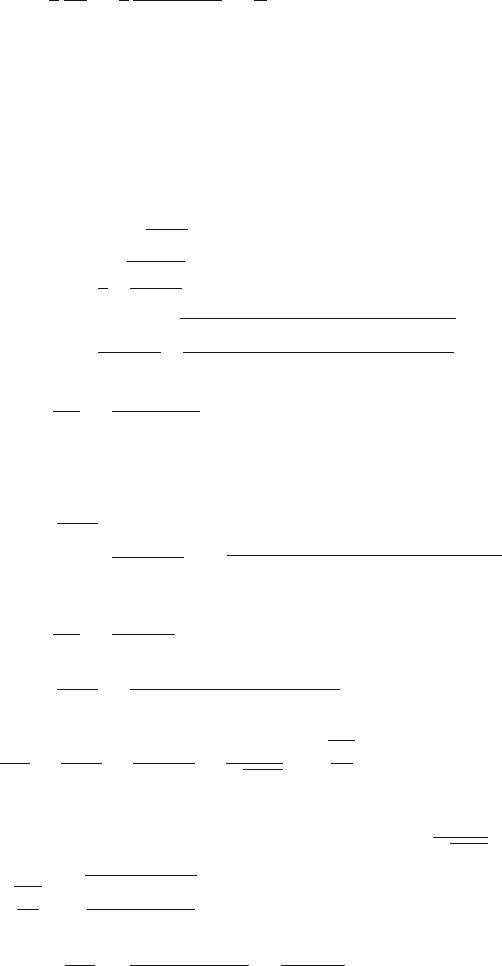
14.3 Solutions 675
14.58 Magnetic energy density
u
B
=
1
2
B
2
μ
0
=
1
2
4
2
4π ×10
−7
=
2
π
× 10
7
J/m
3
Energy stored in the magnetic field U
B
= u
B
× volume = u
B
πr
2
l
= 2 ×10
7
× 3
2
× 12.5 = 2.25 × 10
9
J
14.59 If P
0
is the power radiated by sun of radius r, then using the results of
prob. (14.51)
P
0
=
S
4πr
2
=
1
2μ
0
c
E
2
m
4πr
2
∴ E
m
=
1
r
P
0
μ
0
c
2π
∴ E
m
=
1
7 × 10
8
4 × 10
26
× 4π ×10
−7
× 3 × 10
8
2π
= 2.21 ×10
5
V/m
B
m
=
E
m
c
=
2.21 × 10
5
3 × 10
8
= 7.37 ×10
−4
T = 7.37 G
14.60 By prob. (14.51)
S
=
E
2
m
2μ
0
c
∴ E
m
=
2μ
0
c
S
=
2 × 4π × 10
−7
× 3 × 10
8
× 1300 = 990 V/m
14.61
B
m
=
E
m
c
=
300
3 × 10
8
= 1 ×10
−6
T
S
=
E
2
m
2μ
0
c
=
(300)
2
2 × 4π × 10
−7
× 3 × 10
8
= 119.4W/m
2
14.62
|
E
|
|
H
|
=
E μ
0
B
=
(Bc)μ
0
B
=
μ
0
√
μ
0
ε
0
=
μ
0
ε
0
where we have used the equations B = μ
0
H and c =
1
√
μ
0
ε
0
.
μ
0
ε
0
=
4π ×10
−7
8.85 × 10
−12
= 377
Units of
|
E
|
|
H
|
are
Volt /metre
Ampere/metre
=
Volt
Ampere
= Resistance
676 14 Electromagnetism II
14.63
Skin depth δ =
2
2π f σμ
0
μ
=
2
2π ×20 × 10
3
× 6 × 10
7
× 4π ×10
−7
× 1
= 4.6 ×10
−4
m = 0.46 mm
14.64
δ =
2
2π f σμ
0
μ
=
1
π ×3 × 10
8
× 5.6 × 10
7
× 4π ×10
−7
× 1
= 1.23 ×10
−4
m
= 0.123 mm = 3.88 μm
14.65 Let us begin with the ‘curl H’ Maxwell’s equation
∇ × H = J +
∂D
∂t
(1)
Assume that all the fields and currents in this equation are sinusoidal at a
single frequency ω. In that case (1) can be replaced by
∇ × H = J +jωD = J +jωεE (2)
where J is the current density, D = εE is the displacement vector and j is
imaginary
√
−1
.
The ‘curl E’ Maxwell’s equation is obtained in a similar way as (1).
∇ × E =−jωB (3)
Applying the curl operation to each side of (3)
∇ × (∇ × E) =−jω∇ × B (4)
Now ∇ × B can be replaced using (2) and the relation H = B/μ:
∇ × (∇ × E) =−jωμ(J + jωεE) (5)
We now use the vector identity
∇ × ∇ × E = ∇(∇ · E) =−∇
2
E (6)
Conductive materials do not contain any real charge density because any real
charge that many exist will repel itself and move outwards until it resides on

14.3 Solutions 677
the material’s outer surface. Therefore ∇ ·D = 0 and so also ∇ ·E = 0. Thus
the first term on the right by (6) vanishes. Therefore (5) becomes
∇
2
E = jωμ(J +jωεE) (7)
Assume that the material under consideration obeys Ohm’s law, J = σ
E
E,
where σ
E
is the conductivity. Then (7) becomes
∇
2
E = jωμ(σ
E
+ jωε)E (8)
For simplicity assume that the given material is an excellent conductor, so
that σ
E
>>
|
ωε
|
. In that case, the displacement current term, masked by the
conduction current, can be neglected, yielding
∇
2
E = jωμσ
E
E (9)
Since E = J/σ
E
we can write
∇
2
J = jωμσ
E
J (10)
Suppose the current flows through this material in the z-direction. The cur-
rent density is independent of x and y. In that case (10) simplifies to
∂
2
J
z
∂z
2
= jωμσ
E
J
z
(11)
which has the solution
J
x
= Ae
−(1+j)z/δ
+ Be
(1+j)z/δ
(12)
where A and B are constants, and δ given by
δ =
2
ωμσ
E
(13)
is known as the skin depth. Thus the magnitude of current density decreases
with depth. This effect is of practical importance as it affects resistive losses
accompanying a high-frequency current flow in an electronic circuit.
14.66 The average value of the Poynting vector is
S
=
1
2μ
0
E
m
B
m
=
1
2μ
0
E
m
E
m
c
=
E
2
m
2μ
0
c
=
10
−3
2
2 × 4π × 10
−7
× 3 × 10
8
= 1.327 ×10
−9
W/m
2
= 1.327 ×10
−13.
W/cm
2
.
678 14 Electromagnetism II
14.67 Poynting’s theorem is a mathematical statement based on Maxwell’s equa-
tions. The theorem is interpreted as energy balance equation in situations
where electromagnetic waves are present. We begin with the vector identity
∇ · (E ×H) = H · (∇ × E) − E ·(∇ ×H) (1)
We now make use of Maxwell’s ‘curl’ equations
∇ × E =−
∂B
∂t
(2)
∇ × H = J +
∂D
∂t
(3)
Substituting (2) and (3) in the RHS of (1)
∇ · (E ×H) =−H ·
∂B
∂t
− E ·
∂D
∂t
− E ·J (4)
which is the mathematical statement of Poynting’s theorem.
Further B = μH and D = εE (5)
∂
∂t
(E · E) =
∂
∂t
|
E
|
2
= 2E ·
∂E
∂t
(6)
Using (5) and (6) in (4) we obtain
∇ · (E ×H) =−
∂
∂t
ε
|
E
|
2
2
−
∂
∂t
μ
|
H
|
2
2
− E ·J (7)
We can integrate each side over any arbitrary volume V . Applying the diver-
gence theorem to the integral on the left
S
(E × H) · dS =−
ν
∂
∂t
ε
2
|
E
|
2
+
∂
∂t
μ
2
|
H
|
2
+ E ·J
dV (8)
and changing the sign of the equation and the order of differentiation and
integration we can rewrite (8) as
−
s
(E × H) · dS =
∂
∂t
V
ε
|
E
|
2
2
dV +
∂
∂t
V
μ
|
H
|
2
2
dV +
ν
E · J dV (9)
The first term on the right represents the rate of increase of electric energy
inside the volume V . The second term on the right represents the rate of
14.3 Solutions 679
increase of magnetic energy. The last term corresponds to the power con-
verted into Joule’s heat. Energy conservation demands that these three terms
be balanced by flow of energy into the volume and this is accounted for by
thetermontheleft.
The quantity S = E × H, representing the power density, is known as the
Poynting vector. The minus sign in (9) means that ds is the outward normal
and that (E ×H) ·ds represents power flowing outwards rather than inwards
for energy balance.
14.68 In one dimension the given equation reduces to
∂
2
E
∂x
2
− μ
0
ε
0
ε
r
∂
2
E
∂t
2
− μ
0
σ
N
∂E
∂t
= 0 (1)
Let the travelling wave be given by
E = E
0
e
i(kx−ωt)
(2)
∂
2
E
∂x
2
=−k
2
E,
∂ E
∂t
=−iωE and
∂
2
E
∂t
2
=−ω
2
E (3)
Inserting (3) in (1) and re-arranging and cancelling E
k
2
= μ
0
ε
0
ε
r
ω
2
+iμ
0
σ
N
ω (4)
14.69
F = x
2
z
3
ˆ
i
∇ × F =
ˆ
i
ˆ
j
ˆ
k
∂
∂x
∂
∂y
∂
∂z
x
2
z
3
00
= 3x
2
z
2
ˆ
j
∇×3x
2
z
2
ˆ
j =
ˆ
i
ˆ
j
ˆ
k
∂
∂x
∂
∂y
∂
∂z
03x
2
z
2
0
=−6x
2
z
ˆ
i +6xz
2
ˆ
k
∴ ∇×(∇×F) =−6x
2
z
ˆ
i +6xz
2
ˆ
k (1)
−∇
2
F =−
∂
2
∂x
2
+
∂
2
∂y
2
+
∂
2
∂z
2
x
2
z
3
ˆ
i =−(6 x
2
z + 2z
3
)
ˆ
i (2)
∇(∇·F) =−
ˆ
i
∂
∂x
+
ˆ
j
∂
∂y
+
ˆ
k
∂
∂z
ˆ
i
∂
∂x
+
ˆ
j
∂
∂y
+
ˆ
k
∂
∂z
· (x
2
z
3
ˆ
i)
=
ˆ
i
∂
∂x
+
ˆ
j
∂
∂y
+
ˆ
k
∂
∂z
(2xz
3
) = 2z
3
ˆ
i +6xz
2
ˆ
k (3)
