Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


650 14 Electromagnetism II
14.91 Show that the group velocity can be expressed as
v
g
=
c
n + ω
dn
dω
14.92 For a rectangular guide of width 2.5 cm what free-space wavelength of radi-
ation is required for energy to traverse 50 m of length of the guide in 1 μs.
What would be the phase velocity under these conditions?
14.93 Show that for light waves of angular frequency ω in a medium of refractive
index n, the group velocity v
g
and the phase velocity v
p
are related by the
expression
1
v
g
=
1
v
p
+
ω
c
dn
dω
where c is the velocity of light in free space.
[University of Manchester 1972]
14.94 Prove that the usual expression for the group velocity of a light wave in a
medium can be rearranged as v
g
= c
dv
d(nv)
, where c is the phase velocity of
the waves in free space, v is the frequency and n is the refractive index of the
medium.
[University of Durham 1961]
14.95 Show t hat the group velocity associated with a free non-relativistic particle
is the classical velocity of the particle.
[University of Manchester 1972]
14.96 Calculate the group velocity of light of wavelength 500 nm in glass for which
the refractive index μ at wavelength λ (meters) is
μ = 1.420 +
3.60 × 10
−14
λ
2
[University of Manchester 1972]
14.2.4 Waveguides
14.97 For a rectangular guide of width 2.5 cm, calculate (a) the phase velocity; (b)
the group velocity; (c) guide wavelength for the free-space wavelength of
4 cm. Assume the dominant mode.
14.98 A rectangular guide has a width a = 3 cm. What should be the free-space
wavelength if the guide wavelength is to be thrice the free-space wavelength?
14.99 (a) Calculate the guide wavelength for a rectangular waveguide of width a =
5 cm if the free-space wavelength is 8 cm. (b) What is the cut-off wavelength
for the guide?

14.3 Solutions 651
14.100 Calculate the number of states of electromagnetic radiation between 5000
and 6000 Å in wavelength using periodic boundary conditions in a cubical
region 0.5 cm on a side.
[University of Manchester 1972]
14.101 Consider a car entering a tunnel of dimensions 15 m wide and 4 m high.
Assuming the walls are good conductors, can AM radio waves (530–
1600 kHz) propagate in the tunnel?
[The University of Aberystwyth, Wales 2006]
14.102 Calculate the least cut-off frequency for TE
mn
waves for a rectangular
waveguide of dimensions 5 cm ×4cm.
14.103 Calculate how the wave and group velocities of the TE
01
wave in a rectan-
gular waveguide with a = 1 cm and b = 2 cm vary with frequency.
[The University of Wales, Aberystwyth 2004]
14.104 Consider a rectangular waveguide of dimensions x = a and y = b,the
TM
mn
wave travelling in the z-direction which is the axis of the guide.
Given that the z-component E
z
satisfies the equation
∂
z
∂x
z
+
∂
z
∂y
z
E
z
= (k
2
− ω
2
με)E
z
obtain (a) the solution for E
z
and (b) the cut-off frequency.
14.105 Consider a rectangular waveguide of dimensions x = a and y = b,the
wave travelling along the z-direction, the axis of the guide. Given that the
z-component H
z
satisfies the equation
∂
2
∂x
2
+
∂
2
∂y
2
H
z
= (k
2
− ω
2
με)H
z
(a) obtain the solution for H
z
. (b) Obtain the cut-off frequency. (c) What are
the similarities and differences between TM
mn
mode and TE
mn
mode?
14.3 Solutions
14.3.1 The RLC Circuits
14.1 (a) Reactance of capacitor
X
c
=
1
2πfc
=
1
2π ×(1000/2π) × 2.5 × 10
−6
= 400
Impedance of the circuit
Z =
R
2
+ X
2
c
=
(300)
2
+ (400)
2
= 500
652 14 Electromagnetism II
The rms current, I
e
=
V
e
Z
=
50
500
= 0.1A
PD across the capacitor, V
c
= I
e
X
c
= 0.1 ×400 = 40 V
(b)
Power, P = V
e
I
e
cos α = V
e
I
e
R
Z
= 50 ×0.1 ×
300
500
= 3.0W
14.2 (a)
X
L
= 2π fL = 2π ×
200
π
× 10 × 10
−3
= 4
Z =
R
2
+ X
2
=
3
2
+ 4
2
= 5
I
e
= V
e
/Z = 5/5 = 1.0A
V
R
= I
e
R = 1.0 × 3 = 3.0V
V
L
= I
e
X
L
= 1.0 ×4 = 4.0V
(b) Phase angle between V
e
and I
e
is given by
tan α =
X
L
R
=
4
3
⇒ α = 53
◦
V
e
leads I
e
by 53
◦
14.3
U =
1
2
LI
2
L =
2U
I
2
=
2 × 10
5
2
= 0.8H
14.4
(a) f =
1
2π
√
LC
=
1
2π
√
4 × 10
−6
× 5 × 10
−11
= 1.125 ×10
−7
Hz
(b) λ =
c
f
=
3 × 10
8
1.125 × 10
7
= 26.67 m
14.5 (a) Z =
(X
L
− X
C
)
2
+ R
2
=
(12 − 20)
2
+ 6
2
= 10
(b) P = I
e
V
e
R
Z
=
V
2
e
R
Z
2
=
(250)
2
× 6
10
2
= 3750 W
14.6 At ω
0
= 600 rad/s, X
L
= X
C
∴ ω
0
L =
1
ω
0
C
⇒
1
LC
= ω
2
0
At ω = 60 rad/s,
X
C
X
L
=
1/ωc
ωL
=
1
ω
2
LC
=
ω
2
0
ω
2
=
(600)
2
60
2
= 100
14.3 Solutions 653
14.7
(a)
X
C
=
1
ωC
=
1
2π fC
C =
1
2π fX
C
=
1
2π ×250 × 4
= 1.57 ×10
−4
F
(b) X
C
=
1
2π f
C
=
1
2π ×100 × 1.57 × 10
−4
= 10
(c) I
e
=
V
e
X
C
=
220
10
= 22 A
14.8
V
e
I
e
=
ω
2
L
2
+ R
2
=
4π
2
f
2
L
2
+ R
2
∴
12
0.05
=
4π
2
× (50)
2
L
2
+ R
2
(1)
Also tan α =
ωL
R
=
2πfL
R
∴ tan 60
◦
=
√
3 = 2π ×50
L
R
(2)
Solving (1) and (2) we find R = 120 and L = 0.66 H.
When the capacitor of capacitance C is connected in series with the above
circuit α = 0.
tan α = tan 0
◦
=
1
R
ωL −
1
ω c
∴ C =
1
ω
2
L
=
1
(2π ×50)
2
× 0.66
= 15.37 ×10
−6
F = 15.37 μF
14.9
(a) The rms current, I
e
=
V
e
ωL
=
V
e
2πfL
=
220
2π ×50 × 0.6
= 1.17 A
(b) Peak current, I
0
=
√
2I
e
= 1.414 ×1.17 = 1.65 A.
14.10
(a) I
e
=
V
e
4π
2
f
2
L
2
+ R
2
=
24
4π
2
× (50)
2
× (0.01)
2
+ 4
2
= 4.72 A
(b) Power, P = I
2
e
R = (4.72)
2
× 4 = 89 W
(c) V
R
= I
e
R = 4.72 × 4 = 18.88 V
V
L
= 2π fLI
e
= 2π × 50 × 0.01 ×4.72 = 13.82 V
14.11
V = V
m
sin ωt
0.5 V
m
= V
m
sin
2π f
1
360
∴
2π f
360
=
π
6
⇒ f = 30 Hz

654 14 Electromagnetism II
14.12 For the parallel RLC circuit, Fig. 14.1
Q = CV, I
2
=−
dQ
dt
=−C
dV
dt
V = R
p
(
I
2
+ I
1
)
=−L
dI
1
dt
dV
dt
= R
p
dI
2
dt
+
dI
1
dt
=−CR
p
d
2
V
dt
2
− R
p
V
L
∴
d
2
V
dt
2
+
1
R
p
C
dV
dt
+
V
LC
= 0 (parallel arrangement)
Compare the above equation with the given equation
d
2
V
dt
2
+
R
L
dV
dt
+
V
LC
= 0
∴ R
p
=
L
CR
.
14.13 We can find the dimensions of μ
0
and ε
0
from the following set of formulae:
F = ilB (force on the current-carrying wire) (1)
B =
μ
0
i
2πr
(magnetic field due to a current-carrying wire) (2)
F =
Q
2
4πε
0
r
2
(electrostatic force between charges) (3)
i = Q/t (4)
Combining (1)–(4), [μ
0
ε
0
]=[T
2
/L
2
]
or
1
√
μ
0
ε
0
=
L
T
=[v]=[c]
14.14 We first derive the dimensional formulae for R, C and L from the defining
equation Power = i
2
R
[Power]=[Ml
2
T
−3
]=[A
2
R]=[A
2
][R]
∴ [R]=[Ml
2
T
−3
A
−2
] (1)
Energy of a capacitor E =
1
2
Q
2
C
and Q = it
∴ [C]=[M
−1
l
−2
T
4
A
2
] (2)
14.3 Solutions 655
Energy of an inductance, E =
1
2
Li
2
∴ [L]=[Ml
2
T
−2
A
−2
] (3)
Using (1), (2) and (3), it is observed that the given combinations have the
dimension of time and therefore are expressed in seconds
[
RC
]
=
L/R
=
√
LC
=
[
T
]
14.15
ω =
1
√
LC
(1)
ω
=
1
LC
−
R
2L
2
(2)
ω − ω
ω
= 1 −
ω
ω
= 1 −
1 −
R
2
C
4L
1 −
1 −
R
2
C
8L
=
R
2
C
8L
(3)
where we have used (1) and (2) and expanded the radical binomially.
q = q
m
e
−Rt /2L
, q/q
m
=
1
2
whence t =
2L
R
ln
q
m
q
=
2L
R
ln 2 (4)
If n is the number of cycles and ν the oscillating frequency
t =
n
ν
= 2π n
√
LC =
2L
R
ln 2
or
CR
2
L
=
(ln 2)
2
(πn)
2
(5)
Combining (3) and (5)
ω − ω
ω
=
ω
ω
=
(ln 2)
2
8π
2
n
2
=
0.006085
n
2
= 0.00038
where we have put n = 4.
14.16 q = q
m
e
−Rt /2L
cos ω
t (charge oscillation of damped oscillator)
Differentiating with respect to time
i =
dq
dt
=−q
m
ω
e
−Rt /2L
R
2Lω
cos ω
t + sin ω
t
=−q
m
ω
e
−Rt /2L
(tan φ cos ω
t + sin ω
t)
656 14 Electromagnetism II
where we have set R/2Lω
= tan φ. This gives
i =
−q
m
ω
e
−Rt /2L
cos φ
(sin φ cos ω
t + cos φ sin ω
t)
=−q
m
ω
e
−Rt /2L
sin(ω
t + φ)
cos φ
But for low damping φ → 0asR/2Lω
→ 0.
∴ cos φ → 1, so that
i =−q
m
ω
e
−Rt /2L
sin(ω
t + φ)
14.17 Equation of the circuit is
L
d
2
q
dt
2
+
1
C
q = ξ (1)
Multiply (1) by i = dq/dt
Li
di
dt
+
1
C
q
dq
dt
= ξ t
or
d
dt
1
2
Li
2
+
d
dt
q
2
2C
= P
input
(2)
Thus, the input power is the sum of the powers delivered to the inductor and
the capacitor.
14.18 The circuit equation is
L
d
2
q
dt
2
+ R
dq
dt
+
1
C
q = 0(1)
Multiply (1) by i =
dq
dt
Li
di
dt
+ Ri
2
+
1
C
q
dq
dt
= 0
or
d
dt
1
2
Li
2
+
q
2
2C
=−Ri
2
or
dE
dt
=−i
2
R (2)
where E =
1
2
Li
2
+
q
2
2C
= total energy

14.3 Solutions 657
14.19 If U is the total field energy then
U = U
B
+U
E
=
1
2
Li
2
+
1
2
Q
2
C
(1)
which shows that at any time the energy is stored partly in the magnetic
field in the conductor and partly in the electric field in the capacitor. In the
presence of the resistance R the energy is transferred to Joule heat, being
given by
dU
dt
=−i
2
R (2)
the minus sign signifying that the stored energy U decreases with time. Dif-
ferentiating (1) with respect to time and equating the result with (2) gives
Li
di
dt
+
Q
C
dQ
dt
=−i
2
R (3)
Substituting i = dQ/dt and di/dt = d
2
Q/dt
2
, (3) becomes
d
2
Q
dt
2
+
R
L
dQ
dt
+
Q
LC
= 0(4)
Writing R/L = 2γ and 1/LC = ω
2
0
, (4) takes the required form
d
2
Q
dt
2
+ 2γ
dQ
dt
+ ω
2
0
Q = 0(5)
(a) f
0
=
1
2π
√
LC
=
1
2π
√
80 × 10
−3
× 700 × 10
−12
= 2.128 ×10
4
Hz
(b) τ =
L
R
=
80 × 10
−3
100
= 8 ×10
−4
s
14.20
d
2
Q
dt
2
+ 2γ
dQ
dt
+ ω
2
0
Q = 0(1)
Let Q = e
λt
so that dQ/dt = λe
λt
and d
2
Q/dt
2
= λ
2
e
λt
.
The characteristic equation is then
λ
2
+ 2γλ+ ω
2
0
= 0
whose roots are λ =−γ ±
γ
2
− ω
2
0
(2)
Calling α =
γ
2
− ω
2
0
λ
1
=−γ + α, λ
2
=−γ − α

658 14 Electromagnetism II
The general solution becomes
Q = C
1
e
(−γ +α)t
+ C
2
e
(−γ −α)t
(3)
The constants C
1
and C
2
are determined from the initial conditions. Suppose
at t = 0, Q = Q
0
and
i = dQ/dt = 0
Q
0
= C
1
+C
2
(4)
dQ
dt
= C
1
(−γ + α) − C
2
(γ + α) = 0(5)
Solving (4) and (5), C
1
= Q
0
(γ + α)/2α and C
2
= Q
0
(α − γ)/2α
Substituting C
1
and C
2
in (3)
Q =
1
2
Q
0
e
−γ t
(1 + γ/α)e
αt
+ (1 − γ/α)e
−αt
(6)
For underdamping condition resistance R is small so that γ<ω
0
and α is
imaginary and may be written as α = jω
, where j is imaginary. The roots
of the characteristic equation are complex conjugate.
ω
2
= ω
2
0
− γ
2
(7)
Equation (6) reduces to
Q = Q
0
e
−γ t
[cos ω
t + (γ /ω
) sin ω
t] (8)
Calling sin ε =−γ/ω
0
and cos ε = ω
/ω
0
, (8) becomes
Q =
ω
0
Q
0
ω
e
−γ t
cos(ω
t + ε) (9)
or Q = Ae
−γ t
cos(ω
t + ε) (10)
where the amplitude A = ω
0
Q
0
/ω
and the phase ε = tan
−1
(−γ/ω
).
The constants A and ε which are real are determined by initial conditions.
Equation (9) represents a damped harmonic motion of period
T
=
2π
ω
2
0
− γ
2
(11)
As in the case of an undamped oscillation, the frequency is independent of
the amplitude but is always lower than that of the undamped oscillator. The
amplitude of oscillations Ae
−γ t
decreases exponentially and is no longer
constant.
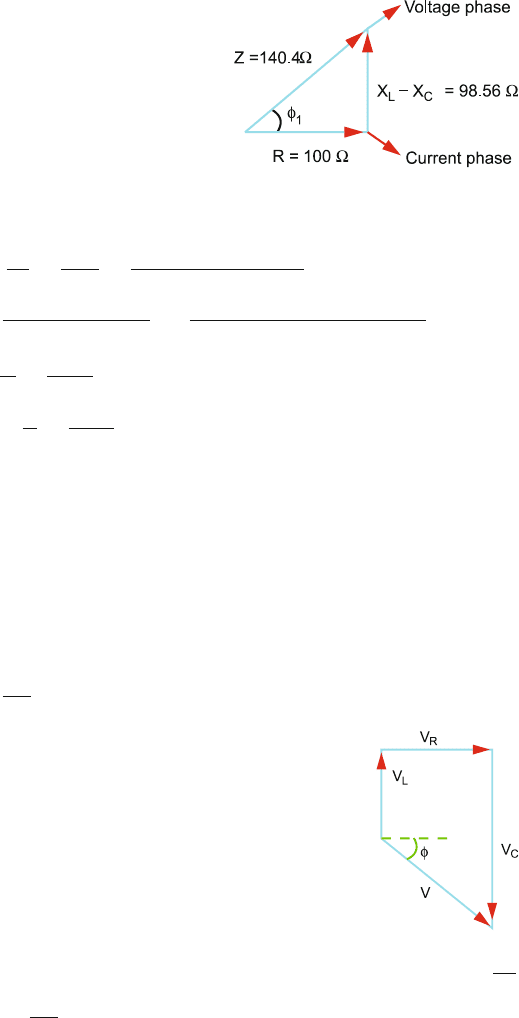
14.3 Solutions 659
14.21 Phasor diagram, Fig. 14.5
Fig. 14.5
(i) X
L
= ωL = 2πfL = (2π)(80)(0.2) = 100.48
X
C
=
1
ωc
=
1
2πfc
=
1
(2π)(80)(10 × 10
−6
)
= 199.04
(ii) Z =
R
2
+ (X
L
− X
C
)
2
=
(100)
2
+ (100.48 − 199.04)
2
=140.4
(iii) I
T
=
V
Z
=
600
140.4
= 4.27 A(rms)
(iv) cos ϕ =
R
Z
=
100
140.4
= 0.71225 → ϕ = 44.58
◦
(v) V
R
= I
T
R = 4.27 × 100 = 427 V
rms
V
C
= I
T
X
C
= 4.27 ×199.04 = 850 V
rms
V
L
= I
T
X
L
= 4.27 ×100.48 = 429 V
rms
V
2
= V
2
R
= (V
L
− V
C
)
2
The voltages on R, C and L are shown in the phasor diagram, Fig. 14.6.
Here the voltage lags the current as X
C
> X
L
.
(vi) ω
2
=
1
LC
Fig. 14.6
(vii) The circuit will be in resonance when X
L
= X
C
, that is, ωL =
1
ωc
or ω
2
=
1
LC
.
