Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


620 13 Electromagnetism I
13.54 For equilibrium, magnetic force = gravitational force.
F =
μ
0
li
1
i
2
2π d
= mg
∴ d =
μ
0
li
1
i
2
2πmg
=
4π ×10
−7
× 2 × 10 × 15
2π ×4 × 10
−3
× 9.8
= 1.53 ×10
−3
m
= 1.53 mm
13.55
(a) Net force per metre on the outer wire
F
l
=
F
1
l
+
F
2
l
=
μ
0
i
1
i
3
2 π d
+
μ
0
i
2
i
3
2 π × 2d
=
μ
0
i
3
(2i
1
+i
2
)
4π d
=
4π ×10
−7
× 20(2 × 20 + 20)
4π ×0.1
= 1.2 ×10
−3
N
(b) Zero
13.56 F = ilB + (i)(π R)B + ilB = i(2l +π R)B.
13.57
(i) The force on the horizontal segments is zero as they are perpendicular
to the straight wire. For the vertical segments the force is repulsive for
antiparallel currents and attractive for parallel currents, the magnitude
being
F =
μ
0
li
1
i
2
2πd
(1)
where d is the distance of separation.
Force on the nearer vertical segment
F
1
=−
(4π ×10
−7
)(0.1)(20)(5)
(2π)(0.02)
=−1 × 10
−4
N
Force on the farther vertical segment
F
2
=+
(4π ×10
−7
)(0.1)(20)(5)
(2π)(0.07)
=+2.86 × 10
−5
N
(ii) The net force on the coil, F
net
= F
1
+ F
2
=−7.14 × 10
−5
N
13.58
(a) Wire PQ will produce a field of induction B
1
at the segment AB of the
coil. The magnitude of B
1
will be
B
1
=
μ
0
I
1
2π d
(1)
The right-hand rule shows that the direction of B
1
at the segment AB
is down, wire AB, which carries a current I
2
finds itself immersed in
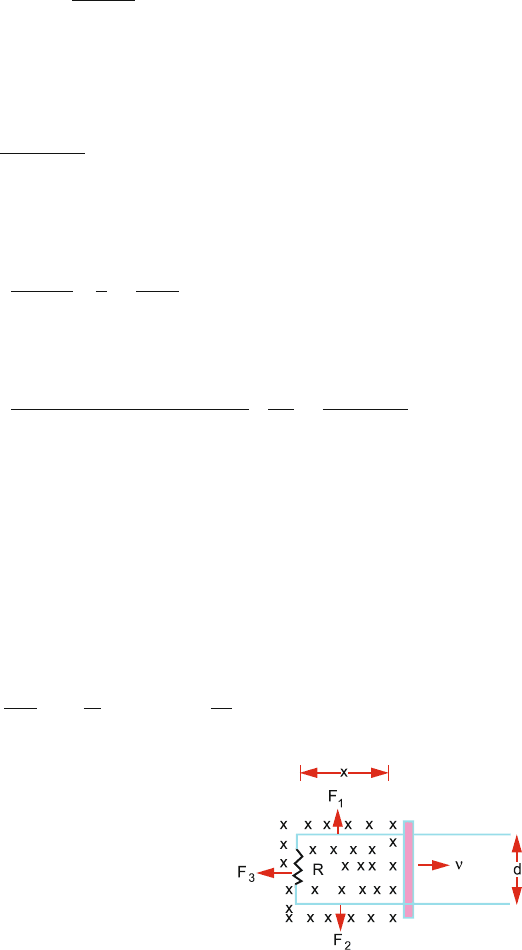
13.3 Solutions 621
an external field of magnetic induction B
1
. A length l of the segment
AB will experience a sideway magnetic force equal to il × B whose
magnitude is
F
2
= I
2
lB
1
=
μ
0
lI
1
I
2
2πd
(2)
The vector rule of signs shows that F
2
lies in the plane of the coil and
points to the right. A similar reasoning shows that the force on the seg-
ment CD will be
F
3
=
μ
0
lI
1
I
2
2π(d +l)
(3)
to the left in the plane of the coil. There is no force on the segments BC
and AD as they are perpendicular on PQ:
F
net
=
μ
0
lI
1
I
2
2π
1
d
−
1
d +l
(4)
to the right
F
net
=
(4π ×10
−7
)(0.05)(1)(4)(10)
2π
1
0.1
−
1
0.1 + 0.05
= 1.335 ×10
−5
N
where we have multiplied (4) by 10 for the number of coils.
13.59
(a) The flux φ
B
enclosed by the loop, Fig. 13.30,is
φ
B
= Blx (1)
where lx is the area of that part of the loop in which B is not zero. By
Faraday’s law
ξ =−
dφ
B
dt
=−
d
dt
(Blx) =−Bl
dx
dt
= Bl v (2)
Fig. 13.30

622 13 Electromagnetism I
where the speed v =−dx/dt for the speed with which the connecting
rod is pulled out of the magnetic field. The emf Blv sets up a current in
the loop given by
i =
ξ
R
=
Blv
R
(3)
(b) The total power delivered to the resistor is just the Joule heat given by
P
I
= i
2
R =
B
2
l
2
v
2
R
Note that energy conservation tells us that for steady motion of the rod
the external agent must provide power equal to the Joule heat. That this
is so is borne out from
P = F
3
v =
B
2
l
2
v
2
R
·
(c) The current the loop produces forces F
1
, F
2
and F
3
on the three sides of
the loop in accordance with
F = il ×B (4)
Because F
1
and F
2
are equal and opposite, they cancel each other, while
F
3
which opposes the motion of the sliding rod is given by (4) and (3) in
magnitude as
F
1
= ilB sin 90
◦
=
B
2
l
2
v
R
(5)
13.3.4 Magnetic Energy, Magnetic Dipole Moment
13.60 Elementary magnetic moment
dμ = (di)(dA) =
ω qr dr
π R
2
(π r
2
) =
ω qr
3
dr
R
2
where dA is the area enclosed by r and the value of di is used from (2) of
prob. (13.37).
Therefore the magnetic moment of the disc is
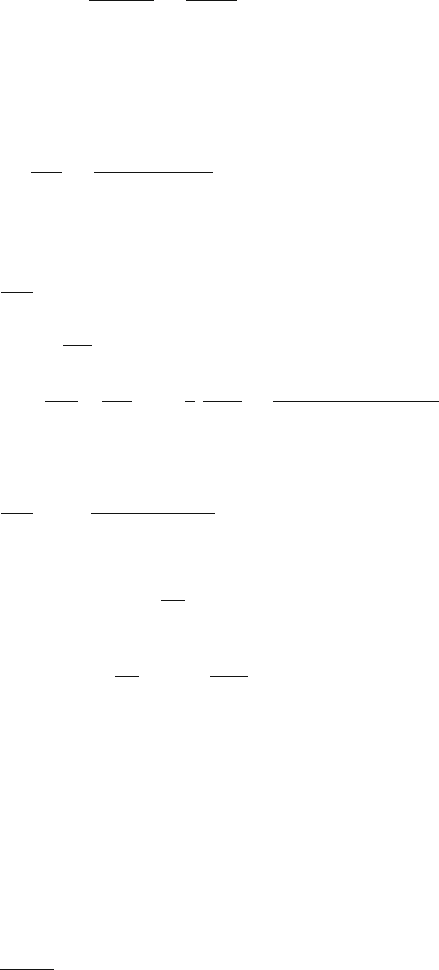
13.3 Solutions 623
μ =
dμ =
R
0
ω qr
3
dr
R
2
=
ω qR
2
4
13.61 Magnetic moment
μ = NiA = (1)(i)(πr
2
)
∴ i =
μ
πr
2
=
6.4 × 10
21
π(6.4 × 10
6
)
2
= 4.98 ×10
7
A
13.62 Magnetic energy density
u
B
=
1
2μ
0
B
2
But B =
μ
0
i
2r
∴ u
B
=
1
2μ
0
μ
0
i
2r
2
=
1
8
μ
0
i
2
r
2
=
4π ×10
−7
× (100)
2
8 × (0.1)
2
= 0.157 J/m
3
13.63 u
B
=
1
2μ
0
B
2
=
(13.5)
2
2 × 4π × 10
−7
= 7.25 ×10
7
J/m
3
13.64 τ
max
= iAB = (i)(πr
2
) B
But l = 2πr → r =
l
2π
∴ τ
max
= π i
l
2π
2
B =
l
2
iB
4π
13.65 Let the sphere of radius R rotate about the z-axis, Fig. 13.31. Consider a
spherical shell of radius r(r < R) concentric with the sphere. Consider a
volume element symmetrical about the z-axis.
dV = 2πr
2
sin θ d θ dr (1)
where θ is the polar angle and r is the distance of the volume element from
the centre. The charge dq residing in the volume element is
dq =
3 q
4 π R
3
dV (2)
The current due to rotation of charge is
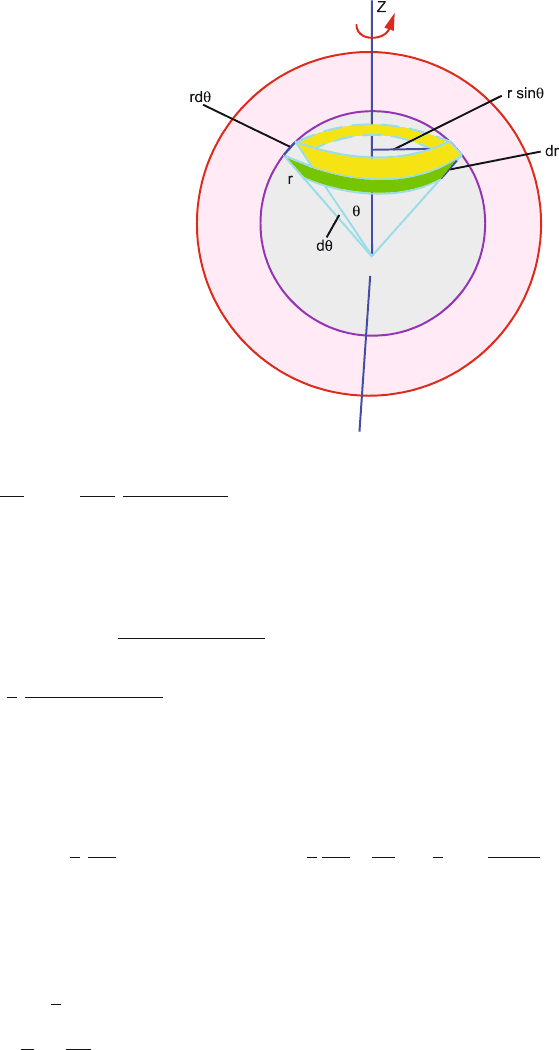
624 13 Electromagnetism I
Fig. 13.31 Magnetic moment
due to a rotating charged
sphere
di =
ω
2π
dq =
3qω
4π
r
2
sin θ dθ dr
R
3
(3)
where we have used (2) and (1).
The magnetic moment due to di is
dμ = (di)(dA) =
3q ωr
2
sin θ dθ dr
4π R
3
(π r
2
sin
2
θ)
=
3
4
ω qr
4
dr sin
3
θ dθ
R
3
(4)
where dA is the area enclosed by the circle of radius r sin θ .
Total magnetic moment
μ =
dμ =
3
4
ω q
R
3
R
0
r
4
dr
π
0
sin
3
θ dθ =
3
4
ω q
R
3
R
5
5
4
3
=
ω qR
2
5
(5)
The angular momentum of a sphere about a diameter is
L = I ω =
2
5
mR
2
ω (6)
∴
μ
L
=
q
2m
(7)

13.3 Solutions 625
13.66 U =−p · E =−pE cos θ =−(1.6 × 10
−29
)(1000) cos 30
◦
=−1.38 ×
10
−26
J.
13.3.5 Faraday’s Law
13.67
dr
dt
α t (by problem) (1)
ξ =−
dφ
dt
=
d
dt
(BA)(by Faraday’s law) (2)
But B ∝
1
r
and A = πr
2
(3)
∴ ξ ∝
dr
dt
(4)
or ξ ∝ t (5)
wherewehaveused(1)
13.68 0.4Oe= 0.4 × 80 A/m = 32 A/m
B = μ
0
H = 4π ×10
−7
× 32 = 4.02 × 10
−5
T
v = 720 km/h = 200 m/s
ξ = Blv = 4.02 × 10
−5
× 30 × 200 = 0.24 V
13.69 V = πr
2
Bf = π(0.1)
2
× 2 × 10
−5
× 5 = 3.14 × 10
−6
V
13.70 R =
BAN
q
=
0.1 × 0.001 × 30
10
−5
= 300
13.71 ξ =−
φ
t
=
AB
t
=
0.2 × 0.25
10
−4
= 500 V
i =
ξ
R
=
500
20
= 25 A
13.72 The amplitude of the induced voltage
ξ
0
= ω BA = 2πfBA = 2π ×40 ×0.5 × (0.25)
2
= 7.85 V
Amplitude of the induced current
I
0
=
ξ
0
R
=
7.85
4
= 1.96 A
13.73 ξ = iR = 0.4 × 5 = 2V

626 13 Electromagnetism I
ξ = vlB
∴ v =
ξ
lB
=
2
0.2 × 1.0
= 10 m/s
13.74 ξ =−
dφ
dt
=−
AdB
dt
A = area of the triangle sandwiched between the ends of the rod and the
radii connecting the centre with the ends, Fig. 13.18:
A =
1
2
(base)(altitude) =
1
2
l
R
2
− (l/2)
2
Thus ξ =−
dB
dt
l
2
R
2
− (l/2)
2
13.75 Gravitational force on the loop
F
g
= mg sin θ
Magnetic force on the loop
F
m
= (B cos θ)il = B cos θ
ξ l
R
=
B cos θ l
R
v B cos θ ·l =
v B
2
l
2
cos
2
θ
R
For steady speed, F
net
= F
m
− F
g
= 0
∴
v B
2
l
2
cos
2
θ
R
− mg sin θ = 0
or v =
mg R sin θ
B
2
l
2
cos
2
θ
13.76 ξ = π R
2
Bf
∴ B =
ξ
π R
2
f
=
6.28 × 10
−3
3.14 × (0.1)
2
(1200/60)
= 0.01 T
13.77
[emf]=[electric field][distance]
=[force/charge][distance]
=[MLT
−2
Q
−1
][L]=[ML
2
T
−2
Q
−1
]
[dφ
B
/dt]=[φ
B
][T
−1
]=[B][area][T
−1
]
=[force/(velocity) charge][L
2
][T
−1
]
=[MLT
−2
/LT
−1
Q][L
2
][T
−1
]

13.3 Solutions 627
=[ML
2
T
−2
Q
−1
]
∴ [emf]=[dφ
B
/dt]
13.78 The flux through the coil
φ = B · A = 15 ×10
−4
× 3 × 10
−12
sin(4 × 10
6
t)
ξ =−N
dφ
dt
=−200 × 15 × 10
−4
× 3 × 4 × 10
6
× 10
−12
cos(4 × 10
6
t)
=−3.6 × 10
−6
cos(4 × 10
6
t) V
13.79 ξ ∝
dφ
dt
or ∝
dB
dt
B = B
0
sin(ωt +φ)
∴ ξ ∝ ωB
0
cos(ωt +φ)
∴
ξ
max
(television)
ξ
max
(radio)
=
ω
1
ω
2
=
f
1
f
2
=
100
1
= 100
∵ B
0
is the same for both the waves.
13.80 The flux φ
B
enclosed by a loop of area A is given by φ
B
= BA, where B
is the magnetic field. Faraday’s law of induction says that the induced emf ξ
is a circuit equal to the negative rate at which the flux through the circuit is
changing. In symbols ξ =−dφ
B
/dt, the current being I = ξ/R, where R is
the resistance. The magnetic force on a straight wire is given by F = il ×B:
φ
B
= BA = Blx (B⊥l)
By Faraday’s law
ξ =−
dϕ
B
dt
=−
d
dt
(Blx) =−Bl
dx
dt
= Blv
i =
ξ
R
=
Blv
R
∴ Force F = ilB =
B
2
l
2
v
R
If the magnetic force acts as a resisting force then equation of motion will be
ma =−
B
2
l
2
v
R
or m
dv
dt
= m
dv
ds
ds
dt
= mv
dv
ds
=−
B
2
l
2
v
R
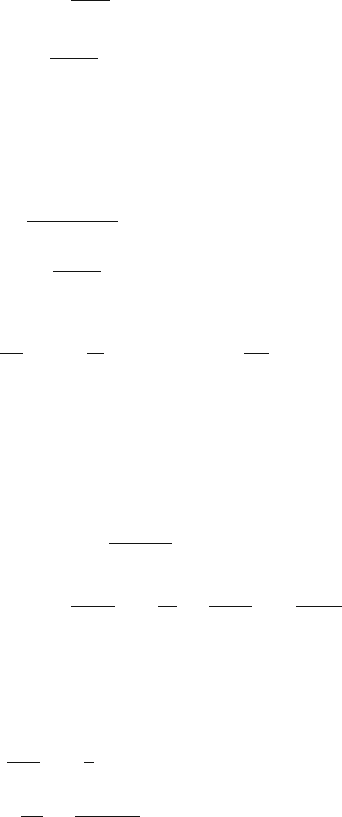
628 13 Electromagnetism I
∴ dv =−
B
2
l
2
mR
ds
v =
dv =−
B
2
l
2
s
mR
+ C
where C = constant of integration.
When s = 0, v = u
∴ c = u
∴ s =
(u − v)mR
B
2
l
2
∴ s
max
=
umR
B
2
l
2
where we have put v = 0.
13.81
ξ =−N
dφ
dt
=−N
d
dt
(BA) =−Nπr
2
dB
dt
(Faraday’s law)
=−100 × π(0.1)
2
(0.1) = 0.314 V
13.82
(i) The flux on one side is equal and opposite to that on the other for 0 <
r < b−x, where r is the distance of any point from the long wire. Only
the flux through the portion b − x < r < x is not cancelled:
dφ = (adr)db =
μ
0
Iadr
2π r
∴ φ =
μ
0
Ia
2π
x
b−x
dr
r
=
μ
0
Ia
2π
ln
x
b − x
(ii) φ →∞for x → b and φ = 0forx = b/2
(iii) For I = 2t and x = b/4
φ =
μ
0
a
2π
ln
1
3
2t
ξ =−
dφ
dt
=
μ
0
a ln 3
π
13.83 Betatron is a machine to accelerate electrons to high energy. It consists of
an evacuated ‘doughnut’ in which the electrons are made to circulate under
the influence of changing magnetic field. If a magnetic flux φ changes in an
electromagnet, it accelerates the electrons and at the same time holds them
in an orbit of fixed radius. The average force acting on the particle during a
single rotation is the work (induced voltage multiplied by charge) divided by
the distance 2π R. Equating this to the time rate of change of momentum, by
Faraday’s law of induction

13.3 Solutions 629
e
dφ
dt
= 2π R
dP
dt
e
dφ/dt
2π R
=
dp
dt
=
d
dt
(BeR)
where B is the magnetic field and R is the radius.
Integrating and assuming that initially the flux is zero and R is constant
φ = 2π R
2
B
13.3.6 Hall Effect
13.84 Consider a strip of a conductor of width W and thickness t carrying a d.c
current i in the positive x-direction along its length, Fig. 13.32. A magnetic
field B setupinthez-direction into the page produces a deflection force in
the positive y-direction, as the drift velocity of electrons is in the negative
x-direction. Consequently charge concentration builds up towards the upper
edge of the strip. As the charges collect on one side of the strip they set up
an electric field that opposes sideways motion of additional charge carriers
inside the conductor. This build up of charges establishes a potential V
H
across the width of the strip, called Hall potential and the phenomenon is
known as Hall effect. Eventually equilibrium conditions are reached and a
maximum voltage, known as Hall voltage, is quickly established. The sign
of the voltage gives the sign of charge carriers and its magnitude the number
density n of charge carriers:
Fig. 13.32 Hall effect
(a)
E
H
= v
d
B =
iB
ne
=
iB
newb
=
100 × 10
1.25 × 10
30
× 1.6 × 10
−19
× 10
−3
× 0.02
= 2.5 ×10
−4
V/m
The field is along positive y-direction.
(b) When equilibrium is established the Lorentz force is zero:
