Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.


610 13 Electromagnetism I
(b) In the limit n →∞,tan
π
n
→
π
n
and (5) becomes
B =
μ
0
i
2a
an expression which is identical for B for a circular loop. This is reason-
able since as n →∞, polygon → circle.
13.29 For square l = 4a and for circle l = 2πr
∴
a
r
=
π
2
(1)
At the centre of the circle, B
c
=
μ
0
i
2r
.
At the centre of the square, B
s
=
2
√
2 μ
0
i
πa
via prob. (13.24).
∴
B
c
B
s
=
π
4
√
2
a
r
=
π
2
8
√
2
= 0.87
13.30
(a) The magnetic induction B at the centre of a circular wire is B =
μ
0
i
2r
.
Hence for the arc which subtends an angle θ at the centre
B =
μ
0
i
2r
θ
2π
=
μ
0
i θ
4π r
Induction at C due to the inner arc is
B
1
=
μ
0
iθ
4 π R
1
and due to the outer arc
B
2
=−
μ
0
iθ
4 π R
2
The negative sign arises due to the fact that the current has reversed. As
the radial part of the path points towards C, it does not contribute to B.
Therefore, the resultant induction is
B = B
1
+ B
2
=
μ
0
iθ
4π
1
R
1
−
1
R
2
Note that for clockwise current we take B as positive and for counter-
clockwise we take B as negative.

13.3 Solutions 611
(b) Put θ = π to obtain
B =
μ
0
i
4
1
R
1
−
1
R
2
13.31 The total induction is given by adding B
s
due to the straight conductor which
contributes on both sides of P and B
c
due to the circular path, both being
directed out of page (Fig. 13.9)
B
s
=
μ
0
i
2 π R
B
c
=
μ
0
i
2R
B = B
s
+ B
c
=
μ
0
i
2π R
(π +1)
13.32
dB =
μ
0
i
4π
d s × r
r
3
(Biot–Savart law) (1)
The magnetic induction dB atPonthez-axis due to an element of length dl of
the ring is shown in Fig. 13.26. Resolving dB along z-axis and perpendicular
to it, and summing over all such elements it is seen that the perpendicular
components vanish for reasons of symmetry and the parallel components get
added up.
Writing dl for ds and noting that the angle between R and dl is 90
◦
, (1) can
be written as
dB
z
= (dB) cos α =
(μ
0
irdl) cos α
4πr
3
(2)
Writing dl = Rdφ, where φ is the azimuth angle and r cos α = R,(2)
becomes
Fig. 13.26 Magnetic
induction on the axis of a
current-carrying ring

612 13 Electromagnetism I
dB
z
=
μ
0
iR
2
dφ
4π r
3
(3)
Integrating
B
z
= B =
dB
z
=
μ
0
iR
2
4π r
3
2π
0
dφ =
μ
0
iR
2
2 (R
2
+ z
2
)
3/2
(4)
13.33 B =
μ
0
Ni
l
=
4π ×10
−7
× 500 × 5
1.0
= 3.14 ×10
−3
T
13.34 B =
μ
0
I
2π
1
x
+
1
d − x
13.35 Apply Ampere’s law inside the hollow cylindrical conductor
(B)(2π r) =
μ
0
i π(r
2
− a
2
)
π(b
2
− a
2
)
(1)
where the right-hand side includes only the fraction of the current that passes
through the surface enclosed by the path of integration. Solving for B,
B =
μ
0
i
2 π r
(r
2
− a
2
)
(b
2
− a
2
)
.
13.36 Magnetic field at P, due to loop A is
B
A
=
μ
0
INR
2
2(R
2
+ x
2
)
3/2
(1)
where x = AP =
R
2
. Similarly the magnetic field B
c
due to the second loop
is given by an identical expression with x = CP =
R
2
. As the currents are in
the opposite direction these two fields are added:
∴ B = B
A
+ B
C
=
μ
0
INR
2
(R
2
+ x
2
)
3/2
(2)
Put x = R/2 to find
B =
8 Nμ
0
I
5
3/2
R
(3)
13.37 Consider a ring of radius r, width dr, concentric with the disc. The charge
on the ring, Fig. 13.27
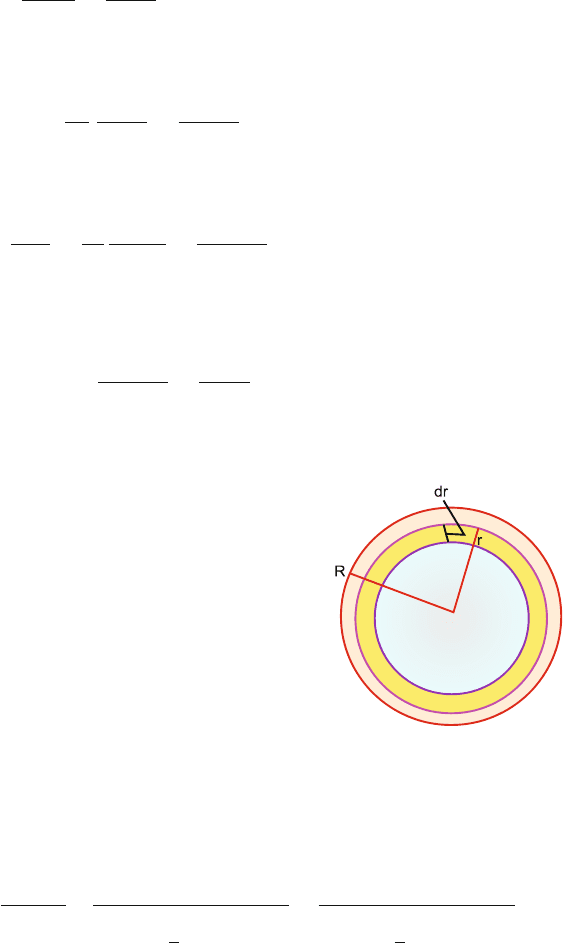
13.3 Solutions 613
dq = q
2πrdr
π R
2
=
2qr dr
R
2
(1)
The elementary current due to rotation of charge with frequency f is
di = f dq =
ω
2π
2qr dr
R
2
=
ω qr dr
π R
2
(2)
The induction at the centre due to the current in the ring is
dB =
μ
0
di
2r
=
μ
0
2r
ω qr dr
π R
2
=
μ
0
ω qdr
2π R
2
(3)
Total induction from the rotating disc
B =
dB =
R
0
μ
0
ω qdr
2 π R
2
=
μ
0
ω q
2 π R
(4)
Fig. 13.27 Magnetic
induction at the centre of a
charged rotating disc
13.38 The field at any point P
1
at distance x from P, the middle point will be
B =
μ
0
iNR
2
2
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
1
R
2
+
1
2
R + x
2
!
3/2
+
1
R
2
+
1
2
R − x
2
!
3/2
⎫
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎭
(1)
by prob. (13.36).

614 13 Electromagnetism I
Differentiate B with respect to x and evaluate
∂ B
∂x
x =0
to find the first
derivative zero. Differentiate B once again to find
∂
2
B
∂x
2
x =0
= 0. Thus
the field around P is seen to be fairly uniform.
13.39
(i)
B =
μ
0
i
2π r
(r > R) (1)
=
4π ×10
−7
× 100
2π ×1.0
= 2 ×10
−5
T
(ii)
B =
μ
0
ir
2π R
2
(r < R) (2)
=
4π ×10
−7
× 100 × 6 × 10
−3
2π ×(3 × 10
−2
)
2
= 1.33 ×10
−6
T
13.40
(a)
B
t
l = μ
0
i (Ampere’s law)
Bl = Bl = B · 2π r = μ
0
i
where we enclose the current i by going round once the circle of radius
r. The magnetic induction will be tangential to the circle and the sum-
mation is simply the circumference of the circle, Fig. 13.28a:
(B)(2πr) = μ
0
i
∴ B =
μ
0
i
2πr
(r > R)
(b) Consider a circular path C at distance r < R,Fig.13.28b. The current
i
0
inside a cross-section of radius r is proportional to the cross-sectional
area
i
0
= i
πr
2
π R
2
=
ir
2
R
2
By Ampere’s law
Fig. 13.28 Magnetic
induction due to a
current-carrying cylinder
(a) (b)
13.3 Solutions 615
B
t
l = (B)(2π r) = μ
0
i
0
= μ
0
i
r
2
R
2
∴ B =
μ
0
ir
2π R
2
(r < R)
13.41 Let the radius of the inner arc of the loop be r and that of the outer arc 2r.
Both the arcs are quarter of a circle. The straight portions do not contribute
to B as their directions pass through P. As the currents in the two arcs flow
in the opposite sense, B will be down due to current in the outer arc and up
due to the current in the inner wire:
∴ B
net
=
1
4
μ
0
I
2r
−
1
4
μ
0
I
2 × 2r
=
μ
0
I
16 r
down
13.42 By prob. (13.22) at P, Fig. 13.29
B =
μ
0
I
4π x
(cos θ
1
+ cos θ
2
), (1)
put θ
1
= θ
2
then
cos θ
1
= cos θ
2
=
L/2
(
L/2
)
2
+ x
2
So that (1) becomes
B =
μ
0
I
4π x
L
(
L/2
)
2
+ x
2
(2)
(a) Let the square be of side a = l/4. The distance of the centre of square
from the side is a/2. Put x = a/2 and L = a = l/4 in (2) to find for one
side
B
1
=
2
√
2μ
0
I
πl
As there are four equal sides, B = 4B
1
=
8
√
2μ
0
I
πl
·
The B-field will be perpendicular to the plane containing the wire and
the field point.
(b) Let each side of the equilateral triangle be a = l/3. Distance of the
centre of the triangle from any side is x = a/2
√
3. Put L = a = l/3
and x = a/2
√
3 in (1) to find for one side B
1
=
9μ
0
I
2πl
. Hence for three
sides

616 13 Electromagnetism I
Fig. 13.29 Magnetic field
due to a current-carrying
straight wire of finite length
B = 3B
1
=
27μ
0
I
2πl
∴
B (square)
B (triangle)
=
27/2
8
√
2
= 1.19
13.43 By prob. (13.36) B =
8Nμ
0
I
5
3/2
R
=
(8)(100)(4π ×10
−7
)(2)
5
3/2
(0.2)
9 ×10
−4
T
13.44
B dl = μ
0
i (Ampere’s law)
By prob. (13.43)
B =
μ
0
Ir
2π R
2
(r < R) (1)
∴ For r =
R
2
, B =
μ
0
I
4π R
(2)
Further B =
μ
0
I
2πr
(r > R). (3)
Equating (2) and (3) we find r = 2R. Thus at r = 2R, the magnetic field is
the same as at r = R/2.
13.45 (a) In the absence of magnetic material the number of flux linkages Nφ
B
(N
being the number of turns) is proportional to the current
Nφ
B
= Li (1)
If n is the number of turns per unit length, A the cross-sectional area and
l the length of the solenoid and B the magnetic induction
Nφ
B
= (nl)(BA) (2)
By Ampere’s theorem
B = μ
0
ni (3)
Combining (1), (2) and (3)
L = μ
0
n
2
Al (4)

13.3 Solutions 617
(b)
B = μ
0
ni =
μ
0
Ni
l
U
B
= u
B
Al =
B
2
2μ
0
· Al =
(μ
0
Ni)
2
Al
2μ
0
l
2
=
μ
0
N
2
i
2
πr
2
2l
=
(4π ×10
−7
)(100)
2
(5)
2
π(0.01)
2
2 × 0.1
= 4.93 ×10
−4
J
(c)
φ = BA =
μ
0
Ni
l
· πr
2
=
4π ×10
−7
× 100 × 5 × π × (0.1)
2
0.1
= 1.972 ×10
−4
Wb
ξ =
−φ
t
=
−1.972 × 10
−4
5
=−3.94 × 10
−5
V
13.46 (a) B =
μ
0
i
2πr
=
4π ×10
−7
× 3
2π ×50 × 10
−3
= 1.2 ×10
−7
T
(b) In the vector form the Biot and Savart law can be written as
dB =
μ
0
i
4π
dl × r
r
3
(i) dB =
(4π ×10
−7
)(2)(2
ˆ
k ×3
ˆ
i)
4π 3
3
= 4.44×10
−8
ˆ
j (∵
ˆ
k ×
ˆ
i =
ˆ
j)
Thus dB = 4.44 × 10
−8
T along positive y-axis
(ii) dB =
(4π ×10
−7
)(2)(2
ˆ
k ×(−6
ˆ
i))
4π 6
3
=−1.11 × 10
−8
ˆ
j
Thus dB = 1.11 × 10
−8
T along negative y-axis
(iii) dB = 0 (∵
ˆ
k ×
ˆ
k = 0)
(iv)
dB =
(4π ×10
−7
)(2)(2
ˆ
k ×3
ˆ
j)
4π 3
3
=−4.44 × 10
−8
ˆ
i
dB = 4.44 × 10
−8
T along negative x-axis.
13.47 H = n
0
i =
Ni
2πr
=
100 × 2
2π ×0.1
= 318.47 A/m for both vacuum and material.
B = K μ
0
H = 1 × 4π ×10
−7
× 318.47 = 4 × 10
−4
T (vacuum)
B = 500 ×4π ×10
−7
× 318.47 = 0.2 T (material)
M =
B −μ
0
H
μ
0
= 0 (vacuum)
M =
B
μ
0
− H =
0.2
4π ×10
−7
− 318 = 1.59 × 10
5
(material)
13.48 Use the formula for B(z) on the axis of a circular coil of radius r carrying
current i:

618 13 Electromagnetism I
B(z) =
μ
0
ir
2
2(r
2
+ z
2
)
3/2
(1)
Use the following values:
B = 6 × 10
−5
T, μ
0
= 4π × 10
−7
A/m, r = 10
6
m and z = 6.4 × 10
6
m
(distance of the pole from earth’s centre) and solve for the current i. We find
i = 2.6 ×10
10
A. Thus the order of magnitude of current is 10
10
A.
13.49 The induction midway between Helmholtz coils is (prob. 13.36)
B =
8N μ
0
I
5
3/2
R
(1)
Given N = 50, I = 10 A, R = 0.5 m and μ
0
= 4π × 10
−7
H/m
∴ B = 8.94 × 10
−4
T(2)
Emf generated between the centre and the rim of the disc is
ξ = πr
2
Bf = π ×(0.1)
2
×8.94×10
−4
×16.66 = 468×10
−6
V = 468 μ V.
13.50 Given
l = 1.0m,v= 3
ˆ
i +2
ˆ
j +3
ˆ
k, B =
ˆ
i +2
ˆ
j +3
ˆ
k
Voltage developed
ξ =
|
v × B
|
l sin φ =
|
v
||
B
|
(sin θ)l sin φ
where θ is the angle between v and B, φ is the angle which l makes with B:
|
v
|
=
3
2
+ 2
2
+ 1
2
1/2
=
√
14
|
B
|
=
1
2
+ 2
2
+ 3
2
1/2
=
√
14
cos θ =
v · B
|
v
||
B
|
=
3 + 4 + 3
√
14
√
14
=
5
7
∴ sin θ = 0.4898
∴ ξ =
√
14
√
14
(
0.4898
)
(1) sin φ = 6.857 sin φ
ξ will be maximum for φ = 90
◦
and zero for φ = 0 or 180
◦
.
13.51 The motion of the proton is equivalent to a current. The current density is
given by

13.3 Solutions 619
J = ev (1)
The magnetic field due to a current-carrying circuit is given by the Biot–
Savart law
dB =
μ
0
I
4π
dl
× R
R
3
(2)
When dl
is the circuit element, R is the vector which points from dl
to the
field point. As there is only one proton there is no need to integrate to find
B. Replacing the current by the current density J, the Biot–Savart law is
modified as
B =
μ
0
4π
J × R
R
3
(3)
Substituting (1) into (3)
B =
μ
0
e
4π
v × R
R
3
R =
ˆ
i +2
ˆ
j
m
v =
ˆ
i +3
ˆ
j
10
4
m/s
v × R = 10
4
ˆ
i
ˆ
j
ˆ
k
130
120
=−10
4
ˆ
k
B =
4π ×10
−7
4π
× 1.6 × 10
−19
×
−10
4
ˆ
k
√
5
3
= 1.43 ×10
−23
ˆ
k T
13.3.3 Magnetic Force
13.52
F
l
=
μ
0
i
1
i
2
2π d
=
4π ×10
−7
× 2 × 3
2π ×0.05
= 2.4 ×10
−5
N
13.53
F
l
=
μ
0
i
1
i
2
2 π d
∴ i
2
=
2πd
μ
0
i
1
F
l
=
2π ×0.2 × 10
−5
4π ×10
−7
× 10
= 1.0A
The currents are parallel.
