Kamal A.A. 1000 Solved Problems in Classical Physics: An Exercise Book
Подождите немного. Документ загружается.

660 14 Electromagnetism II
f
0
=
1
2π
√
LC
=
1
2π
√
0.2 × 10 × 10
−6
= 112.6Hz
14.22
X
C
=
1
2π fC
=
1
(2π)(300)(50 × 10
−6
)
= 10.6
Z =
R
2
+ X
2
C
=
(300)
2
+ (10.6)
2
= 300.19
I =
V
Z
=
5
300.19
= 0.0166 A
14.23 Impedance of a capacitor
i. Let an AC emf be applied across a capacitor. The potential difference
across the capacitor will be
V
C
= V
0
sin ωt (1)
where V
0
is the amplitude of the AC voltage of angular frequency ωt =
2π f , across the capacitor.
q
C
= CV
C
= CV
0
sin ωt (2)
The current i
c
=
dq
C
dt
= ωCV
0
cos ωt = ωCV
0
sin(ωt +90
◦
) (3)
or i
c
=
V
0
X
c
sin (ωt +90
◦
) (4)
where X
C
= 1/ωC (5)
Comparison of (4) with (1) shows that i
c
leads V
C
by 90
◦
or quarter of a
cycle. Further, the current amplitude
I
0
=
V
0
X
C
(6)
By Ohm’s law X
C
is to be regarded as impedance offered by the capaci-
tor. In complex plane
Z
c
=
−j
ωC
(7)
where j is imaginary.
Impedance of an inductance
On applying an AC across an inductance the potential difference will be
V
L
= V
0
sin ωt (8)
where V
0
is the amplitude of V
L
. By Faraday’s law of induction (ξ =
−L di/dt) we can write

14.3 Solutions 661
V
L
= L
di
L
dt
(9)
Combining (8) and (9)
di
L
dt
=
V
0
L
sin ωt (10)
∴ i
L
=
di
L
=
V
0
L
sin ωt dt =−
V
0
ωL
cos ωt
∴ i
L
=
V
0
X
L
sin(ωt −90
◦
) (11)
where X
L
= ωL (12)
is known as the inductive impedance. In complex plane X
L
= jωL,
where j is imaginary. Comparison of (11) with (8) shows that the current
in the inductance lags behind the voltage by 90
◦
or quarter of a cycle.
ii. Z
L
=
√
R
2
+ ω
2
L
2
=
(44)
2
+ (2π ×150 × 0.06)
2
= 71.63
Z
C
=
R
2
+
1
ω
2
C
2
=
10
2
+
1
(2π ×150 × 10
−4
)
2
= 14.58
14.24
(a) Electric current is the time rate of flow of charge; in symbols I = dQ/dt.
(b) The charge Q is an integral multiple of the unit of electron’s charge
e, that is, Q = ne, where n is a number. The charge Q is said to be
quantized
(c) (i) Current density j =
i
A
=
2.4 × 10
−4
(5.6 × 10
−3
)(50 × 10
−6
)
= 857 A/m
2
(ii) Drift speed V
d
=
j
ne
=
857
(8.5 × 10
28
)(1.6 × 10
−19
)
= 6.3 ×
10
−8
m/s
(iii) Collisions with atoms and ions of the conductor makes possible
large currents to pass.
14.25
By problem ω =
1
√
L
1
C
1
=
1
√
L
2
C
2
(1)
When the combinations L
1
C
1
and L
2
C
2
are connected in series, the combi-
nation will have inductance L and capacitance C given by
L = L
1
+ L
2
(2)
C =
C
1
C
2
C
1
+ C
2
(3)
Now LC =
(
L
1
+ L
2
)
C
1
C
2
C
1
+C
2
(4)
662 14 Electromagnetism II
From (1) we have L
2
=
L
1
C
1
C
2
(5)
Substituting (5) in (4) we get on simplification LC = L
1
C
1
=
1
ω
2
It follows that ω =
1
√
LC
14.26
Z
c
=
1
ωc
=
1
2πfc
∴ C =
1
2πfz
c
=
1
2π ×1000 × 500
= 3.18 ×10
−7
F = 0.318 μF
Z
L
= ωL = 2πfL
∴ L =
Z
L
2π f
=
100
2π ×5000
= 3.18 ×10
−3
H = 3.18 mH
14.27 The maximum stored energy in the capacitor must equal the maximum stored
energy in the inductor, from the principle of energy conservation.
∴
1
2
q
2
m
C
=
1
2
Li
2
m
(1)
where i
m
is the maximum current and q
m
is the maximum charge. Substitut-
ing CV
0
for q
m
and solving for i
m
in (1)
i
m
= V
0
C
L
= 100
0.01 × 10
−6
10 × 10
−3
= 0.1A
14.28 For resonance
ω =
1
√
LC
∴ C =
1
4π
2
f
2
L
=
1
4π
2
(5 × 10
5
)
2
× 10
−3
= 1.013 ×10
−9
F
Quality factor
Q =
ωL
R
∴ R =
2πfL
Q
=
2π(500 × 10
3
)(10
−3
)
150
= 20.944
∴ Resistance to be included in series is 20.944 − 5.0 = 15.944 .
14.3 Solutions 663
14.29 For parallel resonance circuit
ω = ω
0
1 −
CR
2
L
ω
0
=
1
√
LC
=
1
√
10
−3
× 5 × 10
−6
= 1.414214 ×10
6
rad/s
f =
ω
2π
=
ω
0
2π
1 −
CR
2
L
=
1.414214 × 10
6
2π
1 −
5 × 10
−10
× 10
2
10
−3
= 2.250736 ×10
5
/s
Quality factor
Q =
ωL
R
=
1.414 × 10
6
× 10
−3
10
= 141.4
14.30
V = V
0
e
−t/RC
ln V = ln V
0
−
t
RC
V
V
= 0 −
t
C
d
dR
1
R
R −
t
R
d
dC
1
C
C
=
t
CR
R
R
+
C
C
=
50 × 10
−6
10
−8
× 5 × 10
4
5
100
+
10
100
= 0.015
14.31
(a) V = ξ e
−t/RC
The voltage on the condensor will fall to l/e of its initial value when the
time
t = RC = 10
4
× 10
−5
= 0.1s
(b) Error on t will result from error on R.
t = CR
∴ t/t = R/R
Power P = i
2
R =
ξ
2
e
2
R
=
(3000)
2
(2.718)
2
× 10
4
= 121.8W
Energy U = P.t = 121.8 ×0.1 = 12.18 J
Heat H = 12.18/4.18 = 2.914 cal
664 14 Electromagnetism II
Rise in temperature
T = Heat / thermal capacity = 2.914/0.9 = 3.24
◦
C
R = R
0
(1 + αT ) = 10
4
(1 + 0.004 × 3.24)
= 1.01296 ×10
4
R = R − R
0
= 129.6
∴
t
t
=
R
R
0
=
129.6
10
4
= 0.01296
Percentage error =
t
t
× 100 = 1.3%
14.32 The amplitude i
m
of the current oscillations is given by
i
m
=
E
m
(ω
L − 1/ω
c)
2
+ R
2
At resonance, ω
= ω and i
m
=
E
m
R
Set i
m
=
E
m
(ωL − 1/ωc)
2
+ R
2
=
1
2
E
m
R
Squaring and simplifying
ωL −
1
ωc
2
= 3 R
2
or ω
2
LC ±
√
3ωRC − 1 = 0
The only acceptable solutions are
ω
1
=
√
3
2
R
L
+
3R
2
4L
2
+
1
LC
ω
2
=−
√
3
2
R
L
+
3R
2
4L
2
+
1
LC
Subtracting the last equation from the previous one
ω = ω
1
− ω
2
=
√
3
R
L
∴
ω
ω
=
√
3
ω
R
L
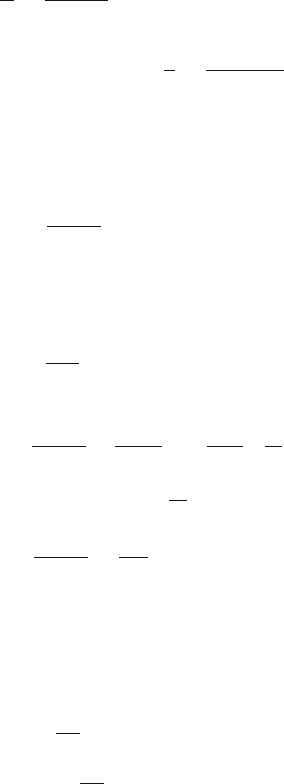
14.3 Solutions 665
14.3.2 Maxwell’s Equations and Electromagnetic Waves,
Poynting Vector
14.33
E
z
= 100 cos(6 × 10
8
t + 4x) (by problem) (1)
E
z
= A cos(ωt + kx) (standard equation) (2)
Comparison of (1) and (2) shows that
ω = 6 ×10
8
and k = 4
v =
ω
k
=
6 × 10
8
4
= 1.5 ×10
8
m/s
Dielectric constant, K =
c
v
=
3 × 10
8
1.5 × 10
8
= 2.0
14.34
E · ds = q/ε
0
(Gauss’ law)
E(2π rl) = q/ε
0
∴ E =
λˆe
r
2πr ε
0
(1)
B · ds = μ
0
I (Ampere’s law)
2πrB = μ
0
I
∴ B =
μ
0
I
2πr
ˆe
φ
(2)
E
r
= γ(E
r
− v B
φ
) (Lorentz transformation) (3)
= γ
λ
2πr ε
0
−
vμ
0
I
2πr
=
γ
2π r
λ
ε
0
− vμ
0
I
Thus E
r
= 0ifvμ
0
I =
λ
ε
0
or v =
λ
Iμ
0
ε
0
=
λc
2
I
14.35 Maxwell’s equations in vacuum are
∇·E = 0(1)
∇·B = 0(2)
∇×E =−
∂B
∂t
(3)
∇×B = μ
0
ε
0
∂E
∂t
(4)
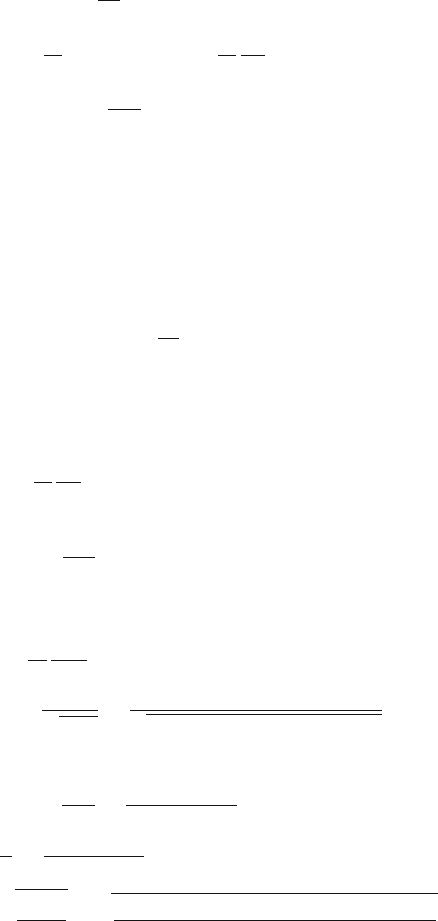
666 14 Electromagnetism II
Use the vector identify
∇ × (∇ × B) = ∇(∇ · B) −∇
2
B
∴ ∇×
μ
0
ε
0
∂E
∂t
=−∇
2
B (∵ ∇ · B = 0by(2)
∴ μ
0
ε
0
∂
∂t
(∇ × E) =−μ
0
ε
0
∂
∂t
∂B
∂t
=−∇
2
B
∴ ∇
2
B = μ
0
ε
0
∂
2
B
∂t
2
14.36
∇ × B = μ
0
j (Ampere’s law) (1)
Use the vector identity A ·(A ×B) = 0. Put A = ∇.
∴ ∇ · (∇ ×B) = 0
∴ ∇ · j = 0(2)
More generally, ∇ · j +
∂ρ
∂t
= 0 (continuity equation) (3)
and ∇ · E = ε
0
ρ (Gauss’ law) (4)
Combining (3) and (4)
∇ ·
j +
1
ε
0
∂E
∂t
= 0
14.37 ∇
2
B = μ
0
ε
0
∂
2
B
∂t
2
(free-space wave equation)
Compare with the standard three-dimensional wave equation
∇
2
=
1
v
2
∂
2
∂t
2
(5)
∴ v =
1
√
μ
0
ε
0
=
1
(4π ×10
−7
)(8.854 × 10
−12
)
= 2.998 ×10
8
m/s = c
14.38
ω = 2πν =
2πc
λ
=
2π ×3 × 10
8
530 × 10
−9
= 3.55 ×10
15
σ =
1
ρ
=
1
26.5 × 10
−9
= 3.77 ×10
7
δ =
2
μ
0
σω
=
2
4π ×10
−7
× 3.77 × 10
7
× 3.55 × 10
15
= 3.45 ×10
−9
m = 3.45 nm
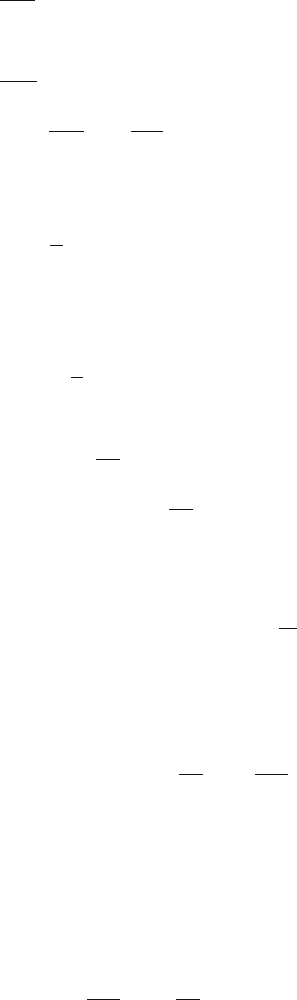
14.3 Solutions 667
14.39
E = E
0
cos(kx − ωt) (1)
∂ E
y
∂x
=−kE
0
sin(kx − ωt) (2)
B = B
0
cos(kx − ωt) (3)
∂ B
Z
∂t
= ω B
0
sin(kx − ωt) (4)
But
∂ E
y
∂x
=−
∂ E
z
∂t
(5)
Combining (2), (4) and (5), we get
E
0
=
ω
k
B
0
= cB
0
14.40 Maxwell’s equations for a non-ferromagnetic homogeneous isotropic
medium can be written as
∇ · E =
ρ
ε
(1)
∇ · B = 0(2)
∇ × E =−
∂B
∂t
(3)
∇ × B = μσ E + με
∂E
∂t
(4)
Taking the curl of (4)
∇ × (∇ × B) = μσ (∇ ×E) + με
∂
∂t
(∇ × E) (5)
where the time and space derivatives are interchanged as E isassumedtobe
a well-behaved function. Expression (3) can be substituted in (5) to obtain
∇ × (∇ × B) =−μσ
∂B
∂t
− με
∂
2
B
∂t
2
(6)
Using the vector identity
∇ × (∇ × B) = ∇ (∇ ·B) −∇
2
B (7)
By virtue of (2), ∇ · B = 0 and (6) becomes
∇
2
B = με
∂
2
B
∂t
2
+ μσ
∂B
∂t
(8)
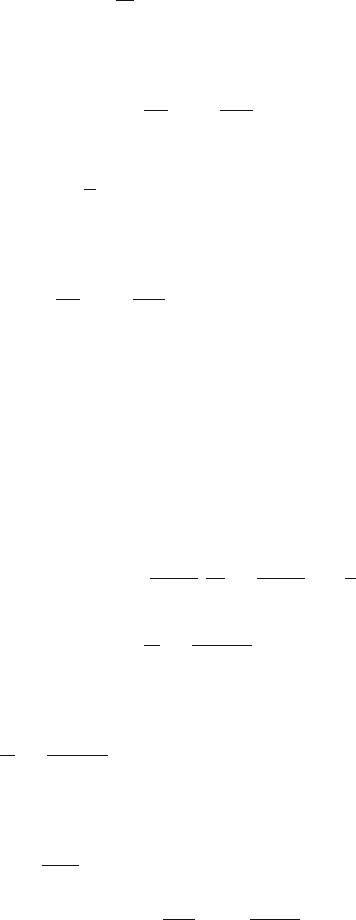
668 14 Electromagnetism II
A similar procedure applied to (3) yields a similar equation for the E-field.
Taking the curl of (3)
∇ × (∇×E) =−
∂
∂t
(∇×B) (9)
Using (4) in (9)
∇ × (∇ × E) =−μσ
∂E
∂t
− με
∂
2
E
∂t
2
(10)
But ∇ × (∇ × E) = ∇(∇ · E) −∇
2
E (11)
and ∇ · B =
ρ
ε
(1)
Combining (10), (11) and (1) we obtain for uncharged medium (ρ = 0)
∇
2
E = μσ
∂E
∂t
+ με
∂
2
E
∂t
2
14.41
(a)
ε
0
E · dS = q (Gauss’ law) (1)
ε
0
E(2πrl) = q
or E = q/2πε
0
rl (2)
the flux being entirely through the cylindrical surface and zero through the
end caps. The potential difference between the conductors is
V =
b
a
Edr =
b
a
q
2πε
0
l
dr
r
=
q
2πε
0
l
ln
b
a
Capacitance C =
q
V
=
2πε
0
l
ln(b/a)
(3)
∴ Capacitance per unit length of the cable is
C
l
=
2πε
0
ln(b/a)
(3a)
(b) The magnetic induction between the conductors is
B =
μ
0
i
2π r
(4)
Energy density u =
1
2μ
0
B
2
=
μ
0
i
2
8π
2
r
2
(5)
where we have used (4).
14.3 Solutions 669
Consider a volume element dV for the cylindrical shell of radii r and
r +dr and of length l. The energy contained in the volume element is
dU = u dV =
μ
0
i
2
8π
2
r
2
(2πrl dr) =
μ
0
i
2
l
4π
dr
r
(6)
U =
dU =
μ
0
i
2
l
4π
b
a
dr
r
=
μ
0
i
2
l
4π
ln(b/a) (7)
But U =
1
2
Li
2
(8)
Comparing (7) and (8)
L =
μ
0
l
2π
ln(b/a)
∴ Inductance per unit length of the cable is
L
l
=
μ
0
2π
ln(b/a)
14.42
(a) By prob. (14.41) the potential difference between the conductors is
V =
q
2πε
0
l
ln(b/a) =
λ
2πε
0
ln(b/a) (1)
where λ = q/l is the charge density.
Now E =
λ
2πε
0
r
=
ξ
r ln(b/a)
(2)
where we have put V = ξ .
(b)
B =
μ
0
i
2πr
=
μ
0
ξ
2π rR
(a < r < b) (3)
(c) The Poynting vector
S =
1
μ
0
E × B =
1
μ
0
EB =
ξ
2
2πr
2
R ln(b/a)
where we have used (2) and (3).
14.43
u
B
=
1
2
B · H (1)
B = μ H (2)
