J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

74 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

0.08

−14.29

G(s)

˙ϕ

soll

KurswinkelRuderwinkel

Gierrate

P-Regler

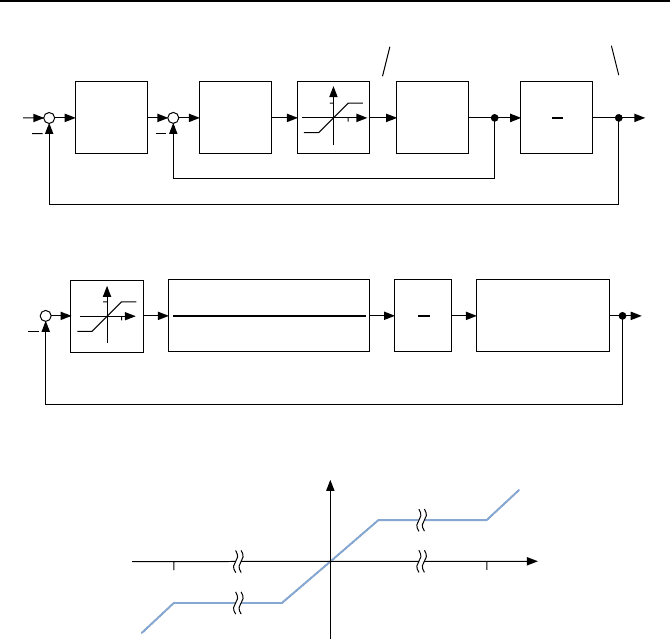
Bild 2.31: Kursregelung der Tampa.

0.0184(s+0.0068)

(s+0.2647)(s+0.0063)

14.29(s +0.08)

˙ϕ

Bild 2.32: Regelkreis des Schiﬀes in Form eines nichtlinearen Standardregelkreises.

−e

Bild 2.33: Modiﬁzierte S

attigungskennlinie.

nicht im Sektor [ε, K > 1], und das Popov-Kriterium ist deshalb eigentlich

nicht anwendbar.

Um es doch anwenden zu k

onnen, verwenden wir den folgenden Kunstgriﬀ.

Es ist zu ber

ucksichtigen, dass keine beliebig großen Werte von e in einem

praktisch betriebenen Regelkreis auftreten. Daher kann die S

attigungskenn-

linie auch ab einem bestimmten Wert e

,oberhalbdessengesichertkeine

Werte mehr im praktischen Betrieb auftauchen, wieder ansteigen. Auf das

Regelkreisverhalten hat diese ge

anderte Kennlinie, Bild 2.33 zeigt sie, keine

Auswirkung. Durch diesen Kunstgriﬀ liegt die Kennlinie im Sektor [ε, K > 1]

und die Stabilit

at l

asst sich dann doch sicherstellen.

Zu erw

ahnen ist noch, dass eine F

uhrungsgr

oße ϕ

soll

= 0 die Anwendung

des Popov-Kriteriums nicht beeintr

achtigt. Denn die negierte F

uhrungsgr

oße

−ϕ

soll

kann auch als Anfangswert ϕ(0) des Kurswinkels interpretiert werden.

Die zugeh

orige Popov-Ortskurve des Regelkreises zeigt Bild 2.34. Ersicht-

lich kann eine Gerade von links so an die Popov-Ortskurve geschoben werden,

2.2. Absolute Stabilit

at 75

ϕ in Grad

Re Zeit t in s

ω =0

ω →∞

◦

0.05

-0.05

-0.1

-0.15

-0.2

-0.25

100

-0.4-0.2

0.20.40.6 50 100

150

200 250

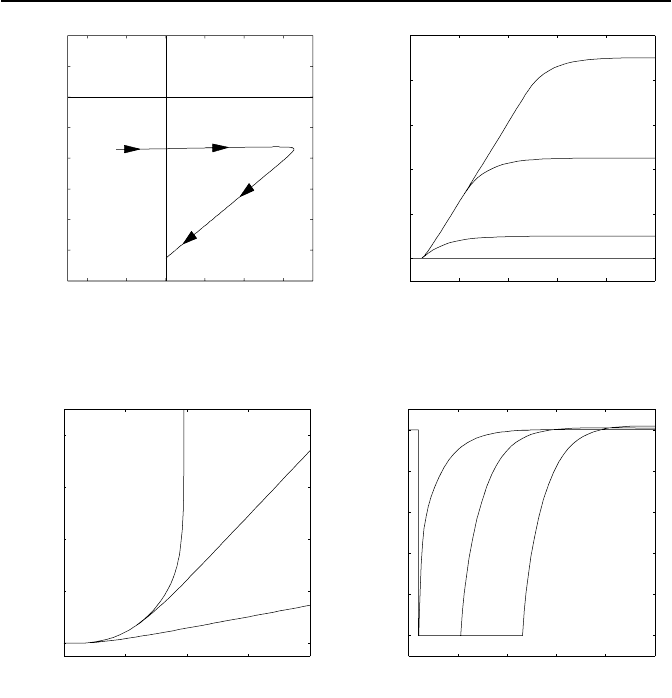
Bild 2.34: Popov-Ortskurve des

Schiﬀes.

Bild 2.35: Kurswinkel ϕ.

y in m

ϑ in Grad

x in m

Zeit t in s

◦

1600

1200

800

400

-2

-4

-6

-8

-10

500 1000 1500 2000

100 150

200

250

Bild 2.36: Schiﬀskurs in Draufsicht. Bild 2.37: Stellgr

oße Ruder-

winkel ϑ.

dass sie durch den Ursprung l

auft. Das System ist also absolut stabil im Sektor

[ε, ∞).

Die Bilder 2.35, 2.36 und 2.37 zeigen die simulierten Verl

aufe der Kurs-

regelung f

ur eine Kurswinkel

anderung von 10

◦

,45

◦

und von 90

◦

,diebei

t = 10 s beginnt. Dabei wurde eine Geschwindigkeit des Schiﬀes von 10 m s

−1

angenommen. Bild 2.37 illustriert, dass ab einer Kurs

anderung, die mehr als

◦

betr

agt, die Stellgr

oße in die S

attigung geht. Das Schiﬀsruder ist dann

am Anschlag. Aus den Bildern ist auch zu erkennen, dass große Kurswin-

kel

anderungen aufgrund des S

attigungseﬀektes langsamer ausgef

uhrt werden

als kleine. Das ist sinnvoll, denn große Kurven sollten nicht so schnell durch-

fahren werden wie kleine. Bild 2.36 zeigt die gefahrenen Kurven und Kurs-

verl

aufe des Schiﬀes in Draufsicht, d. h. in der xy-Ebene.

76 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

2.2.5 Das Kreiskriterium

Das Kreiskriterium erm

oglicht wie das Popov-Kriterium die Untersuchung

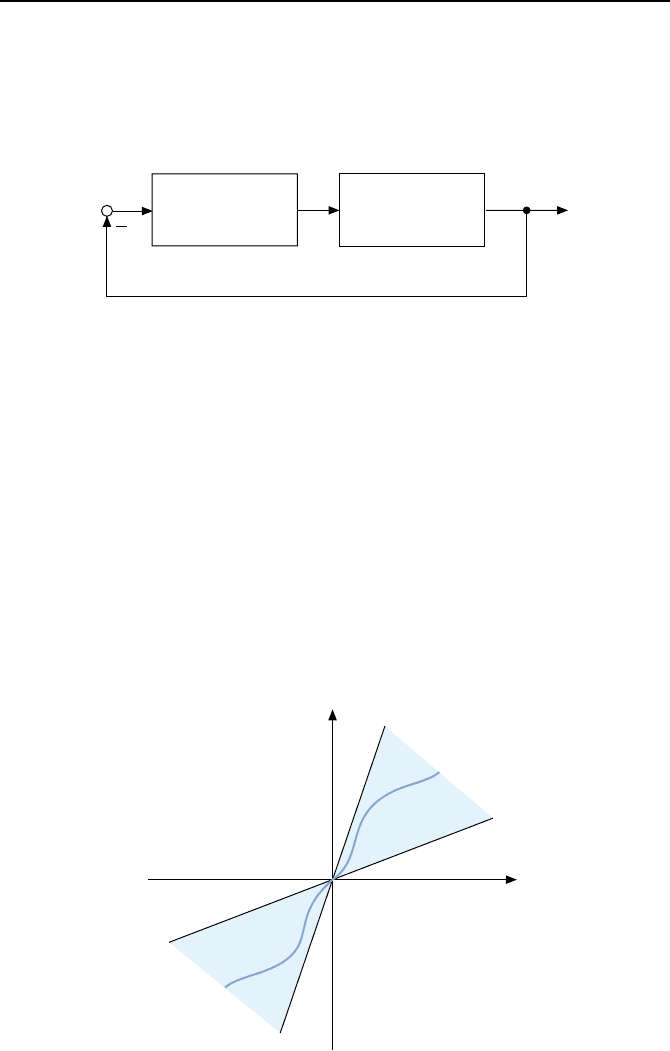
nichtlinearer Standardregelkreise, wie sie Bild 2.38 zeigt, auf absolute Stabi-

lit

at.

u = f(e, t)

G(s)

Bild 2.38: Nichtlinearer Standardregelkreis mit zeitvarianter Kennlinie.

Die nichtlineare Funktion

u = f (e, t)

kann zeitvariant sein und liegt in einem Steigungssektor [K

+ ε, K

− ε]mit

0 ≤ K

< ∞ und beliebig kleinem ε>0, d. h., es gilt

+ ε)e ≤ f (e, t) ≤ (K

− ε)e.

Insbesondere muss also f(0,t)=0erf

ullt sein. Bild 2.39 illustriert die Situa-

tion.

Das Kreiskriterium liefert eine Aussage, ob in einem Sektor [K

+ε, K

−ε]

absolute Stabilit

at f

ur den Standardregelkreis gew

ahrleistet ist. Wie das

f(e)

Bild 2.39: Steigungssektor [K

+ ε, K

− ε] des Kreiskriteriums.

2.2. Absolute Stabilit

at 77

Popov-Kriterium ist das Kreiskriterium allerdings nur hinreichend. Daher wis-

sen wir im Allgemeinen nicht, ob der maximal m

ogliche Sektor absoluter Sta-

bilit

at bestimmt wurde.

Satz 2 (Kreiskriterium). Gegeben sei der nichtlineare Standardregelkreis

Y (s)=G(s)U(s),

e = −y,

u = f(e, t).

Die Kennlinie u = f(e, t) liege im Sektor [K

+ε, K

−ε] mit 0 ≤ K

< ∞

und beliebig kleinem ε>0. Es gelte f(0,t)=0f

ur alle t ∈ IR. Des Weite-

ren sei f zeitinvariant und st

uckweise stetig oder zeitvariant und stetig. Die

Ubertragungsfunktion G(s) sei stabil und ihr Z

ahlergrad m sei kleiner als ihr

Nennergrad n. Wenn unter obigen Voraussetzungen die Ortskurve G(jω) den

Kreis, der in der komplexen Ebene seinen Mittelpunkt auf der reellen Achse

besitzt und durch die Punkte

−

und −

geht, weder umfasst noch schneidet, dann ist der Regelkreis absolut stabil im

Sektor [K

+ ε, K

− ε].

Die Anwendung des Kreiskriteriums ist einfach. Man zeichnet die Ortskur-

ve G(jω) des oﬀenen Regelkreises und den Kreis durch die Punkte −1/K

und

−1/K

, wie es Bild 2.40 zeigt. F

ur alle Kreise und die zugeh

origen Sektoren

+ε, K

−ε], die links der Ortskurve G(jω) liegen, ist der nichtlineare Stan-

dardregelkreis stabil. Oﬀensichtlich erf

ullen viele Kreise diese Bedingung. Der

oßter

oglicher

Kreis

G(jω)

−

Bild 2.40: Anwendung des Kreiskrite-

riums.

Popov-Gerade

G(jω)

Bild 2.41: Vergleich von Popov- und

Kreiskriterium.

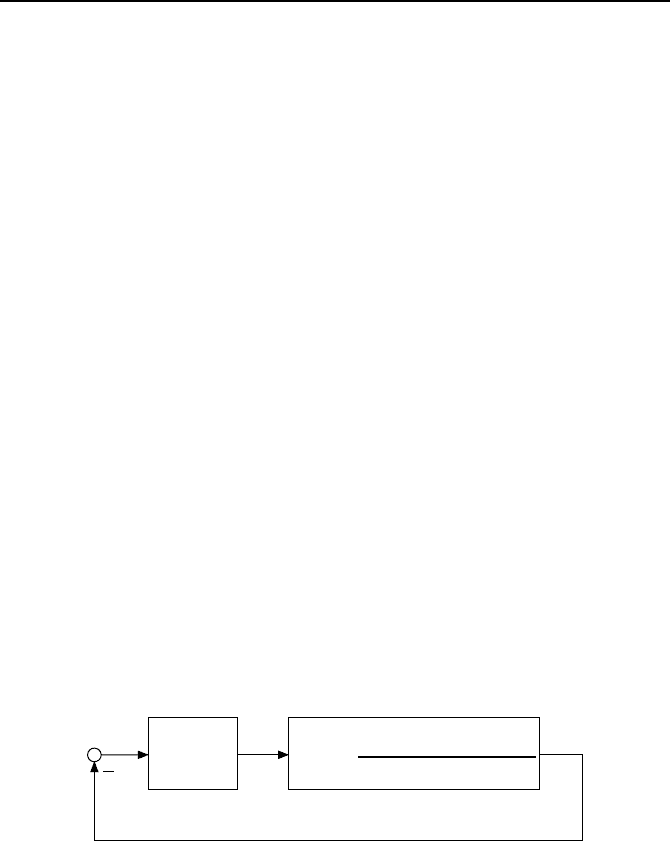
78 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

oßte von ihnen schneidet die reelle Achse in −1/K und hat einen unendlich

großen Durchmesser. Wir erhalten in diesem Fall dann den Sektor [ε, K − ε].

Man beachte, dass der Kreis die Ortskurve zwar nicht schneiden, durchaus

aber tangieren darf.

Im Falle einer instabilen Regelstrecke f

uhrt man die im Abschnitt 2.2.2

schon beim Popov-Kriterium angewandte Sektortransformation durch. So

erh

alt man eine stabile Regelstrecke und das Kreiskriterium ist wieder an-

wendbar.

ur den Grenzfall K

→ K

und ε → 0 entartet der Sektor [K

+ε, K

−ε]

zu einer Geraden, die Kennlinie zur linearen Funktion u = f (e)=K

e und

der Kreis zum Punkt −1/K

. In diesem Fall geht das Kreiskriterium in das

einfache Nyquist-Kriterium

uber.

Das Kreiskriterium ist einfacher in der Anwendung als das Popov-Kriteri-

um, da man nur die meist bereits vorliegende Ortskurve G(jω)ben

otigt und

nicht die Popov-Ortskurve

G(jω). In bestimmten F

allen liefert das Kreiskrite-

rium allerdings einen anderen Sektor absoluter Stabilit

at. Bild 2.41 illustriert

einen solchen Fall. Erg

anzende Informationen ﬁnden sich in [22, 50].

2.2.6 Das Zypkin-Kriterium f

ur zeitdiskrete Systeme

ur den Fall von Abtastregelkreisen mit der Abtastzeit T und der z-

Ubertra-

gungsfunktion G(z) kann der Begriﬀ der absoluten Stabilit

at ganz analog

zum zeitkontinuierlichen Fall deﬁniert werden. Auch hier werden nichtlineare,

statische Kennlinien f betrachtet. Zur Untersuchung der absoluten Stabilit

solcher nichtlinearer zeitdiskreter Regelkreise, wie sie in Bild 2.42 dargestellt

sind, hat Ja. S. Zypkin dem Popov-Kriterium vergleichbare S

atze angegeben

[109, 185, 186, 204].

u = f (e)

G(z)=

+ ...+ b

z + b

+ ...+ a

z + a

Bild 2.42: Nichtlinearer diskreter Standardregelkreis.

Wie sich zeigt, sind diese S

atze dem Popov-Kriterium sehr

ahnlich und

ahnlich einfach anwendbar. Allerdings sind auch die Kriterien von Zypkin,

genau wie das Popov-Kriterium, nur hinreichend. Man kann daher nicht sicher

sein,obmandengr

oßten Sektor absoluter Stabilit

at mittels der Kriterien

ermittelt hat.

Wir betrachten zun

achst ein sehr einfach anwendbares Kriterium von Zyp-

kin.

2.2. Absolute Stabilit

at 79

Satz 3 (Einfaches Zypkin-Kriterium). Gegeben sei der diskrete nichtli-

neare Standardregelkreis

Y (z)=G(z)U (z),

e = −y,

u = f (e)

mit einer Regelstrecke, die h

ochstens einen Pol bei z =1und sonst nur Pole

mit |z| < 1 besitzt. Die Kennlinie u = f(e) sei st

uckweise stetig, eindeutig, f

alle e deﬁniert, gehe durch null und erf

ulle f(e →∞) =0. Dann ist obiger

Regelkreis absolut stabil

(1) im Sektor [0,K],wennG(z) stabil ist,

(2) im Sektor [ε, K] mit einem beliebig kleinen ε>0,wennG(z) h

ochstens

einen Pol in z =1und sonst nur Pole mit |z| < 1 besitzt,

falls die Gleichung

Re {

G(z = e

jωT

)} > −

ur alle 0 ≤ ωT ≤ π erf

ullt ist.

Geometrisch ist das obige Kriterium sehr einfach zu interpretieren. Man

zeichnet die Ortskurve zu G(z = e

jωT

) und schiebt von links in der komplexen

Ebene kommend eine senkrechte Gerade an die Ortskurve heran, bis sie diese

tangiert. Der Schnittpunkt −1/K mit der reellen Achse liefert den gefundenen

Sektor [0,K]bzw.[ε, K] absoluter Stabilit

at. Bild 2.43 illustriert dies.

Der Vorteil dieses Kriteriums ist seine sehr einfache Anwendung. Nachteilig

ist, dass es in manchen F

allen keine gute Absch

atzung des Sektors absoluter

Stabilit

at liefert. Ein erweitertes Kriterium, das eine bessere Absch

atzung

dieses Sektors liefert, ist das Folgende.

Ortskurve G(e

jωT

)

kritische

Zypkin-

Gerade

−

Bild 2.43: Anwendung des einfachen Zypkin-Kriteriums.

80 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Satz 4 (Allgemeines Zypkin-Kriterium). Gegeben sei der diskrete nicht-

lineare Standardregelkreis

Y (z)=G(z)U (z),

e = −y,

u = f (e)

mit der stabilen Regelstrecke G(z). Die Kennlinie u = f (e) sei st

uckweise

stetig, eindeutig, f

ur alle e deﬁniert, gehe durch null und sei monoton. Dann

ist obiger Regelkreis absolut stabil im Sektor [0,K], falls sich eine reelle Zahl

q ≥ 0 ﬁndet, f

ur die die Zypkin-Ungleichung

Re {



1+q(1 − e

−jωT

)



· G(z = e

jωT

)} > −

ur alle 0 ≤ ωT ≤ π erf

ullt ist.

Obiges Kriterium ist analog zu Popovs Kriterium mit dem Unterschied,

dass die Kennlinie u = f(e) monoton sein muss. Dies ist allerdings keine

große Einschr

ankung, da fast alle in der Praxis vorkommenden Kennlinien

diese zus

atzliche Bedingung erf

ullen. Des Weiteren muss q ≥ 0sein.

Das allgemeine Zypkin-Kriterium kann

ahnlich graﬁsch ausgewertet wer-

den wie das Popov-Kriterium. Man formt die Zypkin-Ungleichung

Re {G(e

jωT

)+q(1 − e

−jωT

) · G(e

jωT

)} > −

um zu

Re {G(e

jωT

)}



 

U(ω)

−q



Re {e

−jωT

G(e

jωT

)}−Re {G(e

jωT

)}





 

V (ω)

> −

Wie im Fall des Popov-Kriteriums erh

alt man eine parametrierte Ungleichung:

U(ω) − qV (ω)+

> 0.

Auch hier kann man einen k

unstlichen Frequenzgang bzw. seine Ortskurve,

die Zypkin-Ortskurve

G(e

jωT

)=U(ω)+jV (ω),

deﬁnieren. Verl

auft dann die Zypkin-Ortskurve rechts bzw. unterhalb einer

Geraden mit der Steigung 1/q und dem Schnittpunkt −1/K mit der reellen

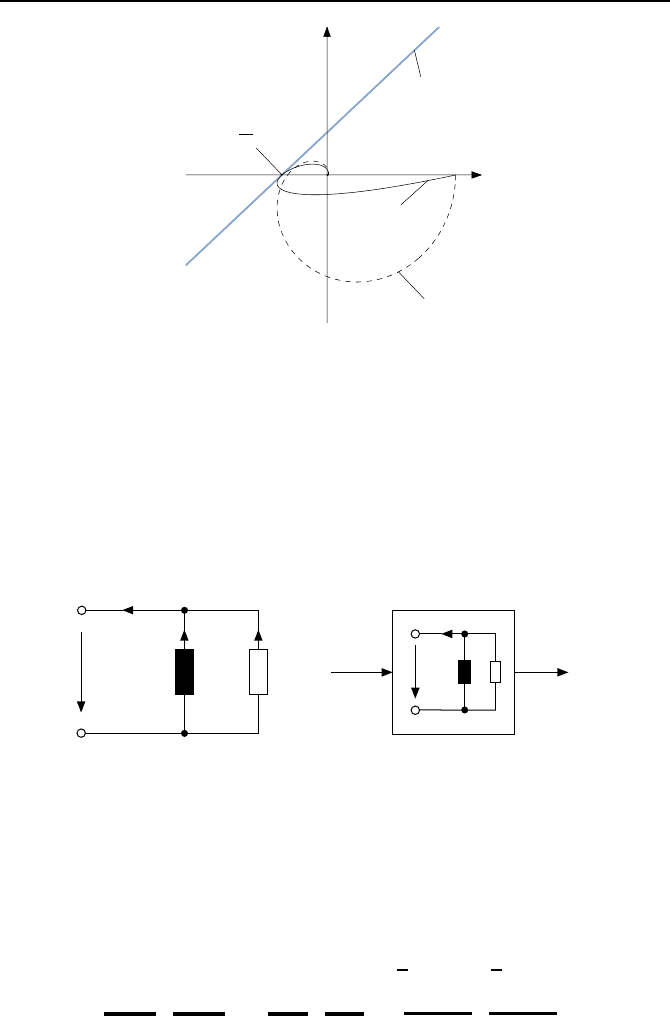
Achse, so ist der Regelkreis absolut stabil. Bild 2.44 illustriert den Zusam-

menhang. Auch hier legt man die Gerade tangential an die Zypkin-Ortskurve,

so dass sich der gr

oßtm

ogliche Stabilit

atssektor ergibt.

2.3. Hyperstabilit

at 81

kritische

Zypkin-

Gerade

Zypkin-

Ortskurve

G(e

jωT

)

G(jω)

Bild 2.44: Anwendung des allgemeinen Zypkin-Kriteriums.

2.3 Hyperstabilit

2.3.1 Der Begriﬀ der Hyperstabilit

Der Begriﬀ Hyperstabilit

at wurde 1963 von V. M. Popov [153, 154] eingef

uhrt.

Um einen Zugang zu diesem Stabilit

atsbegriﬀ zu ﬁnden, wird zuerst das ein-

fache lineare System mit Widerstand R und Spule L in Bild 2.45 betrachtet.

(a)

uy= i

(b)

Bild 2.45: RL-Schaltung: (a) Schaltplan, (b) Blockschaltbild mit Eingangsgr

oße u

und Ausgangsgr

oße y = i.

Die Energiebilanz dieses Systems hat die Form

−



u(τ)i(τ) dτ



 

zugef

uhrte

Energie



(τ) dτ



 

verbrauchte

Energie

(t) −

(0)



 

gespeicherte

Energie

Aus obiger Gleichung ergibt sich die Absch

atzung

82 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

−



u(τ) · i(τ) dτ ≥



(t) − i

(0)



ur die zugef

uhrte Energie. Hierbei ist anzumerken, dass die zugef

uhrte Ener-

gie positiv ist, wenn Energie vom System aufgenommen wird. Ist sie negativ,

so gibt das System Energie ab.

Da die in der Spule gespeicherte Energie endlich ist, kann man sicher f

alle t ≥ 0auchdieAbsch

atzung

−



u(τ) · i(τ) dτ ≥

L(i

(t) − i

(0)) ≥−ε

(2.7)

treﬀen. Diese Absch

atzung bedeutet, dass die dem System zugef

uhrte Energie

beliebig (positiv) groß werden kann. Eben gr

oßer als −ε

. Ist die zugef

uhrte

Energie negativ, d. h., entnimmt man dem System gespeicherte Energie, so ist

die Energieentnahme auf einen Wert gr

oßer −ε

beschr

ankt. Denn sonst h

atte

man ein Perpetuum mobile erster Art. Betrachtet man nun u als Eingangs-

oße und y = i als Ausgangsgr

oße, dann erh

alt man als Energieabsch

atzung

aus Gl. (2.7)



u(τ) · y(τ) dτ ≤ ε

ur alle t ≥ 0. (2.8)

Es ist nun sicher sinnvoll, die Energieabsch

atzung (2.8) auf beliebige li-

neare Systeme

˙x = Ax + Bu,

y = Cx + Du

zu erweitern. Man benutzt sie also als Forderung an die Ein- und Ausgangs-

oßen linearer MIMO-Systeme. Sie ist dann nur noch im

ubertragenen Sinn

eine Energieabsch

atzung.

Die Eingangs- und die zugeh

origen Ausgangsgr

oßenvektoren sollen in der

verallgemeinerten Form der Absch

atzung



(τ) · y(τ ) dτ ≤ ε

ur alle t ≥ 0 (2.9)

gen

ugen. Ersichtlich muss

dim y =dimu

gelten, da sonst in Gl. (2.9) das Skalarprodukt nicht gebildet werden kann.

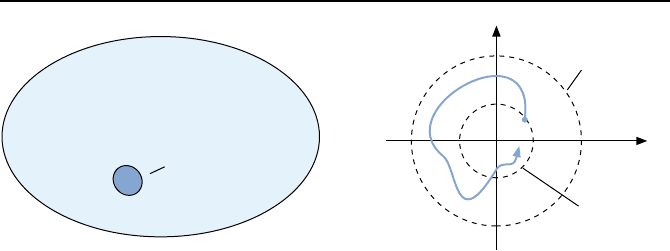
Die Ungleichung (2.9) deﬁniert eine Menge von Funktionen u(t), die f

ur obiges

System als Eingangsfunktionen zugelassen werden. Bild 2.46 illustriert dies.

2.3. Hyperstabilit

at 83

Menge aller

Funktionen u(t)

Menge aller

Funktionen,

die Gl. (2.9)

erf

ullen

Bild 2.46: Die Menge aller zugelassenen

Funktionen u(t).

x(t)

Radius

+ ε

|x(0)|

Radius |x(0)|

Bild 2.47: Stabilit

atsanforderung an hy-

perstabile Systeme.

Interessant sind nun Systeme, die f

ur alle diejenigen Eingangsfunktionen

u(t) stabil sind, welche die Integralungleichung (2.9) erf

ullen. Stabil heißt hier,

dass der Zustandsvektor x(t)f

ur jede zul

assige Funktion u(t) bei beliebigem

Anfangsvektor x(0) gem

aß

|x(t)|≤ε

+ ε

|x(0)|,ε

> 0,ε

> 0,

beschr

ankt bleibt. Die beiden beliebigen positiven Konstanten ε

und ε

legen

den Radius des Gebietes fest, in dem x(t)f

ur alle t ≥ 0 verbleibt. Bild 2.47

illustriert die Situation. Systeme dieser Art nennt man hyperstabil.Zusam-

mengefasst lautet die Deﬁnition der Hyperstabilit

at f

ur zeitinvariante lineare

Systeme:

Deﬁnition 9 (Hyperstabilit

at). Gegeben sei das steuerbare und beobacht-

bare zeitinvariante System

˙x = Ax + Bu,

y = Cx + Du

mit dim u =dimy. Wenn dann f

ur alle Eingangsfunktionen u(t) und die

resultierenden Ausgangsfunktionen y(t), welche die Ungleichung



(τ) · y(τ ) dτ ≤ ε

ur alle t ≥ 0

erf

ullen, und f

ur alle Anfangsvektoren x(0) ∈ IR

die Absch

atzung

|x(t)|≤ε

+ ε

|x(0)| f

ur alle t ≥ 0

gilt, dann heißt das System hyperstabil. Dabei sind ε

und ε

positive Kon-

stanten.