J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

1.1. Systembeschreibung und Systemverhalten 3

kann Gl. (1.1) auch als Vektordiﬀerenzialgleichung

˙x = f(x, u)=

⎡

⎢

⎣

h(x

,...,x

,...,u

)

⎤

⎥

⎦

dargestellt werden.

Systeme mit nur einer Eingangsgr

oße u und einer Ausgangsgr

oße y be-

zeichnet man als Eingr

oßensysteme oder SISO-Systeme (engl. single-input,

single-output). Systeme mit mehreren Eingangsgr

oßen und Ausgangsgr

oßen

werden als Mehrgr

oßensysteme oder MIMO-Systeme (engl. multiple-input,

multiple-output) bezeichnet.

In der Regelungstechnik sind vor allem drei Typen nichtlinearer Regelungs-

systeme von Bedeutung. Die erste Klasse bilden lineare Regler f

ur nichtlineare

Regelstrecken, wie sie Bild 1.2 zeigt. Sie fallen oft in die Kategorie linearer Reg-

lerentwurfsmethoden, denn in diesem Fall ist die Regelstrecke linearisierbar

und das linearisierte Modell hinreichend genau. Dann kann die lineare Sys-

temtheorie zum Einsatz kommen. Wir bezeichnen dabei die F

uhrungsgr

oße

mit w und die Regelabweichung mit e. Im MIMO-Fall verwenden wir fett

gedruckte Buchstaben w und e.

linearer

Regler

nichtlineare

Regelstrecke

Bild 1.2: Nichtlineare Regelstrecke mit linearem Regler.

Die zweite Klasse stellen nichtlineare Regler f

ur lineare Regelstrecken dar,

wie sie Bild 1.3 zeigt. Oft werden einfache nichtlineare Regler aus technischen

unden oder der Kosten wegen f

ur lineare Regelstrecken eingesetzt. Ein weit-

verbreitetes Beispiel ist etwa die Temperaturregelung in B

ugeleisen mit einem

lineare

Regelstrecke

nichtlinearer

Regler

Bild 1.3: Lineare Regelstrecke mit nichtlinearem Regler.

4 Kapitel 1. Grundlagen nichtlinearer Systeme

nichtlineare

Regelstrecke

nichtlinearer

Regler

Bild 1.4: Nichtlineare Regelstrecke mit nichtlinearem Regler.

Bimetall. Das Bimetall hat die Charakteristik eines Schalters mit Hysterese,

d. h., es ist ein nichtlineares System. Nichtlineare Regler komplizierter Bauart

werden ebenfalls f

ur lineare Regelstrecken eingesetzt, um bessere Regelergeb-

nisse zu erzielen, als es mit linearen Reglern m

oglich w

are.

Die dritte Klasse bilden nichtlineare Regler f

ur nichtlineare Regelstrecken,

wie in Bild 1.4 dargestellt. Nichtlineare Regelstrecken sind oft sehr komplex in

ihrem Verhalten. Eine lineare Regelung kann dann vielfach die gew

unschte Re-

gelqualit

at nicht erzeugen. In diesem Fall muss eine geeignete nichtlineare Re-

gelung entworfen werden. Beispielsweise ist es in bestimmten F

allen m

oglich,

eine nichtlineare Regelstrecke mit einem nichtlinearen Regler so zu kombinie-

ren, dass ein linearer Regelkreis entsteht. Sein Verhalten ist dann aufgrund

der Linearit

at einfach zu durchschauen.

1.1.3 Ruhelagen nichtlinearer Systeme

Eines der zentralen Ziele der Regelungstechnik ist es, den Zustand einer Re-

gelstrecke in eine Ruhelage zu bringen und ihn dort zu halten. Beispielsweise

will man ein Flugzeug mittels eines Autopiloten auf eine bestimmte H

ohe,

das Wasser eines Boilers auf eine bestimmte Temperatur oder ein gewalztes

Blech auf eine vorgegebene Dicke bringen und dort halten. F

ur den Entwurf

eines geeigneten Reglers muss man also zuerst eine Ruhelage ausﬁndig ma-

chen. Dabei stellt sich die Frage, wie man eine Ruhelage eines nichtlinearen

Systems ermittelt. Bevor diese Frage n

aher untersucht wird, soll der Begriﬀ

der Ruhelage genauer deﬁniert werden.

Deﬁnition 1 (Ruhelage). Gegeben sei das System

˙x = f (x, u).

Dann heißt ein Punkt x

des Zustandsraumes Ruhelage, wenn

˙x = f(x

, 0)=0

gilt.

In dieser Deﬁnition wurde

u = 0

1.1. Systembeschreibung und Systemverhalten 5

vorausgesetzt. Selbstverst

andlichkannesauchF

alle geben, in denen

u = c = 0

ist, wobei c ∈ IR

ein konstanter Vektor ist und

˙x = f(x, u = c)=0

gilt. Dieser Fall ist durch obige Deﬁnition abgedeckt, wenn man die Transfor-

mation

u = ˜u + c

durchf

uhrt. Dann hat man das System

˙x =

f(x, ˜u)

zu untersuchen, und dieses hat f

ur ˜u = 0 eine Ruhelage in x

. D. h., es gilt

˙x =

f(x

, 0)=0.

Das Auﬃnden einer Ruhelage eines nichtlinearen Systems ist oftmals nicht

einfach. Man hat n

amlich die implizite Gleichung

˙x = f(x

, 0)=0

nach x

aufzul

osen. Es kann eine, keine oder mehrere L

osungen geben. Auch

ein L

osungskontinuum ist m

oglich. Dies ist in Bild 1.5 f

ur eine eindimensionale

Funktion f illustriert.

Bei der konkreten Berechnung von Ruhelagen x

onnen dann die folgen-

den drei F

alle auftreten. Im ersten Fall ist die implizite Gleichung

Kontinuum von L

osungen

eine L

osung mehrere L

osungen

keine L

osung

Bild 1.5: M

ogliche L

osungsmengen der Ruhelagengleichung f(x

, 0) = 0.

6 Kapitel 1. Grundlagen nichtlinearer Systeme

f(x

, 0)=0

explizit nach x

auﬂ

osbar, d. h., es gilt

= f

−1

(0).

Im zweiten Fall ist die implizite Gleichung transzendent. Dann muss

man auf numerische Verfahren, wie das mehrdimensionale Newton-Verfahren,

zur

uckgreifen. Insbesondere steht man oft vor dem Problem, dass man nicht

weiß, wieviele Ruhelagen existieren oder ob es

uberhaupt welche gibt.

Der dritte Fall betriﬀt viele technische Systeme. Bei ihnen k

onnen wir

oft aus der Anschauung oder der Systemkenntnis heraus eine Ruhelage x

erahnen. Durch Einsetzen in die Systemgleichung l

asst sich die Annahme

uberpr

ufen.

1.1.4 Beispiel Satellit

Wir betrachten die Rotation eines Satelliten bzw. einer Weltraumsonde. Die-

sen k

onnen wir

uber Steuerd

usen um seine Achsen drehen. Bild 1.6 zeigt

einen entsprechenden Satelliten mit seinem k

orperfesten Koordinatensystem

(x, y, z) und einem raumfesten Koordinatensystem (˜x, ˜y, ˜z).

ur den Drehimpulsvektor L des Satelliten, der sich mit seinem k

orperfes-

ten Koordinatensystem und dem Winkelgeschwindigkeitsvektor ω gegen

uber

dem raumfesten Koordinatensystem dreht, gilt mit dem Tr

agheitstensor J die

Beziehung

L = Jω.

Die Bewegungsgleichung leitet sich aus

= M (1.2)

ab, wobei der Drehmomentvektor M die durch die Steuerd

usen verursachten

Drehmomente enth

alt. F

ur die Ableitung des Drehimpulses L nach der Zeit

gilt

= J ˙ω + ω × (Jω), (1.3)

wobei der Term ω×(Jω) aus der mit ω erfolgenden Drehung des k

orperfesten

gegen

uber dem raumfesten Koordinatensystem resultiert. Aus Gl. (1.2) und

Gl. (1.3) folgt

J ˙ω = −ω × (Jω)+M . (1.4)

Sind die Achsen des k

orperfesten Koordinatensystems des Satelliten mit

seinen Haupttr

agheitsachsen identisch, so gilt

J =

⎡

⎣

0 J

00J

⎤

⎦

1.1. Systembeschreibung und Systemverhalten 7

˜z

˜x

˜y

Bild 1.6: Satellit mit k

orperfestem Koordinatensystem (x, y, z) und raumfestem Ko-

ordinatensystem (˜x, ˜y, ˜z). Mittels der Euler-Winkel α, β, γ kann die Orientierung

des Satelliten bez

uglich des raumfesten Koordinatensystems angegeben werden.

In diesem Fall ergeben sich aus Gl. (1.4) die Euler’schen Kreiselgleichungen

˙ω

= −(J

− J

)ω

+ M

˙ω

= −(J

− J

)ω

+ M

˙ω

= −(J

− J

)ω

+ M

als Bewegungsgleichungen des Systems.

Oﬀensichtlich hat der Satellit nur dann eine Ruhelage, d. h., es gilt nur

dann

ω = 0, wenn mindestens zwei der Winkelgeschwindigkeiten ω

, ω

und

gleich null sind. Dabei setzen wir voraus, dass die Stellgr

oßen M

, M

und

ebenfalls gleich null sind. Insgesamt ergeben sich so die drei Ruhelagen-

bereiche

⎡

⎣

⎤

⎦

, ω

⎡

⎣

⎤

⎦

, ω

⎡

⎣

⎤

⎦

8 Kapitel 1. Grundlagen nichtlinearer Systeme

Dabei k

onnen die Winkelgeschwindigkeiten ω

, ω

∈ IR beliebige Werte

annehmen. Insgesamt existieren also unendlich viele Ruhelagen. Man beachte,

dass auch der Fall ω

= ω

=0m

oglich ist, d. h., auch ω = 0 ist eine

Ruhelage.

Das Beispiel illustriert auch, dass der Begriﬀ Ruhelage nicht zwingend die

Abwesenheit von Bewegung, hier bei einem starren K

orper, impliziert. Viel-

mehr bedeutet der Begriﬀ Ruhelage, dass sich die Zust

ande des betrachteten

Systems nicht mit der Zeit

andern.

Wir wollen nun noch die Orientierung des Satelliten im raumfesten Koor-

dinatensystem beschreiben. Dies geschieht mittels der Euler-Winkel α, β und

γ [79, 88], die im Bild 1.6 dargestellt sind und die wir im Vektor ϕ =[αβγ]

zusammenfassen. Die Bewegungsgleichungen des Satelliten lauten dann



˙ϕ

˙ω





Λ(ϕ)ω

−J

−1

[ω × (Jω)]





−1



M, (1.5)

wobei die Matrix

Λ(ϕ)=

⎡

⎣

1sin(α)tan(β)cos(α)tan(β)

0cos(α) −sin(α)

0sin(α)/ cos(β)cos(α)/ cos(β)

⎤

⎦

den Winkelgeschwindigkeitsvektor ω in den Winkelgeschwindigkeitsvektor ˙ϕ

des raumfesten Koordinatensystems transformiert. Die Transformation ˙ϕ =

Λ(ϕ)ω ist dabei abh

angig von den Euler-Winkeln, d. h. von ϕ.DasSystem

(1.5) besitzt oﬀensichtlich wieder, wenn f

ur den Stellgr

oßenvektor M = 0 gilt,

unendlich viele Ruhelagen



= 0



mit ϕ

∈ IR

In diesem Fall f

uhrt der Satellit allerdings keine Bewegung um eine seiner

Achsen aus.

1.1.5 Ruhelagen linearer Systeme

Lineare Systeme

˙x = Ax + Bu,

y = Cx + Du

bilden einen Sonderfall der allgemeinen Systembeschreibung

˙x = f (x, u),

y = g(x, u)

und sollen im Folgenden kurz betrachtet werden, um die Unterschiede zu

nichtlinearen Systemen aufzuzeigen.

1.1. Systembeschreibung und Systemverhalten 9

u =0

Kontinuum

von Ruhelagen

Bild 1.7: Das System 1/s

und seine Ruhelagen x

=[a 0]

mit a ∈ IR.

Die Ruhelagen linearer Systeme sind einfach aus der Gleichung

˙x = Ax

= 0

zu ermitteln, wenn u = 0 gilt. Folgende F

alle k

onnen auftreten: Gilt det(A) =

0, dann gibt es nur die Ruhelage

= 0.

Gilt det(A) = 0, dann besitzt A Eigenwerte mit dem Wert null, und es gibt

einen linearen Unterraum von Vektoren x

ur die

= 0

gilt. Es gibt also ein Kontinuum von Ruhelagen. Ein einfaches Beispiel ist das

System

˙x =





x +





das aus zwei Integratoren besteht, also die

Ubertragungsfunktion 1/s

besitzt.

Oﬀensichtlich bilden alle Zust

ande





,a∈ IR,

Ruhelagen. D. h., die x

-Achse bildet ein Kontinuum von Ruhelagen, wie es

Bild 1.7 illustriert.

Angemerkt sei, dass f

ur u = c und det(A) = 0 der Fall auftreten kann, dass

keine Ruhelage existiert. N

amlich dann, wenn Ax = −Bc ein

uberbestimmtes

Gleichungssystem ist. Ein lineares System hat also entweder eine, keine oder

ein Kontinuum von Ruhelagen. Der Fall mehrerer isolierter Ruhelagen, wie er

bei nichtlinearen Systemen m

oglich ist, kommt nicht vor.

1.1.6 Stabilit

at von Ruhelagen

Als stabil bezeichnet man eine Ruhelage, wenn alle Trajektorien x(t), die

in einer Umgebung der Ruhelage beginnen, mit zunehmender Zeit in diese

10 Kapitel 1. Grundlagen nichtlinearer Systeme

Ruhelage hineinlaufen. In einer abgeschw

achten Version benutzt man den Be-

griﬀ stabil auch dann noch, wenn die Trajektorien zwar nicht in die Ruhelage

laufen, aber in einer n

aheren Umgebung der Ruhelage verbleiben.

Wir betrachten im Weiteren zuerst einige Beispiele stabiler und instabiler

Ruhelagen, um einen Eindruck zu bekommen und ein erstes Verst

andnis zu

entwickeln. Am einfachsten gelingt dies anhand linearer Systeme ˙x = Ax mit

der Ruhelage x

= 0.DaindenL

osungen x(t) linearer Diﬀerenzialgleichun-

gen ˙x = Ax nur Terme

und t

mit k ∈{1, 2, 3,...}

enthalten sind, laufen alle Trajektorien x(t) des Systems f

ur t →∞oﬀen-

sichtlich in die Ruhelage x

= 0,wennf

ur jeden Eigenwert λ

des Systems

Re {λ

} < 0

gilt. Man bezeichnet dann nicht nur die Ruhelage, sondern auch das System

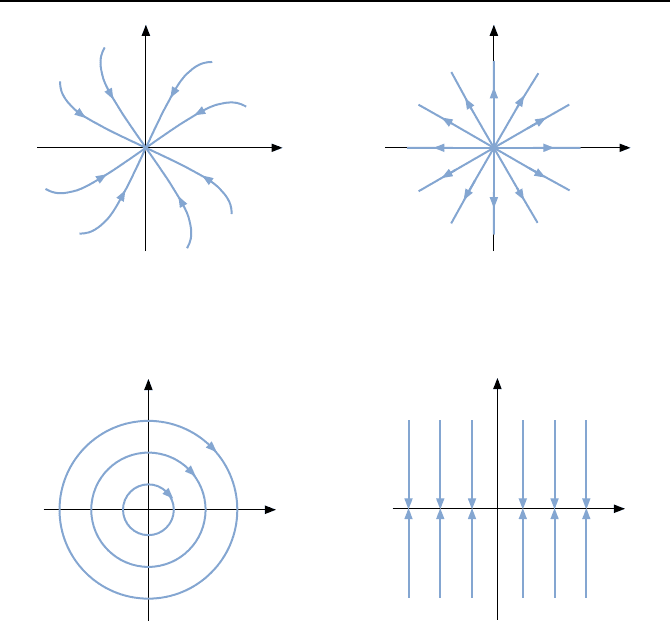
als stabil. Bild 1.8 zeigt die Trajektorien eines solchen linearen Systems.

Gilt dagegen f

ur mindestens einen Eigenwert

Re {λ

} > 0,

so ist die Ruhelage instabil, denn dann streben Trajektorien von ihr weg.

Daher wird ein solches lineares System auch als instabil bezeichnet. Bild 1.9

zeigt ein Beispiel.

ur den Fall eines Systems mit einem Paar konjugiert komplexer Eigen-

werte λ

1/2

= ±j liegt ein harmonischer Oszillator vor, dessen Trajektorien

Bild 1.10 zeigt. Oﬀensichtlich laufen die Trajektorien weder in die Ruhelage

= 0 noch ins Unendliche. Auch hier besitzt die Ruhelage x

= 0 also

noch eine gewisse Stabilit

at.

Ahnlich gelagert ist der Fall eines Systems zwei-

ter Ordnung mit einem Eigenwert λ

= 0 und einem Eigenwert λ

< 0, wie

ihn Bild 1.11 veranschaulicht. Zwar laufen alle Trajektorien in eine Ruhelage

auf der x

-Achse, aber keine Ruhelage zieht alle Trajektorien an. Es laufen al-

lerdings auch keine Trajektorien ins Unendliche, weshalb man solche Systeme

oft auch noch als stabil bezeichnet.

Um einen ersten Eindruck der Stabilit

atsverh

altnisse bei nichtlinearen Sys-

temen zu bekommen, wird das System

˙x

= x

− 1),

˙x

= x

− 1)

(1.6)

als Beispiel betrachtet. Es besitzt zwei Ruhelagen bei





und x





Hier zeigt sich der schon erw

ahnte Unterschied zu linearen Systemen. Es gibt

zwei isolierte Ruhelagen. Das ist bei linearen Systemen nicht m

oglich. Sie be-

sitzen entweder eine Ruhelage in x

= 0 oder ein Kontinuum von Ruhelagen.

1.1. Systembeschreibung und Systemverhalten 11

Bild 1.8: Trajektorien eines stabilen li-

nearen Systems, d. h. mit Re {λ

} < 0,

Re {λ

} < 0.

Bild 1.9: Trajektorien eines instabilen li-

nearen Systems mit Eigenwerten λ

, λ

wobei Re {λ

} > 0, Re {λ

} > 0.

Bild 1.10: Trajektorien eines harmoni-

schen Oszillators, d. h. mit λ

1/2

= ±j.

Bild 1.11: Trajektorien eines Systems

mit λ

= 0 und λ

< 0.

Bild 1.12 gibt den Verlauf der Trajektorien des Systems (1.6) im Umfeld

der Ruhelagen wieder. Die Trajektorien streben in die Ruhelage x

= 0

hinein. Man kann diese Ruhelage als stabil bezeichnen. Von der Ruhelage

=[11]

streben Trajektorien weg ins Unendliche, d. h., die Ruhelage

muss als instabil angesehen werden.

Das Beispiel zeigt, dass man nichtlineare Systeme im allgemeinen Fall nicht

als stabil oder instabil bezeichnen kann, wie es bei linearen Systemen m

oglich

ist. Man muss vielmehr das Stabilit

atsverhalten des Systems in der Umge-

bung einer Ruhelage betrachten, d. h. das Stabilit

atsverhalten der Ruhelage.

In diesem Zusammenhang besteht Kl

arungsbedarf zu

(1) dem Verhalten der Trajektorien in der Umgebung einer Ruhelage,

(2) der Gr

oße des Gebiets um eine Ruhelage herum, in dem alle in diesem

Gebiet startenden Trajektorien in die Ruhelage streben, und

(3) der mathematischen Deﬁnition der Stabilit

at einer Ruhelage.

12 Kapitel 1. Grundlagen nichtlinearer Systeme

-2

-1

-2 - 1

Zustand x

Bild 1.12: Verlauf der Trajektorien des

Systems (1.6).

˜x

Bild 1.13: Transformation einer Ruhe-

lage x

in den Ursprung.

Bevor die obigen drei Probleme gekl

art werden, soll noch eine Vereinfa-

chung der Betrachtungen durchgef

uhrt werden. Hat man eine Ruhelage x

ur ein System ermittelt, so kann man sie durch die Transformation

x = x

+ ˜x

in den Ursprung, also nach ˜x = 0, verschieben. Die Systemgleichungen sind

dann durch

˜x = f (x

+ ˜x, u)=

f(˜x, u),

y = g(x

+ ˜x, u)=˜g(˜x, u)

gegeben. Da diese Transformation immer m

oglich ist, wird im Weiteren ange-

nommen, dass die interessierende Ruhelage nach null verschoben wurde. Das

Bild 1.13 illustriert die Transformation.

Um das Verhalten der Trajektorien eines Systems in der N

ahe der Ruhelage

= 0 zu kennzeichnen, wird zuerst einmal der Begriﬀ der Attraktivit

eingef

uhrt.

Deﬁnition 2 (Attraktivit

at). Ein System

˙x = f(x, u)

besitze die Ruhelage x

= 0. Dann heißt die Ruhelage x

= 0 lokal attraktiv,

wenn es eine Umgebung U (0) der Ruhelage gibt, so dass jeder Anfangswert

∈ U(0)

zu einer Trajektorie x(t) des freien Systems, d. h. u = 0,f

uhrt, die mit t→∞

in die Ruhelage x

= 0 strebt.