J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.


1.1. Systembeschreibung und Systemverhalten 23
rechte Seite der Differenzialgleichung (1.13) bzw. (1.14) aufgrund der Trans-
formation unstetig ist. Die L
¨
osung der Differenzialgleichung w
¨
are dann in den
Unstetigkeitsstellen nicht definiert.
Die Bestimmung einer Transformation z = q(x)bzw.x = q
−1
(z), die
einen Koordinatenwechsel so vornimmt, dass sich eine gew
¨
unschte System-
darstellung ergibt, ist in der Regel mit Aufwand verbunden. Dies ist schon
im linearen Fall so, wenn man z. B. ein System diagonalisieren m
¨
ochte. Denn
hierzu muss man seine Eigenvektoren bestimmen, aus denen die Transforma-
tionsmatrix T spaltenweise besteht. Im nichtlinearen Fall ist der Aufwand zur
Bestimmung der Transformationsvorschrift oft noch viel gr
¨
oßer.
F
¨
ur ein lineares System (1.8) und eine lineare Transformation (1.9) l
¨
asst
sich leicht zeigen, dass aus Gleichung (1.13) die transformierte Systemdarstel-
lung (1.10) folgt. Denn es gilt
x = q
−1
(z)=Tz und
∂q
−1
(z)
∂z
= T .
Wir wollen nun noch ein nichtlineares Beispiel zur Illustration betrachten.
Gegeben sei das System
˙x =
1
x
. (1.15)
Diese Differenzialgleichung ist in x = 0 nicht definiert. Wir werden daher
im Weiteren den Punkt x = 0 aus unseren Betrachtungen ausschließen. Als
Transformation verwenden wir
z = q(x)=e
sgn(x)x
2
/2
(1.16)
bzw.
x = q
−1
(z)=sgn
ln
z
2
ln
z
2
1/2
. (1.17)
Die Transformationsvorschriften (1.16) und (1.17) sind eineindeutig, stetig
differenzierbar und q bildet den reellen Zahlenraum IR in das Intervall (0, ∞)
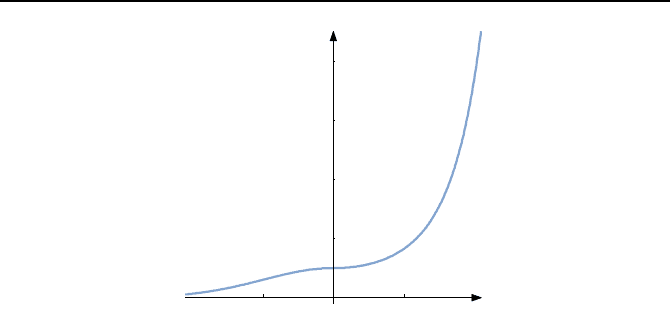
ab. Bild 1.25 zeigt den Verlauf von q(x). Wir bilden nun die Ableitung
∂q
−1
(z)
∂z
=
ln
z
2
−1/2
z
und erhalten gem
¨
aß Gl. (1.13) f
¨
ur das transformierte System
˙z =
ln
z
2
−1/2
z
−1
·
1
sgn (ln (z
2
)) |ln (z
2
)|
1/2
,
d. h.
˙z = z sgn
ln
z
2
=
z, z > 1,
−z, 0 <z<1.
(1.18)
24 Kapitel 1. Grundlagen nichtlinearer Systeme
8
6
4
2
e
sgn(x)x
2
/2
-1
0
1
x
q(x)
Bild 1.25: Verlauf der Funktion z = q(x).
Es ist uns also mittels der Transformation (1.16) gelungen, die nichtlineare
Systemdarstellung (1.15) in eine – genauer gesagt zwei – lineare umzuwandeln.
Man beachte, dass beide Darstellungen
¨
aquivalent zueinander sind, da die
Transformation eineindeutig ist.
Abschließend bestimmen wir noch die L
¨
osung der Differenzialgleichung
(1.15), indem wir zuerst Gl. (1.18) l
¨
osen. Deren L
¨
osung ist
z(t)=
z
0
e
t
,z>1,
z
0
e
−t
, 0 <z<1,
mit dem Anfangswert z
0
= z(0). Durch Transformation mittels Gl. (1.16)
erhalten wir die L
¨
osung des nichtlinearen Systems (1.15) zu
x(t)=q
−1
(z(t)) =
sgn
ln
z
2
0
e
2t
·
ln
z
2
0
e
2t
1/2
,z>1,
sgn
ln
z
2
0
e
−2t
·
ln
z
2
0
e
−2t
1/2
, 0 <z<1.
(1.19)
Wir ersetzen noch den Anfangswert z
0
durch den Anfangswert x(0) = x
0
.
Dazu bilden wir
x(0) = sgn
ln
z
2
0
·
ln
z
2
0
1/2
,
woraus
sgn(x
0
)=sgn
ln
z
2
0
und mit Gl. (1.16)
x
2
0
=ln
z
2
0
,z
0
> 1,
−x
2
0
=ln
z
2
0
, 0 <z
0
< 1,
folgt. Setzt man diese Ergebnisse in Gl. (1.19) ein, so erh
¨
alt man schließlich

1.1. Systembeschreibung und Systemverhalten 25
x(t)=
sgn (x
0
) ·
x
2
0
+2t
1/2
,x
0
> 0,
sgn (x
0
) ·
−x
2
0
− 2t
1/2
,x
0
< 0,
=sgn(x
0
) ·
x
2
0
+2t
1/2
,x=0,
als L
¨
osung von ˙x =1/x.
Im Allgemeinen ist es m
¨
oglich, dass die Transformationsgleichung auch
eine Abh
¨
angigkeit vom Eingangsvektor u und eventuell seinen zeitlichen Ab-
leitungen u
(j)
, j =1,...,i, aufweist. D. h., sie hat die Form
z = q(x, u, ˙u,...,u
(i)
)
bzw.
x = q
−1
(z, u, ˙u,...,u
(i)
). (1.20)
Transformieren wir nun das System ˙x = f (x, u)inz-Koordinaten, so gilt
nach Einsetzen von Gl. (1.20) in die Systemgleichung
dq
−1
(z,u,...,u
(i)
)
dt
=
∂q
−1
(z,u,...,u
(i)
)
∂z
· ˙z+
i
j=0
∂q
−1
(z,u,...,u
(i)
)
∂u
(j)
· u
(j+1)
= f(q
−1
(z,u,...,u
(i)
), u).
Hieraus ergibt sich die transformierte Systembeschreibung
˙z =
∂q
−1
(z,u,...,u
(i)
)
∂z
−1
·
⎛
⎝
f(q
−1
(z,u,...,u
(i)
),u)−
i
j=0
∂q
−1
(z,u,...,u
(i)
)
∂u
(j)
u
(j+1)
⎞
⎠
.
Auf
¨
ahnliche Weise l
¨
asst sich die Gleichung der R
¨
ucktransformation herleiten.
1.1.11 Zeitdiskrete Systeme
Neben zeitkontinuierlichen Systemen begegnen uns in der Regelungstechnik
auch Systeme, bei denen die Eingangs-, Ausgangs- und Zustandsgr
¨
oßen nicht
kontinuierlich
¨
uber die Zeit betrachtet werden, sondern nur zu bestimmten,
d. h. diskreten Zeitpunkten k [49, 57, 81, 82, 104]. Beschrieben werden diese
zeitdiskreten Systeme durch Iterations- bzw. Differenzengleichungen
x(k +1)=f (x(k), u(k)),
y(k)=g(x(k), u(k))
(1.21)
mit k =0, 1, 2,... Analog zu den kontinuierlichen Systemen ist x der n -
dimensionale Zustandsvektor, u der m - dimensionale Eingangsvektor und y
der r - dimensionale Ausgangsvektor.
Die Ruhelagen x
R
eines zeitdiskreten Systems sind durch das Gleichungs-
system

26 Kapitel 1. Grundlagen nichtlinearer Systeme
x
R
= f(x
R
, 0)
definiert. Dabei ist, wie im zeitkontinuierlichen Fall, ohne Einschr
¨
ankung der
Allgemeinheit u = 0 vorausgesetzt. Auch im vorliegenden Fall ist das Glei-
chungssystem wieder nichtlinear.
Die Stabilit
¨
at einer Ruhelage l
¨
asst sich
¨
ahnlich wie im zeitkontinuierlichen
Fall definieren. Es sei wieder vorausgesetzt, dass die Ruhelage in x = 0 liegt.
Definition 6 (Stabilit
¨
at von Ruhelagen zeitdiskreter Systeme). Ein
System
x(k +1)=f (x(k), u(k))
besitze die Ruhelage x
R
= 0. Dann heißt die Ruhelage stabil im Sinne von
Ljapunov, wenn es zu jeder ε-Umgebung
U
ε
(0)={x ∈ IR
n
||x| <ε}
eine δ-Umgebung
U
δ
(0)={x ∈ IR
n
||x| <δ}
gibt, so dass alle Zustandsfolgen x(k), die in der δ-Umgebung beginnen, d. h.
x(0) ∈ U
δ
(0),
in ihrem weiteren Verlauf in der ε-Umgebung bleiben, d. h.
x(k) ∈ U
ε
(0) f
¨
ur k>0.
Gilt f
¨
ur alle x(0) ∈ U
δ
(0) des Weiteren
lim
k→∞
x(k)=0,
so heißt die Ruhelage asymptotisch stabil.
Bei zeitdiskreten Systemen k
¨
onnen, wie bei zeitkontinuierlichen, auch
Grenzzyklen auftreten. Dies ist der Fall, wenn f
¨
ur eine Folge von Zustands-
vektoren x(0), x(1),..., x(l) die Beziehung
x(0) = x(l)
bei konstantem Eingangsvektor u(k)erf
¨
ullt ist. Da der Grenzzyklus x(0), x(1),
..., x(l)insgesamtl+1 Zust
¨
ande umfasst, spricht man von einem Zyklus der
L
¨
ange l +1.
Chaotisches Verhalten ist ebenfalls m
¨
oglich. Beispielsweise tritt Chaos in
einem zeitdiskreten System erster Ordnung auf, wenn ein Zyklus
x(0),x(1),x(2) = x(0),
d. h. ein Zyklus der L
¨
ange drei, existiert [115]. Erw
¨
ahnenswert ist, dass Chaos
bei zeitdiskreten Systemen ab der Systemordnung n = 1 auftreten kann. Bei

1.2. L
¨
osung nichtlinearer Differenzialgleichungen 27
zeitkontinuierlichen Systemen dagegen kann Chaos erst ab der Systemordnung
n = 3 entstehen.
Die exakte Modellierung eines abgetasteten nichtlinearen zeitkontinuierli-
chen Systems durch eine Differenzengleichung (1.21) ist in den meisten F
¨
allen
unm
¨
oglich. Diese Situation ist g
¨
anzlich anders als bei linearen Systemen, wo
man aus dem zeitkontinuierlichen Modell relativ einfach das durch Abtastung
entstehende zeitdiskrete Modell berechnen kann. Diese einfache Berechnung
resultiert aus der Kenntnis der L
¨
osung der linearen Differenzialgleichung. Im
nichtlinearen Fall verf
¨
ugt man in der Regel nicht
¨
uber die Systeml
¨
osung und
kann daher auch das zeitdiskrete Modell nicht bestimmen, zumindest nicht
exakt. N
¨
aherungsweise ist dies schon m
¨
oglich.
¨
Uber die numerische L
¨
osung
nichtlinearer Differenzialgleichungen lassen sich n
¨
amlich N
¨
aherungsmodelle
f
¨
ur abgetastete nichtlineare Systeme ermitteln. Der L
¨
osung nichtlinearer Dif-
ferenzialgleichungen widmen wir uns im n
¨
achsten Kapitel.
1.2 L
¨
osung nichtlinearer Differenzialgleichungen
1.2.1 Grundlegendes und das Verfahren von Euler-Cauchy
Die L
¨
osung nichtlinearer Differenzialgleichungen mit Anfangswerten x(t
0
) und
z. B. t
0
= 0, so genannter Anfangswertprobleme
˙x(t)=f(x(t), u(t)),
x(t
0
)=x
0
,
ist im Gegensatz zu linearen Differenzialgleichungen in den meisten F
¨
allen,
wie erw
¨
ahnt, nur numerisch m
¨
oglich. Zu diesem Zweck ist eine Reihe von
Integrationsverfahren entwickelt worden [44, 173].
Sie basieren auf dem folgenden Prinzip, das ohne Einschr
¨
ankung der All-
gemeinheit f
¨
ur den Fall nur einer Zustandsgr
¨
oße x,also
˙x(t)=f (x(t),u(t)), (1.22)
illustriert werden soll. Durch Integration von Gl. (1.22) erh
¨
alt man die L
¨
osung
der Differenzialgleichung zu
x(t)=x(t
0
)+
t
t
0
f (x(τ),u(τ )) dτ. (1.23)
Man beachte, dass diese Gleichung implizit bez
¨
uglich x(t) und daher analy-
tisch meistens nicht l
¨
osbar ist. Die Integrationsverfahren l
¨
osen das Integral
in Gl. (1.23) daher durch mehr oder weniger gute N
¨
aherungen numerisch.
Genauigkeit und Rechenaufwand h
¨
angen dabei von der Wahl des Integrati-
onsverfahrens ab.
28 Kapitel 1. Grundlagen nichtlinearer Systeme
Bei der numerischen L
¨
osung wird die Gleichung (1.23) diskretisiert, d. h.,
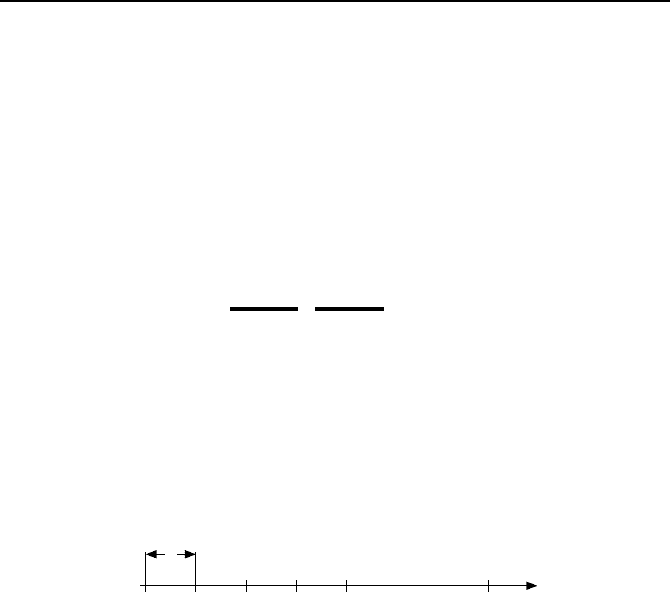
die Zeitachse wird in eine Anzahl
¨
aquidistanter St
¨
utzstellen
t
i
= t
0
+ h · i, i =0,...,n,
wie in Bild 1.26 dargestellt, eingeteilt, wobei die Intervallbreite h als Schritt-
weite bezeichnet wird. Man kann jetzt die L
¨
osung der Differenzialgleichung
(1.22) in den Zeitpunkten t
i
als Rekursionsgleichung
x(t
i+1
)=x(t
0
)+
t
i
t
0
f(x, u) dt
x(t
i
)
+
t
i
+1
t
i
f(x, u) dt,
also
x(t
i+1
)=x(t
i
)+
t
i+1
t
i
f(x, u) dt,
schreiben.
...
h
t
0
t
1
t
2
t
3
t
4
t
i
Bild 1.26: Zeitpunkte t
i
und Schrittweite h der numerischen L
¨
osung.
Ziel der Integrationsverfahren ist es, eine gute Approximation f
¨
ur das In-
tegral zu finden. Im einfachsten Fall n
¨
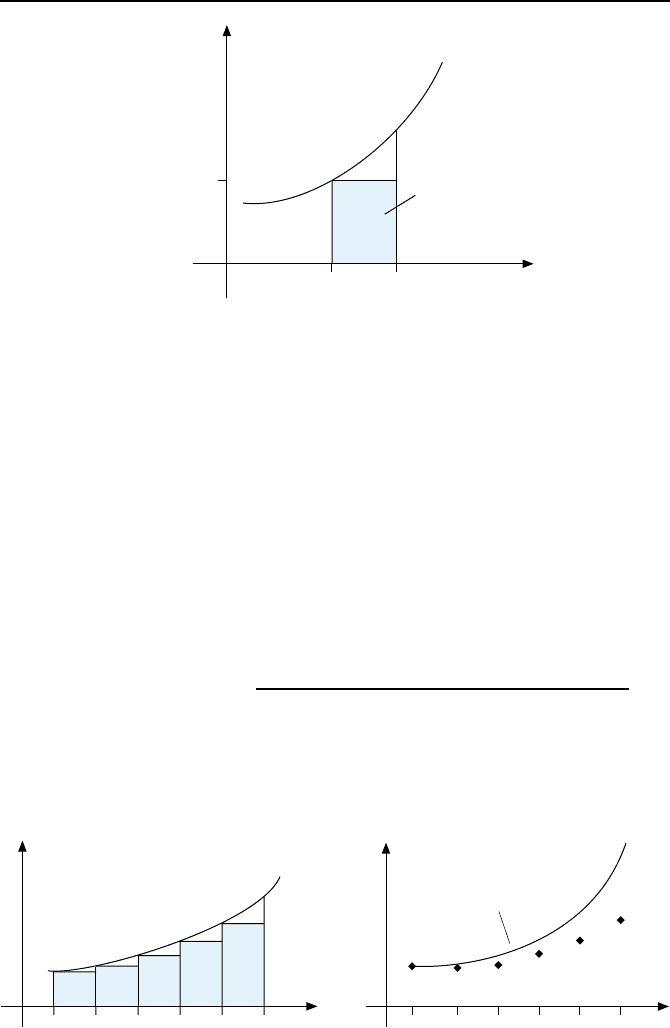
ahert man, wie in Bild 1.27 dargestellt,
die Fl
¨
ache
F =
t
i+1
t
i
f(x, u)dt
zwischen t
i
und t
i+1
durch ein Rechteck mit dem Fl
¨
acheninhalt
F
app
= h · f (x(t
i
),u(t
i
))
an und erh
¨
alt als N
¨
aherung f
¨
ur x(t
i+1
)denWert
ˆx(t
i+1
)=ˆx(t
i
)+h · f (ˆx(t
i
),u(t
i
)).
F
¨
ur den mehrdimensionalen Fall und mit den Abk
¨
urzungen ˆx(t
i
)=ˆx
i
bzw. u(t
i
)=u
i
gilt
1.2. L
¨
osung nichtlinearer Differenzialgleichungen 29
f
t
f(x(t
i
),u(t
i
))
t
i
t
i+1
h · f(x(t
i
),u(t
i
))
F
app
Bild 1.27: N
¨
aherungsl
¨
osung des Integrals.
ˆx
i+1
= ˆx
i
+ h · f (ˆx
i
, u
i
).
Als Anfangswert f
¨
ur diese Rekursionsformel dient ˆx
0
= x
0
. Obiges Verfah-
ren bezeichnet man als Polygonzugverfahren von Euler-Cauchy.Esistein-
fach, aber ungenau. Bild 1.28 illustriert die N
¨
aherung mit dem Euler-Cauchy-
Verfahren.
1.2.2 Genauigkeit der numerischen L
¨
osung
Die N
¨
aherung der Fl
¨
ache unter der Kurve durch die Rechtecke hat direkten
Einfluss auf die Genauigkeit der L
¨
osung, wie Bild 1.29 illustriert. Der Fehler
im Schritt i,
ε
i
= ||x(t
i
) − ˆx(t
i
)|| =
(x
1
(t
i
) − ˆx
1
(t
i
))
2
+ ...+(x
n
(t
i
) − ˆx
n
(t
i
))
2
,
ist offensichtlich abh
¨
angig von der Anzahl aller vorherigen Schritte und der
Schrittweite h. Im Falle des Verfahrens von Euler-Cauchy gilt nach einer festen
Integrationszeit T = n · h mit n Schritten f
¨
ur den Fehler
f
t
t
0
t
1
t
2
t
3
t
4
t
5
Bild 1.28: Fl
¨
achenberechnung beim Ver-
fahren von Euler-Cauchy.
x,
ˆx
t
t
0
t
1
t
2
t
3
t
4
t
5
x(t
0
)
ˆx(t
1
)
ˆx(t
2
)
ˆx(t
3
)
ˆx(t
4
)
ˆx(t
5
)
exakter Verlauf x(t)
Bild 1.29: Vergleich zwischen exakter
L
¨
osung x(t) und N
¨
aherungsl
¨
osung ˆx(t
i
).
30 Kapitel 1. Grundlagen nichtlinearer Systeme
ε
n
,
ε
R
,
ε
G
h
h
∗
Gesamtfehler ε
G
Verfahrensfehler ε
n
Rundungsfehler ε
R
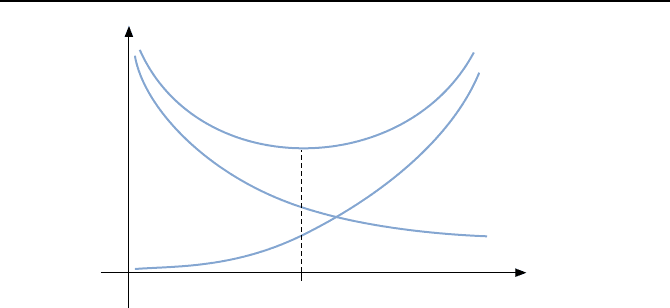
Bild 1.30: Der Gesamtfehler ε
G
eines Integrationsverfahrens setzt sich aus Verfah-
rensfehler ε
n
und Rundungsfehler ε
R
zusammen.
ε
n
≤ α · h.
Der Verfahrensfehler ε
n
nimmt also mit kleiner werdender Schrittweite ab.
Dabei ist im Allgemeinen α eine (leider) unbekannte Konstante.
Bei genaueren Verfahren als dem einfachen Euler-Cauchy-Verfahren kann
der Fehler ε
n
der N
¨
aherungsl
¨
osung bei einer Verringerung der Schrittweite h
auch wesentlich schneller kleiner werden. Allgemein gilt
ε
n
≤ α · h
q
.
Hierbei bezeichnet man q als Fehlerordnung oder Konvergenzordnung des Ver-
fahrens. Sie bestimmt, wie schnell der Fehler ε
n
gegen null konvergiert, wenn
h gegen null strebt. Je gr
¨
oßer q ist, desto genauer ist das L
¨
osungsverfahren.
Bez
¨
uglich der Genauigkeit einer numerischen L
¨
osung von Differenzialglei-
chungen scheint es also sinnvoll zu sein, sehr kleine Schrittweiten h zu w
¨
ahlen.
Allerdings nimmt dann auch die Anzahl ben
¨
otigter St
¨
utzstellen zu, d. h., die
Rechenzeit der Simulation steigt an.
Es gibt einen weiteren Nachteil sehr kleiner Schrittweiten h.Zwarsinktder
Verfahrensfehler ε
n
mit kleiner werdendem h, aber der Rundungsfehler ε
R
des
verwendeten Rechners steigt an. Es existiert also eine optimale Schrittweite
h
∗
, bei der der Gesamtfehler minimal ist. Bild 1.30 illustriert dies. Unprakti-
scherweise ist die optimale Schrittweite h
∗
im Allgemeinen nicht bestimmbar.
1.2.3 Das verbesserte Euler-Cauchy-Verfahren
Das Verfahren von Euler-Cauchy weist aufgrund der gew
¨
ahlten Rechteckn
¨
a-
herung h · f (ˆx
i
,u
i
) eine hohe Ungenauigkeit auf. Man kann das Verfahren
verbessern, wenn man als H
¨
ohe nicht den Wert
f (ˆx(t
i
),u(t
i
))
1.2. L
¨
osung nichtlinearer Differenzialgleichungen 31
f
f (ˆx
i
,u
i
)
t
i
t
i+1
t
F
app
Bild 1.31: Euler-Cauchy-Verfahren.
f
f(ˆx
i+
1
2
,u
i+
1
2
)
t
i
t
i+1
tt
i+1/2
F
app
Bild 1.32: Verbessertes Euler-Cauchy-
Verfahren.
an der Stelle ˆx(t
i
)=ˆx
i
w
¨
ahlt, sondern
f
ˆx
t
i
+
h
2
,u
t
i
+
h
2
an der Stelle ˆx(t
i
+
h
2
)=ˆx
i+1/2
und f
¨
ur u(t
i
+
h
2
)=u
i+1/2
. Die Bilder 1.31
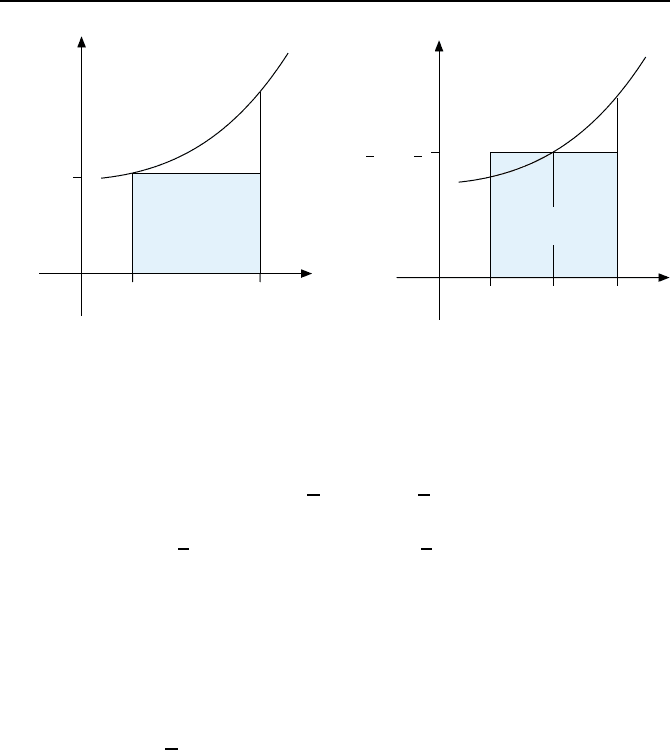
und 1.32 illustrieren den Sachverhalt.
Die Fl
¨
ache des verbesserten Euler-Cauchy-Verfahrens berechnet sich zu
F
app
= h · f
ˆx
i+1/2
,u
i+1/2
.
Man erh
¨
alt so folgenden Algorithmus f
¨
ur das verbesserte Verfahren im allge-
meinen Fall mehrdimensionaler Systemgleichungen:
(1) ˆx
i+1/2
= ˆx
i
+
h
2
· f (ˆx
i
, u
i
),
(2) ˆx
i+1
= ˆx
i
+ h · f
ˆx
i+1/2
, u
i+1/2
.
Das verbesserte Euler-Cauchy-Verfahren heißt auch Halbschrittverfahren.Ge-
gen
¨
uber dem Euler-Cauchy-Verfahren mit der Fehlerordnung q =1besitzt
die verbesserte Version die Fehlerordnung q =2.
1.2.4 Die Verfahren von Heun und Simpson
Weitere Verbesserungen der Genauigkeit gegen
¨
uber den obigen numerischen
L
¨
osungsverfahren lassen sich erzielen, wenn die Fl
¨
ache
F =
t
i+1
t
i
f(x(t),u(t))dt
32 Kapitel 1. Grundlagen nichtlinearer Systeme
f
t
i
t
i+1
t
F
app
Bild 1.33: Verfahren von Heun.
t
t
i
t
i+1
t
i+1/2
f
f
c
2
t
2
+ c
1
t + c
0
F
app
Bild 1.34: Verfahren von Simpson.
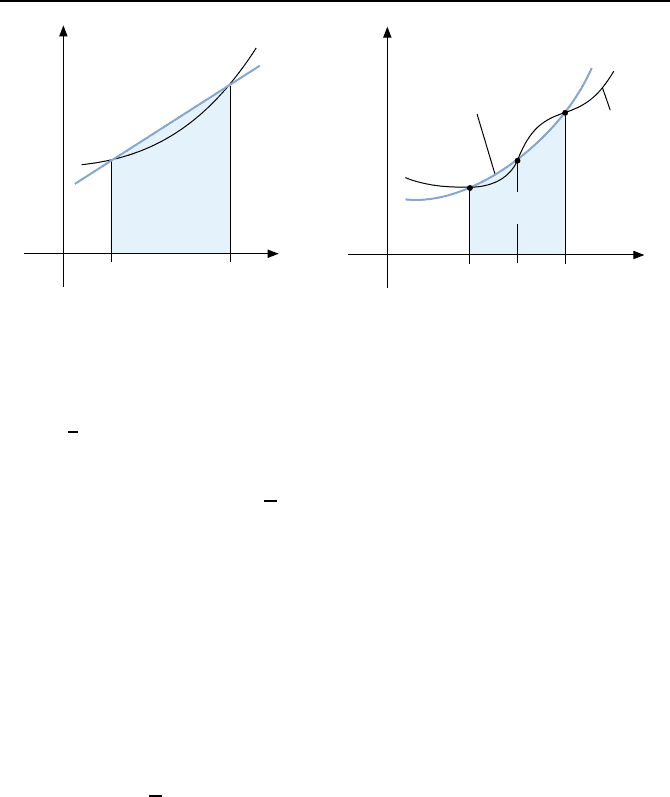
genauer abgesch
¨
atzt wird als mittels eines Rechtecks. Zu diesem Zweck
wird beim Verfahren von Heun ein Trapez f
¨
ur die Berechnung der Fl
¨
ache
F
app
=
h
2
[f(x
i
,u
i
)+f(x
i+1
,u
i+1
)] verwendet, wie in Bild 1.33 illustriert. So-
mit erh
¨
alt man die Rekursionsgleichung
ˆx
i+1
=ˆx
i
+
h
2
[f (ˆx
i
,u
i
)+f (ˆx
i+1
,u
i+1
)].
Hierin ist allerdings ˆx
i+1
auch auf der rechten Seite der Gleichung pr
¨
asent.
Man k
¨
onnte nun diese implizite Gleichung nach ˆx
i+1
iterativ l
¨
osen. Beim
Verfahren von Heun geht man allerdings anders vor und bestimmt ˆx
i+1
n
¨
aherungsweise mittels eines Euler-Cauchy-Schrittes
ˆx
i+1
≈ ˜x
i+1
=ˆx
i
+ h · f (ˆx
i
,u
i
).
Zusammengefasst ergibt sich f
¨
ur den allgemeinen mehrdimensionalen Fall
die Verfahrensvorschrift
(1) ˜x
i+1
= ˆx
i
+ h · f (ˆx
i
, u
i
),
(2) ˆx
i+1
= ˆx
i
+
h
2
[f (ˆx
i
, u
i
)+f (˜x
i+1
, u
i+1
)].
Man bezeichnet das Verfahren von Heun auch als Pr
¨
adiktor-Korrektor-
Verfahren. Hierbei liefert das Ergebnis aus der ersten Gleichung, dem Pr
¨
adik-
tor, eine erste N
¨
aherung. Diese wird mittels der zweiten Gleichung, des Kor-
rektors, nachgebessert.
Zu beachten ist, dass das Verfahren von Heun wie das verbesserte Verfah-
ren von Euler-Cauchy die Fehlerordnung q = 2 aufweist, also keine Erh
¨
ohung
der Genauigkeit erzielt wird.
Verwendet man f
¨
ur die Approximation der Fl
¨
ache
F =
t
i+1
t
i
f(x, u)dt
