J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

64 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Wie auch aus Bild 2.17 abzulesen ist, ergibt sich eine hohe Amplitude der

Schwingung, die nat

urlich f

ur ein Kraftfahrzeug indiskutabel ist. Beseitigt

werden kann der Grenzzyklus durch eine Erweiterung der Regelung [102].

2.2 Absolute Stabilit

2.2.1 Der Begriﬀ der absoluten Stabilit

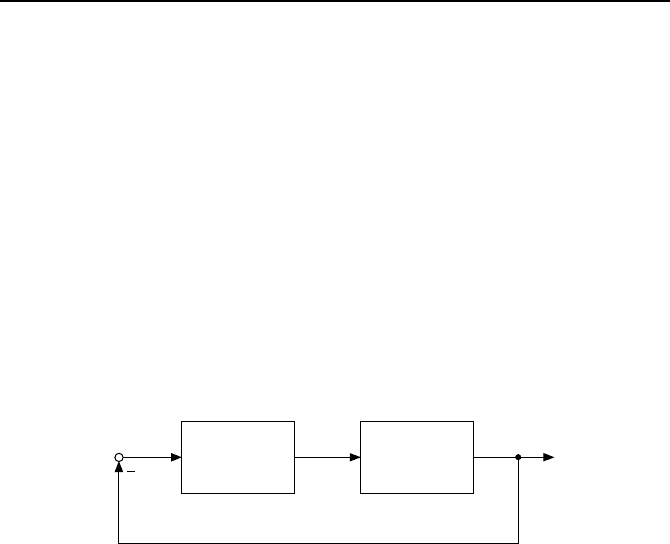
Im vorherigen Kapitel wurde der nichtlineare Standardregelkreis, den Bild

2.18 noch einmal zeigt, auf Grenzzyklen hin untersucht. Es ist nat

urlich auch

von Interesse, wie das Stabilit

atsverhalten geartet ist, wenn keine Grenzzyklen

vorliegen. Beispielsweise ist es von großer praktischer Bedeutung, feststellen

zu k

onnen, f

ur welche Kennlinien f der Regelkreis eine global asymptotisch

stabile Ruhelage besitzt.

u = f (e)

G(s)

Kennlinie

Regelstrecke

Bild 2.18: Nichtlinearer Standardregelkreis.

Dieser Frage soll im Weiteren nachgegangen werden, wobei wir uns auf

Kennlinien beschr

anken, die in einem Sektor liegen, der durch zwei Gera-

den u = K

e und u = K

e begrenzt ist. In Bild 2.19 ist dieser Sektor dar-

gestellt und man bezeichnet ihn kurz, wie es bei Intervallen

ublich ist, mit

]. Passend zu diesem Sektor [K

uhrt man nun einen neuen Sta-

bilit

atsbegriﬀ ein.

Deﬁnition 7 (Absolute Stabilit

at). Der nichtlineare Standardregelkreis

Y (s)=G(s)U(s),

e = −y,

u = f(e)

heißt absolut stabil im Sektor

wenn er f

ur jede eindeutige, st

uckweise stetige und f

ur alle Werte e deﬁnierte

Kennlinie

u = f (e),

die in diesem Sektor liegt, eine global asymptotisch stabile Ruhelage besitzt.

2.2. Absolute Stabilit

at 65

u = K

u = f (e)

Bild 2.19: Kennliniensektor, begrenzt

durch u = K

e und u = K

Hurwitz-Sektor

Sektor absoluter

Stabilit

Bild 2.20: Hurwitz-Sektor und Sektor

absoluter Stabilit

at.

Uber die Gr

oße des Sektors der absoluten Stabilit

at l

asst sich bereits eine

erste Absch

atzung treﬀen. Betrachtet man n

amlich nur lineare Kennlinien

u = f (e)=

K · e,

so kann z. B. mittels des Routh-Kriteriums oder des Wurzelortskurvenverfah-

rens der Parameterbereich

[

] (2.4)

ermittelt werden, f

ur den sich ein stabiler linearer Regelkreis ergibt. Der Sektor

(2.4) heißt Hurwitz-Sektor und oﬀensichtlich ist der Sektor absoluter Stabi-

lit

at immer kleiner oder gleich dem Hurwitz-Sektor. Bild 2.20 illustriert die

Situation.

2.2.2 Das Popov-Kriterium und seine Anwendung

Ein Kriterium zum Nachweis absoluter Stabilit

at wurde 1959 von V. M. Popov

entwickelt [116, 149, 150, 151, 152]. F

ur seine Formulierung muss man zuerst

noch den Begriﬀ der Grenzstabilit

at deﬁnieren.

Deﬁnition 8 (Grenzstabilit

at). Ein lineares System mit der

Ubertragungs-

funktion G(s) heißt grenzstabil, wenn es nur Polstellen p

mit

Re {p

}≤0

besitzt, wobei mindestens f

ur einen Pol Re {p

} =0gilt, und wenn der lineare

Regelkreis

(s)=

G(s)

1+εG(s)

ur jedes beliebig kleine ε>0 stabil ist.

66 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Wurzelortskurve

Bild 2.21: Beispiel f

ur die Wurzelortskurven eines grenzstabilen Systems.

Anschaulich bedeutet die Grenzstabilit

at eines Systems, dass die

Aste der

Wurzelortskurve, die auf der imagin

aren Achse starten, mit wachsendem ε

nach links laufen, wie es Bild 2.21 exemplarisch illustriert.

Popovs Kriterium lautet nun wie folgt.

Satz 1 (Popov-Kriterium). Gegeben sei der nichtlineare Standardregel-

kreis

Y (s)=G(s)U(s),

e = −y,

u = f(e)

mit der stabilen oder grenzstabilen Regelstrecke G(s).DerZ

ahlergrad m von

G(s) sei kleiner als der Nennergrad n. Die Kennlinie u = f(e) sei st

uckweise

stetig, eindeutig, f

ur alle e deﬁniert und gehe durch null. Dann ist der obige

Regelkreis absolut stabil

(1) im Sektor [0,K],wennG(s) stabil ist,

(2) im Sektor [ε, K] mit einem beliebig kleinen ε>0,wennG(s) grenzstabil

ist,

falls sich eine reelle Zahl q ﬁnden l

asst, so dass die Popov-Ungleichung

Re {(1 +

q · jω) · G(jω)} > −

ur alle ω ≥ 0 erf

ullt ist.

Zwei Sachverhalte in diesem Kriterium bed

urfen der Erl

auterung. Zum

einen die Einschr

ankung des Anwendungsbereiches auf Sektoren [0,K]bzw.

[ε, K] und zum anderen die Popov-Ungleichung.

Zuerst soll der Anwendungsbereich n

aher betrachtet werden. Die Unter-

scheidung in die Sektoren [0,K]f

ur stabile G(s) und [ε, K]f

ur grenzstabile

G(s)erkl

art sich daraus, dass eine grenzstabile Strecke G(s) und eine Kenn-

linie

2.2. Absolute Stabilit

at 67

u =0· e

einen Regelkreis ergeben, der nicht global asymptotisch stabil ist. Es bedarf

mindestens einer Verst

arkung ε,also

u = ε · e,

um den Kreis zu stabilisieren.

Die Unterscheidung zwischen den Sektoren [0,K] und [ε, K]hatdesWei-

teren Auswirkungen auf die behandelten Kennlinien u = f(e). So gibt es

Kennlinien, die zwar in [0,K] aber nicht in [ε, K] liegen. Dies ist auch der

Fall, wenn ε>0 beliebig klein sein darf. Zur Erl

auterung betrachten wir zwei

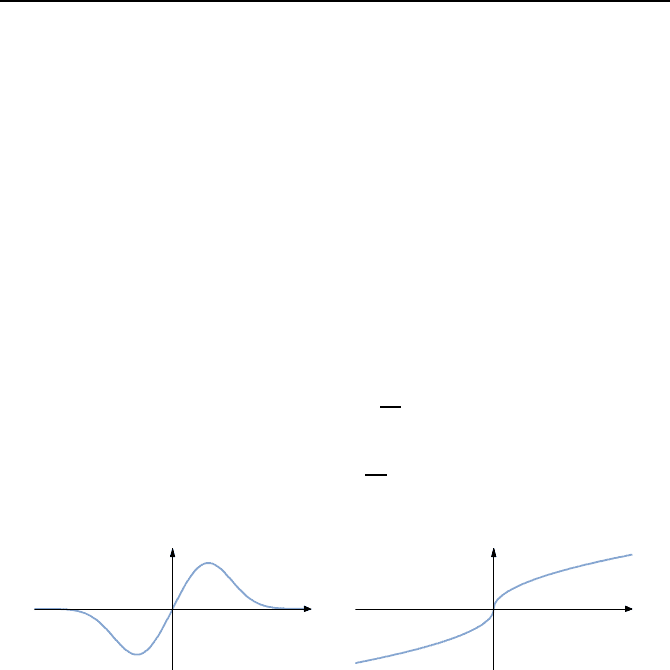
Beispiele. Im ersten, dargestellt in Bild 2.22, strebt die Kennlinie u = f (e)

mit e →∞gegen null, erreicht den Wert null aber nicht. Oﬀensichtlich gibt

es keinen Sektor [ε, K], dessen Gerade u = ε ·e die Kennlinie nicht schneidet.

Im zweiten Beispiel, illustriert in Bild 2.23, strebt

u =sgn(e)



|e|

mit e →∞gegen ∞,jedochschw

acher als irgendeine Gerade u = ε · e.So

wird auch hier die Kennlinie u =sgn(e)



|e| in keinem Sektor [ε, K] liegen.

Bild 2.22: Kennlinie, die f

ur e →∞

gegen null strebt.

Bild 2.23: Kennlinie, die f

ur e →∞

gegen ∞ strebt.

Die Einschr

ankung auf Sektoren [0,K] anstelle [K

] ist nur scheinbar.

Denn durch eine Umformung des betrachteten Regelkreises aus Bild 2.18, bei

dem wir den Sektor [K

]betrachten,l

asst sich erreichen, dass K

= 0 gilt.

Und zwar f

ugt man zwei Faktorglieder mit der Verst

arkung K

, wie in Bild

2.24 gezeigt, in den Regelkreis ein. Ersichtlich heben sich beide Faktorglieder

in ihrer Wirkung auf, so dass man den Regelkreis nicht ver

andert hat. Man

fasst nun die Teilsysteme zusammen und erh

alt den Regelkreis des Bildes 2.25.

Somit hat man f

ur diesen umgeformten Regelkreis als Sektor

− K

]=[0,K = K

− K

]

zu betrachten. Durch diese Transformation k

onnen des Weiteren instabile Re-

gelstrecken stabilisiert werden, so dass das Kriterium von Popov auch auf

solche Regelstrecken anwendbar ist.

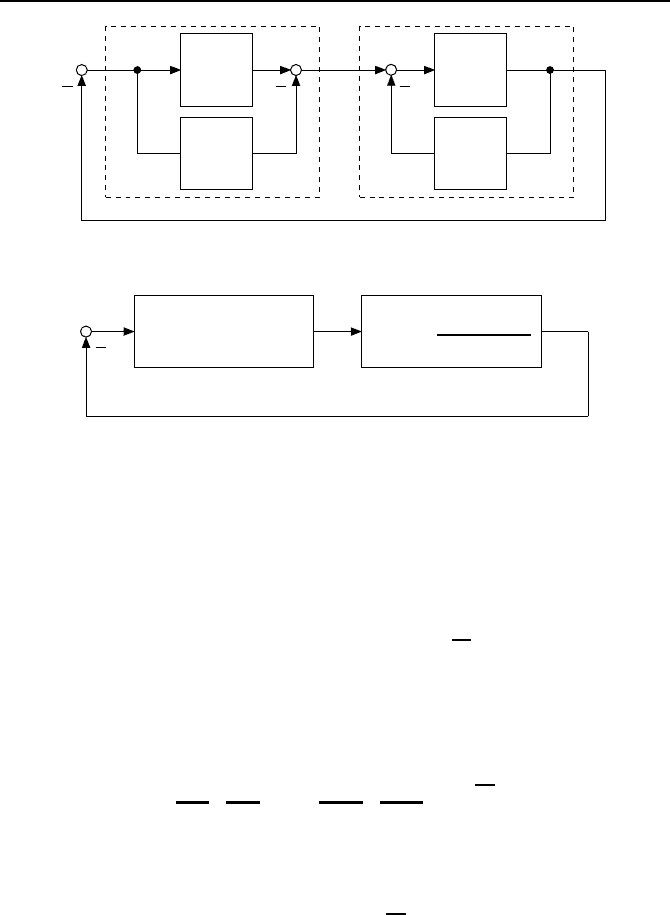
68 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

f(e)

G(s)

Bild 2.24: Einf

ugen eines Faktors K

in den nichtlinearen Standardregelkreis.

f(e)=f(e) −K

G(s)=

G(s)

1+K

G(s)

Bild 2.25: In einen nichtlinearen Standardregelkreis umgeformter Regelkreis aus Bild

2.24.

Nachdem der Anwendungsbereich des Kriteriums von Popov gekl

art ist,

wenden wir uns seiner Anwendung zu. Und zwar ist zu pr

ufen,obsicheine

reelle Zahl q ﬁnden l

asst, so dass die Popov-Ungleichung

Re {(1 + q · jω) ·G(jω)} > −

ur alle ω ≥ 0erf

ullt ist.

Die L

osung der Popov-Ungleichung l

asst sich graﬁsch darstellen. Um das

zu erkennen, formt man sie erst einmal um in

Re {G(jω)}



 

X(ω)

−q · ω Im {G(jω)}



 

Y (ω)

> −

Nun hat man eine in ω parametrierte Ungleichung

X(ω) − q · Y (ω)+

> 0. (2.5)

Sie ist f

ur alle Wertepaare (X, Y ), die rechts der Geraden

X − q · Y +1/K =0

liegen, erf

ullt. Diese Gerade besitzt die Steigung 1/q und den Schnittpunkt

−1/K mit der reellen Achse. Bild 2.26 illustriert dies. Die Gerade wird Popov-

Gerade genannt.

2.2. Absolute Stabilit

at 69

X − qY > −

Steigung

−

Bild 2.26: Sektor (blau), in dem X − qY > −1/K erf

ullt ist.

Allerdings sind nicht alle Werte von X und Y in Gl. (2.5) erlaubt, da sie

uber

X(ω)=Re{G(jω)},

Y (ω)=ω Im {G(jω)}

(2.6)

parametriert sind. Die durch die Gl. (2.6) gegebene Kurve ist in einem Dia-

gramm darstellbar. Sie

ahnelt einer Ortskurve, wenn man

G(jω)=X(ω)+jY (ω)=Re{G(jω)} + jω Im {G(jω)}

setzt. Man bezeichnet diese Ortskurve als Popov-Ortskurve. Sie geht aus der

Ortskurve von G(jω) durch Multiplikation des Imagin

arteils von G(jω)mitω

hervor. Graﬁsch betrachtet wird die Ortskurve G(jω) der Regelstrecke also in

Richtung der imagin

aren Achse ver

andert. Der Realteil dagegen erf

ahrt keine

Ver

anderung. Siehe hierzu Bild 2.27.

Die f

ur X und Y m

oglichen Werte sind also durch Gl. (2.6) gegeben bzw.

liegen auf der Popov-Ortskurve. Damit erh

alt man folgendes graﬁsch darstell-

bares Ergebnis. Die Popov-Ungleichung ist erf

ullt, wenn die Popov-Ortskurve

rechts einer Geraden mit der beliebigen Steigung 1/q und dem Schnittpunkt

−1/K mit der X-Achse, d. h. reellen Achse, liegt.

Mit dem obigen graﬁschen Verfahren ist die Popov-Ungleichung also

osbar. Oﬀensichtlich erf

ullen alle links der Popov-Ortskurve liegenden Gera-

den die Ungleichung. Aus ihnen sind der Wert −1/K und damit die Sektoren

absoluter Stabilit

[0,K]bzw. [ε, K]

direkt ablesbar. Selbstverst

andlich ist man daran interessiert, den gr

oßtm

ogli-

chen Sektor zu bestimmen. Zu diesem Zweck schiebt man die Popov-Gerade so

70 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Popov-

Gerade

Popov-

Ortskurve

beliebige

Steigung

−

G(jω)

ω =1

Bild 2.27: Die Ortskurve, die Popov-

Ortskurve und eine m

ogliche Popov-

Gerade.

kritische

Popov-Gerade

Popov-

Ortskurve

−

Bild 2.28: Die kritische Popov-Gerade

tangiert die Popov-Ortskurve und lie-

fert so den gr

oßten Popov-Sektor.

an die Popov-Ortskurve heran, dass sie diese tangiert und sich das gr

oßtm

ogliche

K = K

ergibt, so wie es Bild 2.28 zeigt. Der zugeh

orige Sektor

[0,K

]

heißt Popov-Sektor. Der Regelkreis ist dann f

ur alle Sektoren

[0,K < K

]bzw. [ε, K < K

]

absolut stabil. F

ur den Popov-Sektor [0,K

] selbst ist absolute Stabilit

durch das Kriterium von Popov nicht nachgewiesen, denn in der Popov-

Ungleichung steht ein Gr

oßer-Zeichen und kein Gr

oßer-gleich-Zeichen. Diese

Unterscheidung ist allerdings in der Praxis nicht von Bedeutung, denn man

wird im Falle einer Realisierung immer einen Sicherheitsabstand zum kriti-

schen Wert K

einhalten.

Angemerkt sei, dass das Popov-Kriterium nat

urlich auch anwendbar ist,

wenn der Regelkreis in der Form

˙x = Ax − bf (c

vorliegt.

Schließlich seien noch zwei Erweiterungen des Popov-Kriteriums aufge-

uhrt. Das Popov-Kriterium ist auch dann anwendbar, wenn G(s)dieForm

G(s)=

G(s) · e

−Ts

hat und

G(s) stabil ist. Allerdings sind dann nur noch positive Werte q in

der Popov-Ungleichung zul

assig und die Nichtlinearit

at muss stetig sein. F

2.2. Absolute Stabilit

at 71

den Fall, dass die Nichtlinearit

at zeitvariant ist, d. h., u = f(e, t) gilt, ist das

Popov-Kriterium ebenfalls anwendbar. Allerdings gelten dann zus

atzlich fol-

gende Einschr

ankungen:

(1) 0 <f(e, t) <Ke,

(2) G(s) besitzt h

ochstens einen Pol s = 0 und ansonsten nur Pole s

mit

Re {s

} < 0 und

(3) q =0.

Die Forderung q = 0 impliziert, dass die Popov-Gerade senkrecht ist.

2.2.3 Aisermans Vermutung

Bei vielen Systemen ist die Anwendung des Popov-Kriteriums unn

otig. Denn

ur sie gilt Aisermans Vermutung, dass der gr

oßte Sektor absoluter Stabilit

dem Hurwitz-Sektor entspricht, der viel einfacher zu bestimmen ist. Wenn

die Vermutung auch im allgemeinen Fall nicht richtig ist, so stimmt sie doch

zumindest f

ur folgende Regelstrecken:

(1) stabile und grenzstabile Systeme erster Ordnung,

(2) stabile und grenzstabile Systeme zweiter Ordnung mit

G(s)=

1+bs

1+a

s + a

bzw. G(s)=

1+bs

1+as

mit jeweils b ≥ 0,

(3) stabile Systeme dritter Ordnung mit

G(s)=

1+bs

1+a

s + a

+ a

,b≥ 0,

oder grenzstabile mit

G(s)=

1+bs

1+a

s + a

,b≥ 0,

(4) Systeme vierter Ordnung ohne Nullstellen mit h

ochstens einem Pol s =0

und sonst nur reellen negativen Polen.

Zumindest f

ur obige Regelstrecken kann man also den gr

oßten Sektor absolu-

ter Stabilit

at durch Bestimmung des Hurwitz-Sektors einfach ermitteln.

Wir betrachten als ein die obigen Betrachtungen erg

anzendes Beispiel die

Regelstrecke

G(s)=

+0.1s + 10)(s

+0.2s + 20)

Im Bild 2.29 sind ihre Ortskurve und Popov-Ortskurve dargestellt, so dass

man den Popov-Sektor zu [0,K

≈ 8.7] ablesen kann. Aus der Ortskurven-

darstellung erkennt man auch, dass der Hurwitz-Sektor mit der maximalen

Steigung K

oßer ist als der Popov-Sektor, denn es gilt

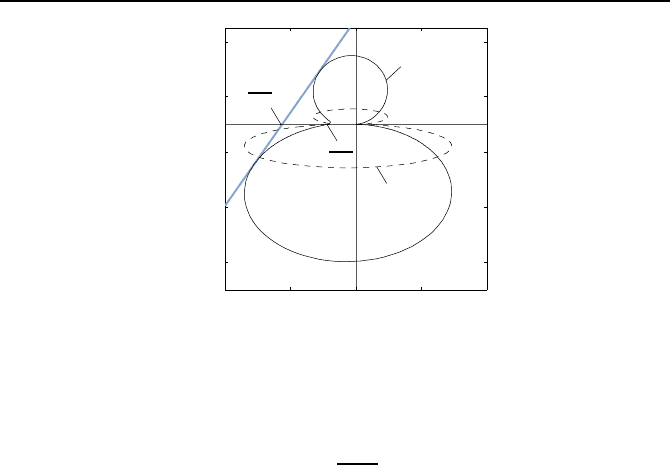
72 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

0.6

0.2

-0.2

-0.6

-1

-0.2

-0.10

0.1

0.2

Popov-

Ortskurve

−

G(jω)

−

Bild 2.29: Beispiel f

ur ein System, bei dem der Hurwitz-Sektor [0,K

]gr

oßer ist als

derPopov-Sektor[0,K

≈ 8.7 <

1012

= K

Aus der Tatsache, dass der Popov-Sektor kleiner ist als der Hurwitz-Sektor,

onnen wir allerdings noch nicht schließen, dass der Sektor absoluter Stabi-

lit

at kleiner ist als der Hurwitz-Sektor. Denn der Beweis [171] des Popov-

Kriteriums sichert nur seinen hinreichenden Charakter und wir wissen nicht,

ob es den gr

oßten Sektor absoluter Stabilit

at geliefert hat. Aisermans Vermu-

tung k

onnte f

ur das obige System also immer noch stimmen. Wie erw

ahnt,

stimmt sie nicht f

ur jedes System [35, 48, 103, 146]. Dies ist aber im Einzelfall

schwer nachzuweisen. Es bleibt folgende generelle Absch

atzung festzuhalten:

Popov-Sektor ≤ gr

oßter Sektor absoluter Stabilit

at ≤ Hurwitz-Sektor.

Mit dem Popov-Kriterium ist Aisermans Vermutung (f

ur bestimmte Re-

gelstrecken) daher nur beweisbar, wenn der Popov-Sektor dem Hurwitz-Sektor

entspricht. Bis heute weder bewiesen noch widerlegt ist, ob der Popov-Sektor

immer gleich dem gr

oßten Sektor absoluter Stabilit

at ist.

2.2.4 Beispiel Schiﬀsregelung

Als Anwendungsbeispiel wird eine Kursregelung des Schiﬀes Tampa der US-

ustenwache betrachtet, das in Bild 2.30 dargestellt ist. Die Regelung soll

so ausgelegt sein, dass bei einer

Anderung des Kurswinkels ϕ von 10

◦

eine

Ausregelzeit von maximal 50 s bei einer Stellgr

oßenbeschr

ankung von ±10

◦

des

Ruderwinkels ϑ erzielt wird. Die Gierrate ˙ϕ wird

uber ein Gyroskop gemessen.

Bild 2.30 illustriert die Aufgabe.

Die

Ubertragungsfunktion G(s) der Tampa zwischen Ruderwinkel ϑ und

Gierrate ˙ϕ wurde experimentell [55] zu

2.2. Absolute Stabilit

at 73

Bild 2.30: Schiﬀ Tampa.

G(s)=

Ω(s)

Θ(s)

−0.0184(s +0.0068)

(s +0.2647)(s +0.0063)

ermittelt, wobei Ω(s) und Θ(s) die Laplace-Transformierten von ω =˙ϕ und

ϑ sind. Geregelt werden soll ϕ. Daher wird die mittels des Gyroskops gemes-

sene Gierrate ˙ϕ zu ϕ auﬁntegriert. Es wird eine Kaskadenregelung mit zwei

P-Reglern f

ur Gierrate und -winkel verwendet. Der I-Anteil der Strecke stellt

sicher, dass es keine bleibende Regelabweichung gibt. Damit der Ruderwinkel

auf ±10

◦

beschr

ankt bleibt, wird ein S

attigungsglied vor die Strecke geschal-

tet. Den Regelkreis zeigt Bild 2.31. Die Regelungen sind so ausgelegt, dass

bei 10

◦

Kurs

anderung die maximal auftretende Stellgr

oße gerade 10

◦

betr

agt.

ur diesen Fall ist der Regelkreis linear. Bei gr

oßeren Kurs

anderungen l

auft

die Stellgr

oße in die S

attigung, d. h., der Kreis wird nichtlinear.

Es stellt sich nun die Frage, ob der Regelkreis auch im nichtlinearen Fall

stabil ist. Um dies mittels des Popov-Kriteriums zu untersuchen, wird der

Regelkreis zun

achst in die Form des nichtlinearen Standardregelkreises um-

geformt. Bild 2.32 zeigt das Ergebnis dieser Umformung. Da die Regelstrecke

einen Integrierer beinhaltet und grenzstabil ist, k

onnen nur Sektoren [ε, K] un-

tersucht werden. Der Sektor [ε, K > 1] schließt jedoch die S

attigungskennlinie

nicht mit ein, da sich ihre Parallele zur Abszisse immer mit jeder beliebigen

Geraden der Steigung ε>0 schneidet. Allerdings geschieht dies f

ur kleine

Werte ε erst bei sehr großen Werten e.DieS

attigungskennlinie liegt also