J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

1.2. L

osung nichtlinearer Diﬀerenzialgleichungen 33

eine Parabel als Interpolationsfunktion f

ur die Funktion f im Intervall [t

i+1

wie in Bild 1.34 dargestellt, so l

asst sich die Genauigkeit weiter steigern.

Wir erhalten dann das Verfahren von Simpson. Um die Parameter der Pa-

rabel zu ermitteln, ben

otigt man neben der St

utzstelle (t

,f(ˆx

)) zwei

weitere St

utzstellen bei t

i+1/2

= t

+ h/2 und t

i+1

sowie den Zwischenwert

i+1/2

= u(t

+ h/2) der Stellgr

oße. Die Integration der Parabel im Intervall

i+1

] liefert dann den Sch

atzwert F

app

ur die zu integrierende Fl

ache.

So ergibt sich das Verfahren von Simpson:

(1) k

= f (ˆx

, u

(2) k

= f



ˆx

, u

i+1/2



(3) k

= f (ˆx

− hk

+2hk

, u

i+1

(4) ˆx

i+1

= x

+4k

+ k

Es besitzt die Fehlerordnung q =3.

1.2.5 Die Runge-Kutta-Verfahren

Die Euler-Cauchy-Verfahren, das Verfahren von Heun und das von Simpson

sind Spezialf

alle der Runge-Kutta-Verfahren. All diese Verfahren bezeichnet

man als Einschrittverfahren, denn sie bestimmen einen neuen Simulations-

punkt ˆx

i+1

nur auf Basis eines vorherigen Punktes ˆx

. Runge-Kutta-Verfahren

haben folgende prinzipielle Form:

(1) k

= f (

, u

(2) k

= f (

+ hα

, u(t

+ β

h)),

(3) k

= f (

+ h (α

+ α

) , u(t

+ β

h)),

(

m) k

= f (

+ h (α

+ ...+ α

m,m−1

m−1

) , u(t

+ β

h)),

(

m +1)

i+1

+ h ·



j=1

Hierbei sind die jeweiligen Fehlerordnungen der Tabelle 1.1 zu entnehmen.

Je mehr Approximationsberechnungen m das gew

ahlte Verfahren ausf

uhrt,

desto genauer ist es. Die Spezialf

alle ergeben sich mit den Parametern m, γ, β,

und α aus Tabelle 1.2.

ur m = 4 gibt es unterschiedliche Varianten, von denen das klassische

Runge-Kutta-Verfahren das gebr

auchlichste ist:

34 Kapitel 1. Grundlagen nichtlinearer Systeme

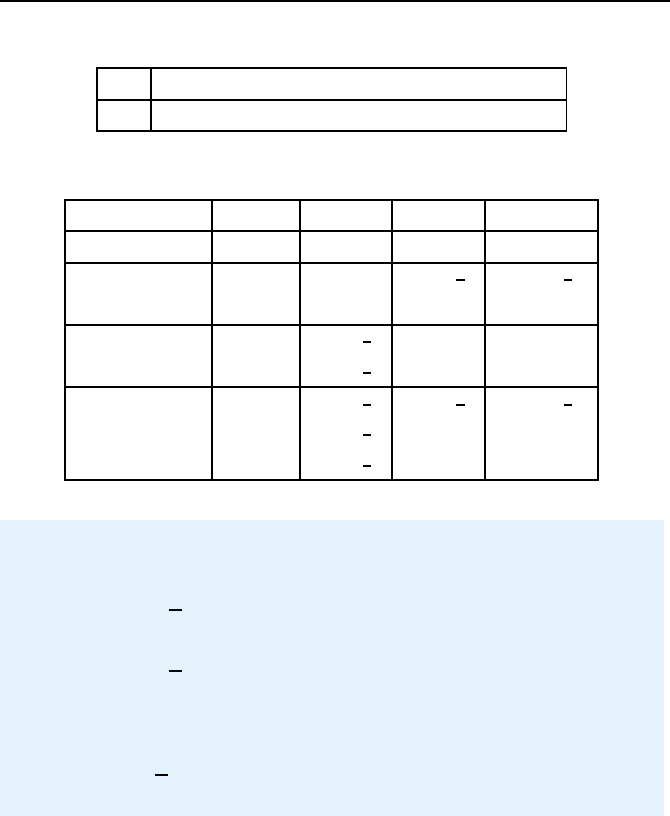
Tabelle 1.1: Fehlerordnungen der Runge-Kutta-Verfahren.

m 123456789

q 123445667

Tabelle 1.2: Spezialf

alle der Runge-Kutta-Verfahren.

m γ β α

Euler-Cauchy m =1 γ

=1 − −

verbessertes m =2 γ

=0 β

Euler Cauchy γ

Heun m =2 γ

=1 α

Simpson m =3 γ

=1 α

= −1

(1) k

= f (ˆx

, u

) ,

(2) k

= f



ˆx

, u

i+1/2



(3) k

= f



ˆx

, u

i+1/2



(4) k

= f (ˆx

+ hk

, u

i+1

) ,

(5) ˆx

i+1

= ˆx

+2k

+ k

) .

Es besitzt die Fehlerordnung q = 4. Runge-Kutta-Verfahren h

oherer Ordnung

ﬁnden sich in [44].

1.2.6 Adaption der Schrittweite

Bisher wurde die Schrittweite h w

ahrend der Rekursion konstant gehalten. Das

ist nicht immer sinnvoll. Besitzt die Diﬀerenzialgleichung Anteile mit stark

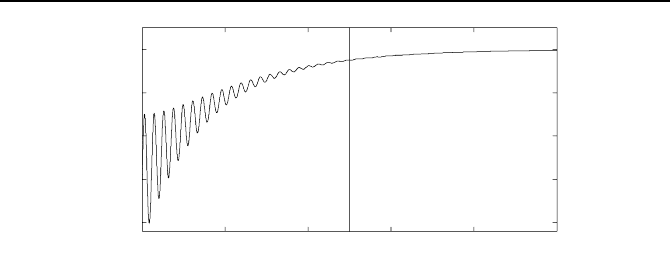
unterschiedlicher Dynamik, wie es Bild 1.35 illustriert, dann f

uhren die bisher

betrachteten Verfahren zu ungenauen oder sehr rechenintensiven L

osungen.

urde man n

amlich eine konstante Schrittweite h w

ahlen, so m

usste sie so

klein gew

ahlt werden, dass der Verlauf im Bereich der Schwingungen (t<5s)

1.2. L

osung nichtlinearer Diﬀerenzialgleichungen 35

x(t)

Zeit t in s

-1

810

Bild 1.35: Diﬀerenzialgleichung mit stark unterschiedlichen Dynamikanteilen.

gut approximiert werden kann. Im schwingungsfreien Kurventeil (t>5s)w

ur-

de die Simulation dann aber unn

otig viele Schritte ausf

uhren, da h hier gr

oßer

gew

ahlt werden k

onnte.

Es ist also sinnvoll, h w

ahrend der Simulation dem L

osungsverlauf ˆx(t)

anzupassen. Man wird f

ur schnelle dynamische Verl

aufe kleine Schrittweiten

ahlen und f

ur langsame große. Mittels einer solchen Schrittweitensteuerung

asst sich dann der Simulationsaufwand und die Simulationsdauer senken.

Eine einfache M

oglichkeit der Schrittweitensteuerung ist folgendes Vor-

gehen, wobei Φ die Verfahrensfunktion, d. h. die Rechenvorschrift f

ur einen

Integrationsschritt, des gew

ahlten L

osungsverfahrens ist und ε ein vorgegebe-

ner Fehler:

Schritt 1: Berechne zwei Rekursionsschritte mit h

ˆx

i+1

= ˆx

+ hΦ(ˆx

, u

,h),

ˆx

i+2

= ˆx

i+1

+ hΦ(ˆx

i+1

, u

i+1

,h).

Schritt 2: Berechne einen Rekursionsschritt mit 2h

˜x

i+2

= ˆx

+2hΦ(ˆx

, u

, 2h).

Schritt 3: Wenn ||ˆx

i+2

− ˜x

i+2

|| >ε, dann setze h

∗

= h/2 und i

∗

= i.

Wenn ||ˆx

i+2

− ˜x

i+2

|| ≤ 0.1ε, dann setze h

∗

=2h und i

∗

= i +2.

Sonst setze

∗

= h und i

∗

= i +2.

Setze i = i

∗

, h = h

∗

, gehe zu Schritt 1 und beginne neu.

Eine wesentlich eﬀektivere Schrittweitensteuerung als obige intuitive ist

die Folgende. Wir w

ahlen zwei Einschrittverfahren und zwar das Verfahren

Γ mit der Fehlerordnung q und das Verfahren Φ mit q +1.Seiε wieder der

36 Kapitel 1. Grundlagen nichtlinearer Systeme

vorgegebene Fehler. Dann gilt folgender Algorithmus:

Schritt 1: Berechne

ˇx

i+1

= ˆx

+ hΓ (ˆx

, u

,h),

˜x

i+1

= ˆx

+ hΦ(ˆx

, u

,h),

S =



h · ε

||ˇx

i+1

− ˜x

i+1



Schritt 2: Wenn S ≥ 1, setze ˆx

i+1

= ˜x

i+1

, h

∗

= h · min{2; S} und i

∗

= i +1.

Wenn S<1, setze h

∗

= h · max{0.5; S} und i

∗

= i.

Setze i = i

∗

, h = h

∗

, gehe zu Schritt 1 und beginne neu.

Insbesondere bei komplexen Systemen, deren Dynamik schwer einsch

atzbar

ist, sollte man immer eine Schrittweitensteuerung verwenden.

1.2.7 Mehrschrittverfahren von Adams-Bashforth

Bisher wurden Einschrittverfahren betrachtet, also Verfahren, bei denen nur

ein vorangegangener Wert ˆx

zur n

aherungsweisen Berechnung der Fl

ache F

und damit von x

i+1

herangezogen wurde. Um die Fl

ache

F =

i+1



f(x(t),u(t))dt

noch genauer zu approximieren als bisher, ist es sinnvoll, ein Interpolations-

polynom f

ur f durch eine Reihe von St

utzstellen

i−k

,f(ˆx

i−k

)) = (t

i−k

i−1

,f(ˆx

i−1

)) = (t

i−1

,f(ˆx

)) = (t

)

und eventuell

i+1

,f(ˆx

i+1

)) = (t

i+1

)

zu legen. Diese letztgenannte St

utzstelle ist gerade die, die man eigentlich

berechnen m

ochte. Sie ist also noch gar nicht bekannt. Bild 1.36 illustriert dies.

Da mehr als eine St

utzstelle f

ur die Fl

achenapproximation verwendet wird,

bezeichnet man entsprechende Integrationsverfahren als Mehrschrittverfahren.

ur den Fall, dass (t

i+1

)nichtalsSt

utzstelle genutzt wird, ergeben

sich die Verfahren von Adams-Bashforth.F

ur den Fall von drei St

utzstellen,

1.2. L

osung nichtlinearer Diﬀerenzialgleichungen 37

i−2

i−1

i+1

i−2

i−1

i+1

Interpolationspolynom

app

Bild 1.36: Adams-Bashforth-Verfahren.

d. h. eines Polynoms dritter Ordnung, erh

alt man das Adams-Bashforth-

Verfahren im allgemeinen Fall zu

ˆx

i+1

= ˆx



55f

− 59f

i−1

+37f

i−2

− 9f

i−3



mit der Fehlerordnung q = 4. Man beachte, dass man die ersten drei Werte

ˆx

, ˆx

und f

, f

ausgehend von ˆx

und f

mittels eines Einschritt-

verfahrens bestimmen muss.

Ein Nachteil der Adams-Bashforth-Verfahren ist die Tatsache, dass das

Interpolationspolynom f

ur die St

utzstellen (t

i−k

),...,(t

), aber nicht

ur (t

i+1

) berechnet wird. Die Approximation von F durch F

app

erfolgt

jedoch im Intervall [t

i+1

]. Da nun Interpolationspolynome außerhalb der

Interpolationsintervalle, hier [t

i−k

], große Fehler aufweisen, wird auch der

Verfahrensfehler in t

i+1

oßer sein als gew

unscht. Um diesen Nachteil der

Adams-Bashforth-Verfahren auszugleichen, verbessern wir sie im Folgenden.

1.2.8 Pr

adiktor-Korrektor-Verfahren von Adams-Moulton

Bei den Verfahren von Adams-Moulton verwendet man ein Adams-Bashforth-

Verfahren als Pr

adiktor und verbessert dessen Ergebnis mittels eines Kor-

rekturterms. Dieser beruht auf einem Interpolationspolynom, das auch die

unbekannte St

utzstelle

i+1

)

nutzt. Man erh

alt so folgende Rekursionsgleichung f

ur ein Interpolationspo-

lynom vierter Ordnung:

ˆx

i+1

=ˆx

720

(251 f(ˆx

i+1

)



 

i+1

+646f

− 264f

i−1

+ 106f

i−2

− 19f

i−3

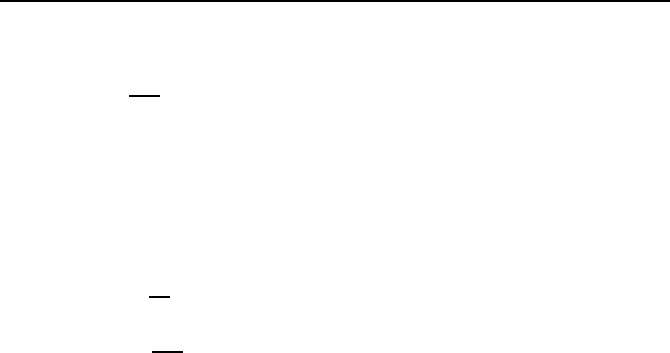
38 Kapitel 1. Grundlagen nichtlinearer Systeme

Diese Gleichung ist implizit in ˆx

i+1

. Man muss also eine Iteration

ˆx

(l+1)

i+1

=ˆx

720

251f(ˆx

(l)

i+1

) + 646f

− 264f

i−1

+ 106f

i−2

− 19f

i−3

durchf

uhren, um ˆx

i+1

zu bestimmen. Und zwar solange bis sich ˆx

(l)

i+1

nicht

mehr wesentlich

andert. Dabei gilt die Regel, dass h mindestens so klein sein

sollte, dass zwei Iterationsschritte l =1, 2 ausreichen.

Zusammengefasst erh

alt man im Mehrgr

oßenfall das Pr

adiktor-Korrektor-

Verfahren von Adams-Moulton mit den zwei Rekursionsgleichungen

(1) ˆx

(0)

i+1

= ˆx



55f

− 59f

i−1

+37f

i−2

− 9f

i−3



(2) ˆx

(l+1)

i+1

= ˆx

720

251f(ˆx

(l)

i+1

, u

i+1

)+646f

−264f

i−1

+106f

i−2

−19f

i−3

und der Fehlerordnung q =5.AuchindiesemFallm

ussen die ersten drei Wer-

te ˆx

nach x

mittels eines Einschrittverfahrens berechnet werden. Dabei ist

es sinnvoll, ein Einschrittverfahren derselben Fehlerordnung q =5zuw

ahlen,

wie sie das obige Mehrschrittverfahren von Adams-Moulton besitzt.

Auch bei Mehrschrittverfahren k

onnen Schrittweitensteuerungen verwen-

det werden. Sie sind allerdings komplexer als im Fall der Einschrittverfahren

[168].

1.2.9 Stabilit

at von Integrationsverfahren

Bei allen Integrationsverfahren stellt sich neben der Frage der Fehlerordnung

q auch die Frage nach ihrer Stabilit

at: Bleibt der Fehler ε

der numerischen

osung beschr

ankt oder steigt er mit zunehmender Schrittzahl und Simula-

tionsdauer unbegrenzt an? Die Antwort h

angt von der Schrittweite h,der

Diﬀerenzialgleichung ˙x = f(x, u) und dem gew

ahlten Integrationsverfahren

ab.

Im allgemeinen Fall l

asst sich obige Frage aufgrund der Nichtlinearit

at von

f nicht exakt beantworten. F

ur den einfachen linearen Testfall

˙x = −λx mit λ>0 (1.24)

und mit dem Anfangswert

x(0) = x

asst sich der Stabilit

atsbereich von h aber berechnen. Da dies f

ur alle be-

trachteten Verfahren m

oglich ist, k

onnen die Verfahren dann bez

uglich ihres

Stabilit

atsverhaltens untereinander verglichen werden und dies erm

oglicht ei-

ne prinzipielle Einsicht in die Verh

altnisse.

Im Falle des Euler-Cauchy-Verfahrens gilt

ˆx

i+1

=ˆx

+ h(−λˆx

)=(1− hλ)ˆx

. (1.25)

1.2. L

osung nichtlinearer Diﬀerenzialgleichungen 39

Oﬀensichtlich ist diese Diﬀerenzengleichung nur dann stabil, wenn

|1 − hλ| < 1, also hλ < 2,

erf

ullt ist. Man gelangt zu diesem Ergebnis auch dann, wenn man ber

ucksich-

tigt, dass das charakteristische Polynom von Gl. (1.25),

P (z)=z − (1 − hλ),

nur Nullstellen innerhalb des Einheitskreises besitzen darf, wenn die Diﬀe-

renzengleichung (1.25) stabil sein soll. F

ur hλ < 2strebtdieL

osung der

Diﬀerenzengleichung (1.25) also gegen denselben Wert wie die L

osung der

Diﬀerenzialgleichung (1.24). Der Verlauf von ˆx

kann dabei allerdings wesent-

lich von x(t) abweichen.

Ahnlich wie f

ur das Euler-Cauchy-Verfahren kann die Stabilit

at f

ur den

betrachteten Testfall ˙x = −λx auch f

ur andere Verfahren untersucht werden.

Es ergeben sich die Stabilit

atswerte hλ aus Tabelle 1.3. Man beachte, dass

hλ > 0 gilt.

Tabelle 1.3: Stabilit

atswerte.

Euler-Cauchy hλ < 2

verbessertes Euler-Cauchy hλ < 2

Heun hλ < 2

Simpson hλ < 2.5359

Runge-Kutta 4. Ordnung hλ < 2.7853

Adams-Bashforth 4. Ordnung hλ < 0.3

Adams-Moulton 5. Ordnung hλ < 1.8367

Das Adams-Bashforth-Verfahren hat einen sehr kleinen Stabilit

atsbereich.

Dieser Sachverhalt ist auf die Interpolation im Intervall [t

i+1

] durch ein

Polynom zur

uckzuf

uhren, das auf den vorherigen St

utzstellen (t

i−k

) ,

...,(t

) beruht. Interpolationspolynome sind aber, wie erw

ahnt, nur zwi-

schen den St

utzstellen der Interpolation genau, außerhalb des Interpolations-

bereiches – hier [t

i+1

] – weichen sie oft deutlich vom zu approximierenden

Verlauf ab. Dadurch wird die Berechnung des Integrals ungenau.

Um das Stabilit

atsverhalten der Verfahren zu illustrieren, sind f

ur den

Testfall ˙x = −λx mit λ = 1 und den Anfangswert x(0) = 1 f

ur verschiedene

Schrittweiten h Simulationen durchgef

uhrt worden und in Bild 1.37 darge-

stellt. Die analytische L

osung dieser Diﬀerenzialgleichung ist x(t)=e

−t

Stabile Schrittweiten h f

uhren, wie vorheriges Beispiel illustriert, nicht

immer zu Verl

aufen mit hinreichend kleinen Simulationsfehlern. F

ur das be-

trachtete Beispiel ˙x = − x zeigt Bild 1.38 den prozentualen Fehler

40 Kapitel 1. Grundlagen nichtlinearer Systeme

x(t)

Zeit t in sZeit t in s

0.50.5

-0.5-0.5

-1-1

6688

1010

−t

h=0.5

h=1

h=2

h=1.5

h=3

h=2.7853

h=2.5

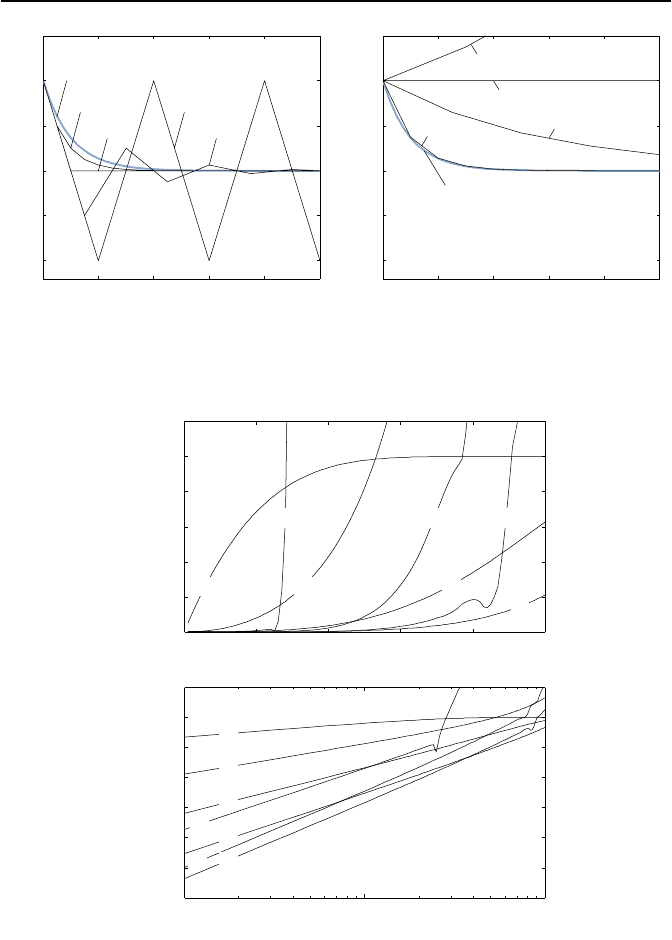
Bild 1.37: L

osung von ˙x = −x mit Euler-Cauchy-Verfahren (links) und klassischem

Runge-Kutta-Verfahren vierter Ordnung (rechts) f

ur verschiedene Schrittweiten h.

100

120

−10

−8

−6

−4

−2

0.2

0.40.60.8

−2

−1

Schrittweite h

relativer Fehler in %

Bild 1.38: Relativer Fehler in linearer Darstellung und in doppeltlogarithmischer

Darstellung f

ur folgende Verfahren: 1. Euler-Cauchy, 2. verbessertes Euler-Cauchy,

3. Simpson, 4. klassisches Runge-Kutta, 5. Adams-Bashforth mit q = 4, 6. Adams-

Moulton mit q = 5 (eine Iteration), 7. Adams-Moulton mit q = 5 (zehn Iterationen).

1.2. L

osung nichtlinearer Diﬀerenzialgleichungen 41

rel

|ε

· 100% =

− ˆx

· 100%

an der Stelle t =10s f

ur verschiedene Schrittweiten h. Die logarithmische Dar-

stellung zeigt hierbei den Fehlerverlauf f

ur kleine Schrittweiten detaillierter als

die linear skalierte Darstellung.

Wie aus Bild 1.38 erkennbar, liefert das klassische Runge-Kutta-Verfahren

vierter Ordnung eine Approximation der L

osung mit niedrigem Fehler bei

vertretbarem Rechenaufwand. Verglichen mit den anderen Verfahren bietet es

einen sehr guten Kompromiss zwischen Genauigkeit und Aufwand. Deshalb ist

es auch das am h

auﬁgsten verwendete Verfahren. Bei kleinen Schrittweiten ist

das Pr

adiktor-Korrektor-Verfahren von Adams-Moulton noch genauer als das

Runge-Kutta-Verfahren. Allerdings ist sein Rechenaufwand deutlich gr

oßer.

1.2.10 Steife Systeme und ihre L

osung

Die bisher betrachteten Einschritt- und Mehrschrittverfahren eignen sich oft

nicht f

ur Systeme

˙x = f (x),

deren Zustandsvariablen x

ein stark unterschiedliches Dynamikverhalten zei-

gen oder die sehr unterschiedliche Dynamikanteile enthalten. Diese Systeme

bezeichnet man als steife Systeme. Ein einfaches lineares Beispiel ist das Sys-

tem

˙x

= −x

˙x

= −100x

Oﬀensichtlich ergibt sich bei der numerischen L

osung das Erfordernis, die

Schrittweite h sokleinzuw

ahlen, dass die zweite Diﬀerenzialgleichung hinrei-

chend genau gel

ost werden kann. Daraus resultiert dann allerdings eine sehr

lange Gesamtsimulationsdauer, da die erste Diﬀerenzialgleichung eine hun-

dertmal l

angere Simulationsdauer ben

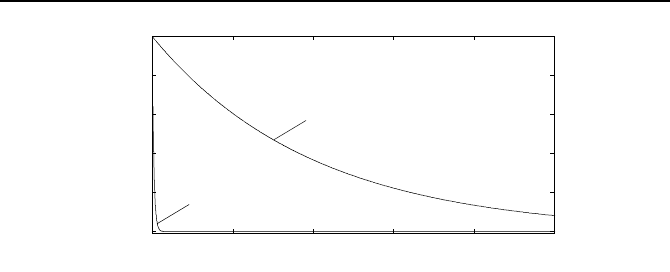
otigt als die zweite. Bild 1.39 illustriert

dies.

Eine L

osungsm

oglichkeit f

ur solche steifen Diﬀerenzialgleichungen sind

Einschrittverfahren mit Schrittweitensteuerung. Diese haben wir im Abschnitt

1.2.6 behandelt. Im Fall von Mehrschrittverfahren setzt man speziell entwi-

ckelte Methoden ein, die auf impliziten Rekursionsformeln basieren und

uber

besonders gute Stabilit

atseigenschaften verf

ugen.

Betrachtet man beispielsweise das Verfahren von Euler, so kann man an-

stelle von

F =

i+1



f(x, u)dt ≈ hf (x

)

42 Kapitel 1. Grundlagen nichtlinearer Systeme

Zeit t in s

0.8

0.6

0.4

0.2

0.5

11.5

2.5

Bild 1.39: Beispiel eines steifen Systems.

auch

F ≈ hf(x

i+1

)

verwenden. Man erh

alt dann als N

aherungsgleichung

ˆx

i+1

=ˆx

+ hf(ˆx

i+1

Ihr impliziter Charakter bedingt, dass sie f

ur jeden Simulationsschritt i mehr-

fach iteriert werden muss. Es ergibt sich, wie bei der Korrektor-Formel des

Adams-Moulton-Verfahrens, eine iterativ zu l

osende Gleichung

ˆx

(l+1)

i+1

=ˆx

+ hf(ˆx

(l)

i+1

Dieses Verfahren bezeichnet man als implizites Euler-Cauchy-Verfahren.Es

ist gleichzeitig auch das einfachste einer ganzen Klasse von L

osungsverfahren

ur steife Diﬀerenzialgleichungen: den Verfahren von Gear . Alle diese Ver-

fahren sind implizite Verfahren. Tabelle 1.4 zeigt die Gear-Formeln bis zur

Fehlerordnung q =4f

ur den mehrdimensionalen Fall. Dabei ist M die Anzahl

der St

utzstellen.

Eine wichtige Eigenschaft der Gear-Verfahren ist ihr großer Stabilit

atsbe-

reich. F

ur das Testbeispiel

˙x = −λx, λ > 0,

gilt f

ur den Stabilit

atsbereich zum Beispiel

hλ < ∞,

d. h., die Verfahren sind f

ur alle h stabil. Auch f

ur Gear-Verfahren und andere

Verfahren zur L

osung steifer Diﬀerenzialgleichungen existieren Schrittweiten-

steuerungen [63, 91]. Ein

Uberblick

uber L

osungsverfahren steifer Diﬀerenzi-

algleichungen ﬁndet sich in [67].