J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

1.2. L

osung nichtlinearer Diﬀerenzialgleichungen 43

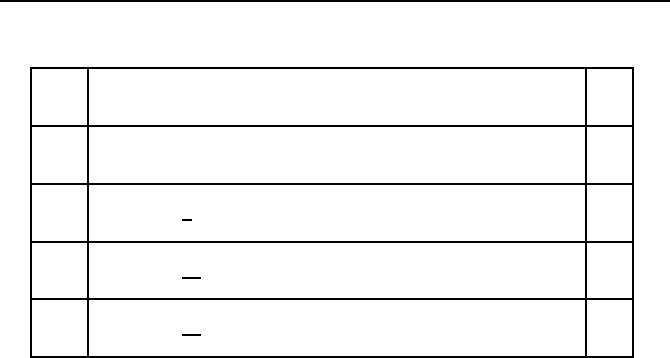
Tabelle 1.4: Gearformeln.

M Gearformeln q

1 ˆx

(l+1)

i+1

= ˆx

+ hf

(l)

i+1

2 ˆx

(l+1)

i+1

“

4ˆx

− ˆx

i−1

+2hf

(l)

i+1

”

3 ˆx

(l+1)

i+1

“

18ˆx

− 9ˆx

i−1

+2ˆx

i−2

+6hf

(l)

i+1

”

4 ˆx

(l+1)

i+1

“

48ˆx

− 36ˆx

i−1

+16ˆx

i−2

− 3ˆx

i−3

+12hf

(l)

i+1

”

Grenzzyklen und Stabilit

atskriterien

2.1 Verfahren der harmonischen Balance

2.1.1 Idee des Verfahrens

Das Verfahren der harmonischen Balance dient dazu, in nichtlinearen Regel-

kreisen, welche die in Bild 2.1 abgebildete Struktur besitzen oder in diese

gebracht wurden, Grenzzyklen aufzusp

uren. Der abgebildete Regelkreis wird

als nichtlinearer Standardregelkreis bezeichnet. Er besteht aus einem linearen

System, das hier durch seine Laplace-

Ubertragungsfunktion G(s) dargestellt

ist und einer nichtlinearen Kennlinie u = f (e), die z. B. als Regler fungiert.

Das Fehlen einer F

uhrungsgr

oße w ist keine große Einschr

ankung, da ei-

ne konstante F

uhrungsgr

oße durch eine Transformation nach null verschoben

werden kann. Außerdem ist ein Grenzzyklus auch f

ur w = 0 auszuschließen.

Es reicht daher aus, den Fall w = 0 zu betrachten.

Nichtlineare Standardregelkreise sind in der Praxis oft anzutreﬀen. Entwe-

der, weil gezielt nichtlineare Regler eingesetzt werden, oder, weil nichtlinea-

re Kennlinien als unerw

unschte Elemente in der Regelkreisstruktur enthalten

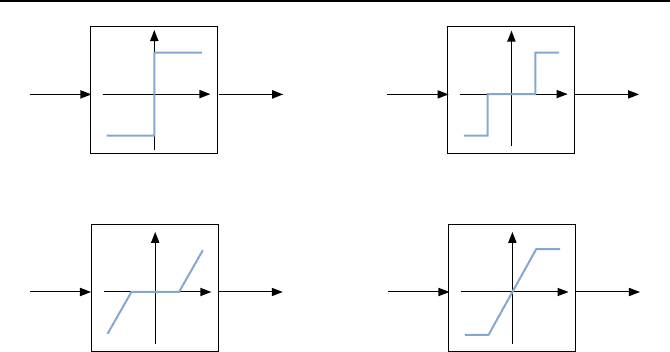
sind, z. B. die Begrenzungskennlinie des Stellgliedes. Typische Kennlinien sind

in Bild 2.2 dargestellt.

Es stellt sich die Frage, wann ein Grenzzyklus in obigem Regelkreis auftre-

ten kann. Um sich an die L

osung dieses Problems heranzutasten, soll zuerst

der Sonderfall einer linearen Kennlinie

nichtlineare Kennlinie lineares System

u = f (e)

G(s)

Bild 2.1: Nichtlinearer Standardregelkreis.

46 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Zweipunktglied

Dreipunktglied

Totzone

(Unempﬁndlichkeitszone)

Begrenzungskennlinie

attigungskennlinie)

Bild 2.2: Typische nichtlineare Kennlinien in Regelkreisen.

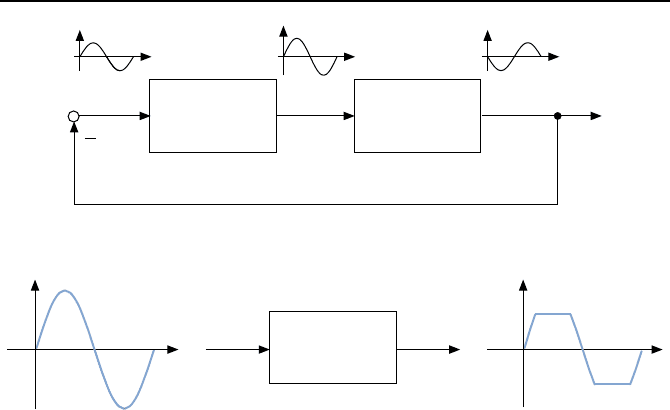
u = f(e)=K · e

betrachtet werden. In diesem Fall hat der Regelkreis die in Bild 2.3 dargestellte

Form. Eine Dauerschwingung, also eine sich selbsterhaltende Schwingung, tritt

gerade dann auf, wenn man in den Regelkreis eine Schwingung

e(t)=A · sin(ω

einspeist und diese um 180

◦

phasenverschoben als

y(t)=A · sin(ω

t − 180

◦

)=−A · sin(ω

am Ausgang des linearen Systems herauskommt. Dann wird die Schwingung

am Summationspunkt erneut in den Regelkreis eingespeist und so weiter. Im

Frequenzbereich lautet obige Bedingung f

ur eine Dauerschwingung

A · e

j(ω

t−180

◦

)

= K ·G(jω

) · A · e

jω

oder

K · G(jω

)=−1. (2.1)

Man bezeichnet dieses Gleichgewicht der Sinusschwingungen am Ein- und

Ausgang des oﬀenen Kreises als harmonische Balance.

Wir k

onnen nun aus obigem Sachverhalt wie folgt auf die nichtlineare

Situation schließen. Schaltet man auf den Eingang der Nichtlinearit

at einen

sinusf

ormigen Signalverlauf

e(t)=A · sin(ω

t),

2.1. Verfahren der harmonischen Balance 47

G(s)

Bild 2.3: Regelkreis mit linearem Regler.

u = f (e)

Bild 2.4: Verzerrung des Eingangssignals durch die Nichtlinearit

at.

so erh

alt man am Ausgang ein verzerrtes Sinussignal, wie es Bild 2.4 exem-

plarisch illustriert.

Das Ausgangssignal u entwickelt man in eine Fourier-Reihe

u(t)=c

(A)+

∞



i=1

(A) · sin(i · ω

t + ϕ

(A)).

Ist nun die Nichtlinearit

at von der Art, dass

(A) = 0 und c

 c

,i=2, 3,...

gilt, also der Gleichanteil null ist und die Amplituden c

der Oberwellen klein

gegen

uber denen der Grundwelle sind, so kann man

u(t) ≈ c

(A) · sin(ω

t + ϕ

(A))

ahern. Die Bedingung c

(A)=0 isterf

ullt, wenn die Kennlinie punktsym-

metrisch ist. Durch obige N

aherung hat man die Nichtlinearit

at f nun lineari-

siert und die lineare N

aherung besitzt eine amplitudenabh

angige Verst

arkung.

Sie ergibt sich aus

e(t)=A · sin(ω

und

u(t)=c

(A) · sin(ω

t + ϕ

(A))

48 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

N(A)=

(A)

· e

jϕ

(A)

Diese Verst

arkung N(A) des linearisierten Kennliniengliedes bezeichnet man

als Beschreibungsfunktion. Man beachte, dass N(A) nicht frequenzabh

angig

ist, Verst

arkungsfaktor c

(A)/A und Phasendrehung ϕ

(A)abervonderAm-

plitude A des Eingangssignals abh

angen.

Das nichtlineare Kennlinienglied wird nun im Regelkreis durch seine linea-

re N

aherung ersetzt, wie in Bild 2.5 gezeigt. F

ur diesen linearen Regelkreis

lautet die bereits hergeleitete Bedingung (2.1) f

ur den Zustand der harmoni-

schen Balance, d. h. eine sich selbsterhaltende Dauerschwingung,

N(A) · G(jω)=−1

oder

G(jω)=−

N(A)

. (2.2)

Obige

Uberlegung ist nat

urlich nur g

ultig, wenn die vernachl

assigten Ober-

wellen mit den Frequenzen 2ω

, 3ω

, 4ω

,... durch die Regelstrecke G(s)aus-

reichend stark ged

ampft werden. D. h., die

Ubertragungsfunktion G(s)muss

ein ausreichend starkes Tiefpassverhalten aufweisen.

Zusammengefasst und auf Kennlinien u = f(e, ˙e) generalisiert erh

alt man

Heuristik 1 (Harmonische Balance). Gegeben sei ein nichtlinearer Stan-

dardregelkreis

Y (s)=G(s)U(s),

e = −y,

u = f(e, ˙e).

Die Kennlinie u = f(e, ˙e) sei punktsymmetrisch bez

uglich des Ursprungs, d. h.,

es gilt f (−e, −˙e)=−f(e, ˙e). Die Regelstrecke besitze einen ausreichend star-

ken Tiefpasscharakter. Existieren dann Werte ω und A, so dass die Gleichung

G(jω)=−

N(A)

erf

ullt ist, so tritt vermutlich eine Dauerschwingung auf, die n

aherungsweise

die Frequenz ω und die Amplitude A besitzt.

Die Beschreibungsfunktion N(A) ist reell, wenn die punktsymmetrische

Nichtlinearit

at nur von e abh

angt. Ist sie auch eine Funktion von ˙e, so besitzt

N(A) in der Regel einen Imagin

arteil.

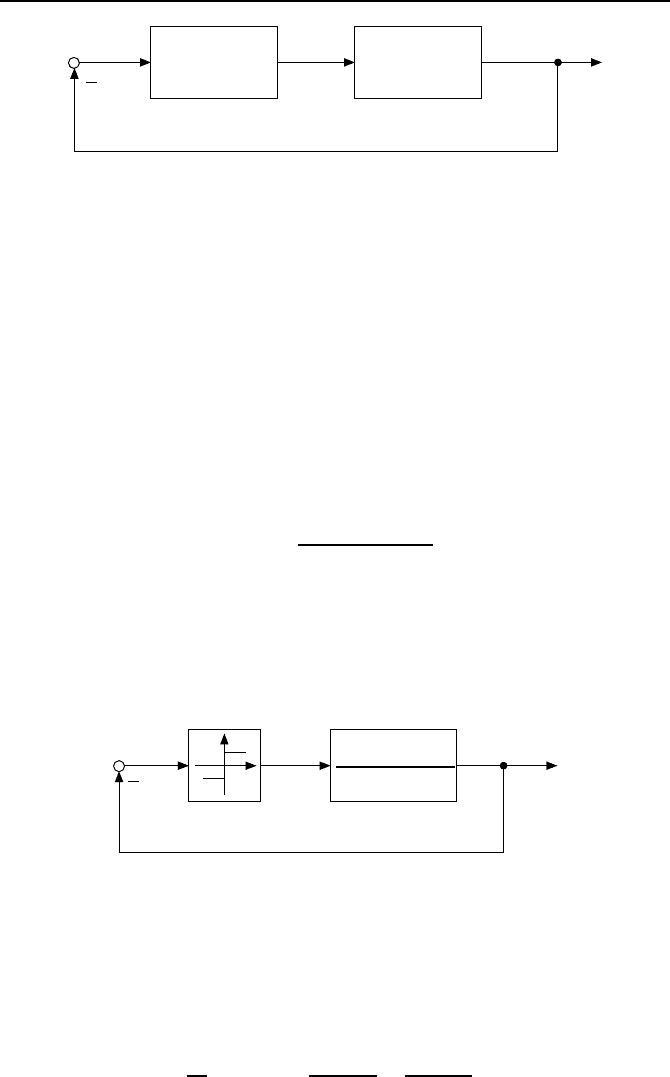
2.1. Verfahren der harmonischen Balance 49

N(A)

G(jω)

Bild 2.5: Linearisiertes Kennlinienglied und lineare Regelstrecke.

Die Bedingung (2.2) l

asst sich graﬁsch auswerten. Zu diesem Zweck zeich-

net man die lineare Ortskurve G(jω) und die Ortskurve −1/N (A)derBe-

schreibungsfunktion. Existiert ein Schnittpunkt, so tritt vermutlich eine Dau-

erschwingung auf. Mittels des Schnittpunktes k

onnen auch die Frequenz und

die Amplitude der vermuteten Dauerschwingung n

aherungsweise berechnet

werden.

2.1.2 Illustrationsbeispiel

Um die oben geschilderte Vorgehensweise zu illustrieren, betrachten wir die

Regelstrecke

G(s)=

s (s +1)(s +9)

die wir mittels eines Zweipunktgliedes

u = −b sgn(y)

regeln. Bild 2.6 zeigt den entsprechenden Regelkreis.

-b

s(s +1)(s +9)

Bild 2.6: Regelkreis mit Zweipunktregler.

Wir ermitteln zuerst die Beschreibungsfunktion N(A) des Zweipunktreg-

lers. Seine Ausgangsfunktion ist f

ur jede Sinusfunktion am Eingang eine Folge

von Rechtecksignalen. Die zugeh

orige Fourier-Reihe der Rechtecksignalfolge

ist

u(t)=



sin ω

t +

sin 3ω

sin 5ω

+ ...



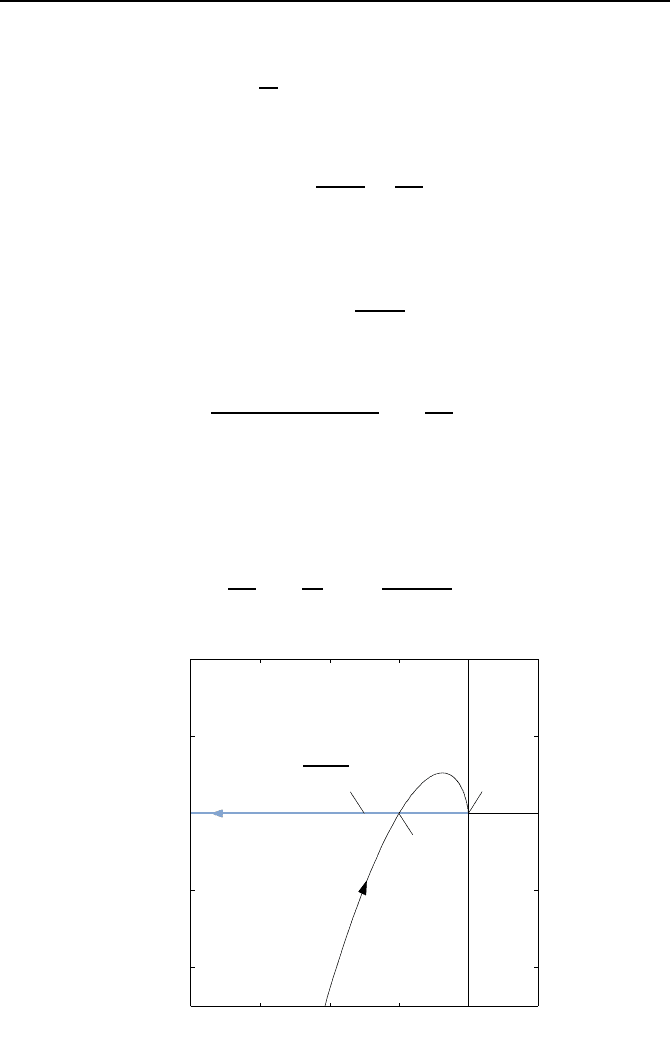
50 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Man n

ahert

u(t) ≈

sin ω

t = c

(A)sinω

und erh

alt

N(A)=

(A)

πA

Um eine Dauerschwingung zu erkennen, stellt man beide Seiten der Glei-

chung der harmonischen Balance

G(jω)=−

N(A)

d. h.

jω(jω +1)(jω +9)

= −

πA

, (2.3)

graﬁsch dar, was in Bild 2.7 geschehen ist. Da ein Schnittpunkt der Ortskurven

G(jω) und −1/N (A) existiert, kann auf eine Dauerschwingung geschlossen

werden. Ihre Amplitude und Frequenz bestimmt man f

ur b = 1 aus Gl. (2.3),

d. h. aus

−

πA

= −

+ j

9ω − ω

Imagin

arteil

Realteil

0.04

0.02

-0.02

-0.04

-0.4-0.3-0.2-0.1

0.1

−

N(A)

A →∞

G(jω)

A =0

Bild 2.7: Verlauf der Ortskurve G(jω) und der Funktion −1/N (A).

2.1. Verfahren der harmonischen Balance 51

ω = 3 und A =

5π

=0.127.

Vergleicht man diese beiden Werte mit den aus einer Simulation ermittel-

ten, so erkennt man den N

aherungscharakter des Verfahrens. Denn aus der

Simulation ergeben sich die Werte ω =2.5 und A =0.195.

2.1.3 Kennlinien und ihre Beschreibungsfunktionen

Das Verfahren der harmonischen Balance ist auch anwendbar, wenn die nicht-

lineare Kennlinie nicht nur von e, sondern auch von ˙e abh

angig ist. Eine der

wichtigsten Kennlinien dieser Art ist die Hysteresekennlinie

u =



b sgn(e + a)f

ur ˙e<0,

b sgn(e − a)f

ur ˙e>0

= b sgn(e − a sgn( ˙e)),

die in Bild 2.8 dargestellt ist. Hysteresekennlinien ﬁnden sich z. B. in Reg-

lern von Temperaturregelkreisen, etwa in B

ugeleisen. Hier wird mittels eines

Bimetalls die Heizung eingeschaltet, bis sich das Bimetall bei einer hohen

Temperatur so verbogen hat, dass es einen Kontakt

oﬀnet und den Heiz-

strom unterbricht. Nach einer Abk

uhlphase hat sich das Bimetall entspannt

und schaltet den Heizstrom wieder ein und so weiter. In elektronischen Bau-

gruppen, wie z. B. analogen Reglerbausteinen, werden Hysteresekennlinien als

Schmitt-Trigger realisiert.

Das Loseverhalten ist eine weitere h

auﬁge Nichtlinearit

at, die außer von e

auch von ˙e abh

angt. Das Loseverhalten wird durch die in Bild 2.9 dargestellte

−a

˙e<0

˙e>0

−b

Bild 2.8: Hysteresekennlinie.

−aa

˙e>0

˙e<0

Steigung m

Bild 2.9: Losekennlinie.

52 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Bild 2.10: Beispielsysteme mit Loseverhalten.

Kennlinie beschrieben. Lose tritt, wie in Bild 2.10 gezeigt, bei mechanischen

Systemen als Spiel zwischen Zahnr

adern, Mitnehmern, Anlenkungen usw. auf.

Man beachte, dass die horizontalen Zweige im Bild 2.9 je nach Vorzeichen von

˙e in beide Richtungen durchlaufen werden. Die horizontalen Zweige k

onnen

ur jeden Wert u auftreten.

Die Beschreibungsfunktion N(A)bestimmtmanauchf

ur Hysteresekenn-

linien und Lose, indem man auf ihren Eingang eine Sinusfunktion schaltet

und das resultierende Ausgangssignal in einer Fourier-Reihe darstellt. Aus

der Grundwelle ergibt sich dann die Beschreibungsfunktion N(A). F

ur Hyste-

rese, Lose und weitere wichtige Kennlinien sind in Tabelle 2.1 die zugeh

origen

Beschreibungsfunktionen N(A) angegeben.

Viele Kennlinien k

onnen additiv aus einigen Standardkennlinien zusam-

mengesetzt werden. Diese Addition von Kennlinien entspricht einer Parallel-

schaltung. Ein Beispiel hierf

ur sind punktsymmetrische Kennlinien in Trep-

penform. Sie k

onnen durch Summation aus Dreipunktkennlinien gebildet wer-

den. Man kann so z. B. die treppenf

ormige Kennlinie eines A/D-Wandlers

nachbilden.

Aufgrund des linearen Charakters von Beschreibungsfunktionen setzt sich

die Beschreibungsfunktion N

ges

(A)vonk parallelgeschalteten Kennlinien

u =



i=1

(e, ˙e)

aus der

Uberlagerung der Beschreibungsfunktion N

(A) der einzelnen Nicht-

linearit

aten f

gem

aß

ges

(A)=



i=1

(A)

zusammen.

2.1. Verfahren der harmonischen Balance 53

Tabelle 2.1: Kennlinien und ihre Beschreibungsfunktionen.

Nichtlinearit

at Beschreibungsfunktion N(A) und Ortskurve −1/N (A)

Zweipunktglied

−b

A →∞

A =0

−

N(A)

N(A)=

πA

,A≥ 0

Vorlast

−b

Steigung: m

A →∞

A =0

−

N(A)

N(A)=

πA

+ m, A ≥ 0

Dreipunktglied

−b

−a

A→∞

A =a

√

A→a

−

πa

−

N(A)

N(A)=

πA

1−

“

”

,A≥ a