J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

1.1. Systembeschreibung und Systemverhalten 13

Ist U(0)=IR

, so bezeichnet man die Ruhelage als global attraktiv . Bild

1.14 illustriert den Begriﬀ der Attraktivit

at. Die Attraktivit

at einer Ruhelage

stellt sicher, dass jede in U(0) startende Trajektorie in die Ruhelage strebt.

Allerdings macht der Begriﬀ der Attraktivit

at keine Aussage dar

uber, wie

weit sich die Trajektorie von der Ruhelage x

= 0 entfernt. Aus praktischer

Sicht heraus betrachtet kann dies problematisch sein. Schließlich m

ochte man

bei realen Systemen auch meistens wissen, welche unter Umst

anden gef

ahrlich

großen Werte der Systemzustand x annehmen kann, bevor er in die Ruhelage

auft. Der nachfolgende Stabilit

atsbegriﬀ ist diesbez

uglich genauer.

Deﬁnition 3 (Stabilit

at im Sinne von Ljapunov). Ein System

˙x = f(x, u)

besitze die Ruhelage x

= 0. Dann heißt die Ruhelage stabil im Sinne von

Ljapunov, wenn es zu jeder ε-Umgebung

(0)={x ∈ IR

||x| <ε}

eine δ-Umgebung

(0)={x ∈ IR

||x| <δ}

gibt, so dass alle Trajektorien des freien Systems, die in der δ-Umgebung

beginnen, d. h.

x(0) ∈ U

(0),

in ihrem weiteren Verlauf in der ε-Umgebung bleiben, d. h.

x(t) ∈ U

(0) f

ur t>0.

Bild 1.15 veranschaulicht die obige Stabilit

atsdeﬁnition von Ljapunov.

Man beachte, dass die Trajektorien x(t) nicht zwingend in die Ruhelage x

laufen m

ussen, damit die Ruhelage stabil im Sinne von Ljapunov ist. Ein kon-

kretes Beispiel hierf

ur ist der harmonische Oszillator

x(t)

U(0)

Bild 1.14: Lokal attraktive Ruhe-

lage.

Bild 1.15: Illustration zur Stabi-

lit

atsdeﬁnition von Ljapunov.

14 Kapitel 1. Grundlagen nichtlinearer Systeme

˙x =



−10



dessen Trajektorien x(t) wir schon in Bild 1.10 sahen.

Ist die Ruhelage x

= 0 attraktiv und stabil im Sinne von Ljapunov, so

streben die Trajektorien aus ihrer Umgebung asymptotisch in die Ruhelage.

Entsprechend deﬁniert man den Begriﬀ der asymptotischen Stabilit

at.

Deﬁnition 4 (Asymptotische Stabilit

at). Ist die Ruhelage x

= 0 lo-

kal (global) attraktiv und stabil im Sinne von Ljapunov, so heißt sie (global)

asymptotisch stabil.

Bei einer asymptotisch stabilen Ruhelage x

sind des Weiteren Umgebun-

gen U(x

) von Interesse, in denen alle Trajektorien in die Ruhelage streben.

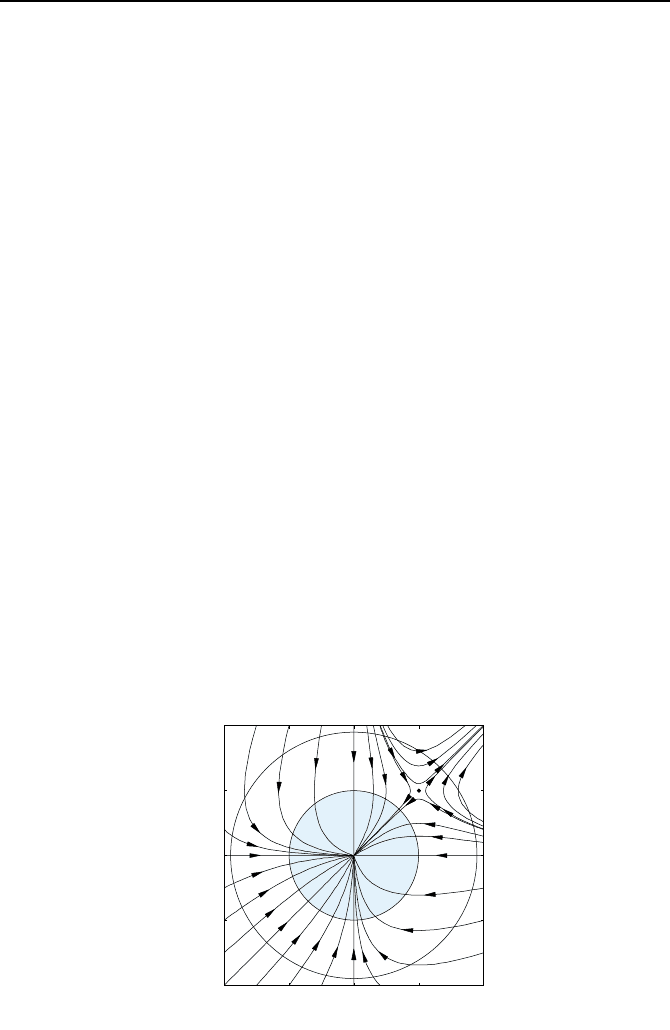
Nicht jede Umgebung besitzt diese Eigenschaft, wie das Beispiel aus Gl. (1.6)

und das zugeh

orige Bild 1.16 veranschaulichen. In der Umgebung U

der Ru-

helage x

= 0 streben alle Trajektorien nach null. In der Umgebung U

ist

dies ersichtlich nicht der Fall.

Man deﬁniert passend zu solchen Situationen den Begriﬀ des Einzugsge-

bietes.

Deﬁnition 5 (Einzugsgebiet). Eine Umgebung einer asymptotisch stabi-

len Ruhelage heißt Einzugsgebiet der Ruhelage, wenn alle in diesem Gebiet

startenden Trajektorien in ihm verbleiben und im weiteren Verlauf in die Ru-

helage streben.

Gibt es nur eine Ruhelage und ist diese global asymptotisch stabil, so ist der

gesamte Zustandsraum Einzugsgebiet. Da das Stabilit

atsverhalten des gesam-

ten Systems in diesem Fall durch diese Ruhelage gekennzeichnet ist, kann dann

auch wie im linearen Fall das System als global asymptotisch stabil bezeichnet

werden.

-2

-1

-2 -1

Zustand x

Bild 1.16: Asymptotisch stabile Ruhelage x

= 0 und ein Einzugsgebiet U

(blau).

Die Umgebung U

ist kein Einzugsgebiet.

1.1. Systembeschreibung und Systemverhalten 15

1.1.7 Grenzzyklen

In nichtlinearen Systemen k

onnen, wie in linearen Systemen, Dauerschwingun-

gen auftreten. Bei diesen Schwingungen wiederholen sich die Systemzust

ande

periodisch und die Trajektorie einer Dauerschwingung ist eine geschlossene

Kurve. Man bezeichnet diese Schwingungen als Grenzzyklen.

Als Beispiel zeigt Bild 1.17 die Dauerschwingung der Van-der-Pol-Diﬀeren-

zialgleichung

˙x

= x

˙x

= −x

+(1− x

Aquivalent zu obigem Zustandsraummodell ist die Diﬀerenzialgleichung

¨x

− (1 − x

)˙x

+ x

=0.

Die Van-der-Pol-Diﬀerenzialgleichung beschreibt z. B. das Verhalten eines

elektrischen Schwingkreises f

ur Radiosender, der aus einer Triode, einem Kon-

densator, einer Spule und einem Widerstand besteht. Der Term (1 −x

)wirkt

dabei als nichtlineares D

ampfungsglied. Man kann einen solchen Van-der-Pol-

Oszillator auch als Regelkreis mit e = −x

als Regelabweichung und mit der

nichtlinearen Kennlinie

u = f (e, ˙e)=−(1 − e

)˙e

als Regelgesetz darstellen. Die lineare Diﬀerenzialgleichung

¨x

+ x

= u

-1

-2

-3

-5

10 20 30 40 -5 5

Zustand x

Zeit t in s

Zustand x

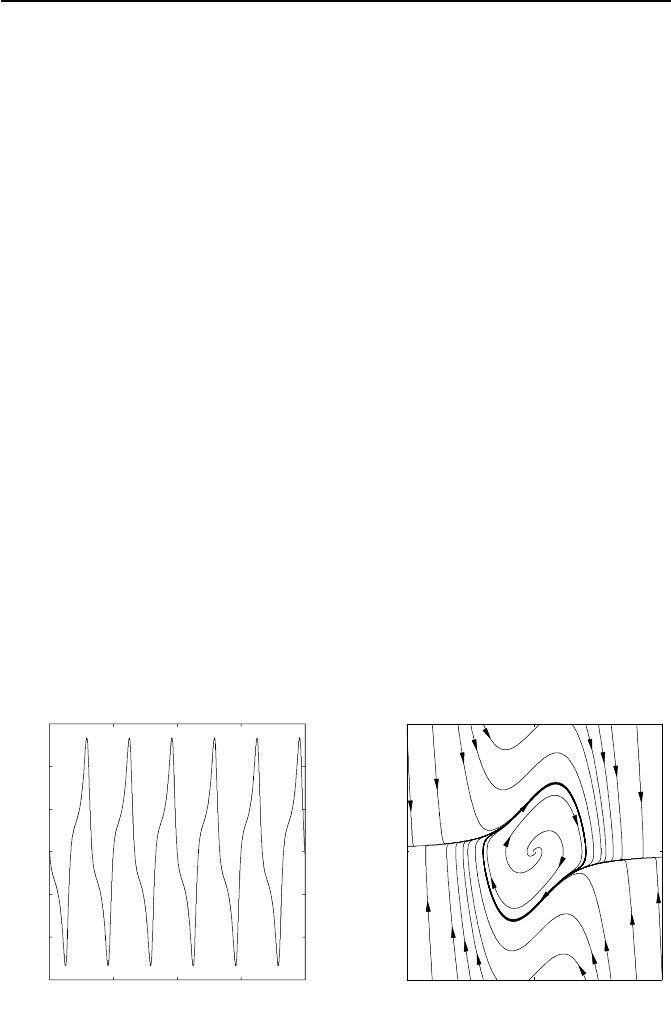
Bild 1.17: Links ist der Zeitverlauf x

(t) und rechts sind die Trajektorien x(t) und

der Grenzzyklus der Van-der-Pol-Diﬀerenzialgleichung dargestellt.

16 Kapitel 1. Grundlagen nichtlinearer Systeme

u = −(1 − e

)˙e

¨x

+ x

= u

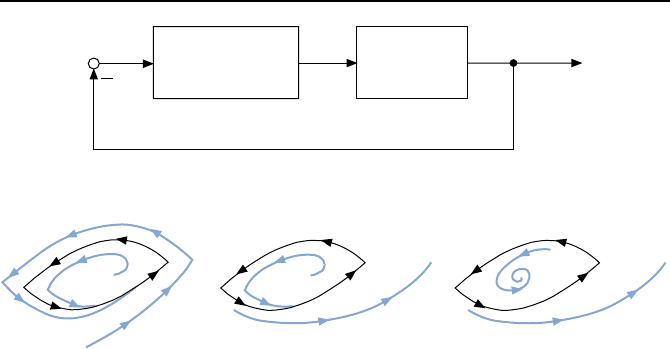
Bild 1.18: Van-der-Pol-Oszillator, dargestellt als Regelkreis.

stabiler Grenzzyklus semistabiler Grenzzyklus instabiler Grenzzyklus

Bild 1.19: Grenzzyklen (schwarz) und ihr Stabilit

atsverhalten.

bildet dann die Regelstrecke, wie in Bild 1.18 dargestellt. Die Aufgabe des

Regelkreises ist in diesem Fall nicht die Ausregelung der Trajektorie in eine

Ruhelage, sondern die Aufrechterhaltung einer Schwingung. Der Grenzzyklus

wird in diesem Beispiel also bewusst erzeugt.

Normalerweise sind Grenzzyklen in Regelkreisen allerdings unerw

unscht.

Denn die Aufgabe eines Regelkreises ist im Allgemeinen das Konstanthalten

der Regelgr

oße und nicht die Erzeugung von Schwingungen.

Ahnlich wie bei Ruhelagen streben Trajektorien entweder in einen Grenz-

zyklus oder von ihm weg. Man kann also den Begriﬀ der Stabilit

at auf Grenz-

zyklen

ubertragen. Drei F

alle sind dabei zu unterscheiden: Im ersten Fall sind

es asymptotisch stabile Grenzzyklen, auf die alle Trajektorien der n

aheren

Umgebung zulaufen. Beim zweiten Fall, dem semistabilen, laufen die Tra-

jektorien von einer Seite auf den Grenzzyklus zu und auf der anderen Seite

von ihm weg. Im dritten Fall entfernen sich alle Trajektorien aus der Um-

gebung des Grenzzyklus, so dass er als instabil bezeichnet wird. Bild 1.19

illustriert diese F

alle. Bei linearen Systemen k

onnen weder stabile, instabile

noch semistabile Grenzzyklen auftreten. Hier sind nur harmonische Oszilla-

toren m

oglich, bei denen es unendlich viele geschlossene Trajektorien gibt.

Keine anderen Trajektorien n

ahern oder entfernen sich von diesen.

Instabile und semistabile Grenzzyklen sind ohne praktische Bedeutung, da

aufgrund kleinster St

orungen – die in einem realen System immer vorhanden

sind – der Grenzzyklus von der Trajektorie verlassen wird. Von regelungstech-

nischer Bedeutung ist also vor allem der stabile Grenzzyklus. Im Allgemeinen

ist er, wie erw

ahnt, unerw

unscht. Um Grenzzyklen in Regelkreisen aufzu-

uren, verwendet man das Verfahren der harmonischen Balance, das wir in

Kapitel 2.1 ausf

uhrlich behandeln.

1.1. Systembeschreibung und Systemverhalten 17

1.1.8 Gleitzust

ande

Außer Grenzzyklen k

onneninnichtlinearenSystemenweitereVerhaltens-

weisen vorkommen, die in linearen Systemen nicht auftreten. Gleitzust

ande

geh

oren zu diesen Ph

anomenen. Sie treten in Systemen mit unstetigem Ver-

halten auf, d. h. in Systemen ˙x = f (x, u) mit unstetigen Funktionen f .

Wir betrachten zur Erkl

arung des Ph

anomens Gleitzustand die Regel-

strecke

˙x =



−2 −3



x +





y =



0.51



die die

Ubertragungsfunktion

G(s)=

s +0.5

(s +1)(s +2)

besitzt. Als Regler verwenden wir einen Zweipunktregler

u =sgn(−y).

Bild 1.20 zeigt den zugeh

origen Regelkreis. Wir simulieren das System f

die Anfangswerte x

(0) = 1 und x

(0) = 1 und erhalten die in Bild 1.21

dargestellten Verl

aufe von Stellgr

oße u und Ausgangsgr

oße y. Oﬀensichtlich

strebt der Ausgangswert y gegen null. Die Stellgr

oße u weist dabei allerdings

ab einem gewissen Punkt keinen konstanten Wert mehr auf, sondern schaltet

hochfrequent zwischen u = 1 und u = −1 hin und her.

-1

s+0.5

(s+1)(s+2)

Bild 1.20: Regelkreis mit Zweipunktregler.

Dieses Verhalten erkl

art sich, wenn man die Trajektorien x(t) des Systems

in der Zustandsebene des Bildes 1.22 betrachtet und das Regelgesetz

u =sgn(−y)=−sgn(0.5x

+ x

)

analysiert. Dieses kann auch in der Form

u =



ur x

< −0.5x

−1f

ur x

> −0.5x

18 Kapitel 1. Grundlagen nichtlinearer Systeme

Stellgr

oße u(t)

Ausgangsgr

oße y(t)

1.5

0.5

-0.5

-1

0.20.20.40.40.60.60.80.8

Zeit t in s

Bild 1.21: Ausgangsgr

oßenverlauf y(t) und Stellgr

oßenverlauf u(t).

Trajektorien x(t)

Zustandsgr

oßen x

(t) und x

(t)

Zustand x

und x

Zeit t in s

0.5

-0.5

-1

1.5

6810-1 -0.50.51

Bild 1.22: Trajektorien x(t) und Gleitzustand auf der (blauen) Schaltgeraden sowie

Zustandsgr

oßenverl

aufe x

(t) und x

(t).

dargestellt werden. Oﬀensichtlich ist unterhalb der Geraden

= −0.5x

(1.7)

der Stellgr

oßenwert u = 1 aktiviert und oberhalb u = −1.

Die Trajektorien x(t) laufen von beiden Seiten auf die Gerade (1.7) zu.

Triﬀt eine Trajektorie auf die Gerade, wechselt sie kurz die Seite, die Stellgr

oße

springt von u =1aufu = −1 oder umgekehrt und die Trajektorie l

auft

wieder auf die Gerade zu. Sie wechselt erneut die Seite und das Spiel beginnt

von vorn. Dadurch tritt das bereits beobachtete hochfrequente Schalten der

Stellgr

oße auf. Die Trajektorie selbst gleitet auf der Schaltgeraden, begleitet

1.1. Systembeschreibung und Systemverhalten 19

vom hochfrequenten Schalten der Stellgr

oße, in die Ruhelage x

= 0.Aus

diesem Gleiten leitet sich auch der Begriﬀ Gleitzustand ab.

Obiges Verhalten hat den Nachteil, dass das Stellglied, z. B. wenn es ein

Ventil oder ein anderer mechanischer Aktor ist, stark belastet wird und schnell

verschleißt. Meistens sind Gleitzust

ande daher unerw

unscht.

Der Gleitzustand hat aber auch einen Vorteil. Das Gleiten der Trajektorie

x(t) in die Ruhelage erfolgt, wie sich zeigen l

asst, robust gegen

uber Parame-

ter

anderungen der Regelstrecke. D. h., der Regelkreis besitzt im Gleitzustand

immer dieselbe Dynamik, auch wenn sich die Regelstrecke ver

andert. Dieses

Verhalten kann daher f

ur den Entwurf einer bestimmten Klasse von robusten

Regelungen, den Gleitzustandsregelungen, ausgenutzt werden. Wir widmen

uns dieser Thematik in Kapitel 5.2.

1.1.9 Chaos

Chaos tritt in biologischen, meteorologischen,

okonomischen und technischen

Systemen auf [21, 95, 180]. Konkrete Beispiele sind Wirtschaftszyklen, Single-

Mode-Laser, mikromechanische Oszillatoren und die Entwicklung von Popu-

lationen in

okologischen Systemen. Die wichtigste Charakteristik chaotischer

Systeme besteht darin, dass man nicht genau sagen kann, wie sich ihre Zu-

standsgr

oßen entwickeln werden. Dies ist insofern erstaunlich, da chaotische

Systeme durch gew

ohnliche Diﬀerenzialgleichungen mit deterministischem

Verhalten beschrieben werden k

onnen. Der Begriﬀ deterministisch schließt da-

bei jegliche Art von stochastischen Einﬂ

ussen auf das System aus. Anschaulich

betrachtet bedeutet chaotisches Verhalten Folgendes:

(1) Die Trajektorien verlaufen aperiodisch, d. h., sie laufen nicht in Grenzzy-

klen hinein.

(2) Die Trajektorien streben weder in eine Ruhelage noch ins Unendliche.

(3) Beliebig nah beieinander liegende Anfangswerte bzw. -vektoren f

uhren zu

sehr unterschiedlichen Trajektorienverl

aufen.

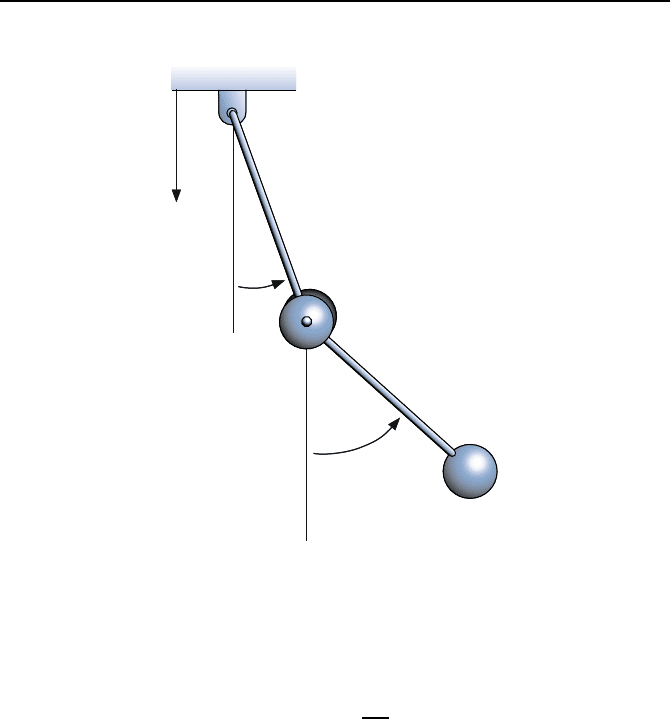
Wir betrachten als Beispiel f

ur ein chaotisches System das Doppelpen-

del, wie es Bild 1.23 zeigt. Die Massen m

und m

angen jeweils an zwei

Pendelst

aben der L

angen l

und l

. Die Gelenke erlauben eine freie Rotation

der Pendel, d. h., die Drehwinkel Θ

und Θ

sind nicht durch Anschl

age be-

schr

ankt. Auf die Pendelmassen wirkt die Erdbeschleunigung g =9.81 m s

−2

so dass das Doppelpendel f

ur die Winkel Θ

= Θ

= 0 eine stabile Ruhelage

besitzt.

Beschrieben wird das System durch die Diﬀerenzialgleichungen

g(sin Θ

cos ΔΘ − μ sin Θ

) − sin ΔΘ(l

+ l

cos ΔΘ)

(μ − cos

ΔΘ)

μg(sin Θ

cos ΔΘ − sin Θ

)+sinΔΘ(μl

+ l

cos ΔΘ)

(μ − cos

ΔΘ)

20 Kapitel 1. Grundlagen nichtlinearer Systeme

Bild 1.23: Doppelpendel mit chaotischem Verhalten.

mit

ΔΘ = Θ

− Θ

μ =1+

Wir simulieren das System f

ur die Parameterwerte m

= m

= 1 kg und

= l

= 1 m. Das chaotische Verhalten des Doppelpendels wird deutlich,

wenn man zwei nah beieinander liegende Anfangsvektoren

⎡

⎢

⎣

(0)

⎤

⎥

⎦

⎡

⎢

⎣

π/2

−π/2

0.01

⎤

⎥

⎦

und

⎡

⎢

⎣

(0)

⎤

⎥

⎦

⎡

⎢

⎣

π/2

−π/2

0.0101

⎤

⎥

⎦

betrachtet und die sich aus ihnen ergebenden Winkelverl

aufe Θ

(t) und

(t)

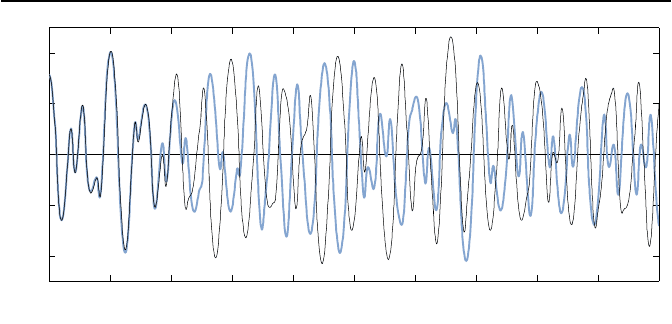
miteinander vergleicht. Wie aus Bild 1.24 erkennbar, verlaufen die Winkel

trotz nahezu identischer Anfangsbedingungen nach einiger Zeit v

ollig unter-

schiedlich und regellos.

Technische Systeme weisen nur sehr selten chaotisches Verhalten auf. Denn

die Entwickler und die Nutzer technischer Systeme sind im Allgemeinen daran

1.1. Systembeschreibung und Systemverhalten 21

in rad

Zeit t in s

-1

-2

10 15 20 25 30 35 40

Bild 1.24: Verl

aufe der Winkel Θ

(schwarze Kurve) und

(blaue Kurve) des

Doppelpendels mit chaotischem Verhalten.

interessiert, dass ihre Anlage, ihr Prozess oder ihr Fahrzeug ein vorhersagba-

res Verhalten besitzt. Im Kapitel 4.4 betrachten wir ein weiteres technisches

chaotisches System, ein Fluidsystem, und regeln es so, dass es eine global

asymptotisch stabile Ruhelage besitzt und folglich kein chaotisches Verhalten

mehr aufweist. Eine detaillierte Darstellung chaotischer Systeme ﬁndet sich

in [6, 7, 34, 174].

1.1.10 Nichtlineare Zustandstransformationen

In der linearen Systemtheorie hat es sich oftmals als sehr n

utzlich erwiesen,

in bestimmten F

allen die Beschreibung

˙x = Ax + Bu (1.8)

eines Systems in eine andere Darstellung zu transformieren. Dies geschieht

mittels einer Koordinatentransformation

x = Tz, (1.9)

wobei der Vektor z die neuen Koordinaten repr

asentiert. Die Matrix T ist

eine regul

are n × n - Matrix. Die neue Systemdarstellung ist dann

˙z = T

−1

AT z + T

−1

Bu. (1.10)

Oftmals w

ahlt man die Transformationsmatrix T so, dass die neue System-

matrix T

−1

AT Diagonalgestalt oder die Gestalt einer Begleitmatrix

−1

AT =

⎡

⎢

⎣

010··· 0

001··· 0

−a

···−a

n−1

⎤

⎥

⎦

22 Kapitel 1. Grundlagen nichtlinearer Systeme

besitzt. Diese Darstellungen sind n

utzlich f

ur den Reglerentwurf oder um Sys-

temeigenschaften aus ihnen direkt ablesen zu k

onnen.

Auch bei nichtlinearen Systemen

˙x = f(x, u) (1.11)

onnen Transformationen

z = q(x)bzw.x = q

−1

(z) (1.12)

sinnvoll sein, wenn es mit ihnen gelingt, das System in eine z. B. f

ur den

Reglerentwurf geeignete Form zu bringen. In der Regel fordert man, dass die

Transformationen (1.12) stetig diﬀerenzierbar und eineindeutig sind. Letzte-

res bedeutet, dass jedem x genau ein z und umgekehrt zugeordnet werden

kann. Eine solche Transformation bezeichnet man als Diﬀeomorphismus.Die

transformierte Beschreibung ergibt sich durch Einsetzen der Transformations-

gleichung (1.12) in die Systembeschreibung (1.11). Wir erhalten so

−1

(z)

= f(q

−1

(z), u),

woraus

∂q

−1

(z)

∂z

· ˙z = f(q

−1

(z), u)

und schließlich die transformierte Systemdarstellung

˙z =



∂q

−1

(z)

∂z



−1

f(q

−1

(z), u)=

f(z, u) (1.13)

folgt. Auf

ahnliche Weise erh

alt man f

ur die R

ucktransformation von z-

Koordinaten in x-Koordinaten die Gleichung

˙x =



∂q(x)

∂x



−1

f(q(x), u)=f(x, u). (1.14)

ur die in Gl. (1.13) verwendete Inverse der Jacobi-Matrix von q

−1

gilt

aufgrund der Ableitungsregel f

ur Umkehrfunktionen



∂q

−1

(z)

∂z



−1

∂q(x)

∂x



x=q

−1

(z)

In vielen F

allen kann die Anwendung obiger Identit

at die Berechnung des

transformierten Systems in Gl. (1.13) erleichtern.

An dieser Stelle wird nun die Forderung nach stetiger Diﬀerenzierbarkeit

von q und q

−1

plausibel. Ist sie erf

ullt, so sind die Matrizen (∂q

−1

(z)/∂z)

−1

und ∂q(x)/∂x stetig. W

are dies nicht der Fall, so w

are es m

oglich, dass die