J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.


104 Kapitel 2. Grenzzyklen und Stabilit
¨
atskriterien
2.4.5 Die indirekte Methode
Die obigen Ergebnisse f
¨
ur zeitkontinuierliche lineare Systeme sind der Aus-
gangspunkt f
¨
ur die Stabilit
¨
atsbetrachtung nichtlinearer Systeme der Form
˙x = Ax + g(x) (2.24)
mit der Ruhelage x
R
= 0.Dabeisollg(x)st
¨
arker gegen x = 0 streben als
|x|. Dies ist der Fall, wenn
lim
|x|→0
g(x)
|x|
= 0
gilt.
Diese Klasse nichtlinearer Systeme (2.24) ist deshalb so interessant, weil
man ein nichtlineares System
˙x = f(x)
in eine Taylor-Reihe entwickeln
˙x = f(x)=f(0)
0
+
∂f
∂x
x=0
A
x + g(x)
und dadurch in die Form (2.24) bringen kann. Es l
¨
asst sich dann mittels
der Ljapunov’schen Stabilit
¨
atstheorie folgender Satz beweisen, den man auch
als Ljapunovs Methode der ersten N
¨
aherung
[2]
oder indirekte Methode von
Ljapunov bezeichnet.
Satz 12 (Indirekte Methode von Ljapunov). Das System
˙x = Ax + g(x)
besitze in x = 0 eine Ruhelage. Es gelte ferner
(1) g(x) ist stetig,
(2) g(x) ist so beschaffen, dass jeder Anfangswert in einer Umgebung von
x = 0 zu einer stetigen, eindeutigen Trajektorie f
¨
uhrt,
(3) lim
|x|→0
g(x)
|x|
= 0.
Ist dann A stabil, so ist die Ruhelage x
R
= 0 asymptotisch stabil. Falls A in-
stabil ist, ist die Ruhelage instabil. Falls A keine Eigenwerte λ
i
mit positivem
Realteil, aber mindestens einen mit Re {λ
i
} =0besitzt, dann ist die Ruhelage
[2]
Die Methode der ersten N
¨
aherung ist nicht identisch mit der hier nicht behan-
delten ersten Methode von Ljapunov. Bei Letzterer basiert die Stabilit
¨
atsanalyse
auf der Kenntnis der Systeml
¨
osungen.
2.4. Die Stabilit
¨
atstheorie von Ljapunov 105
je nach Gestalt von g stabil oder instabil. Ist A stabil, so existiert immer eine
Ljapunov-Funktion
V (x)=x
T
Rx
f
¨
ur ˙x = Ax + g(x), deren Matrix R sich aus
A
T
R + RA = −Q
mit beliebigem positiv definiten Q ergibt.
Der letzte Satz ist von außerordentlicher Bedeutung. Denn er besagt, dass
man das Stabilit
¨
atsverhalten der Ruhelage x
R
= 0 einer großen Klasse nicht-
linearer Systeme anhand der zugeh
¨
origen linearisierten Systeme untersuchen
kann.
2.4.6 Einzugsgebiete
Bisher wurde eine Ruhelage auf ihre Stabilit
¨
at hin untersucht. F
¨
ur die Pra-
xis ist aber nicht nur von Bedeutung, ob eine Ruhelage stabil ist. Sondern
es interessiert uns auch die gr
¨
oßte Umgebung der Ruhelage, in der alle Tra-
jektorien, die in dieser Umgebung beginnen, in die Ruhelage streben. Diese
Umgebung nennt man maximales Einzugsgebiet oder Attraktionsgebiet der
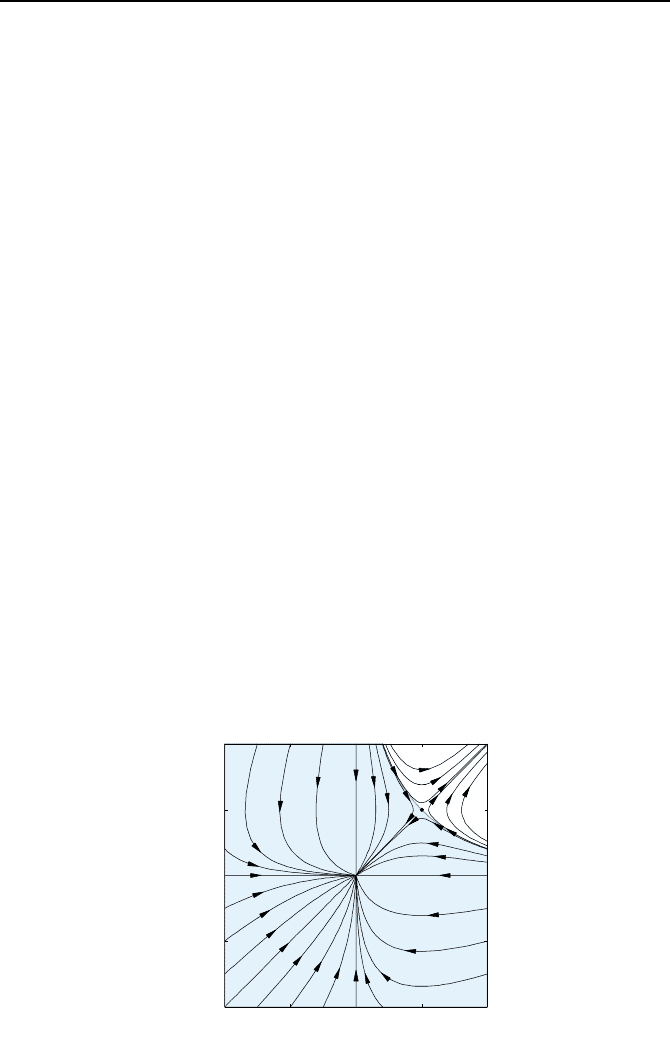
Ruhelage. In Bild 2.64 ist dieses Gebiet f
¨
ur das Beispielsystem aus Abschnitt
2.4.2 skizziert. Die Linie bzw. im H
¨
oherdimensionalen die Fl
¨
ache, die stabile
Trajektorienverl
¨
aufe von instabilen trennt, bezeichnet man als Separatrix.In
Bild 2.64 ist die Separatrix durch den Rand des maximalen Einzugsgebiets
gegeben, der durch die instabile Ruhelage x
R2
=[1 1]
T
verl
¨
auft.
Ist das maximale Einzugsgebiet einer stabilen Ruhelage sehr klein, so ist
die Ruhelage praktisch als instabil anzusehen. Der Nachweis der Stabilit
¨
at
Zustand x
2
Zustand x
1
2
1
0
-1
-2
-2
-1
0
1
2
Bild 2.64: Maximales Einzugsgebiet (blau) des Beispielsystems aus Abschnitt 2.4.2.

106 Kapitel 2. Grenzzyklen und Stabilit
¨
atskriterien
einer Ruhelage ist in der Praxis also nicht ausreichend. Vielmehr muss man
auch die Umgebung der Ruhelage betrachten und das maximale Einzugsgebiet
muss so groß sein, dass alle interessierenden Trajektorien in ihm starten.
Im Allgemeinen kann man das maximale Einzugsgebiet einer Ruhelage
nicht analytisch bestimmen. Es lassen sich aber Teilgebiete des maximalen
Einzugsgebietes ermitteln, wenn man eine Ljapunov-Funktion bestimmt hat.
Ein solches Teilgebiet ist dann ein Einzugsgebiet
[3]
, d. h., alle in ihm starten-
den Trajektorien verlassen das Gebiet nie wieder und streben in die Ruhelage
x
R
= 0. Umgrenzt sind solche Einzugsgebiete z. B. durch die H
¨
ohenlinien
einer Ljapunov-Funktion. Genauer gilt:
Satz 13 (Einzugsgebiet). Ist V (x) eine Ljapunov-Funktion f
¨
ur das System
˙x = f (x) mit der Ruhelage x
R
= 0, dann ist das Gebiet
G = {x ∈ IR
n
| V (x) <c},
falls es beschr
¨
ankt ist, ein Einzugsgebiet der Ruhelage x
R
= 0,wenn
¨
uberall
in G
˙
V (x) < 0
gilt.
Ein Einzugsgebiet G mit den oben genannten Eigenschaften wird gemein-
hin als Ljapunov-Gebiet bezeichnet. Die Forderung
˙
V (x) < 0sichert,dassV
entlang aller Trajektorien abnimmt. Also m
¨
ussen, wie aus Bild 2.61 ersicht-
lich, alle Trajektorien in das Gebiet G laufen. Da auch dort
¨
uberall
˙
V (x) < 0
gilt und G beschr
¨
ankt ist, streben sie auch nach null.
Die Forderung, dass das Gebiet G beschr
¨
ankt sein soll, ist wesentlich. Ist
sie nicht erf
¨
ullt, so ist G nicht zwingend ein Einzugsgebiet, wie folgendes
Beispiel zeigt. Wir betrachten als Ljapunov-Funktion
V (x)=
x
2
1
1+x
2
1
+2x
2
2
. (2.25)
Die Funktion ist nicht unbegrenzt, d. h., es gilt nicht V (x) →∞f
¨
ur |x|→∞,
und somit existieren auch Gebiete
G =
&
x ∈ IR
2
V (x) <c
'
,
die nicht beschr
¨
ankt sind. D. h., die H
¨
ohenlinien sind nicht in jedem Fall ge-
schlossen, sondern laufen f
¨
ur Werte c ≥ 1 ins Unendliche. In Bild 2.65 sind
der Graph und die H
¨
ohenlinien dieser Funktion dargestellt.
Es existieren nun Systeme mit x = 0 als Ruhelage, f
¨
ur die
˙
V (x) < 0
¨
uberall
in IR
n
\{0} gilt und bei denen Trajektorien sich entlang einer H
¨
ohenlinie von
[3]
Im Englischen ist der Begriff contr active (positively) invariant set
¨
ublich. Im Deut-
schen wird dagegen selten der Begriff kontraktive (positiv) invariante Menge ver-
wendet.
2.4. Die Stabilit
¨
atstheorie von Ljapunov 107
Zustand x
1
Zustand x
2
-20 -10
0
10 20
-1.5
-1
-0.5
0
1
0.5
1.5
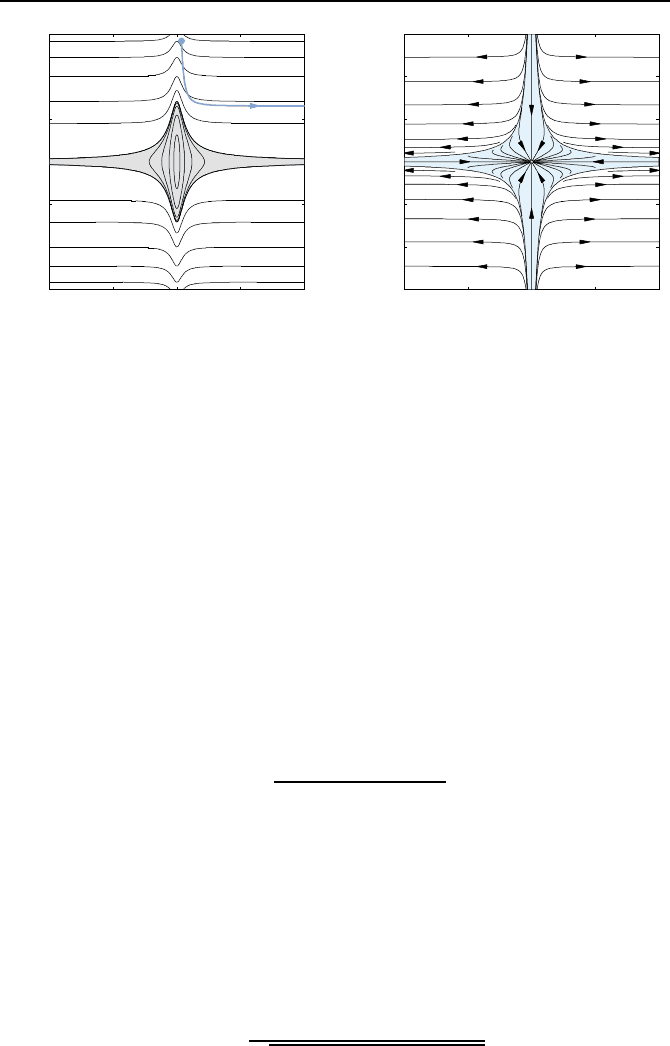
Bild 2.65: H
¨
ohenlinien von V (x). Das
Gebiet mit geschlossenen H
¨
ohenlinien
ist grau, eine instabile Trajektorie des
Systems (2.26) blau dargestellt.
Zustand x
1
Zustand x
2
-20 -10
0
10 20
-1.5
-1
-0.5
0
1
0.5
1.5
Bild 2.66: Trajektorienverl
¨
aufe x(t)
des Systems (2.26). Das Einzugsgebiet
G
max
ist blau dargestellt. Alle Trajekto-
rien außerhalb von G
max
sind instabil.
V (x)mitc>1 ins Unendliche davonstehlen k
¨
onnen, obwohl entlang der Tra-
jektorie ja
˙
V (x) < 0 gilt. Bild 2.65 zeigt eine solche Trajektorie. Offensichtlich
ist G dann kein Einzugsgebiet der Ruhelage x
R
= 0.
Ein solches System [18] ist
˙x
1
= −x
1
+2x
3
1
x
2
2
,
˙x
2
= −x
2
.
(2.26)
Seine Trajektorien zeigt Bild 2.66. F
¨
ur dieses System mit der einzigen Ruhe-
lage x
R
= 0 gilt in der Tat mit der Ljapunov-Funktion (2.25)
˙
V (x)=−
2x
2
1
+4x
2
2
1+2x
2
1
(1 + x
2
1
)
2
< 0
f
¨
ur alle x ∈ IR
2
\{0}. Die Ruhelage x
R
= 0 ist also asymptotisch stabil. Sie
ist aber, wie wir gleich sehen werden, nicht global asymptotisch stabil. Man
beachte, dass Letzteres mit der Ljapunov-Funktion (2.25) auch nicht nach-
weisbar ist, weil sie nicht radial unbeschr
¨
ankt ist. Radiale Unbeschr
¨
anktheit
ist aber eine notwendige Eigenschaft von V f
¨
ur den Nachweis globaler Stabi-
lit
¨
at, wie in Gl. (2.19) gefordert.
Die L
¨
osungen des Systems (2.26) lauten
x
1
(t)=
x
10
e
t
x
2
10
x
2
20
+(1− x
2
10
x
2
20
) e
4t
,
x
2
(t)=x
20
e
−t
(2.27)

108 Kapitel 2. Grenzzyklen und Stabilit
¨
atskriterien
mit x
10
= x
1
(0) und x
20
= x
2
(0). Hieraus ist direkt ersichtlich, dass x(t)
f
¨
ur x
2
10
x
2
20
< 1 stabil in die Ruhelage x
R
= 0 l
¨
auft und f
¨
ur x
2
10
x
2
20
≥ 1ins
Unendliche strebt. Die Anfangswerte, die die Gleichung x
2
10
x
2
20
=1,d.h.
x
20
= ±
1
x
10
,
erf
¨
ullen, bilden die Separatrix. Auf ihr ist die Grenze zwischen stabilen und
instabilen Trajektorien. Die Trajektorien auf der Separatrix selbst sind instabil
und durch
x
1
(t)=x
10
e
t
,
x
2
(t)=x
20
e
−t
gegeben. Im Fall x
2
10
x
2
20
> 1 laufen die Trajektorien in endlicher Zeit ins
Unendliche. Denn der Nenner in Gl. (2.27) wird in diesem Fall f
¨
ur eine endliche
Zeit identisch null und damit x
1
unendlich groß.
Das maximale Einzugsgebiet ist also durch
G
max
=
&
x ∈ IR
2
| x
2
1
x
2
2
< 1
'
gegeben. Bild 2.66 illustriert außer den Trajektorienverl
¨
aufen x(t)auchdas
Gebiet G
max
, dessen Rand die Separatrix des Systems bildet. In Bild 2.65
ist dar
¨
uber hinaus die instabile Trajektorie, die in x
10
= x
20
=1.5startet,
dargestellt. Sie illustriert, wie erw
¨
ahnt, dass V (x) entlang der Trajektorie
abnimmt und diese trotzdem ins Unendliche entschwindet.
2.4.7 Beispiel Mutualismus
Wir betrachten ein dynamisches System aus der
¨
Okologie. In
¨
okologischen Sys-
temen existieren verschiedene, teilweise ganz unterschiedliche Abh
¨
angigkeiten
zwischen den Arten. Am bekanntesten sind R
¨
auber-Beute-Beziehungen, die
oft durch die Lotka-Volterra-Gleichungen modelliert werden. Auch Wechsel-
wirkungen zwischen zwei Arten, bei denen beide Arten Nutzen aus der Be-
ziehung ziehen, werden durch Differenzialgleichungen beschrieben, die eng
mit den Lotka-Volterra-Gleichungen verwandt sind. Solch ein f
¨
ur beide Ar-
ten n
¨
utzliches Zusammenleben bezeichnet man als Mutualismus.
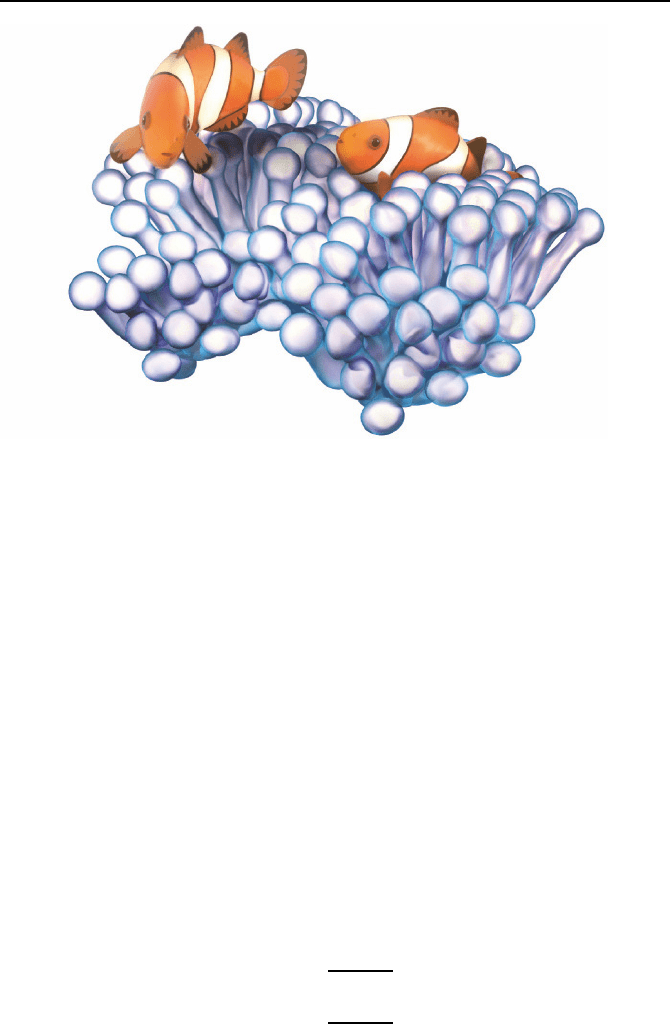
Ein Beispiel hierf
¨
ur ist der in Bild 2.67 dargestellte Mutualismus zwischen
Clownfisch (Amphiprion ocellaris) und Prachtanemone (Heteractis magnifi-
ca). Zum einen sch
¨
utzt die Anemone den Clownfisch mittels ihrer giftigen
Nesselzellen gegen Fressfeinde, zum anderen verteidigt auch der Clownfisch
die Anemone gegen Fressfeinde, z. B. Feilenfische. Ein weiteres Beispiel ist
der Mutualismus zwischen Mensch und Weizen. Modelliert wird ein solcher
Mutualismus durch die Systemgleichungen
˙x
1
= ax
1
− cx
2
1
+ ex
1
x
2
,
˙x
2
= bx
2
− dx
2
2
+ fx
1
x
2
,
(2.28)
2.4. Die Stabilit
¨
atstheorie von Ljapunov 109
Bild 2.67: Mutualismus zwischen Clownfisch und Anemone.
in denen x
1
die Individuenzahl der einen Art und x
2
die der anderen darstellt.
Die Werte a, b, c, d, e und f sind konstante Parameter.
Die Gleichungsanteile ˙x
1
= ax
1
und ˙x
2
= bx
2
in Gl. (2.28) beschreiben li-
neare Wachstumsgesetze, bei denen die Populationen umso st
¨
arker wachsen, je
gr
¨
oßer sie sind. Der Term −cx
2
1
dagegen hemmt das Wachstum der Population
x
1
mit zunehmender Populationsgr
¨
oße, z. B. aufgrund von Nahrungskonkur-
renz innerhalb der eigenen Art. Dies wird auch als intraspezifische Konkurrenz
bezeichnet. Der Term −dx
2
2
hat die gleiche Wirkung. Die Anteile ex
1
x
2
und
fx
1
x
2
bewirken eine gegenseitige F
¨
orderung des Wachstums beider Popula-
tionen. Diese beiden Anteile beschreiben also den Mutualismus innerhalb des
Systems.
Das Modell besitzt die Ruhelagen
x
R1
=
0
0
, x
R2
=
a/c
0
, x
R3
=
0
b/d
.
Ist des Weiteren die Ungleichung ef < cd erf
¨
ullt, so existiert eine vierte Ru-
helage bei
x
R4
=
⎡
⎢
⎢
⎣
be + ad
cd − ef
bc + af
cd − ef
⎤
⎥
⎥
⎦
,
die durch den Mutualismus verursacht wird. F
¨
ur den Fall ef > cd existiert
diese Ruhelage nicht, denn dann ist der Mutualismus viel st
¨
arker als die in-
110 Kapitel 2. Grenzzyklen und Stabilit
¨
atskriterien
traspezifische Konkurrenz und die Populationen x
1
und x
2
wachsen ins Un-
endliche.
Wir betrachten den speziellen Fall
˙x
1
= x
1
− 10
−3
x
2
1
+0.5 · 10
−3
x
1
x
2
,
˙x
2
= x
2
− 10
−3
x
2
2
+0.5 · 10
−3
x
1
x
2
(2.29)
mit den Ruhelagen
x
R1
=
0
0
, x
R2
=
1000
0
, x
R3
=
0
1000
, x
R4
=
2000
2000
.
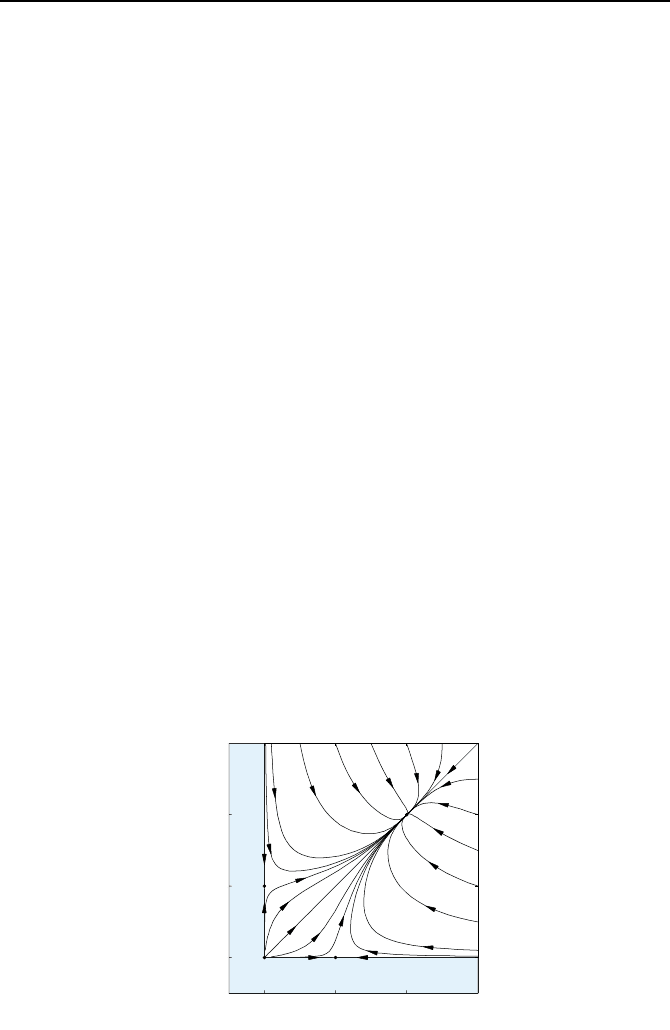
Bild 2.68 zeigt beispielhaft die Trajektorienverl
¨
aufe dieses
¨
okologischen Sys-
tems.
Uns interessiert insbesondere die Ruhelage x
R4
des Mutualismus. Um ihre
Stabilit
¨
at nachzuweisen, transformieren wir x
R4
zuerst mittels
x = z + x
R4
in den Ursprung und erhalten f
¨
ur das System (2.29) nach der Transformation
˙z
1
=(z
1
+ 2000) −10
−3
(z
1
+ 2000)
2
+0.5 · 10
−3
(z
1
+ 2000)(z
2
+ 2000),
˙z
2
=(z
2
+ 2000) −10
−3
(z
2
+ 2000)
2
+0.5 · 10
−3
(z
1
+ 2000)(z
2
+ 2000).
Die Trajektorienverl
¨
aufe des transformierten Systems zeigt Bild 2.69.
Nun setzt man
V (z)=z
2
1
+ z
2
2
als Ljapunov-Funktion an und erh
¨
alt
Zustand x
1
Zustand x
2
0
1000 2000 3000
1000
2000
3000
0
Bild 2.68: Trajektorien des mutualistischen Systems. F
¨
ur negative Individuenzahlen
x
1
und x
2
(blauer Bereich) existieren keine Trajektorien.

2.4. Die Stabilit
¨
atstheorie von Ljapunov 111
˙
V (z)=2z
1
˙z
1
+2z
2
˙z
2
= − 4(z
2
1
+ z
2
2
) − 2 · 10
−3
(z
3
1
+ z
3
2
)+10
−3
z
1
z
2
(z
1
+ z
2
)+4z
1
z
2
.
(2.30)
Um einfach feststellen zu k
¨
onnen, wann
˙
V (z) < 0 gilt, formulieren wir
zwei Polarkoordinaten
z
1
= r cos ϕ,
z
2
= r sin ϕ.
Dabei ist r der Radius und ϕ der Winkel der Polarkoordinaten und r
2
ent-
spricht außerdem dem Niveau einer H
¨
ohenlinie der Ljapunov-Funktion
V (z)=z
2
1
+ z
2
2
= r
2
.
Somit folgt aus Gl. (2.30)
˙
V =−
r
2
(16000 + 5r cos ϕ +3r cos 3ϕ +5r sin ϕ −8000 sin2ϕ − 3r sin 3ϕ)
4000
<0,
was offensichtlich negativ ist, wenn
16000 − 8000 sin2ϕ + r(5 cos ϕ +3cos3ϕ +5sinϕ − 3sin3ϕ) > 0 (2.31)
gilt. Gl. (2.31) ist
¨
aquivalent zur Forderung
1
r
>
3sin3ϕ − 3cos3ϕ − 5cosϕ − 5sinϕ
8000(2 − sin 2ϕ)
,
V(z)=r
2
Zustand z
1
Zustand z
2
-2000 -1000
0
1000
2000
-1000
1000
2000
-2000
0
Bild 2.69: Kreisf
¨
ormiges Einzugsgebiet (blau) der mutualistischen Ruhelage, die hier
nach z = 0 transformiert ist, mit dem Radius r = 1924.

112 Kapitel 2. Grenzzyklen und Stabilit
¨
atskriterien
die sicher erf
¨
ullt ist, wenn
1
r
> max
3sin3ϕ − 3cos3ϕ − 5cosϕ − 5sinϕ
8000(2 − sin 2ϕ)
≈
1
1924
gilt.
F
¨
ur alle Werte r<1924, d. h. innerhalb des Kreises mit dem Radius
r = 1924, ist
˙
V (z) < 0. Die Ruhelage x
R4
ist also stabil und der Kreis mit
r = 1924 und seinem Mittelpunkt in x
R4
ist ein Ljapunov-Gebiet, d. h. ein
Einzugsgebiet. Allerdings bildet dieses Ljapunov-Gebiet, wie aus Bild 2.69 er-
sichtlich, durchaus nicht das maximale Einzugsgebiet. Letzteres besteht aus
der gesamten positiven Zustandsebene. Die Koordinatenachsen geh
¨
oren nicht
zu diesem Einzugsgebiet, da die hier beginnenden Trajektorien in die nicht-
mutualistischen Ruhelagen streben.
2.4.8 Instabilit
¨
atskriterium
Alle betrachteten Methoden zur Stabilit
¨
atsanalyse haben den Nachweis der
Stabilit
¨
at einer Ruhelage zum Ziel. Gelingt der Stabilit
¨
atsnachweis nicht, so
kann das darin begr
¨
undet sein, dass die Stabilit
¨
atsanalysemethode nicht ge-
eignet ist oder die Ruhelage instabil ist. Letzteres ist zwar ein trivialer Grund,
aber oft kein direkt ersichtlicher.
Es kann also sinnvoll sein, eine Ruhelage auf Instabilit
¨
at zu pr
¨
ufen. Im
Prinzip ist das m
¨
oglich, indem man um x
R
= 0 herum
˙
V (x)= ˙x
T
grad V (x) > 0
nachweist. Wir formulieren passend hierzu folgenden Satz, sozusagen als Um-
kehrung des Stabilit
¨
atssatzes von Ljapunov.
Satz 14 (Instabilit
¨
atssatz). Die Differenzialgleichung ˙x = f(x) mit der
Ruhelage x
R
= 0 besitze f
¨
ur jeden Anfangswert aus einer Umgebung U
1
(0) des
Ursprungs eine stetige und eindeutige L
¨
osung. Existiert dann eine Funktion
V (x) mit
(1) V (0)=0,
die in einer Umgebung U
2
(0) ⊆ U
1
(0) stetig ist, stetige partielle Ableitungen
besitzt und dort mit Ausnahme von x = 0 die Bedingungen
(2) V (x) > 0,
(3)
˙
V (x) > 0
erf
¨
ullt, so ist die Ruhelage x
R
= 0 instabil.
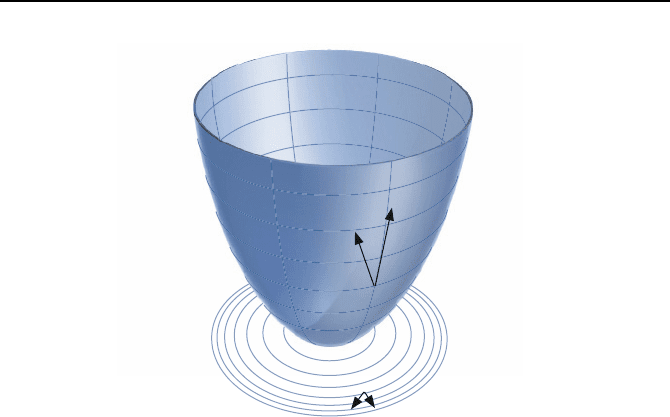
Bild 2.70 illustriert die Aussagen des obige Satzes. Mit diesem Satz kann
man allerdings nicht die Instabilit
¨
at einer Ruhelage nachweisen, wenn es außer
Trajektorien, die von der Ruhelage weglaufen, auch Trajektorien gibt, die in
diese Ruhelage einlaufen. S
¨
atze, die eine entsprechende Untersuchung erlau-
ben, finden sich in der weiterf
¨
uhrenden Literatur [66, 157]. Sie werden in der
Praxis allerdings selten verwendet.
2.4. Die Stabilit
¨
atstheorie von Ljapunov 113
•
•
grad V(x)
˙x
Bild 2.70: Veranschaulichung der Gleichung
˙
V (x)= ˙x
T
grad V (x) > 0.
