J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

84 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Es sei angemerkt, dass diese Deﬁnition auch f

ur nichtlineare Systeme

˙x = f(x, u),

y = g(x, u)

gilt.

In obiger Stabilit

atsdeﬁnition geht x(t) nicht zwingend f

ur t →∞gegen

null. Vielmehr verbleibt die Trajektorie x(t) in einem bestimmten Gebiet. Das

erinnert an die Stabilit

at im Sinne von Ljapunov. Und in der Tat gilt

Satz 5 (Ruhelage eines hyperstabilen Systems). Ist ein lineares System

hyperstabil, so besitzt es eine einzige Ruhelage in

x = 0.

Diese Ruhelage ist stabil im Sinne von Ljapunov.

Man beachte, dass der Begriﬀ der Hyperstabilit

at als Systemeigenschaft

betrachtet wird und nicht als Eigenschaft einer Ruhelage. Das ist m

oglich, da

nur eine Ruhelage existiert und ihre Stabilit

at global ist. In der Praxis wird

man allerdings auch oft

x(t) → 0 f

ur t →∞

fordern. Entsprechend deﬁniert man die asymptotische Hyperstabilit

at wie

folgt.

Deﬁnition 10 (Asymptotische Hyperstabilit

at). Ein hyperstabiles Sys-

tem heißt asymptotisch hyperstabil, wenn f

ur jede Eingangsfunktion u(t),die

die Ungleichung



(τ) · y(τ ) dτ ≤ ε

ur alle t ≥ 0

erf

ullt, f

ur den Zustandsvektor x(t) mit einem beliebigen Anfangsvektor x(0) ∈

lim

t→∞

x(t) → 0

gilt.

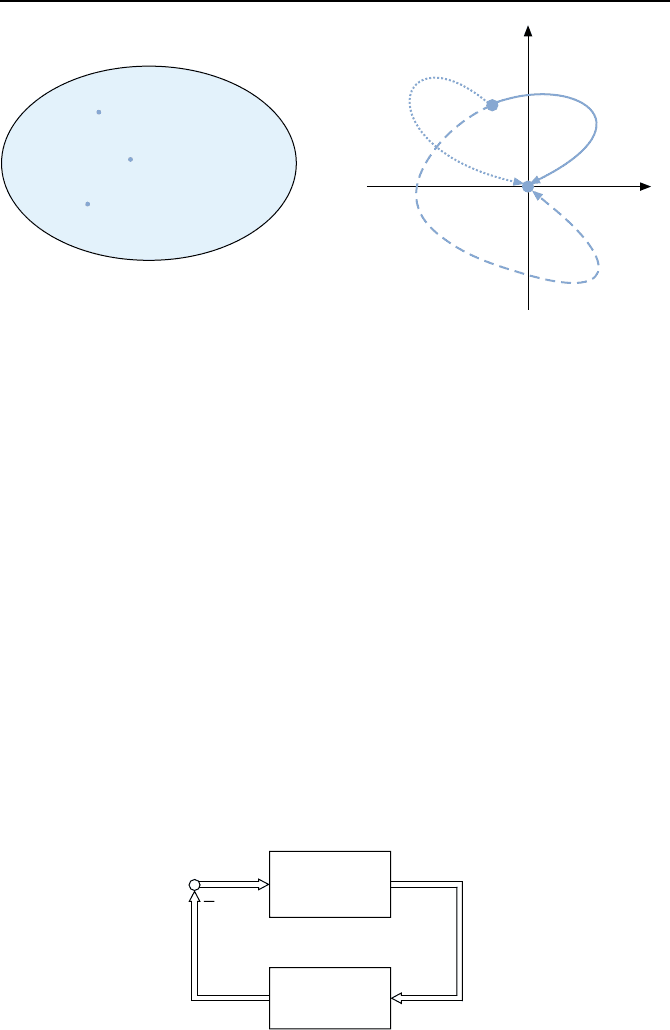
Bild 2.48 illustriert die Deﬁnition anhand dreier Funktionen u

, u

und

aus der Menge der Funktionen, die die Integralungleichung erf

ullen. Die

zugeh

origen Trajektorien x

(t), x

(t) und x

(t) streben asymptotisch in den

Ursprung. Bez

uglich der Stabilit

at der Ruhelage x

= 0 gilt im Fall asymp-

totischer Hyperstabilit

at folgender Satz.

2.3. Hyperstabilit

at 85

(t)

x(0)

(t)

Bild 2.48: Illustrationen zur Deﬁnition 10: Links ist die Menge der erlaubten Funk-

tionen u(t) gezeigt, rechts sind drei Trajektorien x

(t), x

(t) und x

(t) dargestellt,

die aus den Eingangsverl

aufen u

(t), u

(t) und u

(t) resultieren.

Satz 6 (Globale Stabilit

at). Ist ein lineares System asymptotisch hyper-

stabil, so besitzt es die global asymptotisch stabile Ruhelage x

= 0.

Es scheint zun

achst wenig sinnvoll zu sein, obige Deﬁnitionen und S

atze

ur lineare Systeme anzugeben. F

ur sie l

asst sich Stabilit

at nat

urlich einfacher

feststellen. Betrachtet man aber Eingangsfunktionen

u(t)=−F {y(t),t},

die vom Ausgangsvektor y(t)abh

angen, wobei F ein beliebiger Operator sein

kann, so erscheint die Situation in einem neuen Licht: Ein nichtlinearer Re-

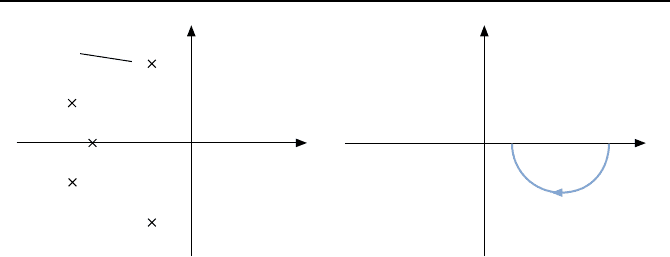
gelkreis wie in Bild 2.49 liegt vor.

Der Operator F kann z. B. eine nichtlineare zeitvariante Funktion

u(t)=−f(y,t)

oder eine Faltungsoperation

G(s)

F {y,t}

Bild 2.49: Nichtlinearer MIMO-Regelkreis mit linearer Regelstrecke und nichtlinea-

rer R

uckf

uhrung.

86 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

u(t)=−



g(t − τ)y(τ) dτ

sein. Die Einhaltung der Integralungleichung



(τ) · y(τ ) dτ ≤ ε

ur alle t ≥ 0

kann dann direkt anhand der Nichtlinearit

u(t)=−v(t)=−F {y,t}

des Regelkreises

uberpr

uft werden. Im Regelkreis des Bildes 2.49 ist also fest-

zustellen, ob



(τ) · y(τ) dτ ≥−ε

ur alle t ≥ 0 (2.10)

gilt. Gl. (2.10) wird als Popov’sche Integralungleichung bezeichnet.

2.3.2 Hyperstabilit

at nichtlinearer SISO-Regelkreise

Bez

uglich der nichtlinearen R

uckf

uhrung betrachtet man als wichtiges Beispiel

ein SISO-System und alle Kennlinien im Sektor [0, ∞), welcher in Bild 2.50

dargestellt ist. Oﬀensichtlich gilt f

ur alle Kennlinien in [0, ∞) die Ungleichung

v · y ≥ 0

bzw.

u · y ≤ 0.

−u, v

Bild 2.50: Kennliniensektor [0, ∞), in dem alle Kennlinien die Popov’sche Integral-

ungleichung erf

ullen.

2.3. Hyperstabilit

at 87

Pole

(a)

Ortskurve

ω = ∞

ω =0

(b)

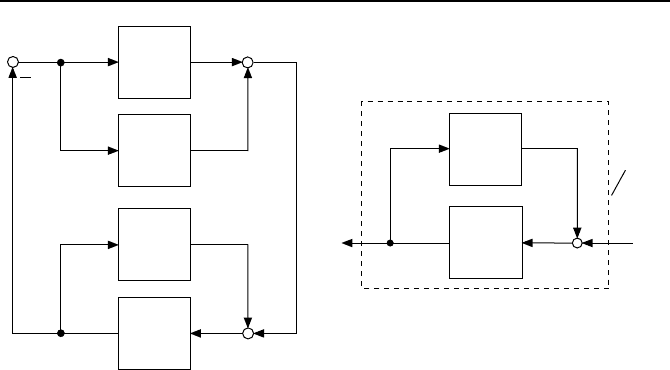
Bild 2.51: Die beiden Bedingungen f

ur die asymptotische Hyperstabilit

at linearer

SISO-Systeme: (a) f

ur alle Eigenwerte gilt Re {λ

} < 0, (b) f

ur die Frequenzen

ω ≥ 0 gilt Re {G(jω)} > 0.

Also ist die Popov’sche Integralungleichung



vy dτ ≥−ε

ur alle t ≥ 0

erf

ullt. An diesem Beispiel erkennt man auch die Verwandtschaft zum Begriﬀ

der absoluten Stabilit

at.

Der Nachweis, dass die nichtlineare R

uckf

uhrung die Popov’sche Integral-

ungleichung erf

ullt, reicht allerdings noch nicht aus, um sicherzustellen, dass

der betrachtete nichtlineare Regelkreis stabil ist. Man hat n

amlich noch zu

uberpr

ufen, ob die lineare Regelstrecke hyperstabil ist. Da man in der Praxis

meistens an einer asymptotischen Ruhelage x

= 0 interessiert ist, wird im

Weiteren nur der Fall der asymptotischen Hyperstabilit

at betrachtet.

Es l

asst sich nun zeigen, dass steuer- und beobachtbare, zeitinvariante

SISO-Systeme

G(s)=d + c

(sI − A)

−1

genau dann asymptotisch hyperstabil sind, wenn die

Ubertragungsfunktion

G(s) stabil ist und Re {G(jω)} > 0f

ur alle ω ≥ 0 gilt. Diese Bedingung

illustriert Bild 2.51. Eine

Ubertragungsfunktion G(s), die beide Forderungen

erf

ullt, nennt man streng positiv reell.

Es gilt f

ur den Regelkreis des Bildes 2.49 im SISO-Fall folgender wichtiger

Stabilit

atssatz.

Satz 7 (Hyperstabilit

at von SISO-Regelkreisen). Gegeben sei der nicht-

lineare Regelkreis

Y (s)=G(s) · U (s),

u = −v,

v = F {y,t}

88 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

mit der steuer- und beobachtbaren, zeitinvarianten Regelstrecke G(s).Erf

ullt

die lineare Regelstrecke die Bedingungen

(1) G(s) ist stabil und

(2) Re {G(jω)} > 0 f

ur alle ω ≥ 0

und erf

ullt die nichtlineare R

uckf

uhrung die Popov’sche Integralungleichung

(3)



v(τ)y(τ) dτ ≥−ε

ur alle t ≥ 0,

dann und nur dann ist der Regelkreis asymptotisch hyperstabil.

In den meisten praktischen F

allen wird die Bedingung (2) des obigen Satzes

nicht erf

ullt sein. Man kann aber auch diesen Fall behandeln, indem man die

Ortskurve soweit nach rechts verschiebt, bis G(s) vollst

andig in der rechten

Halbebene liegt. Bild 2.52 illustriert dies. Dies ist m

oglich, indem man

d als

unstlichen Durchgriﬀ zur Streckenbeschreibung gem

aß

G(s)=

d + G(s)

addiert. Damit dabei der Regelkreis in seinem Verhalten unver

andert bleibt,

muss man den k

unstlichen Durchgriﬀ der Strecke durch eine R

uckkopplung

bei der Nichtlinearit

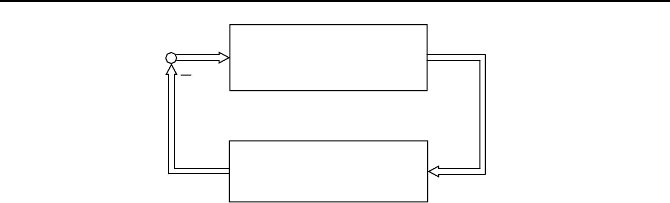
at wieder aufheben. Bild 2.53 zeigt im Teilbild (a) den

entsprechenden Regelkreis und die neue Nichtlinearit

at im Teilbild (b), die

durch den k

unstlichen Durchgriﬀ entstanden ist.

Man hat nun die nichtlineare R

uckf

uhrung

v = F {ˆy + v

d, t} (2.11)

zu untersuchen. Es entsteht also eine neue Nichtlinearit

at, die in die Po-

pov’sche Integralungleichung einzusetzen ist. Leider ist die nichtlineare Funk-

tion (2.11) implizit in v.F

ur die Auswertung der Popov’schen Integralglei-

chung ben

otigen wir den Zusammenhang zwischen v und ˜y aber im Allgemei-

nen in expliziter Form. Leider l

asst sich Gl. (2.11) nicht in jedem Fall in eine

explizite Form bringen. Die Auswertung der Popov’schen Integralgleichung

kompliziert sich dann.

ImIm

ReRe

Bild 2.52: Verschiebung der Ortskurve G(jω)um

2.3. Hyperstabilit

at 89

G(s)

F {˜y, t}

ˆy

˜y

(a)

ˆy

˜y

F {ˆy, t}

F {˜y, t}

(b)

Bild 2.53: (a) Regelkreis mit k

unstlichem Durchgriﬀ

d. (b) Nichtlinearit

F {ˆy, t} =

F {ˆy + v

d, t}.

2.3.3 Hyperstabilit

at nichtlinearer MIMO-Systeme

Auch f

ur MIMO-Systeme gibt es ein Stabilit

atskriterium im Frequenzbereich

[138, 154]. Es ist aber nicht ganz einfach anzuwenden. Deshalb betrachten

wir im Weiteren ein leichter handhabbares Kriterium auf Basis der Zustands-

raumdarstellung.

Es l

asst sich zeigen, dass steuer- und beobachtbare, zeitinvariante MIMO-

Systeme

˙x = Ax + Bu,

y = Cx + Du

mit der R

uckf

uhrung

u = −F {y,t},

dargestellt in Bild 2.54, genau dann asymptotisch hyperstabil sind, wenn fol-

gender Satz erf

ullt ist.

Satz 8 (Hyperstabilit

at von MIMO-Regelkreisen). Gegeben sei ein

nichtlinearer Regelkreis mit der steuer- und beobachtbaren Regelstrecke

˙x = Ax + Bu,

y = Cx + Du

und der R

uckf

uhrung

u = −v = −F {y,t} .

Erf

ullt

90 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

˙x = Ax+ Bu

y = Cx+ Du

v = F {y,t}

Bild 2.54: Nichtlinearer MIMO-Regelkreis.

(1) die Regelstrecke die Kalman-Jakubovich-Gleichungen

R + RA = −LL

LV = C

− RB,

+ D = V

mit positiv deﬁnitem R, beliebig regul

arem L und beliebigem V und

(2) die R

uckf

uhrungsnichtlinearit

at F die Popov’sche Integralgleichung



(τ)y(τ) dτ ≥−ε

ur alle t ≥ 0,

dann und nur dann ist der Regelkreis asymptotisch hyperstabil.

Die Popov’sche Integralungleichung

uberpr

uft man im MIMO-Fall

ahnlich

wie im SISO-Fall. Aber wie l

ost man die Kalman-Jakubovich-Gleichungen?

Wir betrachten im Folgenden verschiedene L

osungsans

atze.

ur ein System ohne Durchgriﬀ, d. h. D = 0, vereinfachen sich die Kalman-

Jakubovich-Gleichungen zu

R + RA = −LL

= RB.

Bei Systemen mit Durchgriﬀ D = 0 ist die Situation komplizierter. Oft

kann man dann in den folgenden drei Schritten vorgehen:

Schritt 1: Man w

ahlt eine beliebige regul

are Matrix L,z.B.

L = I

und bestimmt aus dem linearen Gleichungssystem

R + RA = −LL

2.3. Hyperstabilit

at 91

die positiv deﬁnite Matrix R.

Schritt 2: Da L regul

ar ist, bestimmt man aus

LV = C

− RB

die Matrix

V = L

−1

− RB).

Schritt 3: Und schließlich setzt man D = D

voraus und erh

alt aus

D + D

= V

die Matrix

D =

V . (2.12)

Es f

allt nun sofort auf, dass die Matrix (2.12) im Allgemeinen nicht mit der

Durchgangsmatrix D der Systembeschreibung

ubereinstimmt. Man verwendet

daher folgenden Trick. Man bildet die k

unstliche Durchgriﬀmatrix

D =

V −D.

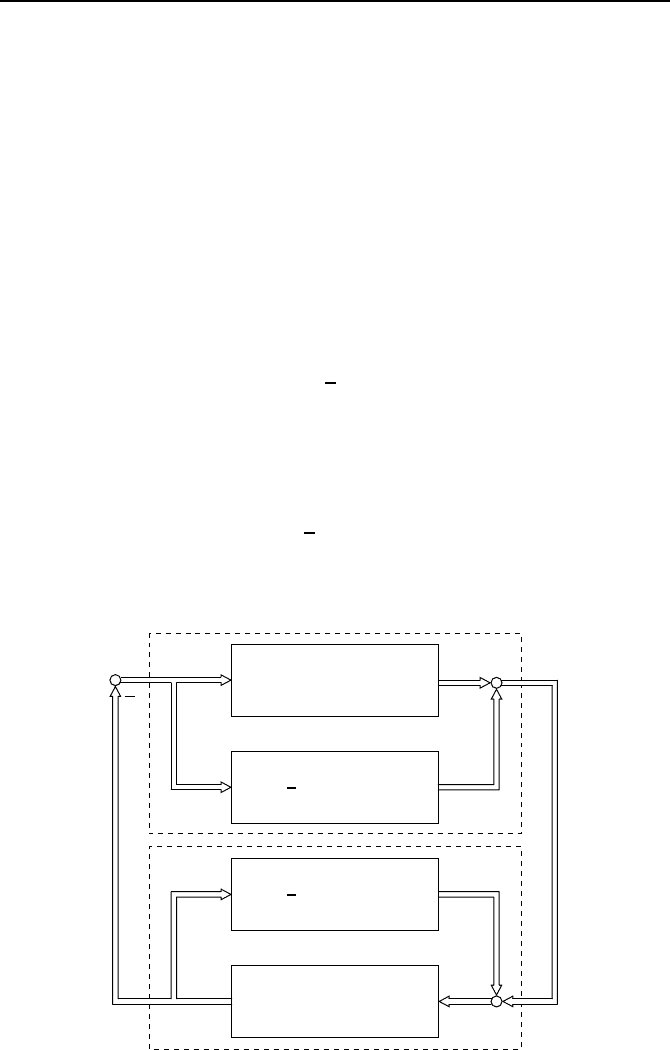
Dann formt man den Regelkreis aus Bild 2.54, wie in Bild 2.55 dargestellt, um.

ˆy

˙x = Ax + Bu

y = Cx + Du

V − D

F {y,t}

Bild 2.55: Regelkreis mit zus

atzlichem k

unstlichen Durchgriﬀ.

92 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Ersichtlich heben sich die zus

atzlichen Zweige mit

V −D gegenseitig auf.

Die Regelstrecke hat dann, wie in Gl. (2.12) gefordert, die Durchgangsmatrix

V .

Bez

uglich der Popov’schen Integralungleichung ist jetzt die Nichtlinearit

v = F {ˆy +

Dv,t}

zu betrachten. Auch hier tritt,

ahnlich wie im SISO-Fall, eine implizite Glei-

chung f

ur v auf. Dies kann bei der Auswertung der Popov’schen Integralun-

gleichung zu Schwierigkeiten f

uhren.

Manchmal k

onnen die Kalman-Jakubovich-Gleichungen auch auf andere

Weise als durch obige drei Schritte gel

ost werden. So kann auch zuerst die

Matrix V mittels einer Cholesky-Zerlegung aus

V = D

+ D

ermittelt werden. Die verbleibenden zwei Kalman-Jakubovich-Gleichungen

R + RA = −LL

und LV = C

− RB

bilden dann ein nichtlineares Gleichungssystem in R und L.Diesesl

ost man

und

uberpr

uft, ob eine L

osung mit positiv deﬁnitem R und regul

arem L

existiert.

2.3.4 Illustrationsbeispiele

Wir betrachten als ein einfaches Beispiel [86] das System

˙x =



−10

0 −3



x +





y =





x +





(2.13)

Von den Kalman-Jakubovich-Gleichungen l

osen wir zuerst die Gleichung

V = D + D

. Es gilt in diesem Fall mit D = I die Gleichung

V =

√

2I.

Aus den beiden verbleibenden Kalman-Jakubovich-Gleichungen

R + RA = −LL

und RB = C

− LV

folgt hier, wenn wir der Einfachheit halber R und L als Diagonalmatrizen

ansetzen,

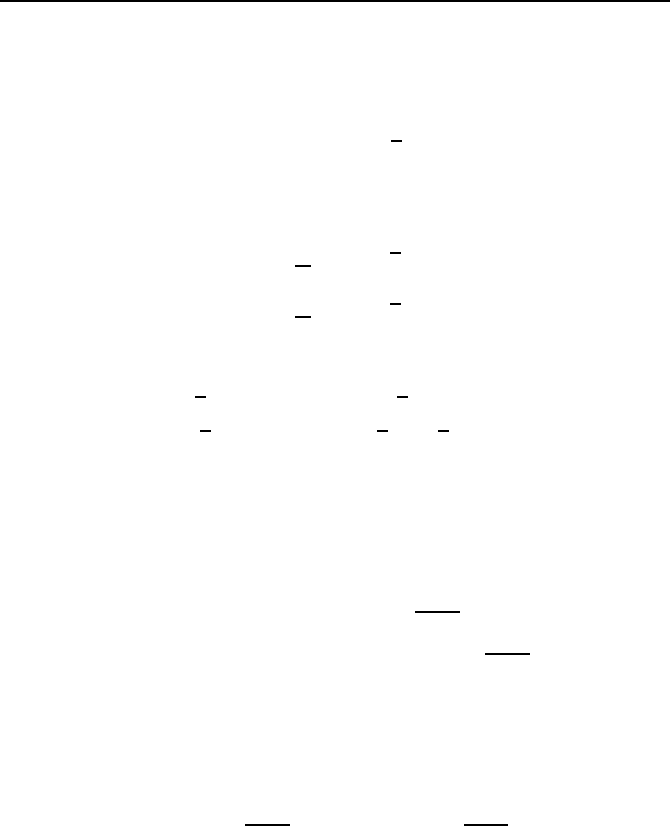
2.3. Hyperstabilit

at 93

−2



03r



= −



0 l



(2.14)

und



0 r







−

√



0 l



. (2.15)

Die Gleichungen (2.14) und (2.15) bilden das nichtlineare Gleichungssystem

=1−

√

=1−

√

Es besitzt die L

osungen

=3∓ 2

√

2 > 0,r

=7∓ 4

√

3 > 0,

= ±2 −

√

2 =0,l

= ±2

√

6 − 3

√

2 =0,

so dass die Matrix R positiv deﬁnit und die Matrix L regul

ar ist. Die Kalman-

Jakubovich-Gleichungen sind also erf

ullt.

Aus der Zustandsraumdarstellung (2.13) und auch aus der zugeh

origen

Ubertragungsmatrix

G(s)=C(sI − A)

−1

B + D =

⎡

⎢

⎣

s +2

s +1

s +4

s +3

⎤

⎥

⎦

ist ersichtlich, dass die beiden Diﬀerenzialgleichungen bzw. Teilsysteme nicht

verkoppelt sind. Wir k

onnen in diesem Fall auch beide Teilsysteme mittels

Satz 7 getrennt voneinander daraufhin untersuchen, ob sie positiv reell sind.

Da die Ortskurven von

(s)=

s +2

s +1

und G

(s)=

s +4

s +3

in Bild 2.56 rechts der imagin

aren Achse liegen und beide Teilsysteme stabil

sind, ist das Gesamtsystem, wie erwartet, streng positiv reell.

Als Regler verwenden wir zwei P-Regler, die einer Stellgr

oßenbeschr

ankung

unterliegen. Das Regelgesetz hat dann die Form

u = −v =



−sat(K

)

−sat(K

)



mit sat(x)=

⎧

⎪

⎨

⎪

⎩

−x

max

,x<−x

max

x, |x|≤x

max

,x>x

max

(2.16)

wobei K

> 0 und K

> 0 die Parameter der P-Regler sind.