J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

Nichtlineare Regelungen f

ur lineare

Regelstrecken

3.1 Regler mit Antiwindup

3.1.1 Der Windup-Eﬀekt

Jedes reale Stellglied eines Regelkreises besitzt eine Beschr

ankung der Stell-

oße u, da seine maximale Stellleistung endlich ist. Bild 3.1 illustriert einen

entsprechenden Regelkreis mit Regelstrecke G(s), Regler K(s) und Begren-

zungsglied, wobei die beiden Letzten das Stellglied enthalten. Die Begrenzung

der Stellgr

oße beschreibt man durch eine S

attigungskennlinie

u =sat(u

⎧

⎪

⎨

⎪

⎩

max

min

≤ u

max

min

Beispiele f

ur solche Begrenzungen der Stellgr

oße sind das maximale Dreh-

moment eines Stellmotors, der maximale Ruderwinkel eines Schiﬀes und der

maximale

Oﬀnungsgrad eines Ventils. Dabei hat die S

attigungskennlinie oft

symmetrische Grenzen, d. h., es gilt oft

min

= −u

max

min

max

K(s)

G(s)

Bild 3.1: Regelkreis mit linearer Regelstrecke, linearem Regler K(s) und einer Be-

grenzung der Stellgr

oße.

116 Kapitel 3. Regelungen f

ur lineare Regelstrecken

Uberschreitet die Stellgr

oße die Beschr

ankungen, so ist der Regelkreis nicht

mehr linear, was im Allgemeinen nachteilig f

ur seine Stabilit

at und sein Re-

gelverhalten ist. Wir wollen dies im Weiteren untersuchen.

Zu diesem Zweck betrachten wir die allgemeine Struktur eines PID-

Reglers, d. h.

K(s)=K



+ T



= K

(s)+

mit K

= K

. Der Regleranteil K

(s) kann je nach Typ des Gesamtreg-

lers ein P-, PD- oder D-Regler sein oder im Falle eines reinen I-Reglers auch

entfallen. F

ur den Fall u = u

,d.h.denunges

attigten Fall, ist der Regelkreis

oﬀensichtlich linear. Im ges

attigten Fall dagegen gilt

u = u

max

oder u = u

min

d. h., auf die Regelstrecke G(s) wirkt eine konstante Stellgr

oße u.

Eine Regelung kann im Fall der S

attigung aufgrund der konstanten Stell-

oße u nicht stattﬁnden. Der Regelkreis ist dann praktisch unterbrochen. Bild

3.2 illustriert dies. Oﬀensichtlich f

uhrt die Unterbrechung dazu, dass der In-

tegrierer die Regelabweichung solange auﬁntegriert, bis die Regelabweichung

ihr Vorzeichen wechselt. Diesen Vorgang nennt man Windup

[1]

. Die Auﬁnte-

gration ist nicht nur unn

utz, da ein Wert von

min

bzw. u

max

nicht auf die Regelstrecke wirken kann, sondern auch sch

adlich, da der hohe

Integralanteil nach einem Vorzeichenwechsel der Regelabweichung e wieder

abgebaut werden muss, bis u

innerhalb der S

attigungsgrenzen liegt. Erst

dann ist der Regelkreis wieder geschlossen und eine Regelung m

oglich. Auch

nach dem Vorzeichenwechsel von e bleibt der Regelkreis also noch eine Zeit

u = u

max

≥ u

max

min

G(s)

(s)

Unterbrechung

Bild 3.2: Regelkreis im S

attigungsfall.

[1]

engl.: wind up = aufwickeln, aufspulen, hochkurbeln.

3.1. Regler mit Antiwindup 117

lang unterbrochen. Dies ist f

ur das Regelverhalten ung

unstig und kann zu

erh

ohtem

Uberschwingen oder sogar zur Instabilit

at f

uhren.

Die Situation l

asst sich auch wie folgt interpretieren: Ist die Stellgr

oße in

attigung, der Regelkreis also unterbrochen, so bildet der Integralanteil des

Reglers ein instabiles Element im oﬀenen Kreis. Diese Situation ist nat

urlich

nicht erw

unscht.

3.1.2 PID-Regler mit Antiwindup

Die Vermeidung des oben beschriebenen Windups ist mittels einer Antiwind-

up-Struktur m

oglich. Diese verhindert, dass die Ausgangsgr

oße u

des Reglers

die Grenzen u

min

und u

max

uberschreitet. Bild 3.3 zeigt einen PID-Regler mit

Antiwindup. Die Kennlinie des Antiwindup-Elements ist eine Totzone

v =

⎧

⎪

⎨

⎪

⎩

m(u

− u

max

),u

max

0,u

min

≤ u

max

m(u

− u

min

),u

min

Dabei gilt f

ur die Steigung der Totzone m  0. Die Totzone realisiert eine

negative R

uckkopplung des Reglerausganges auf den Eingang des I-Anteils.

Liegt der Ausgangswert u

des Reglers innerhalb der Stellgr

oßenbeschr

ankung

min

und u

max

,soistdieR

uckkopplung nicht aktiv. D. h., der Regler arbeitet

als normaler PID-Regler.

Uberschreitet u

eine der Begrenzungen u

min

oder

max

, so wirkt die Totzone als starke Gegenkopplung auf den I-Anteil. Da-

bei f

uhrt die Gegenkopplung den I-Anteil sofort auf einen so niedrigen Wert

zur

uck, dass u

die Stellgr

oßenbeschr

ankung nicht verletzt. Da die Steigung

m endlich ist, k

onnen die Grenzen u

min

und u

max

durch die Stellgr

oße u

geringf

ugig

uberschritten werden. In der Praxis spielt das aber keine Rolle.

max

min

(s)

Antiwindup-Element

Bild 3.3: PID-Regler mit Antiwindup.

118 Kapitel 3. Regelungen f

ur lineare Regelstrecken

max

min

(s)

Antiwindup-Element

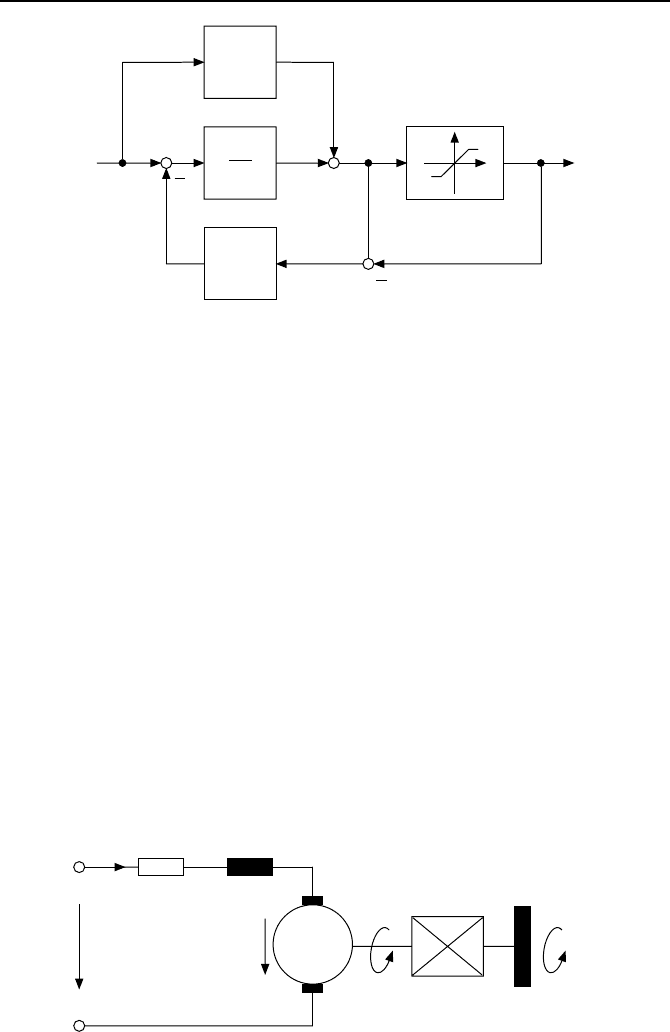
Bild 3.4: Alternative Struktur des Antiwindups aus Bild 3.3.

Eine Realisierung, die

aquivalent zur Antiwindup-Struktur des Bildes 3.3

ist, aber ohne Totzone auskommt, ist in Bild 3.4 dargestellt. Diese Realisie-

rung des Antiwindups hat den Vorteil, dass nur eine nichtlineare Kennlinie

erforderlich ist.

Neben obiger klassischer Antiwindup-Methode f

ur PID-Regler existiert ei-

ne Reihe weiterer Verfahren und dazugeh

origer Erweiterungen. Ein

Uberblick

hierzu ﬁndet sich in [198].

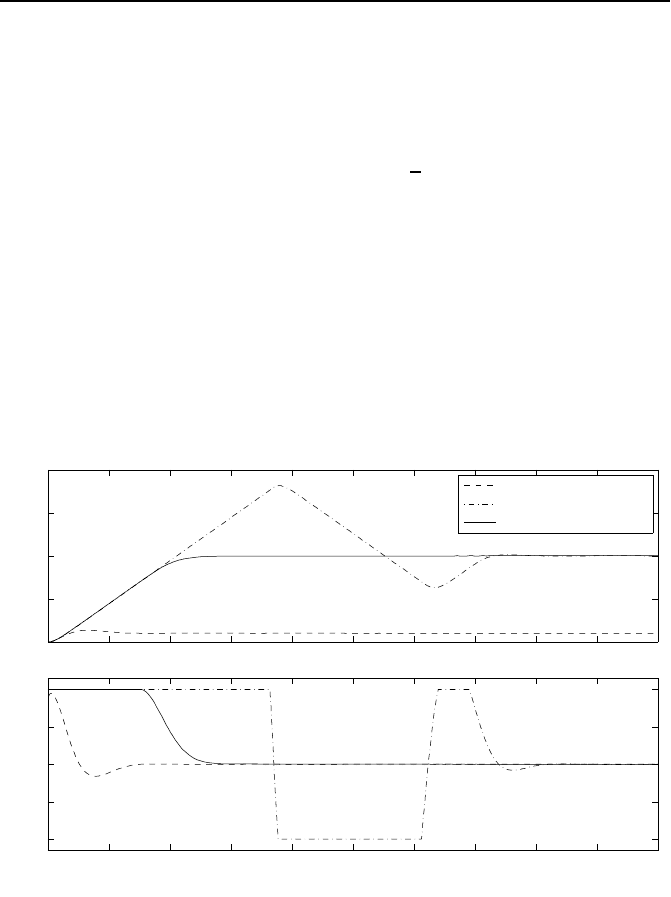
3.1.3 Beispiel Gleichstrommotor

Wir betrachten als Beispiel den Gleichstrommotor aus Bild 3.5, der als Servo-

antrieb arbeitet und zum Einstellen eines vorgebbaren Drehwinkels ϕ

dient.

In solchen Servoantrieben werden oft Antiwindup-Systeme in der Regelung

verwendet.

ur die Ankerspannung u gilt mit der im Motor induzierten Spannung k

und dem Ankerstrom i die Gleichung

ω,ϕ

Last

Getriebe

¨u

Bild 3.5: Gleichstrommotor mit Getriebe und Last.

3.1. Regler mit Antiwindup 119

u = Ri + L

i + k

ω. (3.1)

Dabei ist R der Widerstand, L die Induktivit

at, ϕ der Drehwinkel und ω =˙ϕ

die Winkelgeschwindigkeit des Ankers. Das erzeugte Drehmoment ist

M = k

und dieses ist gleich

M = J ˙ω + k

mit dem geschwindigkeitsproportionalen Reibungsterm k

ω. Hieraus folgt

i = J ˙ω + k

ω. (3.2)

Dabei gilt mit dem Tr

agheitsmoment J

des Ankers und dem Tr

agheitsmo-

ment J

der Last, das

uber das Getriebe mit der

Ubersetzung ¨u auf die An-

kerwelle r

uckgerechnet wird, f

ur das Gesamttr

agheitsmoment

J = J

¨u

Die Werte k

und k

sind Motorparameter.

Aus den Gl. (3.1) und (3.2) erh

alt man mit den Laplace-Transformierten

U(s), I(s), Φ(s)vonu, i, ϕ

U(s)=RI(s)+LI(s) · s + k

Φ(s) · s,

I(s)=

Φ(s) · s

Φ(s) · s,

wenn alle Anfangswerte identisch null sind. Setzt man obige Gleichungen in-

einander ein, so ergibt sich die

Ubertragungsfunktion

Φ(s)

U(s)







s +



+ k



Ber

ucksichtigt man noch ϕ =¨uϕ

, so gilt

G(s)=

(s)

U(s)

¨uLJ







s +





Mit den Motor- und Lastdaten R =8.9Ω,L=0.1H,J=0.1Nms

rad

−1

¨u =10,k

=1.7775 V s rad

−1

=4NmA

−1

und k

=0.1Nmsrad

−1

ergibt sich

G(s)=

s(s

+90s + 800)

120 Kapitel 3. Regelungen f

ur lineare Regelstrecken

Die Motorspannung u, d. h. die Stellgr

oße, unterliegt den Begrenzungen

−100 ≤ u ≤ 100.

Als Regler verwenden wir einen PI-Regler mit

H(s)=K

+ K

und den Parametern K

= 90 und K

= 150.

Die Simulationen in Bild 3.6 zeigen eine kleine Sprungantwort von ϕ

0 rad auf ϕ

=1rad=57.3

◦

mit linearer Ausregelung und eine große von

=0radaufϕ

= 10 rad = 573.0

◦

mit nichtlinearer Ausregelung. F

ur den

letztgenannten Fall eines PI-Reglers ohne Antiwindup, bei dem die Stellgr

oße

in die S

attigung geht, sind die negativen Auswirkungen des Windups des I-

Reglers klar ersichtlich. Deutlich erkennbar ist auch die positive Wirkung des

Antiwindups, das die durch das unn

otige Hochlaufen des Integrierers verur-

sachten Schwingungen beseitigt.

Zeit t in s

in rad

u in V

linear

ohne Antiwindup

mit Antiwindup

100

-50

-100

Bild 3.6: Winkelverlauf ϕ

und Motorspannung u f

ur den linearen Fall, den Fall mit

Antiwindup und den Fall ohne Antiwindup, bei dem der Regler in S

attigung ist.

3.1.4 Antiwindup f

ur allgemeine Reglerstrukturen

Es stellt sich die Frage, was im Fall eines allgemeineren Reglers

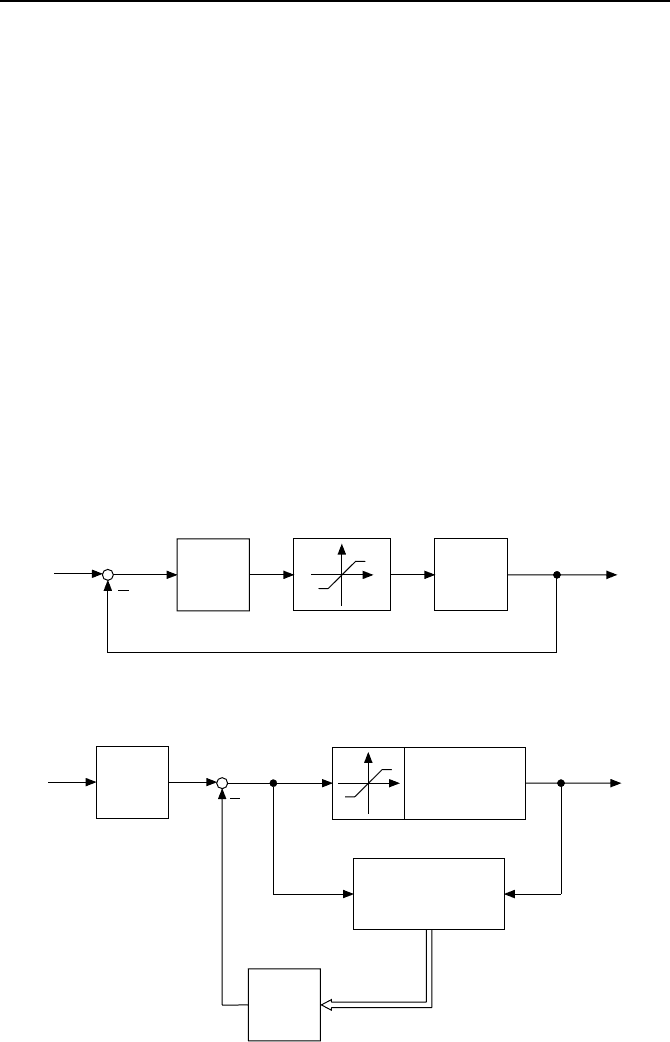
3.1. Regler mit Antiwindup 121

(s)=H(s) · E(s)

als dem PID-Regler an Antiwindup-Maßnahmen vorzusehen ist. Besitzt eine

Regler

ubertragungsfunktion H(s) instabile Pole oder Pole mit einem Realteil

gleich null, so tritt im Falle der Stellgr

oßenbegrenzung ebenfalls ein Weglaufen,

d. h. Windup, der Reglerzust

ande und damit der Reglerausgangsgr

oße u

auf.

Bild 3.7 zeigt die Struktur dieses allgemeineren Regelkreises. Auch f

ur diese

Regelkreise gibt es verschiedene Antiwindup-Methoden [41, 89, 99, 187].

Eine besonders plausible Antiwindup-Struktur f

ur den allgemeinen Fall

erh

alt man, wenn man einen kleinen Umweg macht, den wir auf den n

achsten

Seiten verfolgen wollen. Er besteht darin, Zustandsregler mit Beobachtern zu

betrachten und f

ur diese das Problem des S

attigungsfalles zu l

osen [71].

Wir betrachten den in Bild 3.8 dargestellten Zustandsregelkreis mit Be-

obachter, der auch Kontrollbeobachter genannt wird. Dabei ist die Stell-

oßenbeschr

ankung Teil der Regelstrecke und das Vorﬁlter V dient der Kom-

pensation der bleibenden Regelabweichung.

Der gesch

atzte Zustandsvektor ˜x entspricht nach einer gewissen Ein-

schwingzeit dem Zustandsvektor x der Regelstrecke, wenn u

min

≤ u

max

gilt, d. h., wenn der lineare Fall vorliegt. Man beachte, dass bei Nichterf

ullung

dieser Bedingung f

ur u

der Regelkreis, wie oben beschrieben, nichtlinear ist.

max

min

H(s)

G(s)

Bild 3.7: Regelkreis mit S

attigungskennlinie und beliebigem linearen Regler H(s).

˜x

˜x = A˜x + bu

+ l

y − c

˜x

˙x = Ax + bu

y = c

Regelstrecke

Beobachter

Bild 3.8: Zustandsregelkreis mit Kontrollbeobachter.

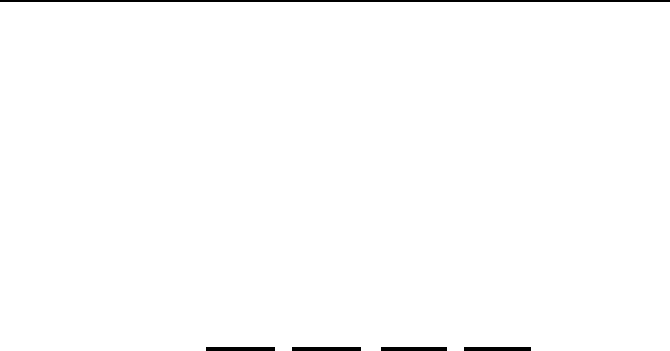
122 Kapitel 3. Regelungen f

ur lineare Regelstrecken

Dabei besitzt obiger Zustandsregelkreis mit Beobachter im linearen Fall

2n Eigenwerte. Dies sind – wie aus der Theorie linearer Beobachter und dem

Separationstheorem bekannt [124] – sowohl die n Eigenwerte der mit u =

−k

x geregelten Strecke, d. h. die Eigenwerte der Matrix

A = A − bk

als auch die n Eigenwerte der Beobachtermatrix

F = A − lc

Das charakteristische Polynom des Kontrollbeobachters ist also durch

P (s)=det



sI − A + bk





 

D(s)

det



sI − A + lc





 

Δ(s)

gegeben, d. h., es setzt sich aus dem charakteristischen Polynom D(s)des

Regelkreises und dem charakteristischen Polynom Δ(s) des Beobachters zu-

sammen. Dabei sind die Eigenwerte des Regelkreises und die des Beobachters

aufgrund des Separationstheorems durch den Reglervektor k und den Beob-

achtervektor l unabh

angig voneinander vorgebbar.

Verletzt die Stellgr

oße die Beschr

ankung, so sind u

und u verschieden. In

diesem Fall sind auch die Eingangsgr

oßen von Regelstrecke und Beobachter

verschieden, wie aus Bild 3.8 erkennbar ist. Beobachtungsfehler sind die Fol-

ge und die Ausregelqualit

at wird schlecht. Dieses Problem l

asst sich einfach

osen, indem man die Eingangsgr

oße u

des Beobachters ebenfalls durch die

Stellgr

oßenbegrenzung einschr

ankt. Dann haben Regelstrecke und Beobachter

immer dieselbe Stellgr

oße. Bild 3.9 zeigt die modiﬁzierte Struktur.

Durch das zus

atzliche S

attigungsglied sind Beobachtungsfehler ausge-

schlossen, die aus einer Verletzung der Stellgr

oßenbeschr

ankung resultieren.

Obige einfache Struktur erm

oglicht im Allgemeinen auch dann eine gute Aus-

regelqualit

at, wenn der Regelkreis vor

ubergehend in der S

attigung betrieben

wird. Dies gilt vor allem f

ur stabile Regelstrecken.

Wir betrachten nun den Beobachter

˜x =



A − lc



˜x + bu + ly = F ˜x + bu + ly

und erhalten mit den Laplace-Transformierten

X(s), U(s) und Y (s)

X(s) − ˜x(0) = F ·

X(s)+b · U(s)+l · Y (s)

und mit ˜x(0) = 0 die Gleichung

X(s)=(sI −F )

−1

b · U(s)+(sI − F )

−1

l · Y (s).

Zusammen mit dem Zustandsregler

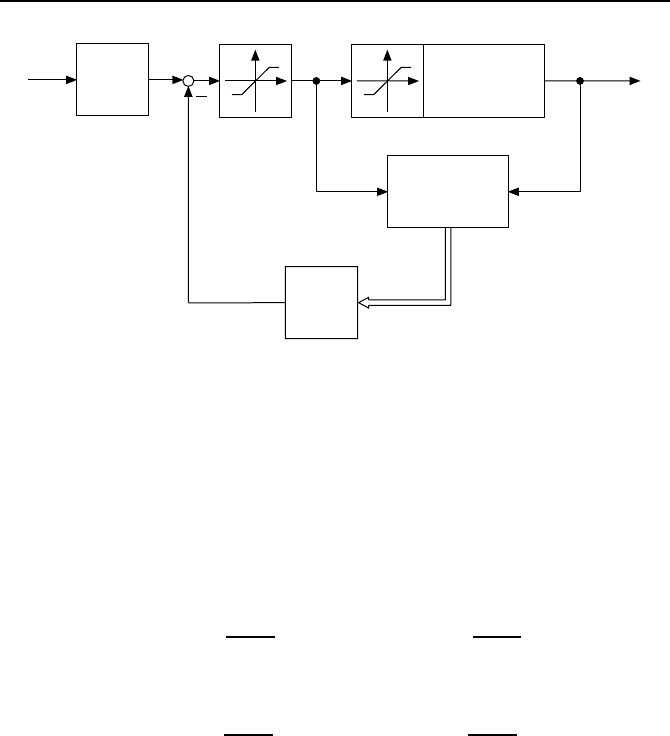
3.1. Regler mit Antiwindup 123

˜x

˜x = A ˜x + bu

+ l

y − c

˜x

˙x = Ax + bu

y = c

Regelstrecke

Beobachter

Bild 3.9: Regelkreis mit zus

atzlicher Begrenzungskennlinie zur Vermeidung negativer

Auswirkungen der Stellgr

oßenbegrenzung.

(s)=k

X(s)

gilt

(s)=k

(sI − F )

−1

b · U(s)+k

(sI − F )

−1

l · Y (s).

Man erh

alt also zwei

Ubertragungsfunktionen,

(s)=

(s)

U(s)

= k

(sI − F )

−1

b =

(s)

Δ(s)

und

(s)=

(s)

Y (s)

= k

(sI − F )

−1

l =

(s)

Δ(s)

die den Zusammenhang zwischen u

und u bzw. y beschreiben. H

(s) und

(s) haben denselben Nenner

Δ(s)=det(sI − F ).

Wir k

onnen den Regelkreis mit Beobachter also auch mittels

Ubertragungs-

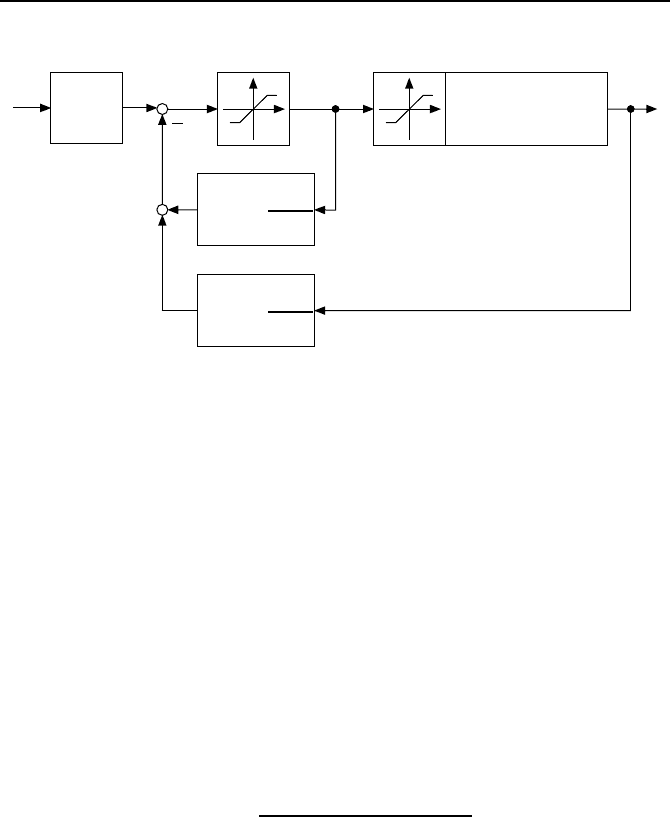
funktionen darstellen, so wie es Bild 3.10 zeigt. Bei dieser Betrachtungsweise

interpretieren wir jetzt die zus

atzliche S

attigungskennlinie

u =sat(u

)

als eine Art von Antiwindup-Element f

ur die

Ubertragungsglieder H

(s) und

(s). Denn das Antiwindup-Element vermeidet auch hier unerw

unschte Aus-

wirkungen der Stellgr

oßenbegrenzung bei den als Regler wirkenden

Ubertra-

gungsgliedern H

(s) und H

(s).

124 Kapitel 3. Regelungen f

ur lineare Regelstrecken

V (s)

G(s)= c

(sI−A)

−1

(s)=

(s)

Δ(s)

(s)=

(s)

Δ(s)

Regelstrecke

Antiwindup-

Element

Bild 3.10: Zustandsregelkreis mit Kontrollbeobachter, dargestellt durch

Ubertra-

gungsfunktionen, und Antiwindup-Element.

Es sei angemerkt, dass H

(s) und H

(s) die Nennerordnung n, also die

Systemordnung von A, besitzen, da wir den Zustandsvektor x vollst

andig re-

konstruiert haben. Im Falle eines reduzierten Beobachters weisen H

(s) und

(s) eine niedrigere Systemordnung auf, n

amlich die des reduzierten Beob-

achters.

Wir haben des Weiteren die Struktur des Regelkreises in Bild 3.10 ver-

allgemeinert, indem wir anstelle des Vorﬁlters V eine

Ubertragungsfunktion

V (s) als Vorﬁlter zulassen. Die Funktionsweisen des Antiwindups sowie des

Zustandsreglers mit Beobachter bleiben davon unbeeinﬂusst.

Wir betrachten nun wieder den klassischen Regelkreis mit einer Regelstre-

cke G(s) und einem Regler H(s)f

ur den wir ein Antiwindup suchen. Dieser

Regelkreis, der in den Bildern 3.7 und 3.11 dargestellt ist, hat im linearen,

d. h. unges

attigten Fall die

Ubertragungsfunktion

G(s)=

(s)Z(s)

(s)N(s)+Z

(s)Z(s)

Die Regelkreisstruktur aus Bild 3.11 l

asst sich in die

aquivalente Struktur des

Bildes 3.12 umformen. Dabei f

uhrt man zus

atzlich das Polynom Δ(s)ein.

Denn dann entspricht die Struktur aus Bild 3.12 bis auf das Antiwindup-

Element vollst

andig der des Zustandsregelkreises mit Beobachter aus Bild

3.10. Das Antiwindup-Element f

ugt man nun auch in den Regelkreis aus Bild

3.12 ein. Bild 3.13 zeigt den sich so ergebenden Regelkreis mit Antiwindup.

Man hat auf diese Weise aus den

Uberlegungen zur Vermeidung von

attigungseﬀekten beim Zustandsregler mit Beobachter ein Antiwindup f

den Standardregelkreis mit beliebigem linearen Regler H(s) gewonnen. Die

zuletzt betrachtete Regelkreisstruktur des Bildes 3.13 bildet also die L

osung