J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.

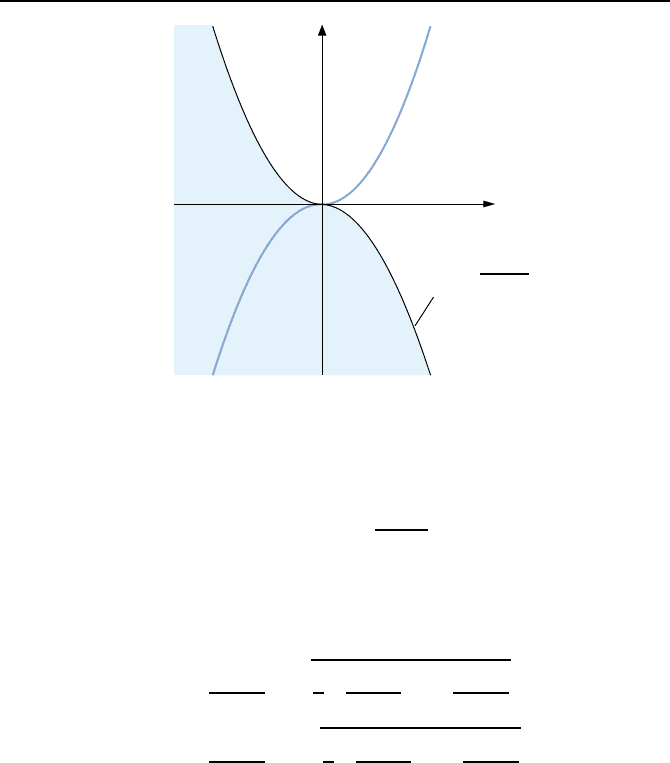
3.2. Zeitoptimale Regelung und Steuerung 135
x
10
x
20
S(x
2
)=−
x
2
|x
2
|
2u
max
−u
max
,
α = −1
u
max
,
α =1
Bild 3.18: Durch die Schaltkurve x
1
= S(x
2
)inzweiH
¨
alften geteilter Zustandsraum.
getrennt. Diese Parabel
¨
aste bilden zusammen die Schaltkurve
S(x
2
)=x
1
= −
x
2
|x
2
|
2u
max
. (3.20)
Unterhalb von S(x
2
) gilt u = u
max
,oberhalbu = −u
max
. Bild 3.18 zeigt den
Sachverhalt.
Mit dem obigen Ergebnis sind die Schaltzeitpunkte
t
1
= −
x
20
αu
max
±
)
1
2
x
20
αu
max
2
−
x
10
αu
max
,
t
2
= −
x
20
αu
max
± 2
)
1
2
x
20
αu
max
2
−
x
10
αu
max
mit
α =
1,x
1
<S(x
2
),
−1,x
1
>S(x
2
),
und α =
1,x
1
= S(x
2
) < 0,
−1,x
1
= S(x
2
) > 0,
bestimmt. Die zeitoptimale Steuerung liegt somit vor. Auch das zeitoptima-
le Regelungsgesetz l
¨
asst sich jetzt ermitteln. Oberhalb der Schaltlinie S(x
2
)
verwendet man −u
max
,unterhalbu
max
,d.h.
u(x)=
u
max
,x
1
− S(x
2
) < 0,
−u
max
,x
1
− S(x
2
) > 0.
Das l
¨
asst sich auch in der Form
136 Kapitel 3. Regelungen f
¨
ur lineare Regelstrecken
u =
u
max
, sgn(x
1
− S(x
2
)) < 0,
−u
max
, sgn(x
1
− S(x
2
)) > 0
= −u
max
· sgn(x
1
− S(x
2
)) = u
max
· sgn(S(x
2
) − x
1
)
darstellen. Das zeitoptimale Regelgesetz der Strecke 1/s
2
hat dann mit Gl.
(3.20) die Form
u = u
max
· sgn
−
x
2
|x
2
|
2u
max
− x
1
.
Auf der Schaltlinie, d. h. f
¨
ur x
1
= S(x
2
), ergibt obiges Regelgesetz den Wert
u = 0. Korrekterweise m
¨
usste dort u = ±u
max
sein. In der Praxis spielt das
jedoch keine Rolle. Die zugeh
¨
orige Regelung zeigt Bild 3.19.
u
S(x
2
)
u
max
−u
max
1
s
1
s
x
10
x
20
x
1
x
2
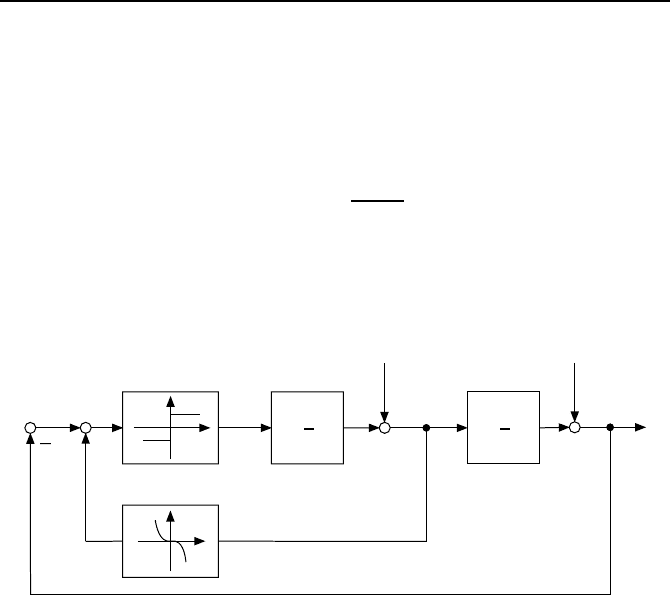
Bild 3.19: Zeitoptimale Regelung f
¨
ur 1/s
2
.
Obiges Regelgesetz und weitere zeitoptimale Regelgesetze f
¨
ur Regelstre-
cken zweiter Ordnung mit reellen Eigenwerten lassen sich auch relativ einfach
durch Analyse der Trajektorien f
¨
ur u = u
max
und u = −u
max
in der Zustands-
ebene herleiten. Teile dieser Trajektorien bilden offensichtlich die Menge aller
Trajektorien des zeitoptimal geregelten Systems. Insbesondere die Schaltli-
nie S ist identisch mit Teilen der zwei Trajektorien, die f
¨
ur u = u
max
bzw.
u = −u
max
durch den Ursprung x = 0 laufen. Es ist daher f
¨
ur die Herleitung
des zeitoptimalen Regelgesetzes ausreichend, diese beiden Trajektorien zu be-
rechnen und aufgrund von geometrischer
¨
Uberlegungen in der Zustandsebene
die Schaltlinie S aus Teilen dieser Trajektorien zusammenzusetzen.
3.2.4 Zeitoptimale Regler f
¨
ur Systeme niedriger Ordnung
Wir betrachten im Weiteren Systeme zweiter und dritter Ordnung und ihre
zeitoptimalen Regelgesetze. Als ersten Fall behandeln wir Regelstrecken
˙x =
01
0 −a
x +
0
1
u (3.21)
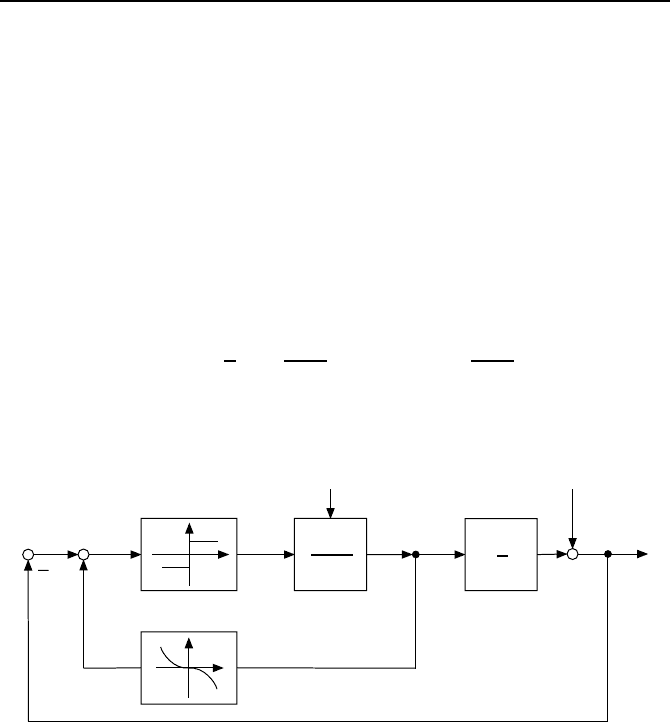
3.2. Zeitoptimale Regelung und Steuerung 137
mit einem Eigenwert bei null und einem Eigenwert λ = −a<0. Die Stell-
gr
¨
oßenbeschr
¨
ankung ist, wie auch bei allen weiteren Regelstrecken, durch
|u|≤u
max
gegeben. Man beachte, dass alle steuerbaren Regelstrecken mit obiger Ei-
genwertkonfiguration in die Form (3.21), die Regelungsnormalform, gebracht
werden k
¨
onnen.
Das zeitoptimale Regelgesetz lautet
u = u
max
sgn(S(x
2
) − x
1
)
mit der Schaltlinie
S(x
2
)=−
1
a
x
2
+
u
max
a
2
sgn(x
2
)ln
1+
a|x
2
|
u
max
.
Bild 3.20 zeigt das zugeh
¨
orige Strukturbild.
u
S(x
2
)
u
max
−u
max
1
s + a
1
s
x
10
x
20
x
1
x
2
Bild 3.20: Zeitoptimale Regelung f
¨
ur 1/s(s + a).
Als zweiten Fall betrachten wir stabile Regelstrecken zweiter Ordnung mit
reellen, von null verschiedenen Eigenwerten λ
1
<λ
2
< 0. Dabei gehen wir
davon aus, dass die Systembeschreibung in der Form
˙x =
λ
1
0
0 λ
2
x +
λ
1
λ
2
u (3.22)
vorliegt oder in diese transformiert wurde. Dann hat das zeitoptimale Regel-
gesetz die Form
u = u
max
sgn(S(x
2
) − x
1
)
mit

138 Kapitel 3. Regelungen f
¨
ur lineare Regelstrecken
S(x
2
)=u
max
sgn(x
2
)
+
1+
|x
2
|
u
max
λ
1
/λ
2
− 1
,
.
Auch f
¨
ur Systeme dritter Ordnung mit zwei Eigenwerten bei null und ei-
nem negativen Eigenwert λ = −a, die in Regelungsnormalform vorliegen oder
in diese transformiert wurden, kann das zeitoptimale Regelgesetz angegeben
werden [10]. Wir transformieren zu diesem Zweck die Regelungsnormalform
˙
˜x =
⎡
⎣
01 0
00 1
00−a
⎤
⎦
˜x +
⎡
⎣
0
0
1
⎤
⎦
u
mittels
˜x =
1
a
3
⎡
⎣
10 1
0 a −a
00 a
2
⎤
⎦
x
in die Form
˙x =
⎡
⎣
0 a 0
00 0
00−a
⎤
⎦
x +
⎡
⎣
−a
a
a
⎤
⎦
u. (3.23)
F
¨
ur die zeitoptimale Regelung des Systems (3.23) gilt
u = u
max
sgn(S(x
1
,x
2
) − x
3
) (3.24)
mit
S(x
1
,x
2
)=u
max
d
-
e
c
· (2 − e
√
b
) − 1
.
,
d =sgn
x
1
+ x
2
+
x
2
|x
2
|
2u
max
,
b =
x
2
2
2u
2
max
+
d
u
max
(x
1
+ x
2
),
c =
d · x
2
u
max
+
√
b.
Lag die Regelstrecke urspr
¨
unglich nicht in der jeweiligen Zustandsraum-
darstellung (3.21), (3.22) oder (3.23) vor, sondern wurde in diese Form ge-
bracht, so muss das entsprechende Regelgesetz durch R
¨
ucktransformation auf
die Ursprungskoordinaten der Regelstrecke umgerechnet werden.
F
¨
ur Regelstrecken h
¨
oherer Ordnung k
¨
onnen im Allgemeinen keine analy-
tisch angebbaren Regelgesetze mehr bestimmt werden. Im Fall stabiler Re-
gelstrecken mit ausschließlich verschiedenen reellen Eigenwerten erh
¨
alt man
dann ein Regelgesetz, bei dem ein nichtlineares Gleichungssystem f
¨
ur die Be-
stimmung von u zu l
¨
osen ist [10]. Im Fall von Regelstrecken mit konjugiert
komplexen Eigenwerten ist bis auf Ausnahmef
¨
alle, z. B. Regelstrecken zwei-
ter Ordnung [51, 121], eine Bestimmung und Realisierung unter praktischen
Gesichtspunkten nicht mehr m
¨
oglich.

3.2. Zeitoptimale Regelung und Steuerung 139
3.2.5 Beispiel U-Boot
U-Boote k
¨
onnen dynamisch und statisch tauchen. Beim dynamischen Tau-
chen wird w
¨
ahrend der Fahrt des Bootes das Tiefenruder so verstellt, dass
eine Abtriebskraft entsteht. Diese l
¨
asst das Boot in tiefere Wasserschichten
fahren, obwohl das Boot nicht schwerer ist als das von ihm verdr
¨
angte Wasser.
Beim statischen Tauchen wird dagegen Meerwasser in die daf
¨
ur vorgesehenen
Tanks aufgenommen. Folglich wird das Boot schwerer und sinkt. Soll das Boot
steigen, so wird das Wasser wieder aus den in Bild 3.21 dargestellten Tanks
mittels Pressluft herausgedr
¨
uckt. Wir wollen im Weiteren eine zeitoptimale
Tiefenregelung f
¨
ur das statische Tauchen entwerfen.
h
Ballasttank
Bild 3.21: U-Boot.
Nehmen wir an, dass das U-Boot so austariert ist, dass es in einer be-
stimmten Tiefe h schwebt und die Masse m aufweist. Die Tiefe h messen wir
beginnend von der Meeresoberfl
¨
ache aus mittels des Wasserdrucks. Wird dann
zus
¨
atzlich Wasser der Masse Δm in die Tanks verbracht oder ausgeblasen, so
entsteht die vertikal auf das Boot wirkende Kraft
F = Δm · g.
Dabei gilt Δm m. Die Ballastwassermasse l
¨
asst das U-Boot, das insgesamt
die Masse m + Δm aufweist, mit der Beschleunigung
¨
h =
g · Δm
m + Δm
≈
g
m
· Δm (3.25)

140 Kapitel 3. Regelungen f
¨
ur lineare Regelstrecken
steigen oder sinken. Ist Δm < 0 steigt es, ist Δm > 0sinktes.
Die vom U-Boot aufzunehmende bzw. auszublasende Ballastwassermasse
Δm
soll
wird einer Regelung, die der noch zu entwerfenden Tiefenregelung
unterlagert ist, als Sollwert vorgegeben. Diese Regelung l
¨
asst sich durch die
Differenzialgleichung
(Δm)
·
+ aΔm = aΔm
soll
(3.26)
beschreiben.
Setzt man Gl. (3.25) in Gl. (3.26) ein, so ergibt sich
...
h + a
¨
h =
a · g
m
· Δm
soll
.
Im Weiteren verwenden wir
˜u =
g
m
· Δm
soll
als Stellgr
¨
oße f
¨
ur die Tiefenregelung. Wir w
¨
ahlen als Zustandsvektor
˜x =
⎡
⎣
h
˙
h
¨
h
⎤
⎦
.
Des Weiteren w
¨
ahlen wir die Parameter a und m sowie die Einheiten der Va-
riablen so, dass wir das Modell des schwedischen U-Bootes der Firma Kocku-
mation AB,
˙
˜x =
⎡
⎣
01 0
00 1
00−0.005
⎤
⎦
˜x +
⎡
⎣
0
0
0.005
⎤
⎦
˜u,
mit der Tauchtiefe als Ausgangsgr
¨
oße
y =˜x
1
und ˜u
max
=0.005 aus [65] erhalten.
Um das zeitoptimale Regelgesetz (3.24) als Tauchtiefenregelung verwenden
zu k
¨
onnen, transformieren wir die Stellgr
¨
oße ˜u mittels
˜u = 200u
und erhalten so die Systembeschreibung
˙
˜x =
⎡
⎣
01 0
00 1
00−0.005
⎤
⎦
˜x +
⎡
⎣
0
0
1
⎤
⎦
u, (3.27)
y =˜x
1
3.2. Zeitoptimale Regelung und Steuerung 141
mit
|u|≤u
max
=2.5 · 10
−5
.
Wir k
¨
onnen nun das Regelgesetz (3.24) f
¨
ur die Regelstrecke (3.27) verwenden.
Dabei m
¨
ussen wir allerdings die in Gl. (3.24) auftretenden transformierten
Zustandsgr
¨
oßen
x = a
3
⎡
⎣
101
0 a −a
00a
2
⎤
⎦
−1
· ˜x =
⎡
⎣
a
3
0 −a
0 a
2
a
00a
⎤
⎦
˜x
verwenden, um u zu berechnen. Es gilt a =0.005. Obige Transformations-
gleichung eingesetzt in Gl. (3.24) ergibt f
¨
ur das zeitoptimale Regelgesetz des
U-Bootes in Originalkoordinaten
u = u
max
sgn(
˜
S(˜x
1
, ˜x
2
, ˜x
3
) − a˜x
3
)
mit
˜
S(˜x
1
, ˜x
2
, ˜x
3
)=u
max
d
-
e
c
· (2 − e
√
b
) − 1
.
,
d =sgn
a˜x
1
+˜x
2
+
(a˜x
2
+˜x
3
)|a˜x
2
+˜x
3
|
2u
max
,
b =
a
2
(a˜x
2
+˜x
3
)
2
2u
2
max
+
da
2
(a˜x
1
+˜x
2
)
u
max
,
c =
ad(a˜x
2
+˜x
3
)
u
max
+
√
b.
Wir betrachten als Beispiel das Auftauchen des U-Bootes aus 100 m Tiefe.
D. h., wir betrachten den Anfangsvektor
˜x(0) =
⎡
⎣
100
0
0
⎤
⎦
.
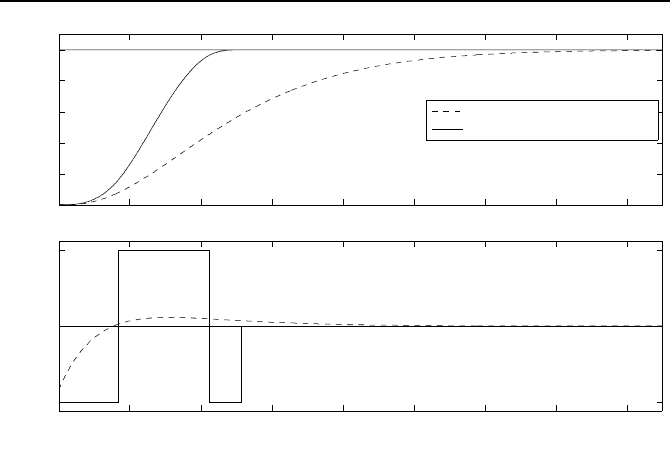
Bild 3.22 zeigt den Tiefenverlauf ˜x
1
(t) und den Stellgr
¨
oßenverlauf, den die
zeitoptimale Regelung produziert. Zum Vergleich sind die Verl
¨
aufe auch f
¨
ur
einen sehr guten linearen Regler,
˜u = 200u = −
4.164 ·10
−5
2.128 ·10
−2
2.592
˜x,
dargestellt, der so entworfen wurde, dass er nicht
¨
uberschwingt und gleichzei-
tig eine kurze Ausregelzeit aufweist. Klar ersichtlich ist die wesentlich schnelle-
re Ausregelgeschwindigkeit der zeitoptimalen Regelung. Diese wird allerdings
durch einen erh
¨
ohten Stellaufwand, d. h. Energieverbrauch, erkauft.
142 Kapitel 3. Regelungen f
¨
ur lineare Regelstrecken
100
80
60
40
20
0
0
-0.005
0.005
0
0
200
200
400
400
600
600
800
800
1000
1000
1200
1200
1400
1400
1600
1600
Stellgr
¨
oße ˜u
Tauchtiefe ˜x
1
in m
Zeit t in s
lineare Regelung
zeitoptimale Regelung
Bild 3.22: Tauchtiefenverl
¨
aufe ˜x
1
(t)=h(t) und Stellgr
¨
oßenverl
¨
aufe ˜u(t) der linearen
und zeitoptimalen Regelung des U-Bootes.
3.2.6 Zeitoptimale Vorsteuerung
In den betrachteten F
¨
allen von Regelstrecken zweiter und dritter Ordnung mit
reellen Eigenwerten ist die Bestimmung des zeitoptimalen Regelgesetzes u(x)
relativ einfach. Im Fall von Regelstrecken h
¨
oherer Ordnung kann im Allge-
meinen das zeitoptimale Regelgesetz nicht mehr analytisch bestimmt werden.
Entwurf und Realisierung sind dann, wie erw
¨
ahnt, nicht mehr oder nur mit
sehr hohem Aufwand m
¨
oglich. Zeitoptimale Steuerungen sind dagegen meis-
tens noch mit vertretbarem Aufwand bestimmbar und praktisch realisierbar.
Insbesondere ist ihre Verwendung sinnvoll bei Systemen, die sich repetierend
nur von einem Punkt x
1
zu einem Punkt x
2
bewegen. D. h. bei Systemen, die
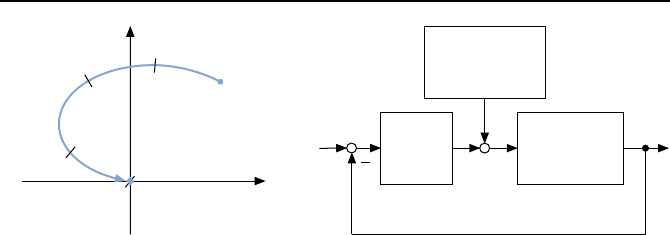
immer wieder erneut dieselbe Trajektorie abfahren, wie in Bild 3.23 gezeigt.
Um dann eventuelle St
¨
orungen oder kleine Abweichungen zu eliminieren, ver-
wendet man eine
¨
uberlagerte Regelung, wie in Bild 3.24 dargestellt.
In der Praxis zeigt sich, dass die existierenden Algorithmen zur Berechnung
der Schaltzeiten zeitoptimaler Steuerungen [23, 45] bei Strecken h
¨
oherer Ord-
nung mit komplexen Eigenwerten numerische Probleme aufweisen. In diesen
F
¨
allen kann ebenfalls oft keine zeitoptimale L
¨
osung sicher bestimmt werden.
Eine L
¨
osung dieser Problematik bietet die Berechnung der schrittoptimalen
Steuerfolge von zeitdiskreten Systemen. Hierbei wandelt man das zeitkonti-
nuierliche System in ein zeitdiskretes um. Die schrittoptimalen Steuerfolgen
zeitdiskreter linearer Systeme k
¨
onnen relativ problemlos mittels Verfahren der
3.3. Strukturvariable Regelungen ohne Gleitzustand 143
t
1
t
2
t
3
t
4
x
1
x
2
Bild 3.23: Zeitoptimale Trajektorie
mit den Schaltzeiten t
1
,t
2
,t
3
,t
4
.
y
soll
u
y
Regler
Regelstrecke
Zeitoptimale
Vorsteuerung
Bild 3.24: Regelkreis mit zeitoptimaler Vor-
steuerung.
linearen Programmierung berechnet werden [14, 30, 166, 183]. Je kleiner dabei
die Abtastzeit gew
¨
ahlt wurde, desto besser approximiert die schrittoptimale
Steuerfolge die zeitoptimale Steuerfunktion zeitkontinuierlicher Systeme.
Vergleicht man zeitoptimale Regelungen mit linearen, so erkennt man fol-
gendes Dilemma. Zeitoptimale Regelungen sind schnell in ihrem Ausregelver-
halten, aber sehr aufwendig zu entwerfen und zu realisieren. Lineare Rege-
lungen sind im Vergleich dazu langsam, aber sehr einfach zu berechnen und
zu implementieren. Gleiches gilt in abgemilderter Form auch f
¨
ur zeitoptimale
Steuerungen. Man kann offensichtlich nicht gleichzeitig ein sehr gutes Aus-
regelverhalten und die Einfachheit von Entwurf und Realisierung haben. Es
gibt allerdings einen zwischen beiden Extremen liegenden Kompromiss. Diesen
bilden die im n
¨
achsten Kapitel behandelten strukturvariablen Regelungen.
3.3 Strukturvariable Regelungen ohne Gleitzustand
3.3.1 Grundlagen strukturvariabler Regelungen
Bei strukturvariablen Regelungen k
¨
onnen verschiedene Typen unterschieden
werden. Eine wichtige Klasse sind parameter- und strukturumschaltende Rege-
lungen. Bei diesen wird zwischen verschiedenen Reglern in Abh
¨
angigkeit vom
Zustandsvektor x umgeschaltet. Als Regelstrecken werden lineare Systeme
˙x = Ax + bu
betrachtet, wobei die Stellgr
¨
oße u oft einer Beschr
¨
ankung
−u
max
≤ u ≤ u
max
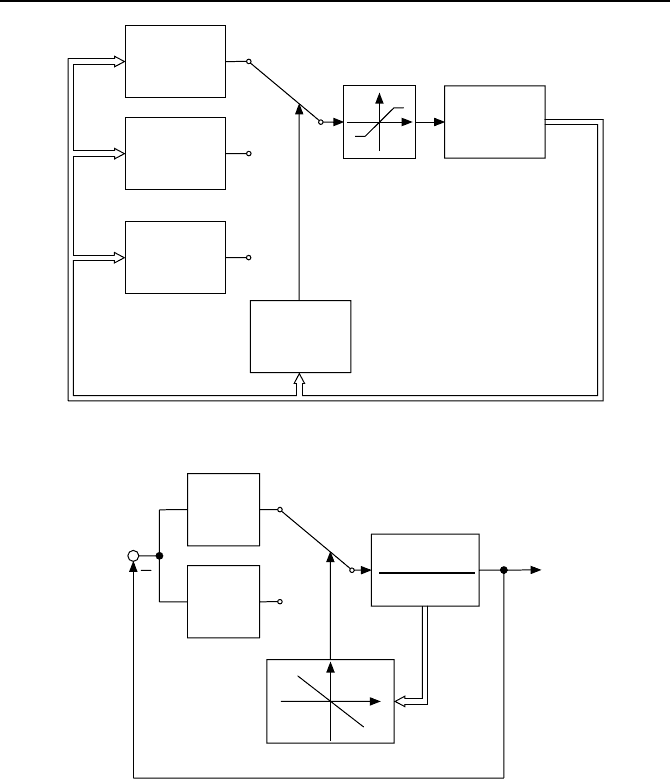
unterliegt. Bild 3.25 zeigt den prinzipiellen Aufbau eines solchen Regelkreises.
Bei umschaltenden Regelungen sind zwei m
¨
ogliche F
¨
alle von dynami-
schem Verhalten zu unterscheiden. Im Folgenden sollen sie an einem Beispiel
144 Kapitel 3. Regelungen f
¨
ur lineare Regelstrecken
x
Regler 1
Regler 2
Regler l
Auswahl-
strategie
.
.
.
˙
x =Ax+bu
Bild 3.25: Strukturvariables Regelungssystem.
e
u
y
x
x
1
x
2
k
1
k
1
k
2
k
2
1
s
2
+a
1
s+a
0
Umschaltstrategie
Bild 3.26: Regelkreis mit Umschaltung zwischen zwei P-Reglern mit k
1
und k
2
.
erl
¨
autert werden. Wir betrachten eine Umschaltung mit zwei P-Reglern und
einer Regelstrecke zweiter Ordnung, wie in Bild 3.26 dargestellt.
Die Umschaltstrategie arbeitet wie folgt. Eine Schaltgerade
s(x)=r
T
x =0
teilt den Zustandsraum. Rechts von ihr ist der Regler mit der Verst
¨
arkung k
1
aktiviert, links der mit k
2
. Das Regelgesetz hat die Form
u =
k
1
e, s(x) > 0,
k
2
e, s(x) < 0.
