J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.


166 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
des Systems k
¨
onnen im Allgemeinen als Funktion eines Parametervektors ρ
dargestellt werden als
u
R
= u
R
(ρ),
x
R
= x
R
(ρ),
d
R
= d
R
(ρ)
und
y
R
= g(x
R
(ρ)) = y
R
(ρ).
Die Dimension des Parametervektors ρ bezeichnen wir im Weiteren mit l.
Aus der Menge
E = {u
R
(ρ), x
R
(ρ), d
R
(ρ), y
R
(ρ), ρ ∈ M ⊂ IR
l
}⊂IR
m+n+s+r
von Ruhelagen wird eine Anzahl von p Ruhelagen (bzw. Arbeitspunkten)
(u
R
(ρ
i
), x
R
(ρ
i
), d
R
(ρ
i
), y
R
(ρ
i
)),i=1, ..., p,
ausgew
¨
ahlt. Um diese herum wird jeweils ein linearisiertes Modell
Δ ˙x
i
= A(ρ
i
)Δx
i
+ B(ρ
i
)Δu
i
+ S(ρ
i
)Δd
i
,
Δy
i
= C(ρ
i
)Δx
i
hergeleitet, wobei
Δx
i
= x − x
R
(ρ
i
),
Δu
i
= u − u
R
(ρ
i
),
Δd
i
= d − d
R
(ρ
i
),
Δy
i
= y − y
R
(ρ
i
)
und
A(ρ
i
)=
∂f(x, d
R
(ρ
i
), u
R
(ρ
i
))
∂x
x=x
R
(ρ
i
)
,
B(ρ
i
)=
∂f(x
R
(ρ
i
), d
R
(ρ
i
), u)
∂u
u=u
R
(ρ
i
)
,
S(ρ
i
)=
∂f(x
R
(ρ
i
), d, u
R
(ρ
i
))
∂d
d=d
R
(ρ
i
)
,
C(ρ
i
)=
∂g(x)
∂x
x=x
R
(ρ
i
)
gilt.
Im Weiteren wollen wir die Vektoren ρ
i
stellvertretend f
¨
ur
4.1. Gain-scheduling-Regler 167
x
u
1
2
3
4
5
6
G
¨
ultigkeitsbereich des
linearisierten Modells 5
Menge aller Ruhelagen (u
R
(ρ),x
R
(ρ))
(u
R
(ρ
3
),x
R
(ρ
3
))
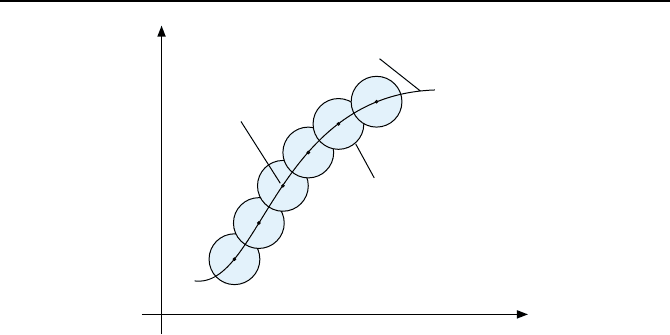
Bild 4.1: G
¨
ultigkeitsbereiche der parametrierten Linearisierungsfamilie.
(u
R
(ρ
i
), x
R
(ρ
i
), d
R
(ρ
i
), y
R
(ρ
i
))
als Arbeitspunkte bezeichnen. Die Menge der linearisierten Modelle bezeich-
net man als parametrierte Linearisierungsfamilie der Regelstrecke. Diese p li-
nearisierten Modelle haben immer nur einen beschr
¨
ankten G
¨
ultigkeitsbereich
um die jeweiligen Arbeitspunkte herum. Die G
¨
ultigkeitsbereiche sollten dabei
l
¨
uckenlos aneinander anschließen bzw. sich
¨
uberlappen, wie es Bild 4.1 illus-
triert. Die parametrierte Linearisierungsfamilie deckt mit ihren G
¨
ultigkeitsbe-
reichen oft nicht den gesamten Raum der Eingangs- und Zustandsgr
¨
oßen ab,
so dass außerhalb dieser Bereiche diese Modellfamilie das Verhalten des nicht-
linearen Systems nicht mehr widerspiegelt.
F
¨
ur jedes der p linearisierten Modelle mit dem Parametervektor ρ
i
wird
ein Regler
˙z
i
= h
i
(z
i
,Δd
i
,Δx
i
,Δy
i
,Δw
i
),
Δu
i
= k
i
(z
i
,Δx
i
,Δy
i
,Δw
i
)
bestimmt, dessen optionale Dynamik durch eine Differenzialgleichung mit den
Reglerzust
¨
anden z
i
festgelegt ist. Dabei ist
Δw
i
= w − w
R
(ρ
i
)
die Abweichung des Sollgr
¨
oßenvektors w vom Arbeitspunkt w
R
(ρ
i
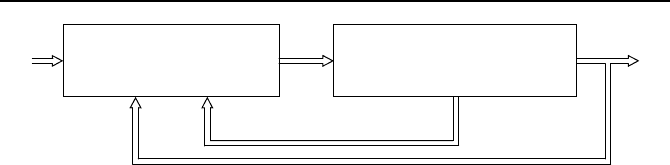
). Bild 4.2
zeigt den i-ten dieser p Regelkreise, der aus dem i-ten Teilregler und der im
Arbeitspunkt ρ
i
linearisierten Regelstrecke besteht. F
¨
ur die Regler kommen
verschiedene Reglertypen in Frage, z. B. lineare Zustandsregler, PID-Regler
usw.
Nach dem Entwurf der p Regler wird in einem letzten Entwurfsschritt
zwischen jeweils zwei benachbarten Reglern i und j ausgew
¨
ahlt bzw. inter-
poliert. Die Auswahl bzw. Interpolation erfolgt dabei in Abh
¨
angigkeit vom
168 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
Δw
i
Δu
i
Δx
i
Δy
i
Δy
i
˙z
i
= h
i
(z
i
, ..., Δw
i
)
Δu
i
= k
i
(z
i
, ..., Δw
i
)
Δ ˙x
i
=A(ρ
i
)Δx
i
+B(ρ
i
)Δu
i
Δy
i
= C(ρ
i
)Δx
i
Bild 4.2: Der i-te Regelkreis einer Gain-scheduling-Regelung.
Parametervektor ρ. Allerdings ist der Vektor ρ nicht in jedem Anwendungs-
fall bestimmbar oder messbar. Man ersetzt ihn dann durch einen Vektor β(t),
Schedulingvektor genannt, wobei sich dessen Elemente β
k
(t) aus bekannten
Gr
¨
oßen zusammensetzen wie
(1) den Zustandsvariablen x
k
,
(2) den Ausgangsvariablen y
k
,
(3) den Stellgr
¨
oßen u
k
,
(4) den Reglerzust
¨
anden z
k
oder
(5) den Sollgr
¨
oßen w
k
.
Dabei soll
l =dimρ =dimβ
und im station
¨
aren Fall
β
s
= β(t →∞)=ρ (4.1)
gelten.
DieeinfachsteM
¨
oglichkeit, die Stellgr
¨
oße u zu generieren, ist die Aktivie-
rung eines einzelnen Reglers i mit der Stellgr
¨
oße
u = u
R
(ρ
i
)+Δu
i
. (4.2)
Dabei wird der Regler i durch die Gleichung
i =argmin
k
||β − ρ
k
|| (4.3)
bestimmt. Aktiv ist somit jener Regler i, dessen Parametervektor ρ
i
dem
aktuellen Schedulingvektor β am n
¨
achsten liegt.
Das Regelgesetz (4.2) ist zwar einfach, besitzt aber den Nachteil, dass zwi-
schen den Reglern i mittels des Auswahlgesetzes (4.3) umgeschaltet wird. Un-
erw
¨
unschte Spr
¨
unge im Stellgr
¨
oßenverlauf, die das Stellglied nicht ausf
¨
uhren
oder verkraften kann, sind die Folge.
Sinnvoller ist es daher, ein Regelgesetz zu verwenden, das zwischen den
Reglern i,d.h.ihrenStellgr
¨
oßenwerten, interpoliert. Zusammengesetzt wird
die Stellgr
¨
oße dann anteilig aus den Werten u
R
(ρ
i
) und Δu
i
.Undzwarso,
dass zwischen den Reglern i, in deren G
¨
ultigkeitsbereich sich der Scheduling-
vektor β befindet, interpoliert wird.

4.1. Gain-scheduling-Regler 169
Die Interpolation zwischen den Stellgr
¨
oßen u
R
(ρ
i
)+Δu
i
der einzelnen
Regler erfolgt z. B. auf Basis des gewichteten Mittelwertes, der die Gleichung
des Gain-scheduling-Reglers
u =
p
i=1
μ
i
(β) · (u(ρ
i
)+Δu
i
)
p
i=1
μ
i
(β)
(4.4)
liefert. Die Gewichtungsfunktionen 0 ≤ μ
i
(β) ≤ 1 sind im Arbeitspunkt
β = ρ
i
identisch eins und nehmen zum Rand des G
¨
ultigkeitsbereiches, der zu diesem
Arbeitspunkt geh
¨
ort, stetig bis auf null oder n
¨
aherungsweise null ab. Eine
Funktion, die diese Eigenschaft besitzt, ist beispielsweise die mehrdimensio-
nale Gauß-Funktion
μ
i
(β)=e
−||Σ(β−ρ
i
)||
2
. (4.5)
Die l × l Matrix Σ ist z. B. eine Diagonalmatrix
Σ =
⎡
⎢
⎢
⎢
⎣
1
2σ
2
1
··· 0
.
.
.
.
.
.
.
.
.
0 ···
1
2σ
2
l
⎤
⎥
⎥
⎥
⎦
.
Durch die Matrix Σ erh
¨
alt jede Koordinatenrichtung des Schedulingvektors
β eine eigene Skalierung mittels 1/(2σ
2
j
). So k
¨
onnen nicht nur, wie in Bild 4.1,
Kreise als Niveaulinien der Funktion (4.5) ausgeformt werden, sondern auch
Ellipsen.
Normalerweise legt man die Funktionen μ
i
(β) durch geeignete Wahl von
σ
k
so aus, dass sie f
¨
ur β = ρ
j
mit i = j alle nahezu null und mit i = j
identisch eins sind. Dann reduziert sich f
¨
ur i = j Gl. (4.4) auf
u ≈
μ
i
(ρ
i
) · (u
R
(ρ
i
)+Δu
i
)
μ
i
(ρ
i
)
= u
R
(ρ
i
)+Δu
i
, (4.6)
d. h., im Arbeitspunkt i wird nur der zu ihm geh
¨
orige Regler Δu
i
aktiv.
Zwischen den Arbeitspunkten dagegen wird ein gewichteter Mittelwert der
einzelnen Reglerausgangsgr
¨
oßen u
R
(ρ
i
)+Δu
i
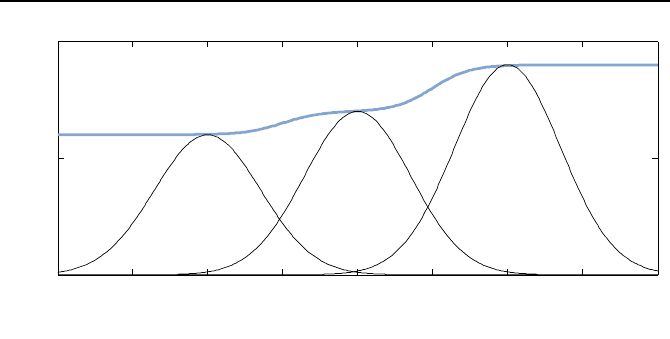
gebildet. Bild 4.3 illustriert
dies.
Das Interpolationsgesetz (4.4) besitzt die oftmals g
¨
unstige Eigenschaft,
dass f
¨
ur den Fall eines Vektors β, der außerhalb der betrachteten g
¨
ultigen
170 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
00.5
1
1.5
2
2.533.5
4
1
0.5
0
β
u
i =1
i =2
i =3
Bild 4.3: Die Interpolation u der Reglerausgangswerte u
R
(ρ
i
)+Δu
i
auf Basis des
gewichteten Mittelwertes ist als blaue Kurve exemplarisch dargestellt. Die schwarzen
Kurven entsprechen den Funktionen μ
i
(β) · (u
R
(ρ
i
)+Δu
i
)f
¨
ur i =1,...,3.
Arbeitsbereiche liegt, der Regler des zu β naheliegendsten Arbeitspunktes
aktiv bleibt. Dies l
¨
asst sich aus Gl. (4.4) erkennen, denn f
¨
ur solche Vektoren
β gilt
μ
i
(β) 1
f
¨
ur alle i. Dann besitzt der gr
¨
oßte dieser Werte, d. h. derjenige mit dem kleins-
ten euklidischen Abstand ||β − ρ
i
||,dengr
¨
oßten Einfluss in Gl. (4.4). Auch
in diesem Fall gilt dann wieder Gl. (4.6). Bild 4.3 illustriert auch diese Eigen-
schaft.
Insgesamt gesehen ist der Entwurf eines Gain-scheduling-Reglers in vier
Schritten darstellbar:
Schritt 1: Berechne die parametrierte Linearisierungsfamilie.
Schritt 2: Entwerfe die linearen Teilregler mittels linearer Entwurfsmethoden.
Schritt 3: Lege das Auswahl- bzw. Interpolationsgesetz f
¨
ur die Teilregler in
Abh
¨
angigkeit der Schedulingparameter fest.
Schritt 4: Simuliere den gesamten Regelkreis und pr
¨
ufe Stabilit
¨
at und Re-
gelg
¨
ute.
Insbesondere Schritt 4 bedarf der Beachtung, denn die Stabilit
¨
at kann
im Allgemeinen nicht analytisch gesichert werden. Die Stabilit
¨
at der linearen
Teilregelkreise ist hier nicht ausreichend, da das gesamte System nichtlinear
ist.
Erweiterungen und zus
¨
atzliche Betrachtungen zu Gain-scheduling-Reglern
finden sich in [8, 37, 43, 111, 192, 202]. Einen
¨
Uberblick bieten beispielsweise
[1, 112, 159].
4.1. Gain-scheduling-Regler 171
4.1.2 Illustrationsbeispiel
Es wird ein einfaches Beispiel betrachtet:
˙x = −x
3
+ u.
Das System hat die Ruhelage
x
R
=
3
√
u
R
.
Als Parameter ρ w
¨
ahlt man
ρ = u
R
.
So ergibt sich f
¨
ur die parametrierte Linearisierungsfamilie
Δ ˙x = AΔx + bΔu =
∂f(x, u
R
)
∂x
x
R
· Δx +
∂f(x
R
,u)
∂u
u
R
· Δu
= −3x
2
R
Δx + Δu = −3
3
1
u
2
R
Δx + Δu.
Man w
¨
ahlt des Weiteren f
¨
unf Arbeitspunkte aus mit
ρ
1
= u
R1
= −2,x
R1
= −
3
√
2 ≈−1.26,
ρ
2
= u
R2
= −1,x
R2
= −
3
√
1=−1,
ρ
3
= u
R3
=0,x
R3
=
3
√
0= 0,
ρ
4
= u
R4
=1,x
R4
=
3
√
1= 1,
ρ
5
= u
R5
=2,x
R5
=
3
√
2 ≈ 1.26
und
Δu
i
= u − u
Ri
sowie Δx
i
= x − x
Ri
.
Soergebensichf
¨
unf linearisierte Modelle mit
ρ
1
= u
R1
= −2 und Δ ˙x
1
= −4.76Δx
1
+ Δu
1
,
ρ
2
= u
R2
= −1 und Δ ˙x
2
= −3.00Δx
2
+ Δu
2
,
ρ
3
= u
R3
= 0 und Δ ˙x
3
= Δu
3
,
ρ
4
= u
R4
= 1 und Δ ˙x
4
= −3.00Δx
4
+ Δu
4
,
ρ
5
= u
R5
= 2 und Δ ˙x
5
= −4.76Δx
5
+ Δu
5
.
F
¨
ur jedes Modell wird nun ein P-Regler mit der Regelabweichung
Δe
i
= Δw
i
− Δx
i
und
Δu
i
= k
i
Δe
i
entworfen, so dass die jeweiligen Regelkreise die Eigenwerte
λ
1
= −12,λ
2
= −4.5,λ
3
= −1.5,λ
4
= −4.5,λ
5
= −12

172 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
aufweisen. Es ergeben sich folgende Teilregler Δu
i
= k
i
Δe
i
mit
k
1
=7.24,k
2
=1.50,k
3
=1.50,k
4
=1.50,k
5
=7.24.
Als Regelgesetz, f
¨
ur das wir die umschaltende Variante w
¨
ahlen, ergibt sich so
insgesamt mit den Gl. (4.2) und (4.3)
u = u
R
(ρ
i
)+Δu
i
= u
Ri
+ Δu
i
= u
Ri
+ k
i
· Δe
i
mit
i =arg min
k=1,...,5
|β − u
Rk
|.
W
¨
ahlt man im obigen Regelgesetz als Schedulingparameter
β = ρ = u,
so ist das Regelgesetz implizit in u. Dies ist ung
¨
unstig. Eine geeignetere Wahl
ergibt sich, wenn man, durch die Ruhelagengleichung
˙x = −x
3
+ u =0 ⇔ u = x
3
motiviert,
β = x
3
w
¨
ahlt. Offensichtlich ist dann die Bedingung (4.1), d. h. β
s
= ρ f
¨
ur den stati-
on
¨
aren Fall, erf
¨
ullt.
Bild 4.4 zeigt den kompletten Regelkreis. Es gilt
w
Ri
= x
Ri
und
Δe
i
= Δw
i
− Δx
i
= w − x = Δe.
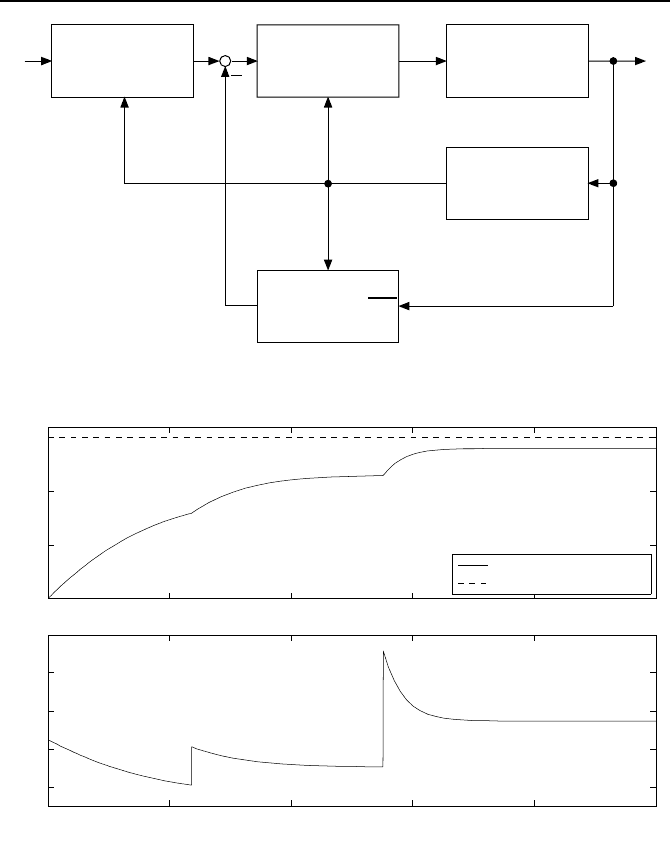
Bild 4.5 zeigt die Simulation des Regelkreisverhaltens f
¨
ur einen F
¨
uhrungs-
gr
¨
oßensprung von w =1.5. Da wir nur einen P-Regler verwenden, existiert eine
bleibende Regelabweichung. Die Unstetigkeiten im Verlauf von u kennzeichnen
einen Wechsel des Index i und damit auch einen Wechsel von
u = u
Ri
+ Δu
i
.
Wie erw
¨
ahnt, ist das oftmals unerw
¨
unscht, da nicht jedes Stellglied solche
Spr
¨
unge ausf
¨
uhren kann. Aber auch die abrupte
¨
Anderung im Verlauf der
Zustandsgr
¨
oße x ist, wenn man z. B. an eine Flugregelung denkt, nicht erstre-
benswert. In vielen F
¨
allen wird man sich glatte Verl
¨
aufe von Stellgr
¨
oßen und
Zustandsgr
¨
oßen w
¨
unschen.
Im n
¨
achsten Abschnitt betrachten wir ein Beispiel, bei dem zwischen den
Reglern interpoliert wird, so dass keine Spr
¨
unge im Stellgr
¨
oßenverlauf auftre-
ten.
4.1. Gain-scheduling-Regler 173
w
Δe
u
x
x
i
Δw
i
= w − w
Ri
u = u
Ri
+ k
i
Δe
˙x = −x
3
+ u
arg min
k
|x
3
−u
Rk
|
Δx
i
= x −
3
√
u
Ri
Bild 4.4: Strukturbild des kompletten Regelkreises.
0
0.5
1.5
1
1
2
3
4
5
0
0
0.5
0.5
1
1
1.5
1.5
2
2
2.5
2.5
Zeit t
ux
Zustandsgr
¨
oße x
F
¨
uhrungsgr
¨
oße w
Bild 4.5: Simulation von Zustandsgr
¨
oße x und Stellgr
¨
oße u der Gain-scheduling-
Regelung der Regelstrecke ˙x = −x
3
+ u.
4.1.3 Beispiel Solarkraftwerk mit Parabolrinnenkollektor
Wir betrachten das Parabolrinnenkraftwerk Acurex in Almer´ıa im S
¨
uden Spa-
niens [28, 85, 158]. Das Kraftwerk besitzt 480 Solarkollektoren, die bei einer
Sonneneinstrahlung von 900 W m
−2
eine elektrische Leistung von 1.2MWer-
zeugen. Hierbei fokussieren Parabolrinnen
¨
uber ihre verspiegelte Oberfl
¨
ache

174 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
die Sonnenstrahlen in einer lichtdurchl
¨
assigen Leitung, in der
¨
Ol zirkuliert.
Durch die geb
¨
undelten Sonnenstrahlen wird das
¨
Ol erhitzt und fließt dann in
einen isolierten Speichertank mit einem Volumen von 140 m
3
. Von hier aus
gelangt das
¨
Ol
¨
uber eine Pumpe zu einem Dampferzeuger, in dem die W
¨
arme
des
¨
Ols genutzt wird, um Wasserdampf zu erzeugen. Mit diesem wird schließ-
lich eine Turbine und ein elektrischer Generator betrieben. Das
¨
Ol wird nach
dem Verlassen des Dampferzeugers mit einer Rate von 2 bis 10 l s
−1
zur
¨
uck
in die Leitungen des Kollektorfeldes gepumpt. Das
¨
Ol kreist also st
¨
andig in
der Anlage. Bild 4.6 zeigt den prinzipiellen Aufbau des Systems.
Die Austrittstemperatur T
a
des
¨
Ols ist ein Maß f
¨
ur die aufgefangene Ener-
gie. Beschreiben l
¨
asst sich die Austrittstemperatur beim Verlassen des Kol-
lektorfeldes n
¨
aherungsweise
¨
uber die Leistungsbilanz
C
˙
T
a
= η
0
SJ − qp
cp
(T
a
− T
e
). (4.7)
Dabei ist T
e
die Temperatur des
¨
Ols beim Eintritt in das Kollektorfeld. Sie ist
konstant bzw.
¨
andert sich nur sehr langsam und geringf
¨
ugig. Die St
¨
arke der
Sonneneinstrahlung ist durch die Variable J ber
¨
ucksichtigt, wobei 0 ≤ J ≤
1kWm
−2
gilt. Im Gegensatz zu J kann der Volumenstrom q des
¨
Ols durch die
Pumpleistung zwischen 2 und 10 l s
−1
vorgegeben werden. Des Weiteren ist η
0
der optische Wirkungsgrad der Kollektoren, S die wirksame Kollektorfl
¨
ache,
C die W
¨
armekapazit
¨
at des
¨
Ols und p
cp
eine Systemkonstante. F
¨
ur die Acurex-
Anlage in Almer´ıa gilt
η
0
S = 1322 m
2
,
C = 2267 kJ
◦
C
−1
,
p
cp
=1.924 kJ
◦
C
−1
l
−1
.
Pumpe
T
e
q
Tank
zur
Turbine
T
a
Bild 4.6: Solarkraftwerk.

4.1. Gain-scheduling-Regler 175
Die
¨
Oltemperatur T
a
darf die Temperatur von 305
◦
Cnicht
¨
uberschreiten
und insbesondere darf die Differenz zwischen der Eintrittstemperatur T
e
und
der Austrittstemperatur T
a
nicht mehr als 100
◦
C betragen. Normale Werte
f
¨
ur diese Differenz liegen um 70
◦
C. Ist die Temperaturdifferenz T
a
−T
e
zu groß,
so steigt der
¨
Oldruck in den Leitungen im Kollektorfeld stark an. Leckagen
k
¨
onnen die Folge sein.
Man ist daher bestrebt, die Temperaturdifferenz
ΔT = T
a
− T
e
auf dem konstanten Wert von 70
◦
C zu halten. Dies geschieht mittels einer
Regelung, die
¨
uber den Volumenstrom q des
¨
Ols in Gl. (4.7) bzw. in der
Gleichung
C(ΔT )˙ + C
˙
T
e
= η
0
SJ − qp
cp
ΔT (4.8)
die Temperatur T
a
und damit ΔT beeinflusst. Da die Eintrittstemperatur T
e
n
¨
aherungsweise konstant ist bzw. sich nur sehr langsam
¨
andert, d. h.
˙
T
e
≈ 0,
k
¨
onnen wir f
¨
ur Gl. (4.8) die N
¨
aherung
C(ΔT )˙ = η
0
SJ − qp
cp
ΔT (4.9)
ansetzen.
Wir sind konformistisch und bezeichnen den Zustand ΔT des Systems
(4.9) mit x und seine Stellgr
¨
oße q mit u. So gilt
˙x = aJ − bxu (4.10)
mit a = η
0
SC
−1
=0.5831
◦
Cm
2
kJ
−1
und b = p
cp
C
−1
=0.8487 · 10
−3
l
−1
.
Dabei wirkt die St
¨
arke J der Sonneneinstrahlung aus regelungstechnischer
Sicht als St
¨
orgr
¨
oße.
Die Ruhelagen x
R
des Systems (4.8) sind durch
x
R
=
aJ
R
bu
R
(4.11)
gegeben. Die Temperaturdifferenz x
R
ist also proportional zur messbaren
St
¨
arke J der Sonneneinstrahlung. Im Falle einer konstanten Temperaturdiffe-
renz x
R
=70
◦
C gilt mit Gl. (4.11)
u
R
=9.82J
R
.
Wir wollen das System (4.10),
¨
ahnlich wie in [85], mittels Gain-scheduling
regeln. Zu diesem Zweck ermitteln wir zuerst die parametrierte Linearisie-
rungsfamilie
Δ ˙x =
∂aJ
∂J
J=J
R
· ΔJ −
∂bxu
R
∂x
x=x
R
· Δx −
∂bx
R
u
∂u
u=u
R
· Δu, (4.12)
