J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.


196 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
Mit den Zustandsvariablen
x
1
= h, x
2
=
˙
h und x
3
= m
sowie der Stellgr
¨
oße
u = − ˙m
erhalten wir mit Gl. (4.38) das Modell
⎡
⎢
⎢
⎣
˙x
1
˙x
2
˙x
3
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
x
2
−g
0
⎤
⎥
⎥
⎦
a(x)
+
⎡
⎢
⎢
⎣
0
v/x
3
−1
⎤
⎥
⎥
⎦
b(x)
u, (4.39)
y = c(x)=x
1
f
¨
ur die Landephase der F
¨
ahre. Man beachte, dass u = − ˙m immer positiv ist.
g
v
h
Bild 4.13: Mondlandef
¨
ahre Eagle der Apollo 11 Mission.

4.2. Reglerentwurf mittels exakter Linearisierung 197
Dem Entwurfsschema aus Abschnitt 4.2.5 folgend bestimmen wir
L
0
a
c(x)=c(x)=x
1
,
L
1
a
c(x)=
∂c(x)
∂x
a(x)=x
2
,
L
2
a
c(x)=
∂L
a
c(x)
∂x
a(x)=−g.
Des Weiteren berechnen wir
L
b
c(x)=
∂c(x)
∂x
b(x)=0,
L
b
L
a
c(x)=
∂L
a
c(x)
∂x
b(x)=
v
x
3
.
Da L
b
L
a
c(x) = 0 ist, besitzt das System den relativen Grad δ =2.Weil
die Systemordnung n =3>δist, verf
¨
ugt das System also
¨
uber eine in-
terne Dynamik. Die Masse x
3
= m der F
¨
ahre ist immer positiv und somit
gilt L
b
L
a
c(x)=v/x
3
> 0. Wir k
¨
onnen daher einen Regler mittels exakter
Linearisierung entwerfen. Dabei m
¨
ussen wir auch die Stabilit
¨
at der internen
Dynamik sicherstellen.
Wir schreiben f
¨
ur den Diffeomorphismus
z = t(x)=
⎡
⎢
⎢
⎣
c(x)
L
a
c(x)
t
3
(x)
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
x
1
x
2
t
3
(x)
⎤
⎥
⎥
⎦
,
wobei die Funktion t
3
(x)nochzuw
¨
ahlen ist. Dies geschieht so, dass die par-
tielle Differenzialgleichung (4.31), d. h. im vorliegenden Fall
L
b
t
3
(x)=
∂t
3
(x)
∂x
b(x)=0,
erf
¨
ullt ist. Konkret gilt
L
b
t
3
(x)=
∂t
3
(x)
∂x
2
·
v
x
3
−
∂t
3
(x)
∂x
3
=0. (4.40)
Diese partielle Differenzialgleichung besitzt die L
¨
osung
t
3
(x)=x
3
· e
x
2
/v
,
was leicht durch Einsetzen in Gl. (4.40) zu
¨
uberpr
¨
ufen ist. Der Diffeomorphis-
mus besitzt dann die Gestalt
z = t(x)=
⎡
⎢
⎢
⎣
x
1
x
2
x
3
e
x
2
/v
⎤
⎥
⎥
⎦
bzw. x = t
−1
(z)=
⎡
⎢
⎢
⎣
z
1
z
2
z
3
e
−z
2
/v
⎤
⎥
⎥
⎦
. (4.41)

198 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
Die Systembeschreibung mit externer und interner Dynamik errechnet sich
mit Gl. (4.39) und Gl. (4.41) zu
⎡
⎢
⎢
⎣
˙z
1
˙z
δ=2
˙z
3
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
L
a
c(x)
L
2
a
c(x)+L
b
L
a
c(x)u
˙
t
3
(x
2
,x
3
)
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
x
2
−g + vu/x
3
−v
−1
gx
3
e
x
2
/v
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
z
2
−g + vu/x
3
−v
−1
gz
3
⎤
⎥
⎥
⎦
.
⎫
⎬
⎭
externe Dynamik
} interne Dynamik
(4.42)
Wir entwerfen nun das Regelgesetz gem
¨
aß Satz 19 zu
u = −
L
2
a
c(x)+a
1
L
a
c(x)+a
0
c(x)
L
b
L
a
c(x)
= −
−g + a
1
x
2
+ a
0
x
1
v
x
3
= −
−g + a
1
z
2
+ a
0
z
1
v
x
3
. (4.43)
Eine F
¨
uhrungsgr
¨
oße w ist nicht erforderlich, da wir x
1
= z
1
und x
2
= z
2
in
die Ruhelage [x
1R
x
2R
]
T
= 0 ausregeln. Daher entf
¨
allt das Vorfilter v(x).
Das gesamte geregelte System wird nun mit den Gl. (4.41), (4.42), (4.43)
durch
⎡
⎢
⎢
⎣
˙z
1
˙z
2
˙z
3
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
z
2
−a
1
z
2
− a
0
z
1
−v
−1
gz
3
⎤
⎥
⎥
⎦
, (4.44)
y = z
1
beschrieben. Wie man in dieser Darstellung sieht, sind interne und externe
Dynamik entkoppelt. Insbesondere bereitet die interne Dynamik keine Pro-
bleme, denn sie ist stabil. Man erkennt auch, dass die interne Dynamik nicht
beobachtbar ist, da z
3
nicht auf y = z
1
wirkt.
Wir transformieren das Systemverhalten der Anschauung halber noch in
die Originalkoordinaten x zur
¨
uck und erhalten mit Gl. (4.44) und dem Dif-
feomorphismus (4.41) die Darstellung des Regelungssystems in der Form
⎡
⎢
⎢
⎣
˙x
1
˙x
2
˙x
3
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
x
2
−a
1
x
2
− a
0
x
1
v
−1
x
3
(a
1
x
2
+ a
0
x
1
− g)
⎤
⎥
⎥
⎦
.
Auch in dieser Gleichung erkennt man, dass die interne Dynamik die geregelte
externe nicht beeinflusst.
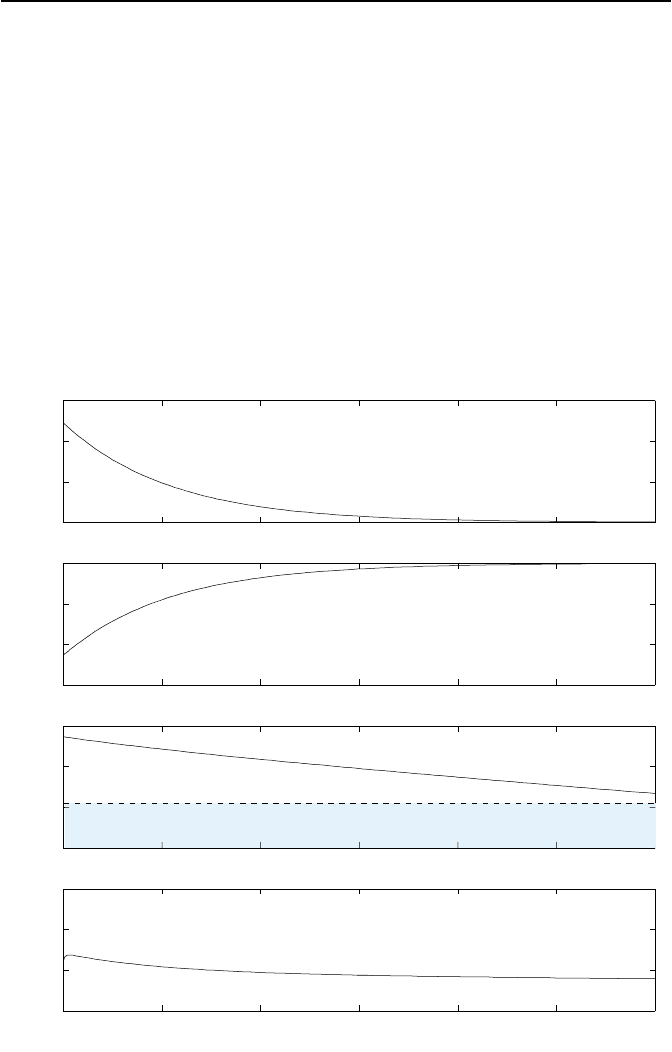
4.2. Reglerentwurf mittels exakter Linearisierung 199
Als konkretes Zahlenbeispiel betrachten wir die Mondf
¨
ahre Eagle und si-
mulieren, siehe Bild 4.14, die Ann
¨
aherungs- und Landephase auf dem Mond
mittels des entworfenen Reglers (4.43). Wir w
¨
ahlen die Koeffizienten a
0
=0.02
und a
1
=1.1, so dass die Eigenwerte der geregelten externen Dynamik bei
λ
1
= −0.0185 und λ
2
= −1.0815 liegen. So ergibt sich mit g =1.62 m s
−2
und v = 3050 m s
−1
als Modell der geregelten F
¨
ahre
⎡
⎢
⎢
⎣
˙x
1
˙x
2
˙x
3
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
x
2
−1.1x
2
− 0.02x
1
x
3
(3.61 · 10
−4
x
2
+6.56 · 10
−6
x
1
− 5.31 · 10
−4
)
⎤
⎥
⎥
⎦
.
Wir starten die Ann
¨
aherungs- und Landephase [9] in x
1
(0) = 2450 m
H
¨
ohe bei einer Sinkgeschwindigkeit von x
2
(0) = −45 m s
−1
. Der Treibstoff-
Zeit t in s
x
1
in m
x
2
in m s
−1
x
3
in t
u in kg s
−1
3000
2000
1000
15
10
5
0
0
0
-20
-40
-60
7
8
9
6
0
0
0
0
50
50
50
50
100
100
100
100
150
150
150
150
200
200
200
200
250
250
250
250
300
300
300
300
Gewicht der Mondlandef
¨
ahre ohne Treibstoff
Bild 4.14: H
¨
ohe x
1
, Geschwindigkeit x
2
, Gesamtmasse x
3
und Stellgr
¨
oße u.

200 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
vorrat betr
¨
agt zu diesem Zeitpunkt noch 1633 kg. Die Gesamtmasse ist somit
x
3
(0) = 8732 kg. Wir gehen davon aus, dass die Bewegung der F
¨
ahre in dieser
Phase n
¨
aherungsweise vertikal zur Mondoberfl
¨
ache stattfindet. (In der Rea-
lit
¨
at war dieser Kurs der F
¨
ahre in der letzten Phase der Landung aufgrund des
um einen Teil des Mondes herumf
¨
uhrenden Abstiegsorbits noch nicht v
¨
ollig
senkrecht.) Die Verl
¨
aufe der H
¨
ohe x
1
, der Geschwindigkeit x
2
und der verblei-
benden Gesamtmasse x
3
zeigt Bild 4.14.
4.3 Control-Ljapunov-Funktionen
4.3.1 Grundlagen
Die direkte Methode von Ljapunov wird neben der Stabilit
¨
atsanalyse auch
f
¨
ur die Reglersynthese verwendet. Ein solches Reglersyntheseverfahren ba-
siert zum Beispiel auf Control-Ljapunov-Funktionen V (x), abgek
¨
urzt CLF,
bei denen mittels des Stellgr
¨
oßenvektors u einer nichtlinearen Regelstrecke
˙x = f(x, u)
mit der einen Ruhelage x
R
= 0 die Ableitung
˙
V (x)=f
T
(x, u) · grad V (x)
einer Ljapunov-Funktion V (x) so minimiert wird, dass
˙
V (x) < 0
f
¨
ur alle x = 0 ist. Man bestimmt also z. B. u so, dass das Infimum
inf
u
/
˙
V (x)=f
T
(x, u) · grad V (x)
0
,
d. h. die untere Grenze von
˙
V (x), f
¨
ur alle x = 0 kleiner als null ist. Die
ermittelte Stellgr
¨
oße u(x) bildet dann ein Regelgesetz, das zu einem Regelkreis
˙x = f (x, u(x))
mit der global asymptotisch stabilen Ruhelage x
R
= 0 f
¨
uhrt.
Um die Stabilit
¨
at des Regelkreises sicherzustellen, muss man nicht un-
bedingt dasjenige u(x) als Regelgesetz w
¨
ahlen, das das Infimum von
˙
V (x)
erzeugt. Vielmehr reicht ein u(x), das zu
˙
V (x) < 0f
¨
ur alle x f
¨
uhrt. Die
Wahl des Reglers u(x), der zum infimalen
˙
V f
¨
uhrt, hat allerdings den Vorteil,
dass V (x) entlang der Trajektorien x(t) schnell abnimmt und somit auch die
Ausregelung schnell ist. Aus der Tatsache, dass wir mittels einer Ljapunov-
Funktion einen die Stabilit
¨
at sichernden Regler u(x) festlegen, leitet sich der
Name Control-Ljapunov-Funktion ab.
F
¨
ur zeitinvariante nichtlineare Systeme ist der Begriff der Control-Ljapu-
nov-Funktion wie folgt definiert.

4.3. Control-Ljapunov-Funktionen 201
Definition 11 (Control-Ljapunov-Funktion). Gegeben sei das System
˙x = f (x, u), x ∈ IR
n
, u ∈ IR
m
,
mit der Ruhelage x
R
= 0 f
¨
ur u = 0. Dann heißt eine stetig differenzierbare
Funktion V (x) Control-Ljapunov-Funktion, wenn sie die folgenden Bedingun-
gen erf
¨
ullt:
(1) V (0)=0
(2) V (x) > 0 f
¨
ur alle x = 0
(3) V (x) →∞ f
¨
ur |x|→∞
(4) Es gibt ein u(x), so dass
˙
V (x) < 0 f
¨
ur alle x = 0 gilt.
Wenn wir den Satz von Barbashin und Krasovskii, d. h. Satz 10, nutzen,
k
¨
onnen wir den Begriff der Control-Ljapunov-Funktion etwas weniger restrik-
tiv definieren. Wir erhalten so die erweiterte
Definition 12 (Erweiterte Control-Ljapunov-Funktion). Gegeben sei
das System
˙x = f (x, u), x ∈ IR
n
, u ∈ IR
m
,
mit der Ruhelage x
R
= 0 f
¨
ur u = 0. Dann heißt eine stetig differenzierbare
Funktion V (x) erweiterte Control-Ljapunov-Funktion, wenn sie die folgenden
Bedingungen erf
¨
ullt:
(1) V (0)=0
(2) V (x) > 0 f
¨
ur alle x = 0
(3) V (x) →∞ f
¨
ur |x|→∞
(4) Es gibt ein u(x), so dass
˙
V (x) ≤ 0 f
¨
ur alle x = 0 gilt.
(5) Die Menge von Zust
¨
anden x des mit u(x) geregelten Systems, f
¨
ur die
˙
V (x)=0gilt, enth
¨
alt keine Trajektorie x(t).
Definition 12 weicht die Forderung
˙
V (x) < 0 aus Definition 11 auf. Nun
k
¨
onnen wir auch den Fall
˙
V (x) ≤ 0f
¨
ur x = 0 nutzen, solange gem
¨
aß Bedin-
gung (5) entlang keiner Trajektorie x(t) des geregelten Systems
˙
V (x(t)) = 0
gilt.
Aufgrund der beiden Stabilit
¨
atss
¨
atze von Ljapunov und von Barbashin und
Krasovskii kann mittels obiger Definitionen folgender Satz direkt abgeleitet
werden.
Satz 20 (Existenz eines Regelgesetzes). Gegeben sei das System
˙x = f (x, u), x ∈ IR
n
, u ∈ IR
m
,
mit der Ruhelage x
R
= 0 f
¨
ur u = 0. Existiert dann eine Control-Ljapunov-
Funktion oder eine erweiterte Control-Ljapunov-Funktion V (x) f
¨
ur das Sys-
tem, so kann immer eine Regelung u(x) gefunden werden, so dass die Ruhe-
lage x
R
= 0 global asymptotisch stabil ist.

202 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
Ist Bedingung (3) der Definitionen 11 und 12 nicht erf
¨
ullt, so kann nur lokale
asymptotische Stabilit
¨
at sichergestellt werden.
Wie schon im Fall der Stabilit
¨
atsanalyse mit der direkten Methode, besteht
auch bei obigem Satz zur Reglersynthese die Hauptschwierigkeit in der Auffin-
dung einer geeigneten Ljapunov-Funktion V (x). Ein generelles Verfahren zur
Konstruktion einer solchen Ljapunov-Funktion existiert nicht. Man ist also
in vielen F
¨
allen auf seine Intuition oder auf das Ausprobieren verschiedener
Kandidatinnen f
¨
ur Ljapunov-Funktionen V (x) angewiesen.
4.3.2 Control-Ljapunov-Funktion f
¨
ur lineare Systeme
Als einfaches Beispiel betrachten wir zum Zwecke der Veranschaulichung die
Regelstrecke
˙x = Ax + bu, |u|≤u
max
,
mit einer stabilen Matrix A und
V (x)=x
T
Rx
als Kandidatin f
¨
ur eine Control-Ljapunov-Funktion. Es ergibt sich
˙
V (x)=x
T
A
T
R + RA
!
x +2b
T
Rx·u.
Offensichtlich ist V (x)=x
T
Rx eine Control-Ljapunov-Funktion, wenn
die Matrix
A
T
R + RA
negativ definit ist, denn mit
u = −u
max
sgn
b
T
Rx
!
(4.45)
und
sgn
b
T
Rx
!
b
T
Rx= |b
T
Rx|
ist die Bedingung (4) der Definition 11
˙
V (x)=f
T
(x,u)gradV (x)
= x
T
A
T
R + RA
!
x − 2u
max
|b
T
Rx| < 0
erf
¨
ullt.
Bei stabilen linearen Systemen ist eine Control-Ljapunov-Funktion also
einfach zu ermitteln. Allerdings hat dieses Regelgesetz den Nachteil, dass zwi-
schen −u
max
und +u
max
hin und her geschaltet wird. Nur wenige Stellglieder
k
¨
onnen die daf
¨
ur n
¨
otige Stellgeschwindigkeit aufbringen. Des Weiteren k
¨
onnen
unerw
¨
unschte Gleitzust
¨
ande entstehen.

4.3. Control-Ljapunov-Funktionen 203
4.3.3 Regler f
¨
ur eingangslineare Systeme
Nach diesem einfachen Beispiel betrachten wir einen allgemeineren Fall. Die
nun betrachteten Regelstrecken sind eingangslineare Systeme
˙x = a(x)+B(x) · u. (4.46)
Die Bedingung (4) der Definition 11 nimmt in diesem Fall die Form
a
T
(x) · V
x
(x)+u
T
B
T
(x) · V
x
(x) < 0 (4.47)
an. Dabei schreiben wir der
¨
Ubersicht halber den Gradienten der Control-
Ljapunov-Funktion V (x)abgek
¨
urzt mit
V
x
(x) = grad V (x).
Aus der Ungleichung (4.47) l
¨
asst sich direkt folgender Satz herleiten.
Satz 21 (Control-Ljapunov-Funktion f
¨
ur eingangslineare Systeme).
F
¨
ur ein System ˙x = a(x)+B(x)u ist V (x) eine Control-Ljapunov-Funktion,
wenn eine der Bedingungen
(1) B
T
(x)V
x
(x) = 0 f
¨
ur alle x ∈ IR
n
\{0},
(2) a
T
(x)V
x
(x) < 0 f
¨
ur x ∈
/
x | x ∈ IR
n
\{0} mit B
T
(x)V
x
(x)=0
0
,
a
T
(x)V
x
(x)=0 f
¨
ur x = 0
erf
¨
ullt ist.
Die Bedingung (2) in obigem Satz beinhaltet auch die Situation
a
T
(x)V
x
(x) < 0f
¨
ur x ∈ IR
n
\{0},
a
T
(x)V
x
(x)=0 f
¨
ur x = 0,
(4.48)
die den wichtigen Fall abdeckt, dass V bereits f
¨
ur das autonome System ˙x =
a(x) eine Ljapunov-Funktion ist.
F
¨
ur den Fall, dass eine Control-Ljapunov-Funktion V (x)f
¨
ur die Regel-
strecke ˙x = a(x)+B(x) · u bekannt ist, hat E. D. Sontag ein Regelgesetz
angegeben, das die Ruhelage x
R
= 0 des Systems global asymptotisch stabi-
lisiert [171]. Es gilt
Satz 22 (Sontags Regelgesetz). Sei V (x) eine Control-Ljapunov-Funk-
tion f
¨
ur das System ˙x = a(x)+B(x) · u mit dem Regelgesetz
u(x)=
2
−k
s
(x)B
T
(x)V
x
(x) f
¨
ur B
T
(x)V
x
(x) = 0,
0 f
¨
ur B
T
(x)V
x
(x)=0
mit
k
s
(x)=
a
T
(x)V
x
(x)+
1
(a
T
(x)V
x
(x))
2
+ h
2
(x)
h(x)
,
h(x)=V
x
T
(x)B(x)B
T
(x)V
x
(x),
dann besitzt der Regelkreis die global asymptotisch stabile Ruhelage x
R
=0.

204 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
Setzt man Sontags Regelgesetz in die Ungleichung (4.47) ein, so ist leicht
festzustellen, dass diese erf
¨
ullt ist.
Wir betrachten nun noch zwei Regelgesetze f
¨
ur den Fall, dass die Control-
Ljapunov-Funktion die Bedingung (4.48) und damit die Bedingung (2) des
Satzes 21 erf
¨
ullt. In diesem Fall ist der autonome Teil ˙x = a(x) des Systems
(4.46) stabil. Wir stellen das System (4.46) in der Form
˙x = a(x)+
m
i=1
b
i
(x) · u
i
dar, wobei die Vektoren b
i
(x) die Spaltenvektoren der Matrix B(x) sind.
Wir wollen annehmen, dass es uns gelungen ist, eine entsprechende Control-
Ljapunov-Funktion zu finden. Dann gilt
˙
V (x)=a
T
(x)V
x
(x)
< 0
+
m
i=1
V
x
T
(x)b
i
(x) · u
i
. (4.49)
Es ist sinnvoll, damit die Ausregelung einer Trajektorie x(t) in die Ruhe-
lage x
R
= 0 schnell geschieht, alle u
i
in Gl. (4.49) so zu w
¨
ahlen, dass
˙
V (x)
m
¨
oglichst hohe negative Werte annimmt. Im Falle von Stellgr
¨
oßenbeschr
¨
an-
kungen |u
i
|≤u
i,max
ist das der Fall, wenn man als Regelgesetz
u
i
= −u
i,max
sgn(V
x
T
(x)b
i
(x))
f
¨
ur i =1,...,m w
¨
ahlt. Denn dann gilt
˙
V (x)=a
T
(x)V
x
(x) −
m
i=1
u
i,max
V
x
T
(x)b
i
(x)
< 0.
Allerdings hat dieses schaltende Regelgesetz einen unstetigen Stellgr
¨
oßen-
verlauf und m
¨
oglicherweise unerw
¨
unschte Gleitzust
¨
ande. Beides sind Nachtei-
le, die auch schon im Fall des Regelgesetzes (4.45) auftraten.
Man vermeidet die obigen Nachteile, wenn man die Stellgr
¨
oße mittels einer
S
¨
attigungsfunktion zu
u
i
= −sat(V
x
T
(x)b
i
(x)), sat(v)=
⎧
⎪
⎨
⎪
⎩
v
max
,v>v
max
,
v, |v|≤v
max
,
−v
max
,v<−v
max
,
w
¨
ahlt. Somit erh
¨
alt man
˙
V (x)=a
T
(x)V
x
(x) −
m
i=1
V
x
T
(x)b
i
(x)sat(V
x
T
(x)b
i
(x)) < 0
und V nimmt auch in diesem Fall entlang einer jeden Trajektorie schnell ab.
4.3. Control-Ljapunov-Funktionen 205
4.3.4 Illustrationsbeispiel
Wir betrachten das Beispielsystem
˙
x =
⎡
⎣
−x
1
1 − e
−x
2
1
−x
2
2
!
+ x
2
e
−x
2
1
−x
2
2
−x
1
e
−x
2
1
−x
2
2
− x
2
1 − e
−x
2
1
−x
2
2
!
⎤
⎦
a(x)
+
⎡
⎣
10
01
⎤
⎦
B(x)
u
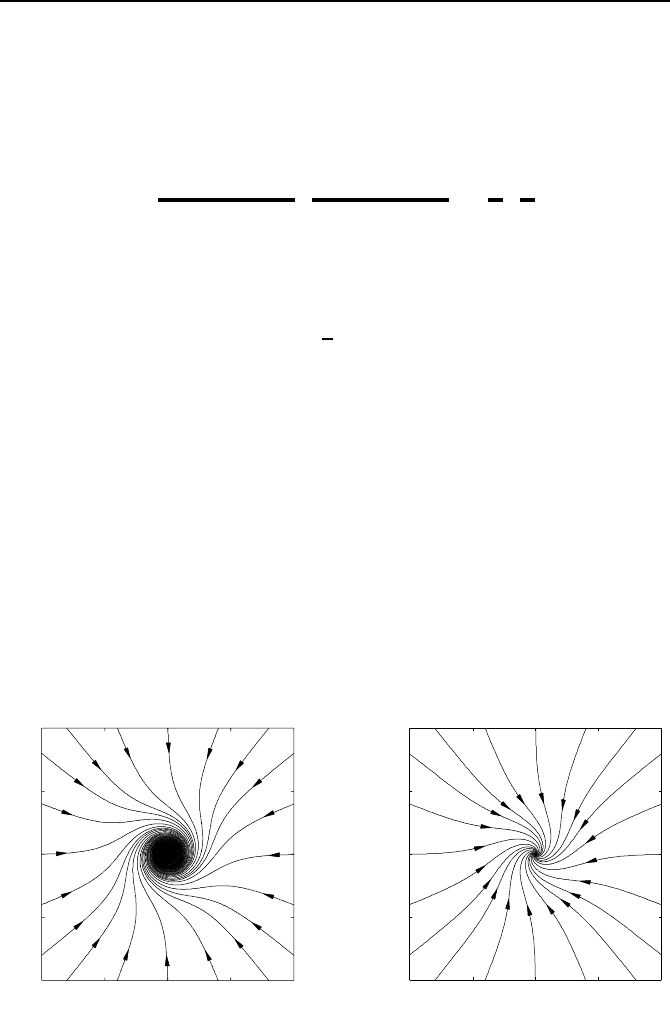
mit der Ruhelage x
R
= 0. Bild 4.15 zeigt die Trajektorienverl
¨
aufe des Systems
f
¨
ur u = 0. Als Kandidatin f
¨
ur eine Control-Ljapunov-Funktion setzt man
V (x)=
1
2
x
2
1
+ x
2
2
an. F
¨
ur den Gradienten erh
¨
alt man
V
x
T
(x)=
x
1
x
2
und somit
B
T
V
x
(x)=
x
1
x
2
.
Da B
T
V
x
(x) =0f
¨
ur alle x = 0 gilt, ist V gem
¨
aß Satz 21 eine Control-
Ljapunov-Funktion. Dies ist auch direkt aus
˙
V (x)=−
x
2
1
+ x
2
2
1 − e
−x
2
1
−x
2
2
!
+ x
1
u
1
+ x
2
u
2
x
1
x
2
-2
-1
0
1
2
-2
-1
0
1
2
Bild 4.15: Trajektorien des ungeregel-
ten Systems.
x
1
x
2
-2
-1
0
1
2
-2
-1
0
1
2
Bild 4.16: Trajektorien des geregelten
Systems.
