J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.

206 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
0.2
0
-0.2
0
2
4
6810
12 14
16 18 20
Zustand x
1
Zeit t
geregelt
ungeregelt
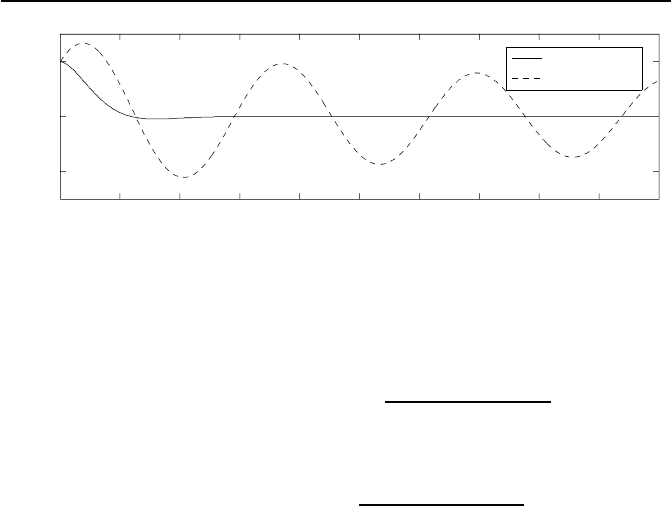
Bild 4.17: Verlauf der Zustandsgr
¨
oße x
1
im geregelten und ungeregelten Fall.
erkennbar.
Es ergibt sich aus Satz 22
k
s
(x)=−
1 − e
−x
2
1
−x
2
2
!
+
1
1 − e
−x
2
1
−x
2
2
2
+1
und Sontags Regelgesetz hat dann hier die Form
u(x)=
1 − e
−x
2
1
−x
2
2
!
−
1
1 − e
−x
2
1
−x
2
2
2
+1
x.
Das Bild 4.16 zeigt die Trajektorien des geregelten Systems und Bild 4.17
zeigt beispielhaft den Verlauf von x
1
f
¨
ur das ungeregelte und das geregelte
System bei einem Anfangswert von x(0) = [0.20.2]
T
. Gegen
¨
uber dem stark
schwingenden System besitzt der Regelkreis praktisch keine Schwingneigung
mehr.
4.3.5 Beispiel Kraftwerk mit Netzeinspeisung
Wir betrachten ein Kraftwerk zur Erzeugung elektrischer Energie, das
¨
uber
eine lange Hochspannungsleitung mit dem Energieversorgungsnetz verbunden
ist, und sein Verhalten nach einem Leitungskurzschluss [108, 133]. Das Ener-
gieversorgungsnetz wird dabei als starr angenommen, d. h., seine Frequenz
ist konstant und die Stabilit
¨
at des Netzes wird durch das betrachtete Kraft-
werk nicht beeinflusst. Wasserkraftwerke in entlegenen Regionen werden
¨
uber
solche langen Hochspannungsleitungen an das Energieversorgungsnetz ange-
schlossen. Auch Braunkohlekraftwerke, die in der N
¨
ahe der Kohlef
¨
orderung
liegen, k
¨
onnen so an das Netz angebunden sein, wie es Bild 4.18 illustriert.
Die Leitung kann dabei in Serie mit einem kapazitiven Widerstand X
C
geschaltet werden [62, 120, 176]. Diese Schaltung wird vor allem als Ersatz-
modell f
¨
ur die Kopplung von Netzen benutzt. Die Summe aus transientem
induktiven Generatorwiderstand, induktivem Transformator- und Leitungs-
widerstand ist X
L
.Und
¯
E = Ee
jδ
ist die Generatorspannung und
¯
V = Ve
j0
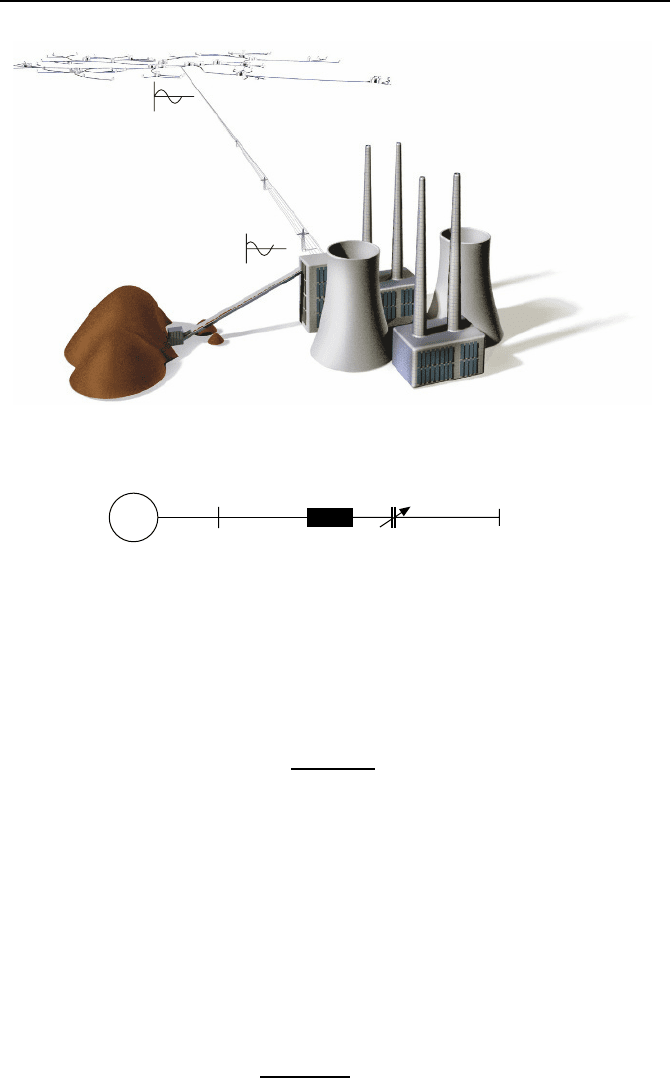
4.3. Control-Ljapunov-Funktionen 207
Bild 4.18: Kohlekraftwerk mit langer Verbindungsleitung zum starren Netz.
G
¯
E =E · e
jδ
X
L
X
C
¯
V = V · e
j0
starres Netz
Bild 4.19: Generator mit Verbindungsleitung zum Energieversorgungsnetz.
die Spannung des starren Netzes. Bild 4.19 zeigt das Ersatzschaltbild des Sys-
tems. Der Winkel δ setzt sich aus dem Polradwinkel des Synchrongenerators
und der Phasenverschiebung, die aus der Leitung resultiert, zusammen.
Die
¨
uber die Leitung transportierte Wirkleistung ist
P =
E · V
X
L
− X
C
sin δ. (4.50)
Nun wird auch die Bedeutung des zus
¨
atzlich in das System eingebrachten Kon-
densators deutlich. Er erh
¨
oht die
¨
uber die Leitung transportierbare Leistung
P , da er den Nenner X
L
− X
C
in Gl. (4.50) verringert.
Die Kapazit
¨
at hat eine weitere Funktion. Legt man sie ver
¨
anderlich mit
X
C
= X
C
0
+ ΔX
C
, (4.51)
aus, so kann man sie benutzen, um Systemst
¨
orungen nach einem Leitungs-
fehler, z. B. einem Kurzschluss, m
¨
oglichst schnell auszuregeln. Mit Gl. (4.51)
erh
¨
alt man f
¨
ur Gl. (4.50)
P =
E · V
X
L
− X
C
0
(1 + u)sinδ (4.52)
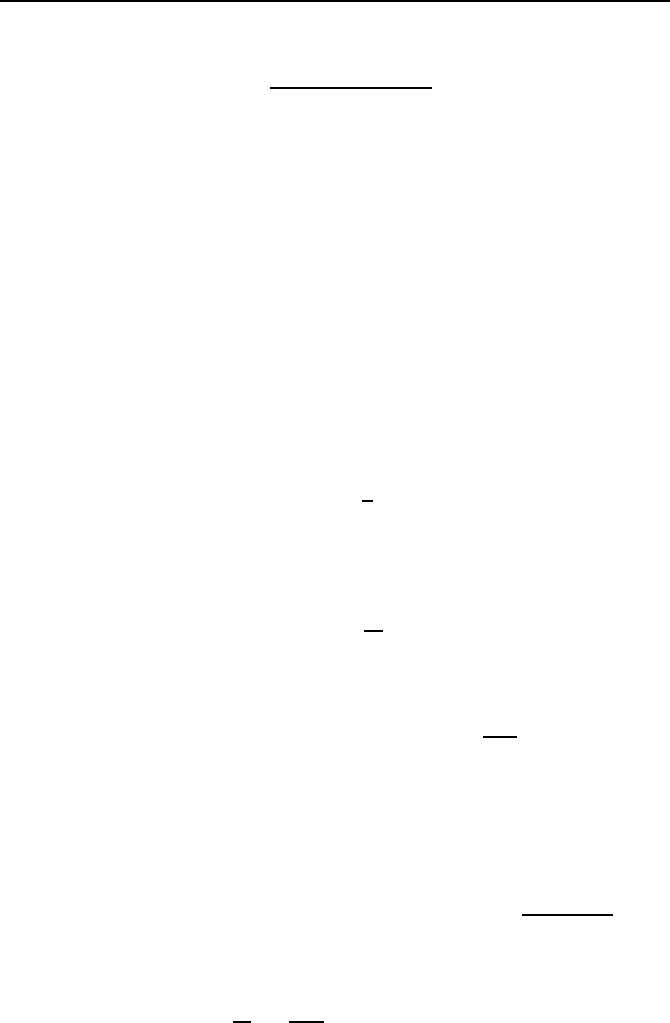
208 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
mit
u =
ΔX
C
X
L
− X
C
0
− ΔX
C
.
Im station
¨
aren Betrieb gilt f
¨
ur die mechanische Winkelgeschwindigkeit ω
m
des Polrades der Synchronmaschine mit der Polpaarzahl p und f
¨
ur die Fre-
quenz ω
e
der Polradspannung E sin (ω
e
t + δ) die Beziehung
ω
e
= pω
m
.
Treten zeitliche
¨
Anderungen des Winkels δ auf, z. B. aufgrund eines Leitungs-
kurzschlusses, so
¨
andert sich gezwungenermaßen die Frequenz der Polradspan-
nung E sin (ω
e
t + δ) und damit auch die mechanische Frequenz des Polrades
gem
¨
aß
ω
e
+
˙
δ = p(ω
m
+ Δω
m
).
Hieraus resultiert f
¨
ur die
¨
Anderung der mechanischen Frequenz des Polrades
Δω
m
=
˙
δ
p
.
Wir betrachten nun die Leistungsbilanz des Systems. Die Turbinenleistung
P
T
, vermindert um die d
¨
ampfende Verlustleistung
DΔω
m
=
D
p
˙
δ
und vermindert um die den Rotor beschleunigende bzw. bremsende Leistung
J(ω
m
+ Δω
m
)(Δω
m
)˙ ≈ Jω
m
(Δω
m
)˙ =
Jω
e
p
2
¨
δ,
ist gleich der vom Generator erzeugten und
¨
uber die Leitung transportierten
elektrischen Leistung P aus Gl. (4.52). Dabei ist D eine D
¨
ampfungskonstante
und J das Tr
¨
agheitsmoment aller rotierenden Teile von Turbine und Genera-
tor. Somit gilt
P
T
− DΔω
m
− Jω
m
(Δω
m
)˙ = P
E
(1 + u)sinδ, P
E
=
E · V
X
L
− X
C
0
,
f
¨
ur die Leistungsbilanz, woraus
P
T
−
D
p
˙
δ −
Jω
e
p
2
¨
δ = P
E
(1 + u)sinδ
bzw.
4.3. Control-Ljapunov-Funktionen 209
¨
δ =
p
2
Jω
e
P
T
−
D
p
˙
δ − P
E
(1 + u)sinδ
(4.53)
folgt.
Der station
¨
are Betriebspunkt des Systems ergibt sich mit
¨
δ = 0 und
˙
δ =0
sowie u = 0 aus Gl. (4.53) zu
δ
R
=arcsin
P
T
P
E
.
Der Winkel δ bewegt sich typischerweise in engen Grenzen um den Betriebs-
punkt δ
R
herum. Nur bei gr
¨
oßeren St
¨
orungen k
¨
onnen auch gr
¨
oßere Werte
δ ∈ [−π, π] auftreten.
¨
Anderungen des Winkels δ sind unerw
¨
unscht, denn
gem
¨
aß Gl. (4.52) schwankt dann die
¨
ubertragene elektrische Leistung P .Des
Weiteren kann bei großen
¨
Anderungen des Winkels δ der Synchrongenera-
tor außer Tritt geraten, d. h., das Polrad l
¨
auft nicht mehr synchron mit dem
Drehfeld des Stators.
Wir definieren als Zustandsvektor
x
1
x
2
=
δ − δ
R
˙
δ
und des Weiteren
a
1
=
p
2
P
T
Jω
e
,a
2
=
pD
Jω
e
und a
3
=
p
2
P
E
Jω
e
.
So erhalten wir aus Gl. (4.53) das Modell des an ein starres Netz angekoppel-
ten Kraftwerkes zu
˙x
1
˙x
2
=
x
2
a
1
− a
2
x
2
− a
3
(1 + u)sin(x
1
+ δ
R
)
. (4.54)
Dabei ist u die Stellgr
¨
oße des Systems. Das System (4.54) hat f
¨
ur u =0die
Ruhelagen
x
R2i
=
±2iπ
0
, x
R(2i+1)
=
±(2i +1)π − 2δ
R
0
f
¨
ur i =0, 1, 2,...
Da sich die Ruhelagen und die zugeh
¨
origen Trajektorienverl
¨
aufe f
¨
ur Indizes
i>0 periodisch aufgrund der Sinusfunktion in Gl. (4.54) wiederholen, ist es
ausreichend die Ruhelagen
x
R0
=
0
0
und x
R1
=
π − 2δ
R
0
zu betrachten. Mittels der indirekten Methode von Ljapunov, d. h. Satz 12,
l
¨
asst sich anhand des linearisierten Modells des Systems (4.54) leicht nachwei-
sen, dass die Ruhelage x
R0
stabil und die Ruhelage x
R1
instabil ist.
210 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
Ziel ist es, St
¨
orungen, die z. B. aufgrund von Leitungsfehlern entstehen, das
bedeutet hier x = 0, schnell auszuregeln. D. h., man m
¨
ochte Abweichungen
von der Ruhelage x
R0
schnell mittels einer Regelung eliminieren.
Zur Herleitung eines Regelgesetzes f
¨
ur das System (4.54) setzen wir die
Control-Ljapunov-Funktion
V (x)=
1
2
x
2
2
− a
1
x
1
+ a
3
(cos δ
R
− cos(δ
R
+ x
1
)) (4.55)
an. Es gilt V (0) = 0 und V (x) > 0 in einer Umgebung der Ruhelage x
R0
=
0. Die Control-Ljapunov-Funktion erf
¨
ullt allerdings nicht f
¨
ur gr
¨
oßere Werte
x
1
> 0 die Bedingung V (x) > 0. Dies ist auch nicht erforderlich, da große
Werte von x
1
= δ − δ
R
nicht auftreten. Bild 4.20 illustriert exemplarisch den
Verlauf der Funktion V (x). Dabei beschr
¨
anken wir uns auf den Fall x
2
=0,
denn nur f
¨
ur die von x
1
abh
¨
angige Komponente ist der Verlauf von V (x)nicht
direkt ersichtlich. Der Anteil 0.5x
2
2
dagegen hat die Form einer Parabel.
x
1
= δ − δ
R
V
80
40
0
-2
-1.5
-1
-0.5
00.5
1
1.5
2
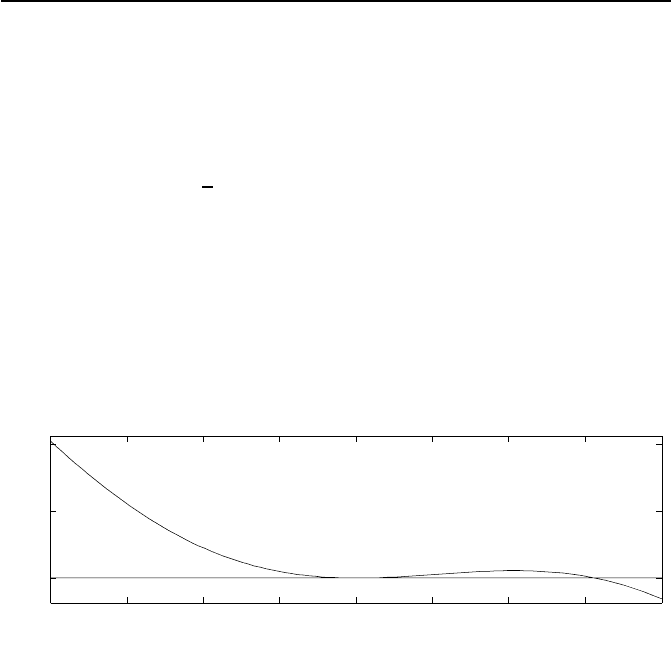
Bild 4.20: Verlauf der Control-Ljapunov-Funktion V (x)f
¨
ur den Fall x
2
=0sowie
δ
R
=60.41, a
1
=43.196 und a
3
=49.676.
Wir erhalten mit Gl. (4.54) und Gl. (4.55) f
¨
ur die Ableitung der Control-
Ljapunov-Funktion
˙
V (x)=−a
2
x
2
2
− u · a
3
x
2
sin(δ
R
+ x
1
). (4.56)
Wir w
¨
ahlen u in Gl. (4.56) zu
u = kx
2
· sin(δ
R
+ x
1
), (4.57)
so dass
˙
V (x)=−a
2
x
2
2
− a
3
kx
2
2
sin
2
(δ
R
+ x
1
) ≤ 0
ist. Es gilt nur
˙
V (x) ≤ 0, da
˙
V (x)=0f
¨
ur die Menge {x | x
1
∈ IR, x
2
=0}
gilt. Da aber von den interessierenden Zust
¨
anden nur der Punkt x = 0 aus
4.3. Control-Ljapunov-Funktionen 211
dieser Menge die Differenzialgleichung (4.54) erf
¨
ullt, ist
˙
V (x) entlang keiner
Trajektorie identisch null. Die Funktion V (x) ist also gem
¨
aß Definition 12
eine erweiterte Control-Ljapunov-Funktion und damit ist die Stabilit
¨
at der
Ruhelage x
R
= 0 gesichert. Der Wert k>0isteinfreiw
¨
ahlbarer Parameter.
In Originalkoordinaten hat das Regelgesetz (4.57) mit x
1
= δ − δ
R
und
x
2
=
˙
δ die Form
u = k
˙
δ sin(δ). (4.58)
Wir betrachten ein Beispiel mit P
T
= 540 MW, P
E
= 621 MVA, D =
4.6889 MW s, ω
e
=2π · 50 s
−1
, p = 1 und J = 39792 kg m
2
und erhalten so
a
1
=
P
T
Jω
e
=43.196,
a
2
=
D
Jω
e
=0.375,
a
3
=
P
E
Jω
e
=49.676.
Ein dreiphasiger Kurzschluss, der von t =4sbist =4.06 s andauert, wird als
Testfall betrachtet. In diesem Fall ist die
¨
ubertragene Leistung P = P
E
sin δ =
0f
¨
ur t ∈ [4, 4.06]. Als Reglerkonstante in Gl. (4.57) w
¨
ahlen wir den Wert
k =0.075.
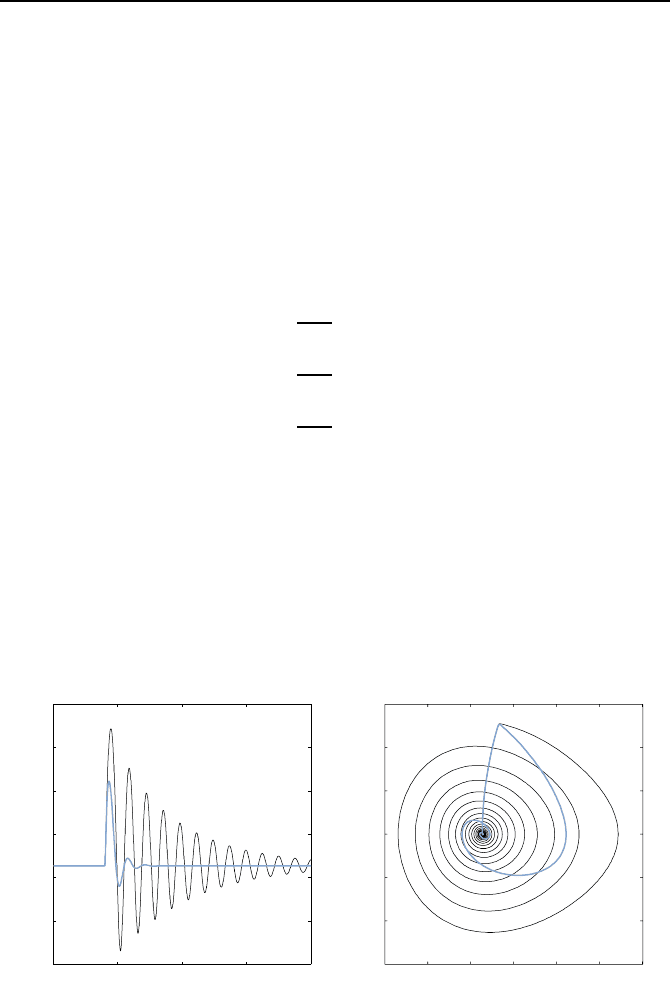
Bild 4.21 zeigt die Verl
¨
aufe des Winkels δ = x
1
+ δ
R
und die Trajektorien
[δ(t)
˙
δ(t)]
T
f
¨
ur das mit Gl. (4.57) geregelte System (4.54) bzw. das mit Gl.
(4.58) geregelte System (4.53) und das freie System. Man erkennt, dass sowohl
das freie als auch das geregelte System nach Ende des Kurzschlusses wieder
Zeit t in s
δ in rad
Polradwinkel δ in rad
˙
δ in rad s
−1
1.8
1.6
1.4
1.2
1
1
0.8
0.6
3
2
0
-1
-2
-3
0
5
10 15 20 0.6
0.8
11.21.4
1.6
1.8
Bild 4.21: Verl
¨
aufe des Polradwinkels δ = x
1
+ δ
R
im Fall des ungeregelten Systems
(schwarz) und des geregelten Systems (blau) und die entsprechenden Trajektorien-
verl
¨
aufe [δ(t)
˙
δ(t)]
T
.
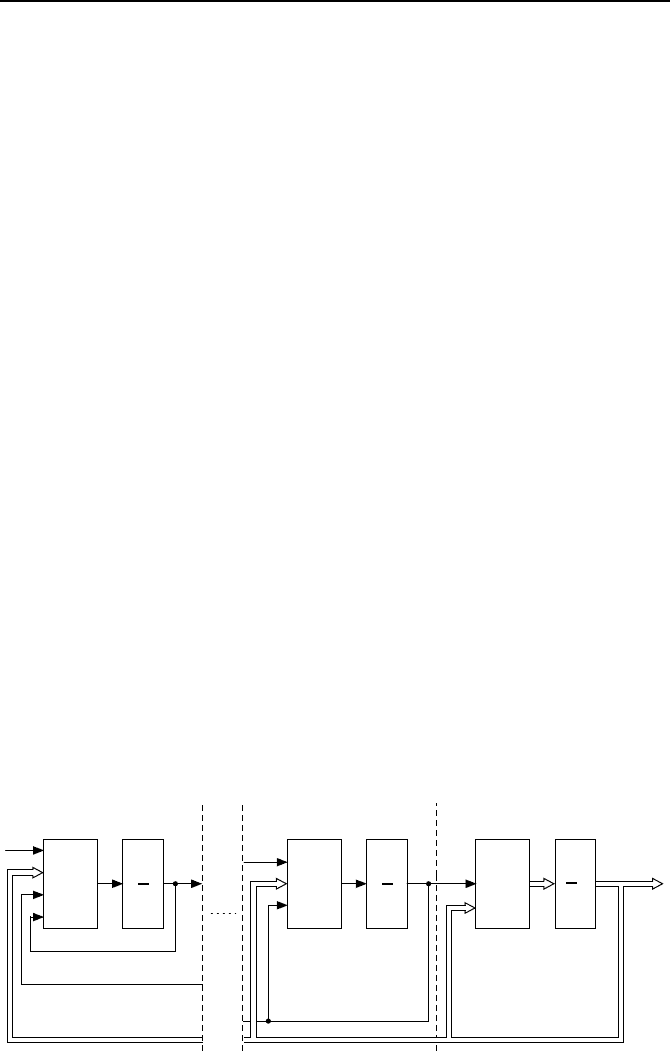
212 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
in die Ruhelage, d. h. den Betriebspunkt δ
R
=1.05 = 60.41
◦
,laufen.Durch
die Regelung wird erreicht, dass im Gegensatz zum freien System der Winkel
δ und somit die
¨
ubertragene Leistung P = P
E
sin(δ)kaumnochschwingt.
4.4 Das Backstepping-Verfahren
4.4.1 Idee des Verfahrens
Das Backstepping-Verfahren erm
¨
oglicht es, Regler und Ljapunov-Funktionen
f
¨
ur nichtlineare Regelstrecken vom Typ
˙x
1
= f
1
(x
1
)+h
1
(x
1
) · x
2
,
˙x
2
= f
2
(x
1
,x
2
)+h
2
(x
1
,x
2
) · x
3
,
˙x
3
= f
3
(x
1
,x
2
,x
3
)+h
3
(x
1
,x
2
,x
3
) · x
4
,
.
.
.
˙x
k
= f
k
(x
1
,x
2
,...,x
k
)+h
k
(x
1
,x
2
,...,x
k
) · u
zu bestimmen. Dabei gilt x
1
∈ IR
n
, x
2
,...,x
k
,u ∈ IR. Die Gestalt obiger
Systeme bezeichnet man als strenge R
¨
uckkopplungsform (engl. strict feedback
form). Sie bilden eine Unterklasse der eingangslinearen Systeme. Bild 4.22
illustriert die Systemstruktur der Regelstrecke.
Da man eingangslineare Systeme mittels der exakten Linearisierung sehr
gut regeln kann, stellt sich die Frage, warum ein weiteres Verfahren, wie das
Backstepping-Verfahren oder auch die Regelung mittels Control-Ljapunov-
Funktionen aus dem vorherigen Kapitel, n
¨
utzlich sein k
¨
onnte. Die Antwort
ist zum einen darin zu sehen, dass die exakte Linearisierung auf ein genau-
es Modell der Regelstrecke angewiesen ist. Zum anderen linearisiert dieses
Verfahren oft n
¨
utzliche Nichtlinearit
¨
aten der Regelstrecke mit unn
¨
otig hohem
Systemteil k
Systemteil 2 Systemteil 1
u
x
k
x
1
x
1
x
2
x
2
x
3
x
1
1
s
1
s
1
s
I
x
k−1
f
1
h
1
f
2
h
2
f
k
h
k
.
.
.
Bild 4.22: Struktur eines Systems in strenger R
¨
uckkopplungsform.

4.4. Das Backstepping-Verfahren 213
Stellaufwand. Das Backstepping-Verfahren wie auch die Control-Ljapunov-
Funktionen bieten hier M
¨
oglichkeiten, geeignete Nichtlinearit
¨
aten der Strecke
f
¨
ur die Regelung nutzbar zu machen und außerdem Robustheit der Regelung
gegen
¨
uber Ungenauigkeiten des Regelstreckenmodells zu erzielen [106].
Zur Bestimmung des Reglers u(x) und der Ljapunov-Funktion V (x)be-
trachtet man vorerst nur den Spezialfall
˙x
1
= f(x
1
)+h(x
1
) · x
2
, (4.59)
˙x
2
= u. (4.60)
Bild 4.23 zeigt die Struktur des Systems.
Die Zustandsgr
¨
oße x
2
wird nun als Eingangsgr
¨
oße des Systems (4.59) an-
gesehen. Es sei ein stetig differenzierbares Regelgesetz
x
2
= α(x
1
)mitα(0) = 0 (4.61)
bekannt, so dass x
1
= 0 eine asymptotisch stabile Ruhelage des mit α gere-
gelten Systems ist. Hierbei ist x
2
nat
¨
urlich nicht die reale Stellgr
¨
oße. Der Zu-
stand x
2
wird vielmehr zur Herleitung des eigentlichen Regelgesetzes u(x
1
,x
2
)
vor
¨
ubergehend als virtuelle Stellgr
¨
oße angesehen.
Des Weiteren soll eine Ljapunov-Funktion V (x
1
)f
¨
ur das mit dem virtuel-
len Regelgesetz (4.61) geregelte System (4.59) bekannt sein, d. h., es gilt
˙
V (x
1
)=
∂V
∂x
1
(f(x
1
)+h(x
1
) · α(x
1
)) < 0.
Um eine solche Ljapunov-Funktion V (x
1
) und einen Regler α(x
1
) zu finden,
kann man z. B. die Methodik der Control-Ljapunov-Funktionen aus dem vor-
herigen Abschnitt anwenden.
Das System (4.59), (4.60) wird nun in der Form
˙x
1
= f(x
1
)+h(x
1
) · α(x
1
)+h(x
1
)(x
2
− α(x
1
)), (4.62)
˙x
2
= u (4.63)
u
x
1
x
2
˙x
1
1
s
I
h(x
1
)
f (x
1
)
1
s
Bild 4.23: Struktur des Systems ˙x
1
= f (x
1
)+h(x
1
)x
2
mit ˙x
2
= u.
214 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
dargestellt. Das zugeh
¨
orige Strukturbild zeigt Bild 4.24. Man beachte, dass
die Systemdarstellungen (4.62) und (4.59)
¨
aquivalent sind.
Wir
¨
uberf
¨
uhren mittels der Transformation
z = x
2
− α(x
1
)
die Systemgleichungen (4.62) und (4.63) in die Form
˙x
1
= f(x
1
)+h(x
1
)α(x
1
)+h(x
1
) · z,
˙z = u − ˙α(x
1
),
(4.64)
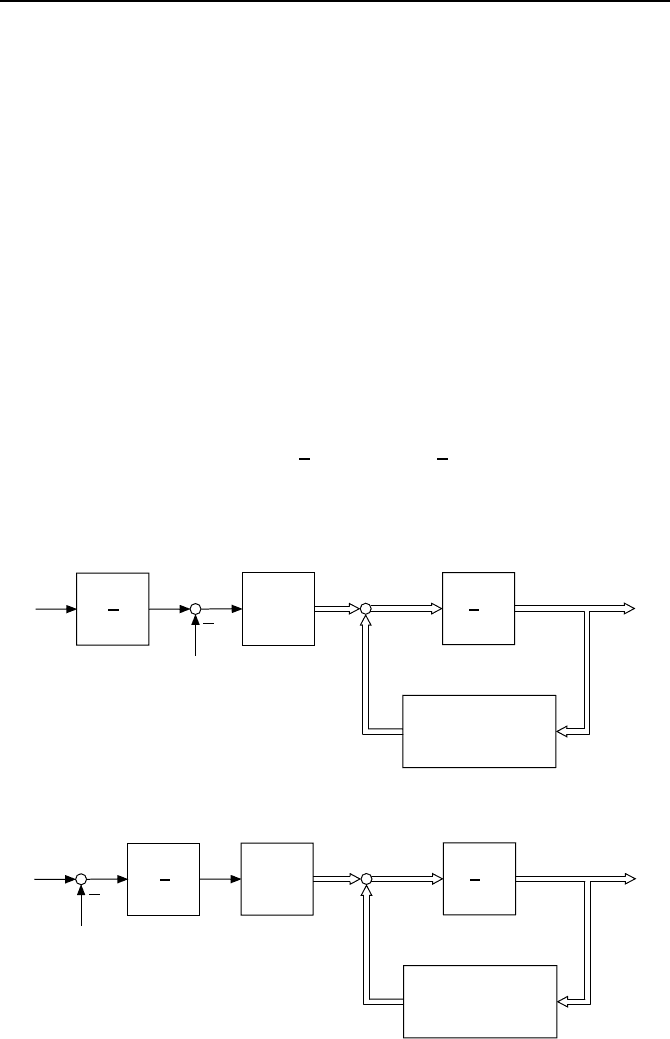
deren Struktur Bild 4.25 zeigt. Durch die Transformation wird das virtuelle
Regelgesetz α(x
1
) vor den Integrator geschoben, was der Methode den Namen
Backstepping bzw. Integrator-Backstepping gibt.
Wir setzen nun eine Ljapunov-Funktion f
¨
ur das Gesamtsystem (4.64) mit-
tels der als bekannt vorausgesetzten Ljapunov-Funktion V (x
1
) an und erhal-
ten
V
ges
(x
1
,x
2
)=V (x
1
)+
1
2
z
2
= V (x
1
)+
1
2
(x
2
− α(x
1
))
2
.
Es gilt mit Gl. (4.64) f
¨
ur die Ableitung der Ljapunov-Funktion
u
x
1
x
2
˙x
1
α(x
1
)
1
s
I
h(x
1
)
f(x
1
)+h(x
1
)α(x
1
)
1
s
Bild 4.24: System mit virtuellem Regelgesetz α(x
1
).
z
x
1
u
˙x
1
˙α(x
1
)
1
s
I
h(x
1
)
f(x
1
)+h(x
1
)α(x
1
)
1
s
Bild 4.25: Systemstruktur aus Bild 4.24 mit verschobenem Integrator.
4.4. Das Backstepping-Verfahren 215
˙
V
ges
(x
1
,x
2
)=
∂V
∂x
1
˙x
1
+z ˙z
=
∂V
∂x
1
(f(x
1
)+h(x
1
)α(x
1
))
< 0
+
∂V
∂x
1
h(x
1
)z+z (u − ˙α(x
1
)).
Man w
¨
ahlt
u − ˙α(x
1
)=−
∂V
∂x
1
h(x
1
) − k · z, k > 0, (4.65)
so dass f
¨
ur alle x
1
˙
V
ges
(x
1
,x
2
)=
∂V
∂x
1
(f(x
1
)+h(x
1
)α(x
1
)) − kz
2
< 0
gilt. Des Weiteren folgt mit
˙
x
1
= f(x
1
)+h(x
1
)x
2
aus Gl. (4.65)
u =˙α(x
1
) −
∂V
∂x
1
h(x
1
) − k · z
=
∂α
∂x
1
˙x
1
−
∂V
∂x
1
h(x
1
) − k (x
2
− α(x
1
))
=
∂α
∂x
1
(f(x
1
)+h(x
1
)x
2
) −
∂V
∂x
1
h(x
1
) − k (x
2
− α(x
1
)).
Hierbei ist k ein frei w
¨
ahlbarer positiver Parameter, mit dem die Dynamik des
Regelkreises beeinflusst werden kann. Große Werte k f
¨
uhren zu einer schnellen
Abnahme von V
ges
und somit meistens zu einer schnelleren Ausregelung.
Man hat also mit V
ges
eine Ljapunov-Funktion,
¨
ubrigens eine Control-
Ljapunov-Funktion, und mit obigem u ein Regelgesetz f
¨
ur die Regelstrecke
(4.59), (4.60) gefunden. Fasst man die obigen Ergebnisse zusammen, so ergibt
sich
Satz 23 (Einfaches Backstepping). Gegeben sei das System
˙x
1
= f(x
1
)+h(x
1
) · x
2
, (4.66)
˙x
2
= u. (4.67)
Es sei ein virtuelles Regelgesetz x
2
= α(x
1
) mit α(0)=0f
¨
ur das Teilsystem
(4.66) bekannt, das zu einer asymptotisch stabilen Ruhelage x
1R
= 0 des
Teilsystems (4.66) f
¨
uhrt. Ferner sei f
¨
ur das geregelte Teilsystem (4.66) eine
Ljapunov-Funktion V (x
1
) bekannt. Dann stabilisiert das Regelgesetz
u =
∂α(x
1
)
∂x
1
( f(x
1
)+h(x
1
) x
2
) −
∂V
∂x
1
h(x
1
) − k (x
2
− α(x
1
))
mit beliebigem k>0 die Ruhelage
x
T
1R
x
2R
T
= 0 asymptotisch und
V
ges
(x
1
,x
2
)=V (x
1
)+
1
2
(x
2
− α(x
1
))
2
ist eine Ljapunov-Funktion f
¨
ur das geregelte System.
