J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

226 Kapitel 4. Regelungen f

ur nichtlineare Regelstrecken

Somit erh

alt man f

ur das Regelgesetz mit

∂α

∂[x

]



(1 + p)β

+ β)



und

∂V

∂[x

]

=[x

]

die Gleichung

u = −x

+ k

− k

(1 + p)x

+ β

+ βx

−

p(1 + p)β(x

− x

)

+ β)

Mit k

= 1 gilt schließlich f

ur das Regelgesetz

u = βx

−

(1 + p)x

+ β

−

βp(1 + p)(x

− x

)

+ β)

Wir simulieren den ungeregelten Prozess und auch die Regelung f

ur p =10

und β = 6. Die Anfangswerte sind hierbei x

=5,x

= 5 und x

=5.Die

sich ergebenden Verl

aufe f

ur die Str

omungsgeschwindigkeit x

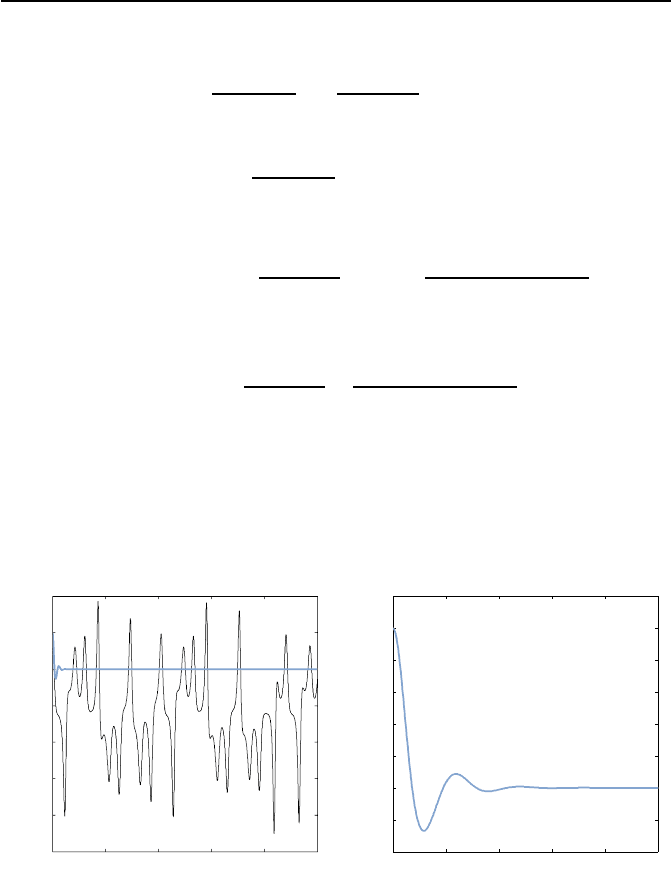
zeigt Bild 4.29.

Deutlich erkennbar ist, wie die Regelung das chaotische Verhalten unterdr

uckt

und der Prozess auf den station

aren Wert ausgeregelt wird.

-5

-10

-15

-20

-25

15 20 25

-1

-2

0.511.5

2.5

Zeit t in min

Bild 4.29: Verl

aufe der Abweichung x

der Str

omungsgeschwindigkeit von der Ruhe-

lage des ungeregelten chaotischen Prozesses (schwarz) und des geregelten Prozesses

(blau). Im rechten Teilbild ist der Ausregelverlauf in vergr

oßertem Maßstab noch-

mals dargestellt.

Nichtlineare Regelungen f

ur lineare und

nichtlineare Regelstrecken

5.1 Modellbasierte pr

adiktive Regelung

5.1.1 Grundlagen und Funktionsweise

Modellbasierte pr

adiktive Regelungen (MPR) sind die am h

auﬁgsten in der

Industrie eingesetzten fortgeschrittenen Regelungsverfahren [29, 78, 125, 155,

156]. In der Prozessindustrie, insbesondere in Raﬃnerien und der Chemie-

industrie, sind MPR etablierte Standardverfahren. MPR sind nichtlineare

Regelungsverfahren, die universell sowohl f

ur lineare Regelstrecken mit Be-

schr

ankungen von Stell- und Zustandsgr

oßen als auch f

ur nichtlineare Regel-

strecken geeignet sind.

Die Funktionsweise von MPR basiert dabei im Wesentlichen auf den Ei-

genschaften mathematischer Prozessmodelle. Diese haben in der Regelungs-

technik im Allgemeinen zwei Aufgaben. Zum einen soll ein Modell ein tieferes

Verst

andnis des Prozesses und seiner Funktionsweise erm

oglichen. Diese Ei-

genschaft wird zum Beispiel f

ur den Entwurf von Reglern genutzt. Zum an-

deren erlaubt ein Modell die Pr

adiktion zuk

unftigen Verhaltens. Genau diese

oglichkeit nutzen modellbasierte pr

adiktive Regelungen, indem sie online

anhand eines Prozessmodells den Ausgangsgr

oßenverlauf mittels des Stell-

oßenverlaufs optimieren. Der optimierte Stellgr

oßenverlauf wird dann zur

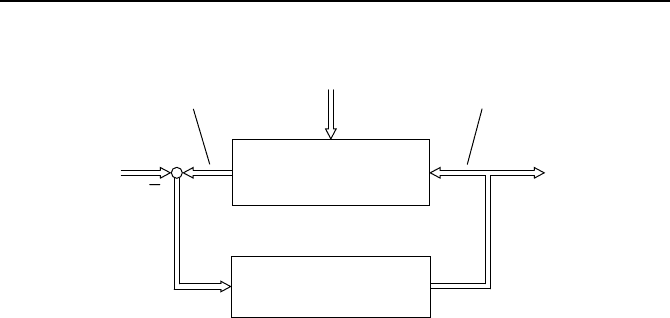
Regelung des eigentlichen Prozesses verwendet. Bild 5.1 illustriert den Vor-

gang.

Sowohl kontinuierliche wie auch diskrete Prozessmodelle k

onnen dabei zum

Einsatz kommen. In der Mehrzahl der F

alle werden allerdings diskrete oder

diskretisierte Modelle

x(k +1)=f (x(k), u(k)),

y(k)=g(x(k), u(k))

verwendet, denn im Fall kontinuierlicher Modelle gestaltet sich die Optimie-

rung des Stellgr

oßenverlaufes deutlich komplexer.

228 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

aktuelle

Zustandsgr

oßen des

Prozesses

adizierter

Ausgangsverlauf

Referenzverlauf

zur Regelstrecke

zuk

unftiger

Stellgr

oßenverlauf

Modell

Optimierer

Bild 5.1: Struktur eines modellbasierten pr

adiktiven Reglers.

Wir gehen aus vom Zeitpunkt k −1 mit bekannter Stellgr

oße u(k −1) und

beginnen ab diesem Zeitpunkt mit der Optimierung. Die Optimierung variiert

den zuk

unftigen Stellgr

oßenverlauf u(k + i) ab dem Zeitpunkt k f

ur eine end-

liche Zahl i =0,...,n

−1 von Stellgr

oßenschritten so, dass ein vorgegebenes

utemaß J minimal wird. Der Wert n

wird Stellhorizont genannt. H

auﬁg

verwendet wird das

uber n

Zeitschritte ermittelte quadratische G

utemaß

J =



i=1

||Q(y(k + i) − y

(k + i))||

+ r ·



i=1

||u(k + i − 1)||

(5.1)

mit der positiv deﬁniten Matrix Q, die oft eine Diagonalmatrix ist, oder

J =



i=1

||Q(y(k + i) − y

(k + i))||

+ r ·



i=1

||u(k + i − 1) − u(k + i − 2)||

(5.2)

Der Wert n

heißt Pr

adiktionshorizont,dadaszuk

unftige Verhalten

uber n

Zeitschritte vorausberechnet wird. In obigen G

utemaßen wird im ersten Sum-

menterm die Diﬀerenz zwischen der Ausgangsgr

oßenfolge y(k + i) und einem

Soll- oder Referenzverlauf y

(k+i) bewertet. Im zweiten Summenterm werden

die quadrierten Stellgr

oßen bzw. die Stellgr

oßendiﬀerenzen addiert und mit

dem Faktors r gewichtet. Bei der Minimierung von J sorgt dieser zweite Term

daf

ur, dass die Stellgr

oßen u(k + i) in Gl. (5.1) bzw. Stellgr

oßen

anderungen

in Gl. (5.2) keine zu großen Werte annehmen.

Die Pr

adiktion von y(k + i) erfolgt im G

utemaß J

uber n

Zeitschritte,

wobei n

≥ n

gilt. Der Pr

adiktionshorizont n

ist also gr

oßer als der Stellho-

rizont n

oder gleich groß. Damit auch f

ur den Zeitbereich i ≥ n

Stellgr

oßen

u(k + i) vorliegen, um y(k + i)pr

adizieren zu k

onnen, werden alle Stellgr

oßen

jenseits des Stellhorizontes auf u(k + n

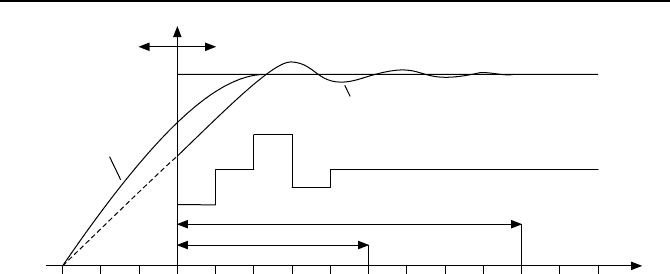
− 1) gesetzt. Bild 5.2 illustriert den

Ablauf.

5.1. Modellbasierte pr

adiktive Regelung 229

Zukunft

Vergangenheit

adiktion y(k + i)

y,u

Referenz

(k + i)

Stellhorizont n

adiktionshorizont n

u(k + i)

k + n

Zeitschritt

Bild 5.2: Prinzipieller Ablauf einer modellbasierten pr

adiktiven Regelung (MPR).

Nachdem die Optimierung die Stellgr

oßenfolge u

opt

(k + i)miti =0,...,

−1 ermittelt hat, wird nur der erste Wert dieser Folge, d. h. u

opt

(k)=u(k),

auf die reale Regelstrecke gegeben. Es wird also nicht die ganze Folge u(k + i)

ur die Regelung verwendet, sondern nur ihr erster Wert u(k). Sofort nach der

Aufschaltung von u(k) wird der oben beschriebene Pr

adiktions- und Optimie-

rungsprozess um einen Schritt in die Zukunft verschoben. Daher spricht man

auch von einem gleitenden Horizont. Der gleitende Horizont und die jeweils

nach einem Zeitschritt neu einsetzende Optimierung der Stellfolge u(k + i)

erlaubt eine Reaktion der MPR auf Prozessst

orungen.

Man kann die Funktionsweise der MPR mit der Vorgehensweise eines

Schachspielers vergleichen. Dieser spielt gedanklich verschiedene Zugfolgen

durch, wobei er drei, vier oder mehr Z

uge im Voraus betrachtet. Den ersten

der ihm optimal erscheinenden Kombination spielt er dann in der Realit

at.

Die nach jedem Zeitschritt neu einsetzende Pr

adiktion erfolgt, wie schon

beschrieben, auf Basis des Prozessmodells und der durch die Optimierung

errechneten Stellgr

oßenverl

aufe. Die Stellgr

oßenverl

aufe u(k+i) allein reichen

jedoch f

ur die Pr

adiktion nicht aus. Vielmehr muss auch der Zustand x(k)

zum Beginn des Pr

adiktionszeitraumes bekannt sein. Denn nur auf der Basis

des Zustandes x(k) – sozusagen dem Anfangszustand des Systems f

ur die

adiktion – und der Stellgr

oßenfolge u(k + i) kann die Ausgangsgr

oßenfolge

y(k + i) und damit das G

utemaß J berechnet werden. Im einfachsten Fall

bestimmt man x(k) durch Messung von x(k −1) und einem Rekursionsschritt

x(k)=f(x(k − 1), u(k − 1)). Ist die Messung nicht m

oglich, so muss x(k)

anhand der historischen Verl

aufe

u(k − 1), u(k − 2),...

und

y(k − 1), y(k − 2),...

durch einen Beobachter gesch

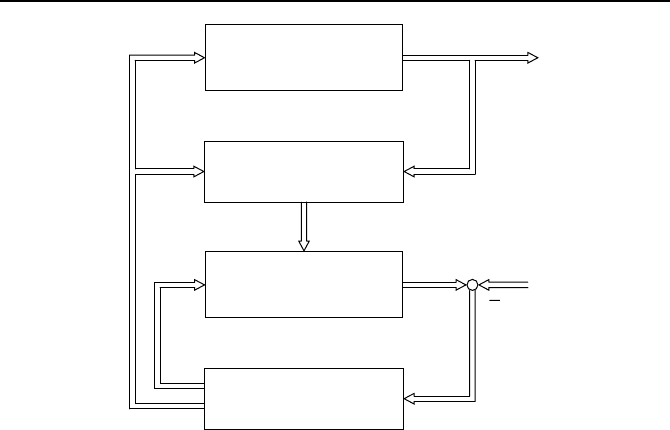
atzt werden. Fasst man alle Elemente einer MPR

zusammen, so ergibt sich der in Bild 5.3 gezeigte Aufbau.

230 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

˜x(k)

y(k)

(k+i)

y(k+i)

opt

(k)

opt

(k)

u(k+i)

Prozess

Beobachter

Modell

Optimierer

Bild 5.3: Struktur einer MPR mit Beobachter, Modell und Optimierer.

5.1.2 Lineare modellbasierte pr

adiktive Regelung

Die am h

auﬁgsten in der industriellen Praxis eingesetzten MPR basieren auf

linearen Prozessmodellen. Solche MPR bezeichnet man als lineare modellba-

sierte pr

adiktive Regelungen,abgek

urzt LMPR.

Verwendet man dabei das quadratische G

utemaß (5.1) oder (5.2), so ergibt

sich ein linearer Regler, wie wir im Folgenden sehen werden. Lineare Regler

onnen bekanntlich auch mit anderen, einfacheren Verfahren entworfen wer-

den. Der wahre Nutzen einer LMPR ergibt sich daher auch erst dann, wenn

man Nebenbedingungen in das Optimierungsproblem miteinbeziehen muss.

Dies k

onnen z. B. Stell-, Ausgangs- oder Zustandsgr

oßenbeschr

ankungen sein.

In diesem Fall ergibt sich ein nichtlinearer Regler. Die MPR wird allerdings

aufgrund des linearen Prozessmodells trotzdem als LMPR bezeichnet.

Wir betrachten den Fall einer linearen zeitdiskreten Regelstrecke

x(k +1)=Ax(k)+Bu(k),

y(k)=Cx(k)

(5.3)

mit x ∈ IR

, u ∈ IR

und y ∈ IR

.Vorerstber

ucksichtigen wir hierbei keine

Beschr

ankungen von u, x oder y d. h., wir betrachten nur den rein linearen

Fall. Sp

ater werden wir sehen, dass wir die hierbei erzielten Ergebnisse auch

ur den Fall mit Beschr

ankungen nutzen k

onnen. Die Betrachtung des rein

linearen Sonderfalls erm

oglicht uns im Besonderen einen einfachen Zugang

zum detaillierten Verst

andnis modellbasierter pr

adiktiver Regelungen.

5.1. Modellbasierte pr

adiktive Regelung 231

Der Stellgr

oßenvektor u(k) wird nun aus der vorherigen Stellgr

oße u(k−1)

und die im Schritt k stattﬁndende sprungf

ormige Ver

anderung Δu(k)gem

aß

u(k)=u(k − 1) + Δu(k) (5.4)

zusammengesetzt. Man erh

alt so f

ur die obige Systembeschreibung (5.3)

x(k +1)=Ax(k)+Bu(k − 1) + BΔu(k),

y(k)=Cx(k).

(5.5)

Wir betrachten im Weiteren alle Ausgangsvektoren y(k +i) beginnend mit

Schritt k + 1 bis zum Schritt k + n

,d.h.biszumPr

adiktionshorizont n

Wir erhalten aus Gl. (5.4) und Gl. (5.5) zuerst f

ur i ≤ n

die Beziehungen

y(k +1)=CAx(k)+CBu(k − 1) + CBΔu(k),

y(k +2)=CA

x(k)+C(A + I)Bu(k − 1) + C(A + I)BΔu(k)

+ CBΔu(k +1),

. (5.6)

y(k + i)=CA

x(k)+C



i−1

+ ...+ A + I



Bu(k − 1)



j=1



i−j

+ ...+ A + I



BΔu(k + j − 1),

y(k + n

)=CA

x(k)+C



−1

+ ...+ A + I



Bu(k − 1)



j=1



−j

+ ...+ A + I



BΔu(k + j − 1).

Obige Gleichungen beschreiben die Ausgangsgr

oßen bis zum Stellhorizont n

Hinter dem Stellhorizont i>n

andert sich die Stellgr

oße nicht mehr, d. h.

Δu(k + i − 1) = 0 f

ur i>n

. Dann gilt

y(k + n

+1)=CA

x(k)+C (A

+ ...+ A + I) Bu(k − 1)



j=1



+1−j

+ ...+ A + I



BΔu(k + j − 1),

. (5.7)

y(k + n

)=CA

x(k)+C



−1

+ ...+ A + I



Bu(k − 1)



j=1



−j

+ ...+ A + I



BΔu(k + j − 1).

Man fasst die Vektoren y(k +1) bisy(k + n

)imrn

× 1-Vektor

232 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

¯y(k +1)=

⎡

⎢

⎣

y(k +1)

y(k +2)

y(k + n

)

⎤

⎥

⎦

und die Stellgr

oßen

anderungen Δu(k)bisΔu(k +n

−1) im mn

×1-Vektor

Δ¯u(k)=

⎡

⎢

⎣

Δu(k)

Δu(k +1)

Δu(k + n

− 1)

⎤

⎥

⎦

zusammen. Man beachte, dass der Vektor Δ¯u(k) im Allgemeinen eine niedri-

gere Dimension als der Vektor ¯y(k + 1) besitzt, da n

≤ n

gilt.

ur die Gl. (5.6) und Gl. (5.7) erh

alt man zusammen

¯y(k +1)=Fx(k)+Gu(k − 1) + HΔ¯u(k), (5.8)

wobei

F =

⎡

⎢

⎣

⎤

⎥

⎦

, G=

⎡

⎢

⎣

C(A + I)B

C(A

+ A + I)B

C(A

−1

+ ...+ I)B

⎤

⎥

⎦

⎡

⎢

⎣

CB 0 ... 0

C(A + I)BCB··· 0

C(A

+ A + I)BC(A + I)B ··· 0

C(A

−1

+...+I)BC(A

−2

+...+I)B ··· CB

C(A

+...+I)BC(A

−1

+...+I)B ··· C(A + I)B

C(A

−1

+...+I)BC(A

−2

+...+I)B ··· C(A

−n

+...+I)B

⎤

⎥

⎦

mit F ∈ IR

×n

, G ∈ IR

×m

und H ∈ IR

×mn

gilt. Dabei ist der Anteil

g(k)=Fx(k)+Gu(k − 1)

in Gleichung (5.8) durch die schon erfolgten Schritte 0,...,k−1 der Regelung

vorgegeben. W

ahrend der Term g(k) also konstant ist, enth

alt der Anteil

HΔ¯u(k) in Gl. (5.8) die zu optimierende Stellgr

oßenfolge Δu(k),...,Δu(k +

− 1). Man verk

urzt Gl. (5.8) daher zu

5.1. Modellbasierte pr

adiktive Regelung 233

¯y(k +1)=g(k)+HΔ¯u(k). (5.9)

Minimiert werden soll nun das konvexe G

utemaß

J(Δ¯u(k)) = (¯y(k +1)− ¯y

(k +1))

Q (¯y(k +1)− ¯y

(k +1))

+ Δ¯u

(k)RΔ¯u(k),

(5.10)

wobei Q eine positiv deﬁnite rn

×rn

- Matrix und R eine positiv deﬁnite

×mn

-Matrixist.Derrn

- dimensionale Vektor

¯y

(k +1)=

⎡

⎢

⎣

(k +1)

(k +2)

(k + n

)

⎤

⎥

⎦

beinhaltet den Verlauf der Referenzgr

oße y

(k + i). Man setzt Gl. (5.9) in das

utemaß (5.10) ein und erh

alt mit der Abk

urzung

e(k)=g(k) − ¯y

(k +1)

die Darstellung

J(Δ¯u(k)) = (e(k)+HΔ¯u(k))

Q (e(k)+HΔ¯u(k)) + Δ¯u

(k)RΔ¯u(k)

= Δ¯u

(k)

QH + R

Δ¯u(k)

+2Δ¯u

(k)H

Qe(k)+e

(k)Qe(k). (5.11)

Die Bedingung f

ur ein Minimum dieser konvexen G

utefunktion,

∂J(Δ¯u(k))

∂Δ¯u(k)

= 0,

liefert die lineare Gleichung

QH + R

Δ¯u(k)+H

Qe(k)=0.

Hieraus ergeben sich die gesuchten Stellgr

oßen zu

Δ¯u(k)=−

QH + R

−1

Qe(k).

Von den im Vektor

Δ¯u(k)=

⎡

⎢

⎣

Δu(k)

Δu(k +1)

Δu(k + n

− 1)

⎤

⎥

⎦

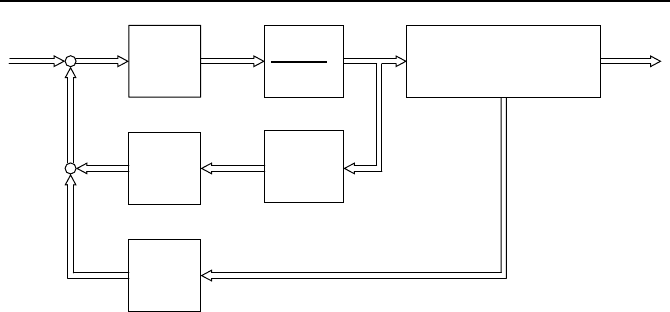
234 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

−K

1−z

−1

x(k+1)=Ax(k)+Bu(k)

y(k)=Cx(k)

−¯y

(k+1)

e(k)

Δu(k)

u(k)

y(k)

u(k−1)

x(k)

Bild 5.4: MPR f

ur eine lineare Regelstrecke ohne Beschr

ankungen.

zusammengefassten Stellgr

oßen wird allerdings, wie bereits erw

ahnt, nur der

erste Stellgr

oßenschritt Δu(k) zur Regelung genutzt. Wir betrachten daher

nur das erste Element

Δu(k)=−Ke(k)

dieses Vektors mit

K =



I 0 ···0





QH + R

−1



wobei I ∈ IR

m×m

ist. Das Regelgesetz ist linear, besitzt eine Dynamik und

lautet zusammengefasst

u(k)=u(k − 1) + Δu(k)=u(k − 1) − Ke(k),

e(k)=Fx(k)+Gu(k − 1) − ¯y

(k +1).

Bild 5.4 zeigt die zugeh

orige Struktur der linearen MPR ohne Beschr

an-

kungen. Auf einen Beobachter wurde dabei verzichtet. Ein solcher kann aber

ohne Weiteres zur Bestimmung des zur Regelung n

otigen Zustandsvektors

x(k) in den Regelkreis eingef

ugt werden.

5.1.3 LMPR mit Beschr

ankungen

Wie schon erw

ahnt, hat die lineare MPR ohne Beschr

ankungen keine große

praktische Relevanz und wurde hier vor allem beschrieben, um einen einfach

verst

andlichen Zugang zur Thematik zu ﬁnden und die prinzipielle Funktions-

weise zu erl

autern.

In der industriellen Praxis ﬁndet die lineare MPR Verwendung, wenn

die zu optimierenden Variablen beispielsweise im Stellgr

oßenvektor u(k)Be-

schr

ankungen

5.1. Modellbasierte pr

adiktive Regelung 235

⎡

⎢

⎣

min,1

min,2

min,m

⎤

⎥

⎦



 

min

≤

⎡

⎢

⎣

(k)

⎤

⎥

⎦



 

u(k)

≤

⎡

⎢

⎣

max,1

max,2

max,m

⎤

⎥

⎦



 

max

unterliegen. Diese Beschr

ankungen der Stellgr

oßen lassen sich auch in Abh

an-

gigkeit der Stellgr

oßen

anderungen darstellen. So schreibt man

min

≤ u(k)=u(k − 1) + Δu(k) ≤ u

max,

min

≤ u(k +1) =u(k − 1) + Δu(k)+ Δu(k +1) ≤ u

max,

min

≤ u(k +2) =u(k − 1) + Δu(k)+ Δu(k +1)+Δu(k +2)≤ u

max,

min

≤ u(k + n

− 1) =u(k − 1) +Δu(k)+ ... + Δu(k + n

− 1) ≤ u

max

(5.12)

Wir deﬁnieren ¯u

min



min

... u

min



und ¯u

max



max

... u

max



als

Vektoren der L

ange mn

. Gl. (5.12) l

asst sich dann in der Matrixform

¯u

min

≤ E · u(k − 1) + D · Δ¯u(k) ≤ ¯u

max

(5.13)

mit der mn

× m -Matrix

E =

⎡

⎢

⎣

⎤

⎥

⎦

und der unteren mn

× mn

- Dreiecksmatrix

D =

⎡

⎢

⎣

I 00··· 0

II0 ··· 0

III··· I

⎤

⎥

⎦

darstellen. Die Matrizen I sind Einheitsmatrizen der Dimension m × m.

Von Bedeutung sind des Weiteren Beschr

ankungen der

Anderungsrate der

Stellgr

oßen, d. h. Beschr

ankungen der Art

Δ¯u

min

≤ Δ

u(k) ≤ Δ¯u

max

. (5.14)

Die Vektoren Δ¯u

min

und Δ¯u

max

sind

ahnlich aufgebaut wie die Vektoren ¯u

min

und ¯u

max

und besitzen auch deren Dimension.

Außer Stellgr

oßen k

onnen auch Zustandsgr

oßen x

oder Ausgangsgr

oßen

Beschr

ankungen