J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.

256 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
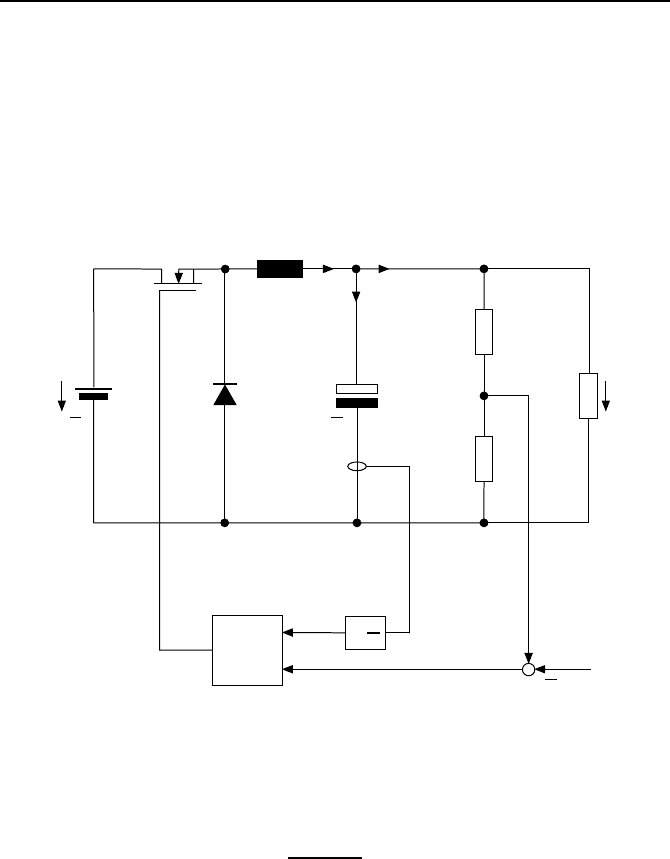
5.2.5 Beispiel DC-DC-Wandler
Ein DC-DC-Wandler, auch Gleichstromsteller oder getakteter Spannungsstel-
ler genannt, dient dazu, eine Gleichspannung in eine niedrigere bzw. h
¨
ohere
Spannung umzuwandeln. Dabei soll er m
¨
oglichst verlustarm arbeiten. Wir be-
trachten einen Abw
¨
artswandler [178], also einen Wandler, der eine Spannung
u
e
in eine niedrigere Spannung u
a
umwandelt. Bild 5.14 zeigt einen solchen
Wandler einschließlich des zugeh
¨
origen Reglers.
+
+
u
ref
u
a
u
e
x
1
x
2
βu
a
Regler
−
β
C
R
1
R
2
R
L
Strom-
messung
C
L
T
i
L
i
R
i
C
Bild 5.14: DC-DC-Wandler.
Aufgabe der Schaltung ist es, die Ausgangsspannung u
a
auf Basis einer
konstanten Referenzspannung u
ref
so einzustellen, dass
βu
a
=
R
2
R
1
+ R
2
u
a
= u
ref
(5.38)
gilt. Zu diesem Zweck wird ein Leistungs-MOSFET, im Bild 5.14 mit T ge-
kennzeichnet, als Schalter benutzt und
¨
uber den Regler ein- bzw. ausgeschal-
tet. Eine Schaltvariable z kennzeichnet den Schaltzustand des Transistors T .
Ist z = 1, so leitet der Transistor. Ist z = 0, so ist der Transistor gesperrt. Da-
bei wird eine Pulsweitenmodulation (PWM) durchgef
¨
uhrt. Diese bewirkt in
der Induktivit
¨
at L einen kontinuierlichen Stromfluss i
L
so, dass die Spannung
βu
a
¨
uber R
2
der Referenzspannung u
ref
entspricht, d. h., Gl. (5.38) erf
¨
ullt ist.
F
¨
ur die Ableitung ˙u
a
der Spannung
¨
uber dem Lastwiderstand R
L
bzw.
dem Gl
¨
attungskondensator C gilt

5.2. Strukturvariable Regelungen mit Gleitzustand 257
˙u
a
=
1
C
i
C
=
1
C
(i
L
− i
R
)=
1
C
u
e
z − u
a
L
dt −
u
a
R
G
. (5.39)
Dabei ist
R
G
=
(R
1
+ R
2
)R
L
R
1
+ R
2
+ R
L
.
Man erh
¨
alt aus Gl. (5.39)
¨u
a
= −
1
LC
u
a
−
1
R
G
C
˙u
a
+
u
e
z
LC
. (5.40)
Wir definieren als Zustandsvariablen
x
1
= βu
a
− u
ref
, (5.41)
x
2
=˙x
1
= β ˙u
a
.
Mit den Gl. (5.40) und (5.41) ergibt sich das Zustandsraummodell
˙x
1
˙x
2
=
⎡
⎣
01
−
1
LC
−
1
R
G
C
⎤
⎦
x
1
x
2
+
+
0
1
LC
,
u, (5.42)
wobei sich die Stellgr
¨
oße u aus
u = βu
e
z − u
ref
(5.43)
ergibt.
Das System (5.42), (5.43) ist ideal f
¨
ur die Anwendung einer Gleitzustands-
regelung. Denn zum einen ist durch die digitale Stellgr
¨
oße z schon ein Schalt-
vorgang vorgegeben. Zum anderen vertr
¨
agt der Leistungstransistor ein hoch-
frequentes Schalten, wie es bei Gleitzust
¨
anden auftritt. Ziel der Regelung ist
das Erreichen des Arbeitspunktes
x
1
= βu
a
− u
ref
=0, (5.44)
d. h. u
a
= u
ref
/β.
Das System (5.42) besitzt jeweils eine stabile Ruhelage x
R
f
¨
ur z = 1 und
z =0.ImFallz =1ist
x
R1
=
βu
e
− u
ref
0
,
was nach Gl. (5.41) einer Ausgangsspannung von u
a
= u
e
entspricht. Im Fall
z = 0 gilt
x
R2
=
−u
ref
0
,
woraus nach Gl. (5.41) eine Ausgangsspannung u
a
= 0 resultiert. Man be-
achte, dass der zu erreichende Arbeitspunkt (5.44) des Regelkreises nicht mit
einer der beiden Ruhelagen der Regelstrecke identisch ist.
258 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
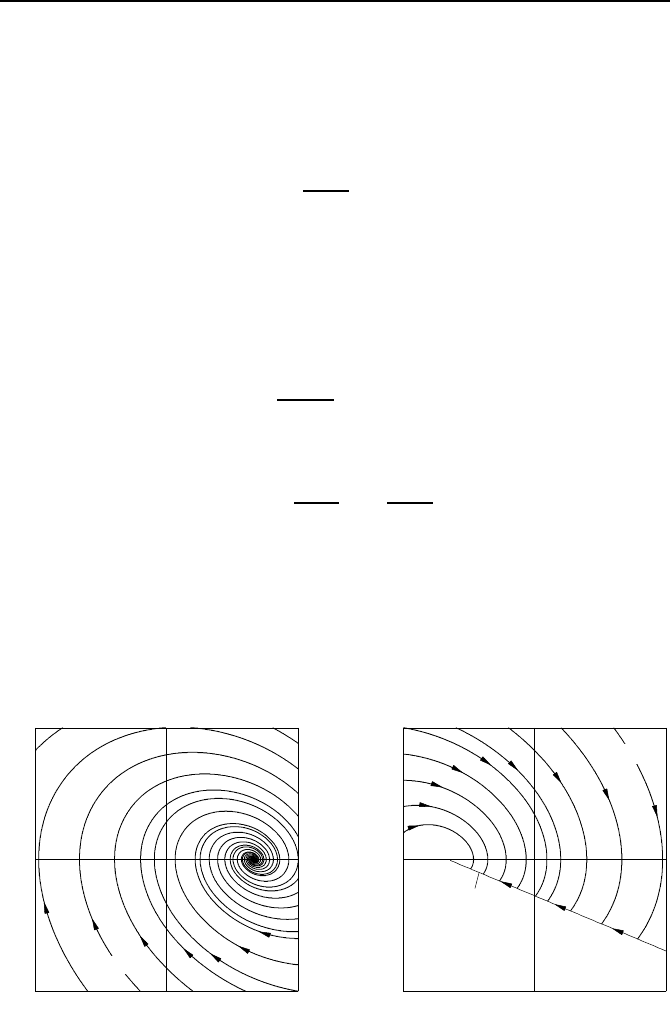
Wir wollen nun auch die Trajektorien x(t) des Wandlers betrachten. F
¨
ur
z = 1 ergeben sie sich aus Gl. (5.42) und sind in Bild 5.15 dargestellt. F
¨
ur
z = 0 ergeben sich die Trajektorien ebenfalls als L
¨
osungen von Gl. (5.42),
solange i
L
> 0 gilt. Ist die in der Spule gespeicherte Energie verbraucht, so
wird i
L
= 0. Dann sperrt die Diode und der Kondensator C entl
¨
adt sich
gem
¨
aß
˙u
a
+
1
R
G
C
u
a
=0,
woraus mit u
a0
= u
a
(0) die Beziehung
u
a
= u
a0
e
−t/(R
G
C)
folgt. F
¨
ur die Trajektorien x(t) gilt dann mit Gl. (5.41)
x
1
(t)=βu
a0
e
−t/(R
G
C)
− u
ref
, (5.45)
x
2
(t)=
−βu
a0
R
G
C
e
−t/(R
G
C)
(5.46)
und somit durch Einsetzen von Gl. (5.45) in Gl. (5.46)
x
2
= −
1
R
G
C
x
1
−
u
ref
R
G
C
. (5.47)
Im Fall z = 0 setzen sich die Trajektorien x(t) also aus zwei Teilst
¨
ucken
zusammen. Solange i
L
> 0 gilt, resultieren die Trajektorien aus den L
¨
osungen
von Gl. (5.42). Wird i
L
= 0, so laufen die Trajektorien auf die Gerade (5.47)
und auf ihr gem
¨
aß den Gl. (5.45) und (5.46) in die Ruhelage x
R2
. Bild 5.16
zeigt die Trajektorien hierzu.
Man w
¨
ahlt nun eine Schaltgerade
0
Zustand x
1
Zustand x
2
z =1
0
Bild 5.15: Ruhelage x
R1
und Trajek-
torien f
¨
ur den Fall z =1.
0
Zustand x
1
Zustand x
2
z =0
i
L
=0
0
Bild 5.16: Ruhelage x
R2
und Trajek-
torien f
¨
ur den Fall z =0.
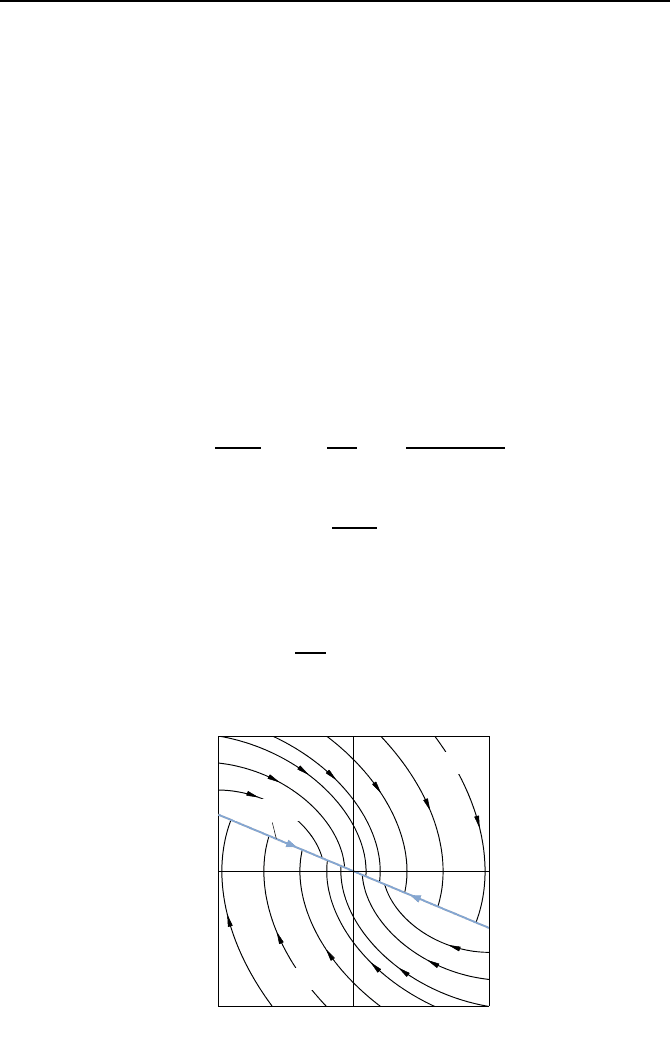
5.2. Strukturvariable Regelungen mit Gleitzustand 259
s(x)=r
1
x
1
+ x
2
= 0 (5.48)
mit r
1
> 0 und teilt so den Zustandsraum in zwei Bereiche. In einem Bereich
gilt z = 0, im anderen z =1,gem
¨
aß
z =
0f
¨
ur s(x) > 0,
1f
¨
ur s(x) < 0.
Bild 5.17 zeigt beide Bereiche und die jeweiligen Trajektorien. Bild 5.17 ist
dabei jeweils zur H
¨
alfte aus den Bildern 5.15 und 5.16 zusammengesetzt. An
der Schaltgeraden tritt ein Gleitzustand auf.
Wir wollen im Weiteren aus der notwendigen Bedingung f
¨
ur die Existenz
eines Gleitzustandes, s ˙s<0, den Parameter r
1
der Schaltgeraden (5.48) be-
stimmen. Aus
s ˙s = s(x) · grad
T
s(x) ·
˙
x < 0
und den Systemgleichungen (5.42) und (5.43) folgt
s ˙s = s(x)
r
1
−
1
R
G
C
x
2
−
1
LC
x
1
+
βu
e
z − u
ref
LC
< 0. (5.49)
Man w
¨
ahlt
r
1
=
1
R
G
C
,
denn dann ist die Existenzbedingung (5.49) unabh
¨
angig von x
2
= β ˙u
a
.Es
ergibt sich mit dieser Wahl von r
1
f
¨
ur Gl. (5.49) unter Nutzung der Gl. (5.41)
die Bedingung
s ˙s = s(x)
β
LC
(u
e
z − u
a
) < 0. (5.50)
0
Zustand x
1
Zustand x
2
z =0
z =1
s(x)=0
0
Bild 5.17: Trajektorien, Schaltgerade (blau) und Gleitzustand des DC-DC-Wandlers.

260 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
Aus dieser Bedingung erhalten wir im Fall s(x) < 0 und z =1
u
e
>u
a
. (5.51)
Im Fall s(x) > 0 und z =0erh
¨
alt man aus der Bedingung (5.50)
u
a
> 0. (5.52)
Da die Gl. (5.51) und (5.52) offensichtlich erf
¨
ullt sind, ist es die notwendi-
ge Bedingung (5.50) f
¨
ur die Existenz des Gleitzustandes ebenfalls. Weil des
Weiteren
˙s =
β
LC
(u
e
z − u
a
)
immer eine Abnahmerate von −u
a
β/LC < 0f
¨
ur s(x) > 0 und z = 0 bzw. eine
Zunahmerate von (u
e
−u
a
)β/LC > 0f
¨
ur s(x) < 0 und z = 1 aufweist, streben
die Trajektorien der Regelung auch in endlicher Zeit in den Gleitzustand.
Die Dynamik des geregelten Wandlers im Gleitzustand ergibt sich aus
s(x)=r
1
x
1
+ x
2
= 0 und x
2
=˙x
1
zu
x
1
(t)=x
1
(0)e
−r
1
t
, (5.53)
d. h., die Dynamik im Gleitzustand ist unabh
¨
angig von
¨
Anderungen des Last-
widerstandes R
L
oder Schwankungen der Eingangsspannung, d. h. der Batte-
riespannung u
e
.
Wir betrachten eine konkrete Ausf
¨
uhrung mit den Parametern u
e
=24V,
C = 100
F, L = 110 H, R
L
=6Ω,u
a
= 12 V und u
ref
=3.3V. Somit
ist β = u
ref
/u
a
=0.275. Aus R
2
= βR
1
/(1 − β) und R
1
= 870 Ω ergibt sich
R
2
= 330 Ω. Die Zeitkonstante 1/r
1
im Gleitzustand betr
¨
agt 0.6ms.
In Bild 5.18 ist der Verlauf einer Ausregelung f
¨
ur den Fall einer pl
¨
otzlichen
Abnahme der Eingangsspannung u
e
um 3 V dargestellt. Wie erwartet,
¨
andert
12.5
12
11.5
11
27
25
23
21
19
00.0025 0.005 0.0075 0.01
Zeit t in s
Ausgangsspannung u
a
in V
Eingangsspannung u
e
in V
Bild 5.18: Ausregelung der Ausgangs-
spannung u
a
nach einem Abfall der Ein-
gangsspannung u
e
.
14
12
10
8
6
4
2
0
0
0.0025 0.005 0.0075 0.01
Zeit t in s
Ausgangsspannung u
a
in V
Bild 5.19: Verlauf der Ausgangs-
spannung u
a
nach Einschalten des
Wandlers.
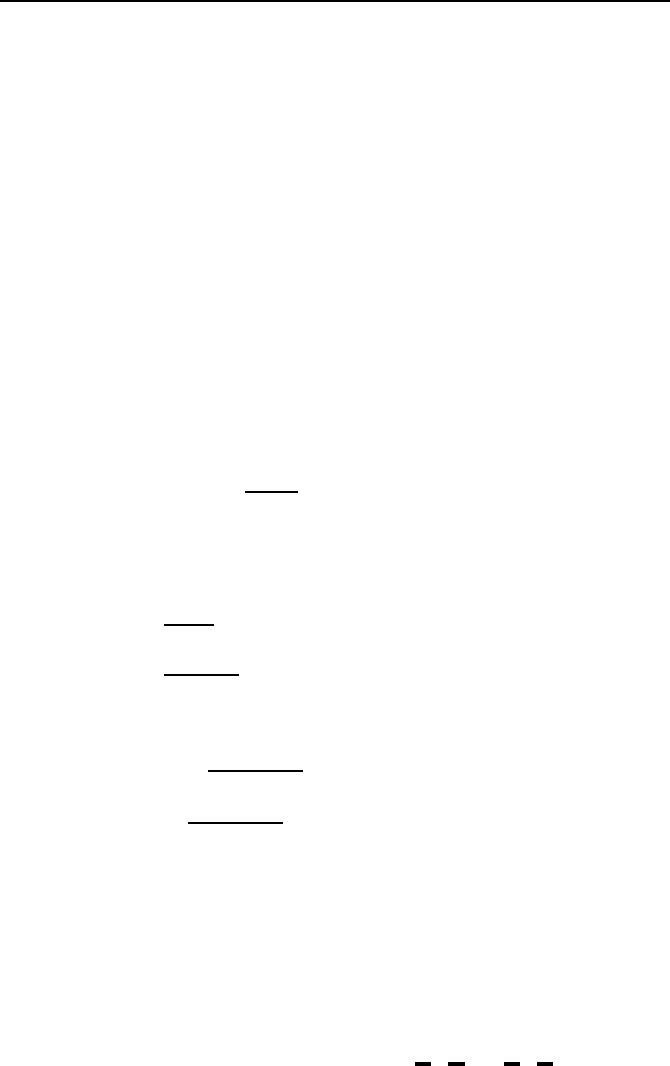
5.2. Strukturvariable Regelungen mit Gleitzustand 261
sich die Ausgangsspannung u
a
nicht. In realen Ger
¨
aten ist ein Spannungsabfall
von einigen 10 mV zu beobachten. Bild 5.19 zeigt den Einschaltverlauf. Der
Ausgangswert von u
a
= 12 V ist nach einer Zeit von ungef
¨
ahr 5/r
1
=3ms
erreicht.
5.2.6 Entwurf f
¨
ur nichtlineare Regelstrecken
Der Entwurf von Gleitzustandsreglern f
¨
ur nichtlineare Regelstrecken ist in
bestimmten F
¨
allen nicht schwieriger als der f
¨
ur lineare Regelstrecken. Dies
gilt beispielsweise f
¨
ur eingangslineare Regelstrecken
˙x = a(x)+b(x) · u,
y = c(x)
(5.54)
mit einem relativen Grad von δ = n. F
¨
ur δ<nist der Entwurf
¨
ahnlich.
Die obige Systemdarstellung
¨
uberf
¨
uhren wir, wie in Abschnitt 4.2.1 im
Fall des Reglerentwurfes mittels exakter Linearisierung, in die nichtlineare
Regelungsnormalform. Zu diesem Zweck verwenden wir die Lie-Derivierte
L
f
h(x)=
∂h(x)
∂x
f(x) = grad
T
h(x) · f(x).
Wir berechnen
y = c(x),
˙y =
∂c(x)
∂x
˙x = L
a
c(x),
¨y =
∂L
a
c(x)
∂x
˙x = L
2
a
c(x),
.
.
.
y
(n−1)
=
∂L
n−2
a
c(x)
∂x
˙x = L
n−1
a
c(x),
y
(n)
=
∂L
n−1
a
c(x)
∂x
˙x = L
n
a
c(x)+L
b
L
n−1
a
c(x) · u
und erhalten mit den neuen Zustandskoordinaten z
1
= y, z
2
=˙y, ..., z
n
=
y
(n−1)
und der daraus folgenden Transformation z = t(x) die Darstellung des
Systems (5.54) in nichtlinearer Regelungsnormalform
⎡
⎢
⎢
⎢
⎣
˙z
1
.
.
.
˙z
n−1
˙z
n
⎤
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎣
z
2
.
.
.
z
n
L
n
a
c(x)+L
b
L
n−1
a
c(x) · u
⎤
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎣
z
2
.
.
.
z
n
α(z)
⎤
⎥
⎥
⎥
⎦
˜a(z)
+
⎡
⎢
⎢
⎢
⎣
0
.
.
.
0
β(z)
⎤
⎥
⎥
⎥
⎦
˜
b(z)
u (5.55)

262 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
mit α(z)=L
n
a
c(t
−1
(z)) und β(z)=L
b
L
n−1
a
c(t
−1
(z)).
Der Entwurf eines Gleitzustandsreglers mit der Schaltfl
¨
ache s(z)=0ge-
schieht
¨
ahnlich wie im linearen Fall. Wir verwenden wieder den Ansatz
˙s(z)=−q sgn(s(z)) − ks(z) (5.56)
von Gao und Hung. Dieser, wir erinnern uns, stellt sicher, dass die Trajektorien
z(t) die Schaltfl
¨
ache in endlicher Zeit erreichen. Es gilt q>0 und k>0.
Unter Verwendung von ˙s(z) = grad
T
s(z)· ˙z und Gl. (5.55) sowie Gl. (5.56)
ergibt sich f
¨
ur das Regelgesetz
u(z)=−
grad
T
s(z) · ˜a(z)+q sgn(s(z)) + ks(z)
grad
T
s(z) ·
˜
b(z)
.
F
¨
ur den Fall einer Schalthyperebene s(z)=r
T
z = 0 vereinfacht es sich zu
u(z)=−
r
T
˜a(z)+q sgn(r
T
z)+k r
T
z
r
T
˜
b(z)
. (5.57)
Setzen wir nun r
T
=[r
1
r
2
··· r
n−1
1], so gilt f
¨
ur Gl. (5.57)
u(z)=−
r
1
z
2
+ ...+ r
n−1
z
n
+ k r
T
z + α(z)+q sgn(r
T
z)
β(z)
. (5.58)
Eingesetzt in die Regelstrecke (5.55) ergibt sich so f
¨
ur den Regelkreis
⎡
⎢
⎢
⎢
⎣
˙z
1
.
.
.
˙z
n−1
˙z
n
⎤
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎣
z
2
.
.
.
z
n
−kr
1
z
1
− (r
1
+ kr
2
)z
2
− ...− (r
n−1
+ k)z
n
⎤
⎥
⎥
⎥
⎦
−
⎡
⎢
⎢
⎢
⎣
0
.
.
.
0
q sgn(r
T
z)
⎤
⎥
⎥
⎥
⎦
.
Dieser Regelkreis ist frei von Nichtlinearit
¨
aten der Regelstrecke. Weiterf
¨
uhren-
des, z. B. f
¨
ur nichtlineare MIMO-Systeme, findet sich in [33, 58, 145, 170].
5.2.7 Beispiel optischer Schalter
Wir entwerfen im Weiteren einen Gleitzustandsregler f
¨
ur einen optischen
Schalter. Dieser ist als mikro-elektro-mechanisches System, abgek
¨
urzt MEMS,
ausgelegt und dient dazu, die Lichtbahn zwischen verschiedenen Lichtwellen-
leitern umzuschalten [24, 141]. So ist es m
¨
oglich, ein optisches Signal ohne
Wandlung in ein elektrisches und wieder zur
¨
uck von einem Lichtwellenleiter
in einen anderen zu leiten.
Das Bild 5.20 zeigt den Aufbau eines solchen optischen Schalters. Der
Kammantrieb wandelt eine elektrische Spannung v, die das Eingangssignal
des Schalters bildet, in eine translatorische Ver
¨
anderung der Position x
1
eines
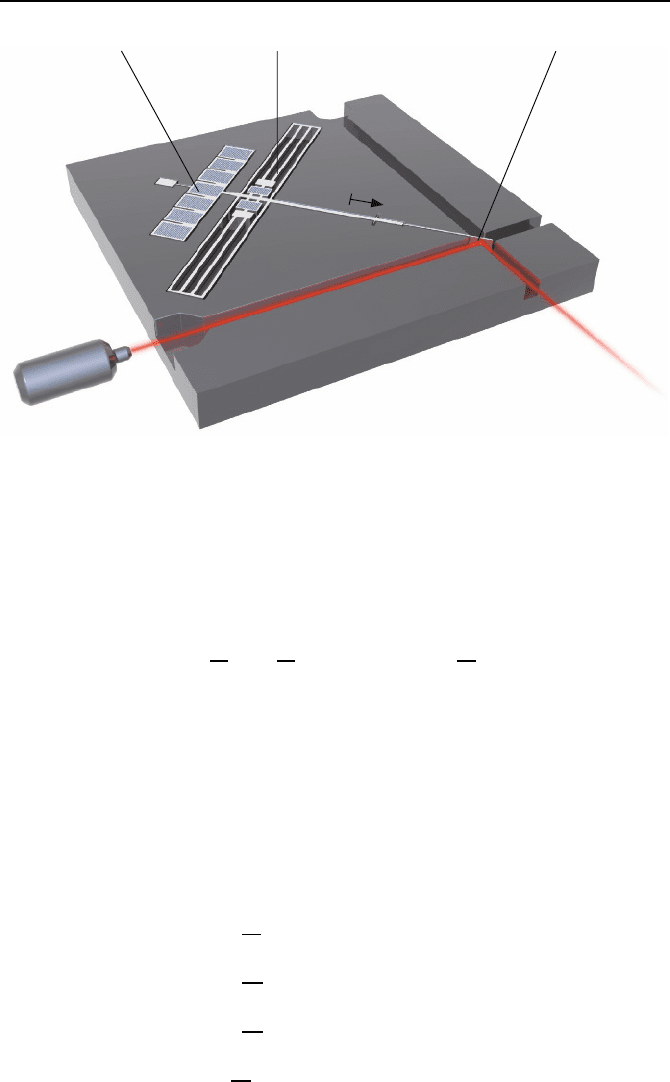
5.2. Strukturvariable Regelungen mit Gleitzustand 263
Laser
Kammantrieb
D
¨
ampfung Spiegel
x
1
Bild 5.20: Optischer Schalter in mikro-elektro-mechanischer Ausf
¨
uhrung.
Stabes um. An dem Stab ist ein Spiegel befestigt, der auf diese Weise in den
optischen Pfad hinein- und herausgeschoben werden kann. Das Modell des
optischen Schalters ist in nichtlinearer Regelungsnormalform
˙x
1
= x
2
,
˙x
2
= −
κ
m
x
1
−
1
m
(d
1
x
1
+ d
0
) · x
2
+
k
e
m
u + d
(5.59)
gegeben. Dabei ist u = v
2
,f
¨
ur die Ausgangsgr
¨
oße des Systems gilt y = x
1
und d ist eine z. B. mechanisch einwirkende, zeitabh
¨
angige St
¨
orung. Die zur
Verf
¨
ugung stehende Spannung v ist beschr
¨
ankt. Es gilt 0 ≤ v ≤ 35 V.
Die Parameter sind die bewegte Masse m =2.35 · 10
−9
kg, die Stei-
figkeit der Aufh
¨
angung, κ =0.6Nm
−1
,dieD
¨
ampfungskoeffizienten d
1
=
0.0363 kg s
−1
m
−1
und d
0
=5.45 · 10
−7
kg s
−1
sowie die Wandlerkonstan-
te k
e
=17.8 · 10
−9
NV
−2
des Kammantriebes. Die D
¨
ampfungskoeffizienten
d
0
und d
1
m
¨
ussen hierbei als unsichere Sch
¨
atzung angesehen werden. Der
¨
Ubersichtlichkeit halber k
¨
urzen wir
a
0
=
κ
m
=2.55 · 10
8
Nm
−1
kg
−1
,
a
1
=
d
1
m
=1.54 · 10
7
s
−1
m
−1
,
a
2
=
d
0
m
= 232 s
−1
,
b =
k
e
m
=7.57 N kg
−1
V
−2

264 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
ab.
Wir wollen verschiedene Positionen x
1R
des Spiegels vorgeben k
¨
onnen.
Diese Sollpositionen x
1R
korrespondieren mit den Ruhelagen
x
R
=
⎡
⎣
b
a
0
u
R
0
⎤
⎦
, (5.60)
wobei u
R
die Stellgr
¨
oße ist, die im Falle der Ruhelage x
R
ben
¨
otigt wird. Wir
erhalten so unter Verwendung von Gl. (5.60) und
x
1
= x
1R
+ Δx
1
=
b
a
0
u
R
+ Δx
1
f
¨
ur das Modell (5.59) die Darstellung
Δ ˙x
1
= x
2
,
˙x
2
= −(a
0
+ a
1
x
2
)(x
1R
+ Δx
1
) − a
2
x
2
+ bu+ d.
(5.61)
Als Schaltgerade betrachten wir
s(x)=r · Δx
1
+ x
2
=0
mit einem noch zu bestimmenden Parameter r. Mit dem Ansatz von Gao und
Hung aus Gl. (5.56) gilt
˙s(x)=−q sgn(s(x)) − ks(x).
Hieraus folgt durch Gleichsetzen mit ˙s(x) = grad
T
s(x) · (a(x)+b(x)u)das
Regelgesetz, das wir schon in Gl. (5.58) allgemein hergeleitet hatten, zu
u(x)=−
rx
2
−(a
0
+ a
1
x
2
)(x
1R
+ Δx
1
)−a
2
x
2
+q sgn(s(x))+ks(x)
b
. (5.62)
Dabei sind q und k noch zu w
¨
ahlende Konstanten. Setzt man das Regelgesetz
(5.62) in die Systemdynamik (5.61) ein, so ergibt sich f
¨
ur den Regelkreis
Δ ˙x
1
= x
2
,
˙x
2
= −rx
2
− q sgn(s(x)) − ks(x)+d
bzw. nach Einsetzen von s(x)=rΔx
1
+ x
2
Δ ˙x
1
= x
2
,
˙x
2
= −krΔx
1
− (r + k)x
2
− q sgn(rΔx
1
+ x
2
)+d.
(5.63)
Dieser Regelkreis besitzt, wenn man den nichtlinearen Teil einmal aus-
blendet, d. h. q = 0 gilt, eine lineare Dynamik mit dem charakteristischen
Polynom
5.2. Strukturvariable Regelungen mit Gleitzustand 265
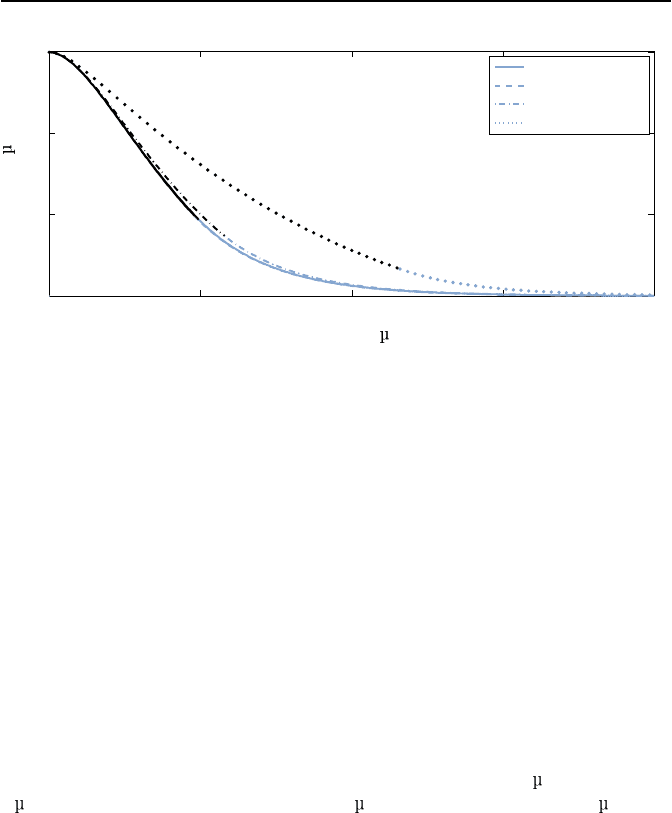
15
10
5
0
0
100 200 300 400
d
1
= d
nom
d
1
=0
d
1
=10d
nom
d
1
= 100 d
nom
Zeit t in s
Δx
1
in m
Bild 5.21: Ausregelung der Ausgangsspannung u
a
nach einem Abfall der Eingangs-
spannung u
e
f
¨
ur verschiedene D
¨
ampfungswerte d
1
. Bei blauen Kurventeilen ist das
System im Gleitzustand, bei schwarzen nicht.
P (λ)=λ
2
+(r + k)λ + rk.
Das Polynom hat die Nullstellen λ
1
= −r und λ
2
= −k,diemitdenEigen-
werten der linearen Systemdynamik des Modells (5.63) identisch sind.
Wir simulieren den Regelkreis (5.63) f
¨
ur die Parameter k = 20000, r =
20000 und q = 1000 f
¨
ur verschiedene D
¨
ampfungswerte
d
1
= d
nom
=0.0363,
d
1
=0,
d
1
=10d
nom
,
d
1
= 100d
nom
.
Dabei betrachten wir eine Anfangsauslenkung von x
1
(0) = 25 m und x
2
(0) =
0
ms
−1
. Die Ruhelage x
R1
liegt bei 10 m. Somit ist Δx
1
(0) = 15 m. F
¨
ur
die St
¨
orung gilt hier d = 0. Bild 5.21 zeigt die Ausregelverl
¨
aufe f
¨
ur die vier
verschiedenen D
¨
ampfungswerte. Man erkennt das in allen vier F
¨
allen gute
Regelverhalten. Bei blau gezeichneten Verl
¨
aufen befindet sich der Regelkreis
im Gleitzustand, bei schwarz gezeichneten Verl
¨
aufen bewegt sich das System
noch auf die Schaltgerade zu. Bei den Werten d
1
= d
nom
und d
1
= 0 sind die
Verl
¨
aufe nahezu identisch.
Angemerkt sei auch, dass eine Gleitzustandsregelung immer nur dann ro-
bust ist, wenn sie sich im Gleitzustand befindet. Ver
¨
andert sich die Regelstre-
cke so, dass der Gleitzustand nicht mehr existiert oder nicht mehr erreicht
wird, so ist der Regelkreis auch nicht mehr robust im beschriebenen Sinne.
F
¨
ur den obigen Regelkreis reduziert sich die Robustheit erst f
¨
ur sehr große
Werte d
1
d
nom
.
