J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.

6
Beobachter f
¨
ur nichtlineare Systeme
6.1 Beobachtbarkeit nichtlinearer Systeme
6.1.1 Definition der Beobachtbarkeit
Im Fall nichtlinearer Regelkreise mit Zustandsregler stellt sich die Frage, wie
man die Zustandsgr
¨
oßen x
i
der Regelstrecke ermittelt, wenn man sie nicht
messen kann oder will. Die Situation ist also vergleichbar mit dem Fall linearer
Systeme in Zustandsraumdarstellung, bei denen auch oft die Zustandsgr
¨
oßen
x
i
nicht messbar sind oder die Messung zu kostenintensiv ist.
Im linearen Fall setzt man zur L
¨
osung dieses Problems Beobachter ein,
mittels derer die Zustandsgr
¨
oßen x
i
gesch
¨
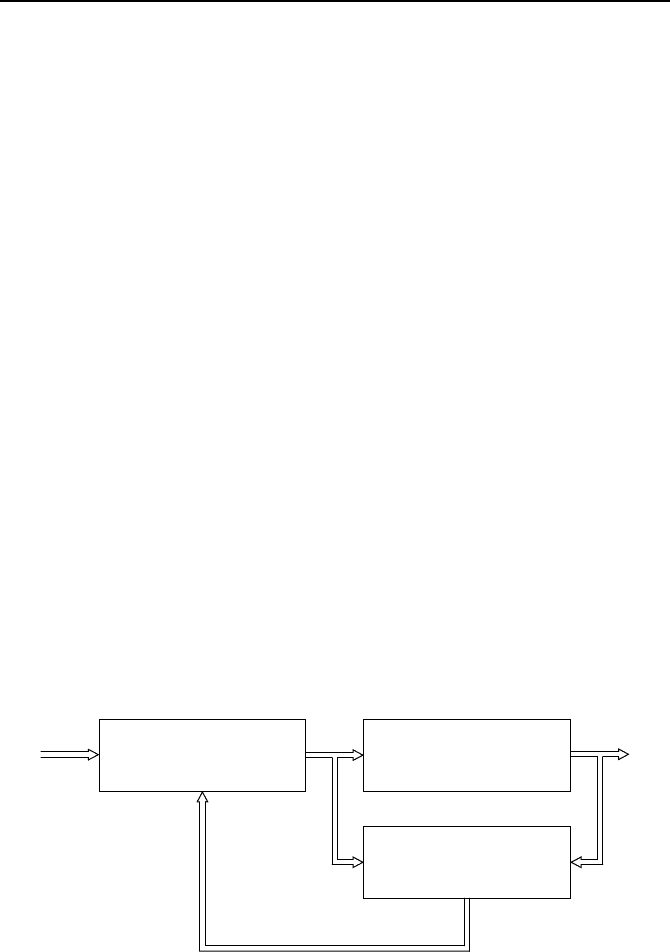
atzt werden. Bild 6.1 zeigt einen
solchen Zustandsregelkreis mit Beobachter. Insbesondere gilt im linearen Fall
das Separationstheorem, d. h., man kann die Dynamik des Beobachters und
die des Regelkreises unabh
¨
angig voneinander
¨
uber die Beobachtermatrix L
und die Reglermatrix K festlegen.
Beobachter sind auch im Fall nichtlinearer Systeme einsetzbar. Allerdings
ist dies nicht so einfach wie im linearen Fall m
¨
oglich. Die Stabilit
¨
at von nicht-
linearen Regelungssystemen mit Beobachter ist n
¨
amlich oft nicht oder nur
w
u
˜
x
y
u =w −K ˜x
˙x = Ax+ Bu
y = Cx
˙
˜x =(A − LC) ˜x
+Bu+ Ly
Bild 6.1: Linearer Zustandsregelkreis mit Beobachter.
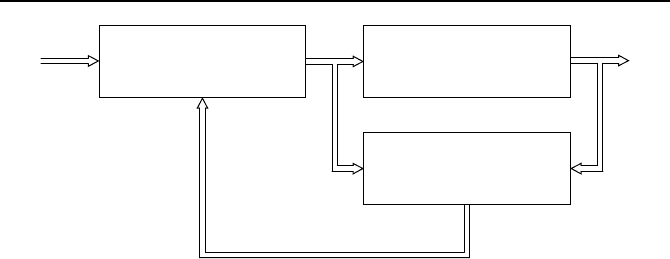
288 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
w
u
˜
x
y
u =K(w, ˜x)
˙x = f (x, u)
y = g(x, u)
Beobachter
Bild 6.2: Nichtlinearer Zustandsregelkreis mit Beobachter.
schwer nachweisbar. Und im Allgemeinen gilt das Separationstheorem nicht.
Die prinzipielle Struktur eines solchen Regelkreises mit Beobachter zeigt Bild
6.2.
Welcher Natur der nichtlineare Beobachter im speziellen Fall ist, h
¨
angt
vom Charakter der Regelstrecke ab. Die nachfolgenden Kapitel beschreiben
einige der g
¨
angigen Typen. Erg
¨
anzende Literatur bieten [17, 20, 42, 43, 70, 93].
Bevor aber ein Beobachter entworfen werden kann, muss sichergestellt werden,
dass das nichtlineare System auch wirklich beobachtbar ist [20, 59, 70, 195].
(In der Praxis wird dieser Schritt auch schon mal vernachl
¨
assigt.) Zu diesem
Zweck muss der Begriff der Beobachtbarkeit zuerst einmal definiert werden.
Dabei muss zwischen globaler und lokaler Beobachtbarkeit unterschieden wer-
den.
Definition 15 (Globale Beobachtbarkeit). Ein System
˙x = f(x, u) mit x(t
0
)=x
0
,
y = g(x, u)
sei f
¨
ur x ∈ D
x
⊆ IR
n
und u ∈ C
u
⊆ C
n−1
definiert und es sei y ∈ IR
r
.
Sind dann alle Anfangsvektoren x
0
∈ D
x
aus der Kenntnis von u(t) und y(t)
in einem Zeitintervall [t
0
,t
1
< ∞] f
¨
ur alle u ∈ C
u
eindeutig bestimmbar, so
heißt das System global beobachtbar.
Dabei ist C
n−1
der Raum der (n − 1) - mal stetig differenzierbaren Vek-
torfunktionen, hier der Funktion u(t).
¨
Ahnlich, aber schw
¨
acher in der Anfor-
derung an das System, definieren wir den Begriff der lokalen Beobachtbarkeit.
Definition 16 (Lokale Beobachtbarkeit). Ein System
˙x = f(x, u) mit x(t
0
)=x
0
,
y = g(x, u)
sei f
¨
ur x ∈ D
x
⊆ IR
n
und u ∈ C
u
⊆ C
n−1
definiert und es sei y ∈ IR
r
.Sind
dann alle Anfangsvektoren x
0
∈ D
x
in einer Umgebung
6.1. Beobachtbarkeit nichtlinearer Systeme 289
U = {x
0
∈ IR
n
|||x
0
− x
p
|| <ρ}
eines Punktes x
p
∈ D
x
aus der Kenntnis von u(t) und y(t) in einem Zeitin-
tervall [t
0
,t
1
< ∞] f
¨
ur alle u ∈ C
u
eindeutig bestimmbar, so heißt das System
lokal beobachtbar, wenn dies f
¨
ur alle x
p
∈ D
x
m
¨
oglich ist.
In vielen F
¨
allen sind lokal beobachtbare Systeme auch global beobachtbar.
Bei linearen Systemen ist dies immer so. Als ein Beispiel, das lokal beobachtbar
ist, aber nicht global, betrachten wir das nichtlineare autonome System
˙x = −x +
−1,x<0,
1,x>0,
(6.1)
y = x
2
.
Der Definitionsbereich von x ist D
x
= IR\{0}.
Offensichtlich kann man aus der Kenntnis von y(t) nicht eindeutig den
Anfangswert x
0
bestimmen, denn die Ausgangsgleichung y = x
2
besitzt die
zwei L
¨
osungen
x
1
= −
√
y und x
2
=
√
y.
Daher ist das System (6.1) nicht global beobachtbar. Es ist aber lokal be-
obachtbar. Denn f
¨
ur alle Werte x aus einer geeignet gew
¨
ahlten Umgebung
U = {x
0
∈ IR ||x
0
− x
p
| <ρ} eines jeden Punktes x
p
∈ D
x
ist aus y = x
2
eindeutig der Wert x,alsox
0
, bestimmbar. D. h., es gilt
x
0
= −
y(t
0
)f
¨
ur x
p
< 0,ρ<|x
p
|,
und
x
0
=
y(t
0
)f
¨
ur x
p
> 0,ρ<|x
p
|.
Bei nichtlinearen Systemen ist gem
¨
aß den obigen Definitionen zwischen
globaler und lokaler Beobachtbarkeit zu unterscheiden. Lineare Systeme da-
gegen sind, wie gesagt, wenn sie lokal beobachtbar sind, auch immer global
beobachtbar und nat
¨
urlich umgekehrt. Bei nichtlinearen Systemen kann es
des Weiteren vorkommen, dass ihre Beobachtbarkeit vom Eingangsvektor u
abh
¨
angt. Die Beobachtbarkeit eines linearen Systems ist dagegen immer v
¨
ollig
unabh
¨
angig vom Eingangsvektor u.
6.1.2 Beobachtbarkeit autonomer Systeme
Wir betrachten zun
¨
achst einmal autonome Systeme
˙x = f (x),
y = g(x),
290 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
d. h. zeitinvariante und von keinem Eingangsvektor u abh
¨
angige Systeme.
Um ein Beobachtbarkeitskriterium f
¨
ur sie zu entwickeln, nutzen wir die Lie-
Derivierte
L
f
g(x)=
∂g(x)
∂x
f(x)
und die mehrfache Lie-Derivierte
L
k
f
g(x)=L
f
L
k−1
f
g(x)=
∂L
k−1
f
g(x)
∂x
f(x)
zur Bestimmung von
y = L
0
f
g(x)=g(x),
˙y = L
1
f
g(x)=
∂g(x)
∂x
f(x),
.
.
.
y
(n−1)
= L
n−1
f
g(x)=L
f
L
n−2
f
g(x).
Man fasst nun die obigen Lie-Derivierten in einem Vektor
q(x)=
⎡
⎢
⎣
L
0
f
g(x)
.
.
.
L
n−1
f
g(x)
⎤
⎥
⎦
zusammen. Mit dem Vektor
z =
⎡
⎢
⎢
⎢
⎣
y
˙y
.
.
.
y
(n−1)
⎤
⎥
⎥
⎥
⎦
gilt
z = q(x).
Existiert die Umkehrfunktion q
−1
(z)=x,sokannx mit der Kenntnis
von y, ˙y,...,y
(n−1)
bestimmt werden. Aus der Kenntnis von y(t)ineinem
Intervall [t
0
,t
1
] folgt also die Kenntnis des Zustandsvektors x(t
0
). Somit gilt:
Satz 25 (Globale Beobachtbarkeit autonomer Systeme). Ein auf
D
x
⊆ IR
n
definiertes System
˙x = f (x),
y = g(x)
ist global beobachtbar, wenn die Abbildung
z = q(x)
f
¨
ur alle x ∈ D
x
eindeutig nach x aufl
¨
osbar ist.

6.1. Beobachtbarkeit nichtlinearer Systeme 291
Bei vielen nichtlinearen Systemen ist die Umkehrfunktion q
−1
nicht oder
nur sehr aufwendig zu ermitteln. Wir wollen daher nun ein einfacher hand-
habbares Kriterium f
¨
ur die lokale Beobachtbarkeit herleiten. Zu diesem Zweck
entwickeln wir q um einen Punkt x
p
herum in eine Taylor-Reihe
z = q(x
p
)+
∂q(x)
∂x
x=x
p
· (x − x
p
) + Restglied.
Unter Vernachl
¨
assigung des Restgliedes erh
¨
alt man die Gleichung
z − q(x
p
)=
∂q(x)
∂x
x=x
p
· (x − x
p
).
Aus dieser Gleichung ist direkt ersichtlich, dass aufgrund der Kenntnis von
z − q(x
p
)derZustandx rekonstruierbar, d. h. beobachtbar ist, wenn die
Jacobi-Matrix
Q(x
p
)=
∂q(x)
∂x
x=x
p
=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
∂L
0
f
g(x)
∂x
.
.
.
∂L
n−1
f
g(x)
∂x
⎤
⎥
⎥
⎥
⎥
⎥
⎦
x=x
p
den Rang n besitzt. Denn nur dann kann das lineare Gleichungssystem
z − q(x
p
)=Q(x
p
)(x − x
p
)
eindeutig nach x aufgel
¨
ost werden. Wir k
¨
onnenindiesemFallineinerUmge-
bung
U = {x
0
∈ IR
n
|||x
0
− x
p
|| <ρ}
feststellen, ob das betrachtete System beobachtbar ist. So erhalten wir auch
einen Satz
¨
uber die lokale Beobachtbarkeit.
Satz 26 (Lokale Beobachtbarkeit autonomer Systeme). Ein auf D
x
⊆
IR
n
definiertes System
˙x = f (x),
y = g(x)
ist lokal beobachtbar, wenn f
¨
ur alle x ∈ D
x
die Bedingung
rang
∂q(x)
∂x
=rang
⎛
⎜
⎜
⎜
⎜
⎜
⎝
⎡
⎢
⎢
⎢
⎢
⎢
⎣
∂L
0
f
g(x)
∂x
.
.
.
∂L
n−1
f
g(x)
∂x
⎤
⎥
⎥
⎥
⎥
⎥
⎦
⎞
⎟
⎟
⎟
⎟
⎟
⎠
= n
erf
¨
ullt ist.

292 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
Die Matrix
Q(x)=
∂q(x)
∂x
wird auch als Beobachtbarkeitsmatrix bezeichnet. Die Anwendung des Krite-
riums kann durchaus kompliziert sein, da die Matrix Q von x abh
¨
angt. Al-
lerdings ist die Rangbestimmung von Q in der Regel einfacher durchzuf
¨
uhren
als die Bestimmung der Umkehrfunktion q
−1
in Satz 25.
Satz 26 l
¨
asst sich auch direkt aus der Transformationsgleichung z = q(x)
herleiten. Gem
¨
aß dem Hauptsatz
¨
uber implizite Funktionen existiert die in-
verse Funktion q
−1
in einem Punkt x, wenn die Jacobi-Matrix Q(x)dortden
Rang n besitzt.
Um Satz 26 zu illustrieren, betrachten wir den Fall linearer Systeme
˙x = Ax,
y = c
T
x.
Wir erhalten mit g(x)=c
T
x die Beziehung
q(x)=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
L
0
f
g(x)
L
1
f
g(x)
L
2
f
g(x)
.
.
.
L
n−1
f
g(x)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
c
T
x
c
T
Ax
c
T
A
2
x
.
.
.
c
T
A
n−1
x
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
und somit die Jacobi-Matrix
Q(x)=
∂q(x)
∂x
=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
c
T
c
T
A
c
T
A
2
.
.
.
c
T
A
n−1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
. (6.2)
Besitzt die Matrix in Gl. (6.2) den Rang n, so ist das lineare System beob-
achtbar. Diese Forderung ist im linearen Fall nicht nur hinreichend, sondern es
l
¨
asst sich zeigen [123], dass sie auch notwendig ist. Sie bildet das bekannte Be-
obachtbarkeitskriterium f
¨
ur lineare Systeme, das offensichtlich ein Sonderfall
des obigen Kriteriums f
¨
ur die Beobachtbarkeit nichtlinearer Systeme ist.
6.1.3 Beispiel Synchrongenerator
Wir betrachten das Modell eines Synchrongenerators [135], wie es Bild 6.3
zeigt. Der Polradwinkel x
1
ist sowohl Zustands- als auch Ausgangsgr
¨
oße. Wei-
tere Zustandsgr
¨
oßen sind die Frequenzabweichung x
2
des Polrades gegen
¨
uber

6.1. Beobachtbarkeit nichtlinearer Systeme 293
N
S
S
N
Drehrichtung
x
1
Bild 6.3: Synchrongenerator mit blau dargestelltem Magnetfeld und Polradwinkel
x
1
.
dem Netz und die Flussverkettung x
3
des magnetischen Feldes. Die Flussver-
kettung x
3
ist nicht oder nur sehr aufwendig messbar. Man ist daher daran
interessiert, sie mittels eines Beobachters zu sch
¨
atzen. Voraussetzung hierf
¨
ur
ist die Beobachtbarkeit des Systems, die wir im Weiteren analysieren.
F
¨
ur das Zustandsraummodell gilt
˙x
1
= x
2
,
˙x
2
= b
1
− a
1
x
2
− a
2
x
3
sin x
1
−
b
2
2
sin 2x
1
,
˙x
3
= −c
1
x
3
+ c
2
cos x
1
+ c
3
,
y = x
1
.
Dabei sind a
1
, a
2
, b
1
, b
2
, c
1
, c
2
und c
3
konstante Gr
¨
oßen. Wir ermitteln
˙y =˙x
1
= x
2
,
¨y =˙x
2
= b
1
− a
1
x
2
− a
2
x
3
sin x
1
−
b
2
2
sin 2x
1
und erhalten so
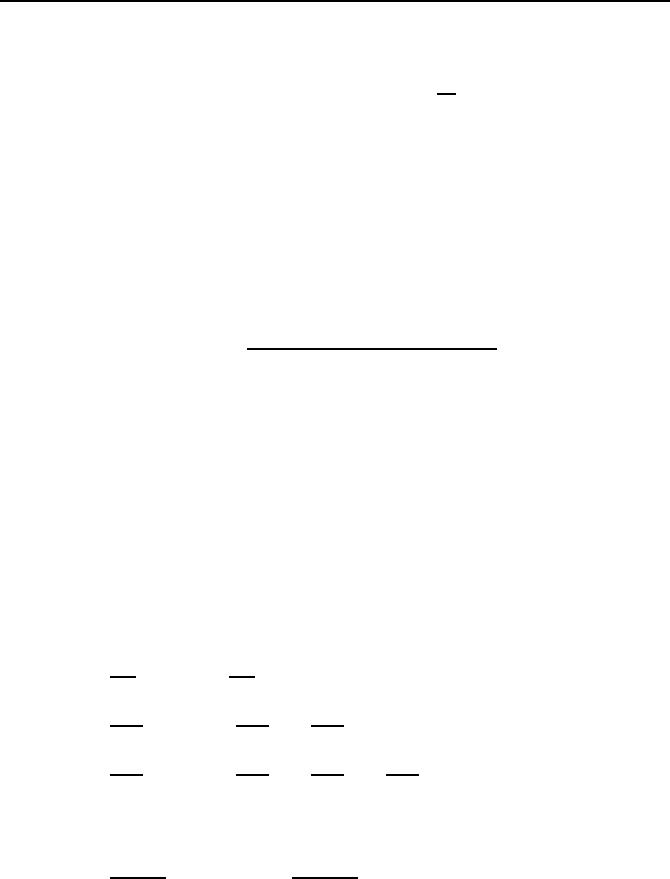
294 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
⎡
⎣
z
1
z
2
z
3
⎤
⎦
=
⎡
⎣
y
˙y
¨y
⎤
⎦
=
⎡
⎢
⎣
x
1
x
2
b
1
− a
1
x
2
− a
2
x
3
sin x
1
−
b
2
2
sin 2x
1
⎤
⎥
⎦
= q(x).
F
¨
ur den hier interessierenden Definitionsbereich
D
x
= {x ∈ IR
3
| x
1
∈ (0,π),x
2
∈ IR, x
3
∈ IR}
ist die Synchronmaschine gem
¨
aß Satz 25 global beobachtbar. Denn die Abbil-
dung z = q(x) kann durch
⎡
⎣
x
1
x
2
x
3
⎤
⎦
=
⎡
⎢
⎢
⎣
z
1
z
2
b
1
− a
1
z
2
− 0.5b
2
sin 2z
1
− z
3
a
2
sin z
1
⎤
⎥
⎥
⎦
immer f
¨
ur x ∈ D
x
eindeutig nach x aufgel
¨
ost werden.
6.1.4 Beobachtbarkeit allgemeiner nichtlinearer Systeme
Wir wollen nun nichtlineare Systeme
˙x = f (x, u),
y = g(x, u)
mit einem Eingangsvektor u betrachten. Auch hier berechnen wir, wie im Fall
autonomer Systeme, die n − 1 zeitlichen Ableitungen
˙y =
∂g
∂x
f(x, u)+
∂g
∂u
˙u = h
1
(x, u, ˙u),
¨y =
∂h
1
∂x
f(x, u)+
∂h
1
∂u
˙u +
∂h
1
∂ ˙u
¨u = h
2
(x, u, ˙u, ¨u),
...
y
=
∂h
2
∂x
f(x, u)+
∂h
2
∂u
˙u +
∂h
2
∂ ˙u
¨u +
∂h
2
∂ ¨u
...
u
= h
3
(x, u, ˙u, ¨u,
...
u
),
.
.
.
y
(n−1)
=
∂h
n−2
∂x
f(x, u)+
n−1
i=1
∂h
n−2
∂u
(i−1)
u
(i)
= h
n−1
(x, u, ˙u,...,u
(n−1)
).
¨
Ahnlich wie im Fall der Beobachtbarkeit autonomer Systeme, definieren wir
z =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
y
˙y
¨y
.
.
.
y
(n−1)
⎤
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
g(x, u)
h
1
(x, u, ˙u)
h
2
(x, u, ˙u, ¨u)
.
.
.
h
n−1
(x, u, ˙u,...,u
(n−1)
)
⎤
⎥
⎥
⎥
⎥
⎥
⎦
= q(x, u, ˙u,...,u
(n−1)
).

6.1. Beobachtbarkeit nichtlinearer Systeme 295
Auch in diesem Fall ist die eindeutige Aufl
¨
osbarkeit der Abbildung z =
q(x, u, ˙u,...,u
(n−1)
)nachx ausschlaggebend f
¨
ur die Beobachtbarkeit des
Systems. Es gilt folgendes hinreichendes Kriterium.
Satz 27 (Globale Beobachtbarkeit nichtlinearer Systeme). Ein auf
D
x
⊆ IR
n
und C
u
⊆ C
n−1
definiertes System
˙x = f (x, u),
y = g(x, u)
ist global beobachtbar, wenn die Abbildung
z = q(x, u, ˙u,...,u
(n−1)
)
f
¨
ur alle x ∈ D
x
und u ∈ C
u
eindeutig nach x aufl
¨
osbar ist.
Auch hier ist die praktische Anwendung des Satzes schwierig. Denn nur in
einfachen F
¨
allen l
¨
asst sich die Umkehrfunktion
x = q
−1
(z, u, ˙u,...,u
(n−1)
)
bestimmen.
Einfacher als die
¨
Uberpr
¨
ufung der globalen Beobachtbarkeit kann wieder
die
¨
Uberpr
¨
ufung der lokalen Beobachtbarkeit ausfallen. Analog zum Fall au-
tonomer Systeme l
¨
asst sich hierzu folgender hinreichender Satz herleiten:
Satz 28 (Lokale Beobachtbarkeit nichtlinearer Systeme). Ein auf
D
x
⊆ IR
n
und C
u
⊆ C
n−1
definiertes System
˙x = f (x, u),
y = g(x, u)
ist lokal beobachtbar, wenn f
¨
ur alle x ∈ D
x
und u ∈ C
u
die Bedingung
rang
∂q(x, u, ˙u,...,u
(n−1)
)
∂x
=rang
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
∂g(x, u)
∂x
∂h
1
(x, u, ˙u)
∂x
∂h
2
(x, u, ˙u, ¨u)
∂x
.
.
.
∂h
n−1
(x, u, ˙u,...,u
(n−1)
)
∂x
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
= n
erf
¨
ullt ist.
Satz 28 kann anders als Satz 27 zumindest punktuell auf einfache Weise
angewendet werden, indem man den Rang bzw. die Determinante der Beob-
achtbarkeitsmatrix
Q(x, u, ˙u,...,u
(n−1)
)=
∂q(x, u, ˙u,...,u
(n−1)
)
∂x
an vorgegebenen St
¨
utzstellen (x, u, ˙u,...,u
(n−1)
) berechnet.

296 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
6.1.5 Nichtlineare Beobachtbarkeitsnormalform
Wir wollen ein global beobachtbares System
˙x = f (x, u), (6.3)
y = g(x, u)
betrachten. Nehmen wir an, dass es uns gelungen ist, die Abbildung
z = q(x, u, ˙u,...,u
(n−1)
) (6.4)
und ihre Inverse
x = q
−1
(z, u, ˙u,...,u
(n−1)
) (6.5)
zu ermitteln. Dann ist es m
¨
oglich, die Systemdarstellung (6.3) mittels der
Abbildung (6.5) bzw. (6.4) und mit
h
n
(x, u, ˙u,...,u
(n)
)=
∂h
n−1
∂x
f(x, u)+
n
i=1
∂h
n−1
∂u
(i−1)
u
(i)
in die Darstellung
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
˙z
1
˙z
2
.
.
.
˙z
n−1
˙z
n
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
˙y
¨y
.
.
.
y
(n−1)
y
(n)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
z
2
z
3
.
.
.
z
n
h
n
q
−1
(z, u, ˙u,...,u
(n−1)
), u, ˙u,...,u
(n)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
y = z
1
zu
¨
uberf
¨
uhren. Wir k
¨
urzen noch
ϕ
z, u, ˙u,...,u
(n)
!
= h
n
q
−1
(z, u, ˙u,...,u
(n−1)
), u, ˙u,...,u
(n)
!
ab und erhalten
˙z =
⎡
⎢
⎢
⎢
⎣
z
2
.
.
.
z
n
ϕ
z, u, ˙u,...,u
(n)
⎤
⎥
⎥
⎥
⎦
, (6.6)
y = z
1
.
Die zur Darstellung (6.3) alternative Systemdarstellung (6.6) wird als
nichtlineare Beobachtbarkeitsnormalform bezeichnet. Bild 6.4 zeigt das zu-
geh
¨
orige Strukturbild. Liegt ein System in dieser Form vor, so kann man
