J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.

6.1. Beobachtbarkeit nichtlinearer Systeme 297
ϕ(z, u, ˙u,...,u
(n)
)
1
s
1
s
1
s
1
s
˙z
n
z
n
z
n−1
z
3
z
2
y = z
1
...
...
u
˙u
u
(n)
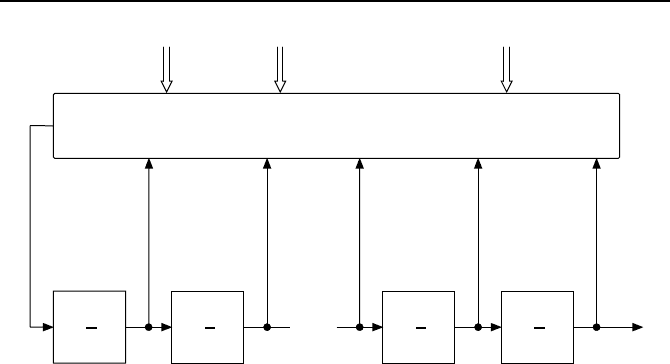
Bild 6.4: System in Beobachtbarkeitsnormalform.
direkt aus den Systemgleichungen auf die Beobachtbarkeit schließen. Denn
¨
uber die Integriererkette in Gl. (6.6) wirken alle Zust
¨
ande z
i
auf den Aus-
gangswert y = z
1
und aus dem Ausgangswert y und seinen Ableitungen y
(i)
k
¨
onnen alle Zustandswerte z
i
ermittelt werden. Ein System, das in nichtlinea-
rer Beobachtungsnormalform vorliegt, ist folglich immer global beobachtbar.
Des Weiteren kann jedes global beobachtbare System in die Beobachtungs-
normalform transformiert werden.
6.1.6 Beobachtbarkeit eingangslinearer Systeme
Wir betrachten nun eingangslineare Systeme
˙x = a(x)+b(x)u,
y = c(x).
(6.7)
Wie im allgemeineren Fall ˙x = f (x, u),y= g(x, u) des Abschnittes 6.1.4,
bestimmen wir
y = c(x),
˙y = L
a
c(x)+L
b
c(x)u,
¨y = L
2
a
c(x)+L
b
L
a
c(x)u + L
a
L
b
c(x)u + L
2
b
c(x)u
2
+ L
b
c(x)˙u,
.
.
.
y
(n−1)
= L
n−1
a
c(x)+L
b
L
n−2
a
c(x)u + ...+ L
n−1
b
c(x)u
n−1
+ L
b
c(x)u
(n−2)
.
So erhalten wir die Transformationsgleichung
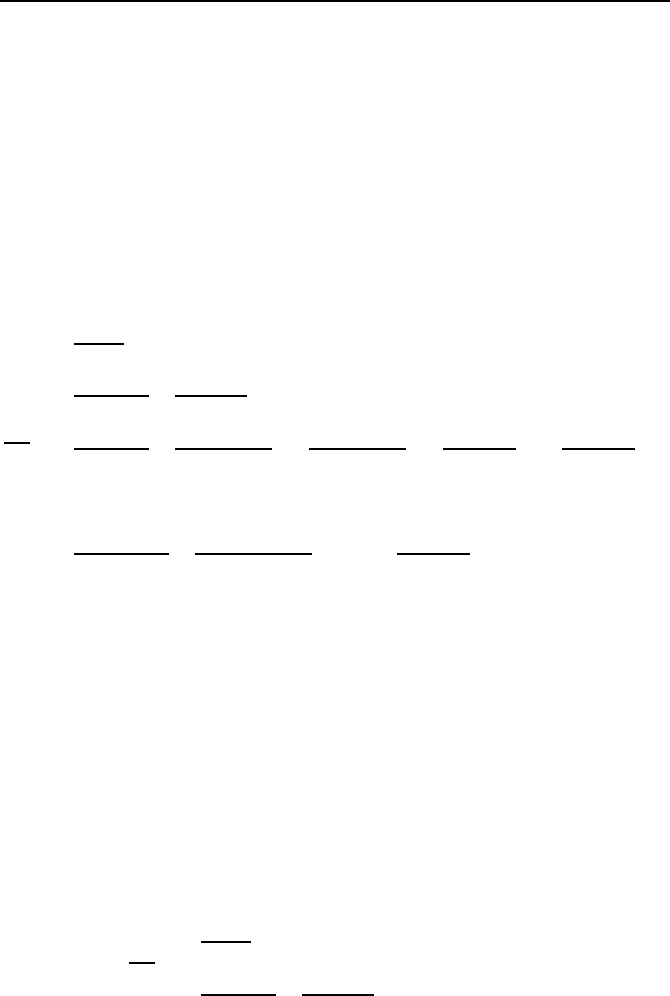
298 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
z =
⎡
⎢
⎢
⎢
⎣
y
˙y
.
.
.
y
(n−1)
⎤
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎣
c(x)
L
a
c(x)+L
b
c(x)u
.
.
.
L
n−1
a
c(x)+...+ L
b
c(x)u
(n−2)
⎤
⎥
⎥
⎥
⎦
= q(x,u, ˙u,...,u
(n−2)
).
Wir sahen schon in Kapitel 4.2, dass die Terme L
b
L
k−1
a
c(x) identisch null
sind f
¨
ur alle k<δ.Dabeiistδ die Differenzordnung des Systems (6.7).
Wir k
¨
onnen die Beobachtbarkeit des Systems (6.7) anhand der Eindeutig-
keit der Abbildung q bzw. ihrer Jacobi-Matrix untersuchen. Dazu lassen sich
die S
¨
atze 27 und 28 verwenden.
Wir erhalten f
¨
ur die Jacobi-Matrix
∂q
∂x
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
∂c(x)
∂x
∂L
a
c(x)
∂x
+
∂L
b
c(x)
∂x
u
∂L
2
a
c(x)
∂x
+
∂L
b
L
a
c(x)
∂x
u +
∂L
a
L
b
c(x)
∂x
u +
∂L
2
b
c(x)
∂x
u
2
+
∂L
b
c(x)
∂x
˙u
.
.
.
∂L
n−1
a
c(x)
∂x
+
∂L
b
L
n−2
a
c(x)
∂x
u + ...+
∂L
b
c(x)
∂x
u
(n−2)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
Die Erf
¨
ullbarkeit der Rangbedingung rang (∂q/∂x)=n des Satzes 28 ist
auch hier von u abh
¨
angig. Offensichtlich kann es Eingangssignale u geben, so
dass die Rangbedingung nicht erf
¨
ullt ist und das System nicht beobachtbar
ist. Allerdings kann mittels Satz 28 keine Aussage
¨
uber die Beobachtbarkeit
getroffen werden, wenn die Rangbedingung nicht erf
¨
ullt ist. Denn Satz 28 ist
nur hinreichend.
Wir betrachten das einfache Beispiel
˙x
1
= −x
2
+ x
2
u,
˙x
2
= −x
1
,
y = x
1
.
(6.8)
Es gilt
∂q
∂x
=
⎡
⎢
⎢
⎣
∂c(x)
∂x
∂L
a
c(x)
∂x
+
∂L
b
c(x)
∂x
u
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
10
0 u − 1
⎤
⎥
⎥
⎦
.
F
¨
ur u =1istrang(∂q/∂x) = 2 und das System lokal beobachtbar. Ist u =
1, so hat ∂q/∂x nur den Rang eins. In der Tat ist das System (6.8) nicht
beobachtbar f
¨
ur u =1,denndanngilt

6.2. Luenberger-Beobachter f
¨
ur nichtlineare Regelkreise 299
˙x
1
=0,
˙x
2
= −x
1
,
y = x
1
und f
¨
ur dieses System kann man aus der Kenntnis von y und u den Wert von
x
2
nicht bestimmen. Mittels des notwendigen und hinreichenden Beobacht-
barkeitskriteriums f
¨
ur lineare Systeme l
¨
asst sich dies auch zeigen, denn die
Beobachtbarkeitsmatrix aus Gl. (6.2) f
¨
ur obiges System,
c
T
c
T
A
=
10
00
,
besitzt nur den Rang eins.
F
¨
ur eingangslineare Systeme (6.7), die den relativen Grad n aufweisen und
durch einen Diffeomorphismus z = q(x)=t(x)indieForm
⎡
⎢
⎢
⎢
⎣
˙z
1
.
.
.
˙z
n−1
˙z
n
⎤
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎣
z
2
.
.
.
z
n
L
n
a
c(t
−1
(z)) + L
b
L
n−1
a
c(t
−1
(z))u
⎤
⎥
⎥
⎥
⎦
gebracht werden k
¨
onnen, ist die Frage nach ihrer Beobachtbarkeit leicht zu
beantworten. Denn sie liegen in nichtlinearer Beobachtbarkeitsnormalform vor
und sind daher immer global beobachtbar.
6.2 Luenberger-Beobachter f
¨
ur nichtlineare Regelkreise
Die Beobachtertheorie von D. G. Luenberger wurde f
¨
ur lineare Systeme ent-
wickelt. F
¨
ur den Fall eines Regelkreises mit linearer Regelstrecke
˙x = Ax + Bu,
y = Cx
und nichtlinearem Regler
u = h(x, w),
also einem nichtlinearen Regelkreis mit der Systembeschreibung
˙x = Ax + Bh(x, w),
kann ebenfalls ein Luenberger-Beobachter zum Einsatz kommen [122]. Wie im
linearen Fall, besteht er aus einem Streckenmodell und einem R
¨
uckkopplungs-
system, das wie ein Regler wirkt:
˙
˜x = A˜x + Bu
Modell
+ L(y − C ˜x)
R
¨
uckkopplungssystem
.
300 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
DieAufgabedesR
¨
uckkopplungssystems L (y − C ˜x) ist es, den Sch
¨
atzfehler
e = x − ˜x,
d. h. die Differenz von Streckenzustand x und Beobachterzustand ˜x,asympto-
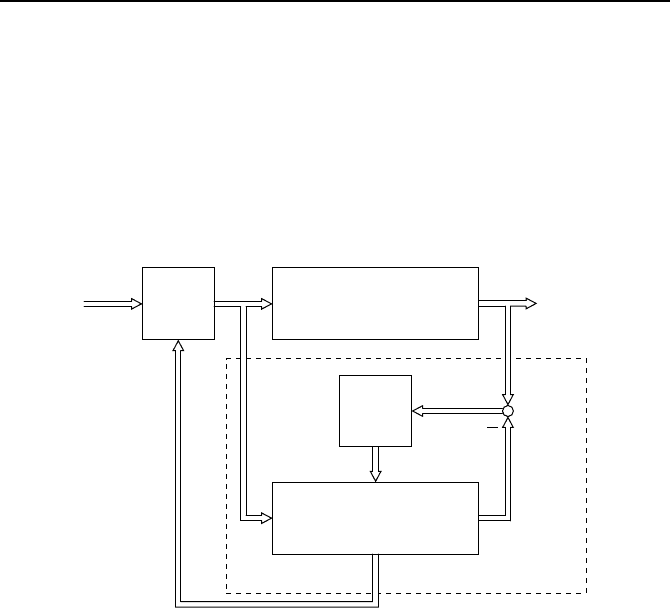
tisch abklingen zu lassen. Bild 6.5 zeigt die Struktur des Regelungssystems
mit Beobachter und nichtlinearem Regelgesetz u = h(˜x, w).
v
w
h(˜x, w)
u
y
˜y
y − ˜y
˙x = Ax+ Bu
y = Cx
˜x
˙
˜x = A ˜x+Bu+v
˜y = C ˜x
L
Beobachter
Regler
Regelstrecke
Bild 6.5: Struktur des Systems mit linearer Regelstrecke, nichtlinearem Regler und
linearem Beobachter.
Ohne Einschr
¨
ankung der Allgemeinheit ist es im Falle eines konstanten
F
¨
uhrungsgr
¨
oßenvektors w m
¨
oglich, das Regelungssystem so zu transformie-
ren, dass w = 0 gilt. Man kann dann von einem Regler
u = h(˜x)
ausgehen, was im Folgenden auch geschieht.
Zusammengefasst gilt folgender Satz von D. G. Luenberger.
Satz 29 (Luenberger-Beobachter f
¨
ur nichtlineare Regelkreise). Ge-
geben sei das Regelungssystem
˙x = Ax + Bu, y = Cx,
u = h(x)
mit der global (lokal) asymptotisch stabilen Ruhelage x
R
= 0. Die Vektorfunk-
tion h erf
¨
ulle die Lipschitz-Bedingung

6.3. Beobachterentwurf mittels Linearisierung 301
||h(x
1
) − h(x
2
)|| ≤ k ·||x
1
− x
2
||
f
¨
ur alle x
1
, x
2
∈ IR
n
(f
¨
ur alle x
1
, x
2
aus einer Umgebung U ⊂ IR
n
von x
R
=0)
und ein k>0.F
¨
ugt man dann einen asymptotisch stabilen, linearen Beob-
achter in das Regelungssystem ein, d. h., hat das Gesamtsystem die Form
˙x = Ax + Bu, y = Cx,
u = h(˜x),
˙
˜x = A˜x + Bu + L(y − C ˜x),
so besitzt dieses System ebenfalls eine global (lokal) asymptotisch stabile Ru-
helage in
x
T
˜x
T
= 0
T
.
Funktionen, die die Lipschitz-Bedingung erf
¨
ullen, heißen lipschitzstetig.
Differenzierbare Funktionen sind genau dann lipschitzstetig, wenn ihre Ablei-
tungen beschr
¨
ankt sind. Typische Anwendungsf
¨
alle f
¨
ur Satz 29 sind die Rege-
lungen aus Kapitel 3, d. h. strukturvariable Regelungen oder S
¨
attigungsregler.
6.3 Beobachterentwurf mittels Linearisierung
6.3.1 Funktionsweise und Entwurf
Wir bleiben auch in diesem Kapitel gedanklich beim Luenberger-Beobachter
und wollen von seiner Grundidee bei der Entwicklung eines Beobachters f
¨
ur
nichtlineare Systeme profitieren.
Betrachtet man ein lineares System
˙x = Ax + Bu,
y = Cx
mit Beobachter
˙
˜x = A˜x + Bu + L(y − C ˜x),
so liegt der Gedanke nahe, dieses Schema auf nichtlineare Systeme
˙x = f (x, u),
y = g(x)
zu
¨
ubertragen. Der Beobachter hat dann die Form
˙
˜x = f (˜x, u)+L(y − g(˜x)).
F
¨
ur den Beobachterfehler
e = x − ˜x
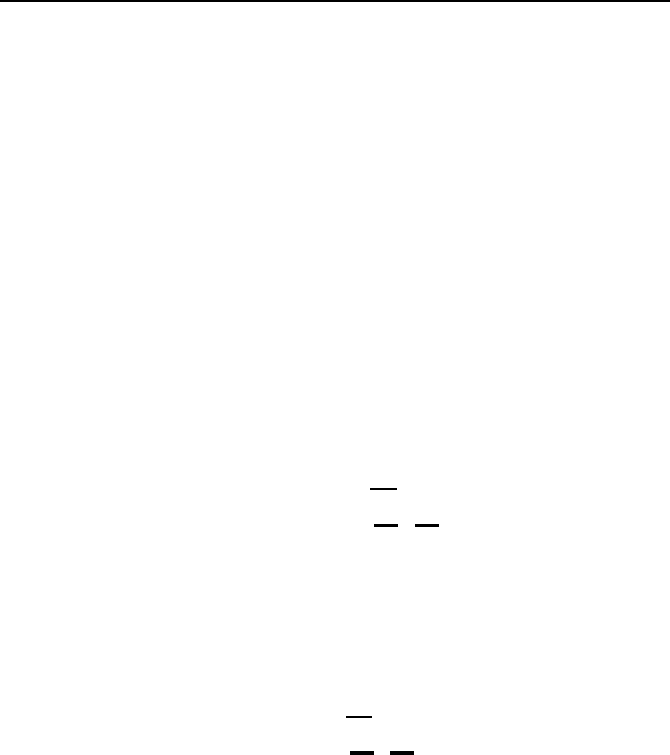
302 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
gilt
˙e = f(˜x + e, u) − f (˜x, u) − L(y − g(˜x)).
Man erh
¨
alt also eine nichtlineare Differenzialgleichung f
¨
ur den Beobachterfeh-
ler. Ersetzt man noch
y = g(x)=g(˜x + e)
in ihr, so ergibt sich
˙e = f (˜x + e, u) − f(˜x, u) − L(g(˜x + e) − g(˜x)). (6.9)
Damit der Beobachterfehler e asymptotisch abklingt, steht man vor der
Entwurfsaufgabe, die obige nichtlineare Systemgleichung (6.9) mittels L so
auszulegen, dass in e = 0 eine asymptotisch stabile Ruhelage vorliegt.
DieeinfachsteVorgehensweisef
¨
ur den Entwurf der Beobachtermatrix
L f
¨
uhrt
¨
uber die Linearisierung der Gleichung (6.9). Mittels einer Taylor-
Entwicklung linearisiert man um einen festen Punkt ˜x
p
und erh
¨
alt
f(˜x
p
+ Δ˜x + e, u)=f(˜x
p
, u)+
∂f
∂ ˜x
˜x=˜x
p
A
·(Δ˜x + e)+...,
wobei wir u als Systemparameter auffassen. Des Weiteren gilt
f(˜x
p
+ Δ˜x, u)=f(˜x
p
, u)+A · Δ˜x + ...
F
¨
ur die Ausgangsvektorfunktion g erh
¨
alt man ganz
¨
ahnlich
g(˜x
p
+ Δ˜x + e)=g(˜x
p
)+
∂g
∂ ˜x
˜x=˜x
p
C
·(Δ˜x + e)+...,
sowie
g(˜x
p
+ Δ˜x)=g(˜x
p
)+C · Δ˜x + ...
Setzt man obige Taylor-Entwicklungen – abgebrochen nach der ersten Ablei-
tung – in die Beobachtergleichung (6.9) ein, so ergibt sich
˙e ≈ (A − LC) · e, (6.10)
d. h. die Sch
¨
atzgleichung des linearen Beobachters. Dabei ist zu ber
¨
ucksichti-
gen, dass Gl. (6.10) aufgrund der Vernachl
¨
assigung h
¨
oherer Ableitungen in
den Taylor-Reihen nur eine N
¨
aherung darstellt.
Legt man die Matrix A − LC des Beobachters stabil aus, so wird auch
der Beobachterfehler e f
¨
ur t →∞gegen null streben. Die Situation
¨
ahnelt

6.3. Beobachterentwurf mittels Linearisierung 303
also der linearer Systeme mit linearen Beobachtern. Allerdings gilt diese Stabi-
lit
¨
atsaussage aufgrund obiger N
¨
aherung nur in einer mehr oder weniger großen
Umgebung des Linearisierungspunktes ˜x
p
.
Will man zu besseren, weitreichenderen Ergebnissen kommen, so kann man
die oben beschriebene Linearisierung in Abh
¨
angigkeit von ˜x und u vornehmen,
d. h., die Systemmatrix
A(˜x, u)=
∂f(˜x, u)
∂ ˜x
und die Ausgangsmatrix
C(˜x)=
∂g(˜x)
∂ ˜x
sind nicht mehr konstant, sondern vom Arbeitspunkt abh
¨
angig.
Des Weiteren w
¨
ahlt man nun die Beobachtermatrix L als Funktion von ˜x
und u zu L(˜x, u). So ergibt sich anstelle der linearen Sch
¨
atzfehlergleichung
˙e =(A − LC) · e
des Beobachters eine von ˜x und u abh
¨
angige nichtlineare Gleichung
˙e =(A(˜x, u) − L(˜x, u)C(˜x)) · e,
die ein Kontinuum von Arbeitspunkten ber
¨
ucksichtigt und entsprechend ef-
fektiver sein kann.
Ziel ist es nun, die Systemmatrix
F (˜x, u)=A(˜x, u) − L(˜x, u)C(˜x
)
der Sch
¨
atzfehlergleichung durch geeignete Wahl von L(˜x, u) konstant auszu-
legen. Dies geschieht so, dass alle Eigenwerte von F negative Realteile auf-
weisen. In diesem Fall gilt
˙e = Fe
und der Sch
¨
atzfehler e klingt asymptotisch ab.
Der einfachste Weg, eine konstante Matrix F zu erhalten, ist L(˜x, u)f
¨
ur ei-
ne vorgegebene Matrix F aus L(˜x, u)=(A(˜x, u) − F ) C
−1
(˜x) zu berechnen.
Dies ist allerdings nur f
¨
ur eine invertierbare Matrix C(˜x)m
¨
oglich. Vorausset-
zung f
¨
ur die Invertierbarkeit von C ist, dass
C(˜x)=
∂g(˜x)
∂ ˜x
eine quadratische Matrix ist. Dies wiederum setzt voraus, dass g(˜x)einen -di-
mensionale Funktion ist, es also genauso viele Ausgangsvariablen wie Zust
¨
ande
gibt. Dieser Fall ist in der Praxis eher selten anzutreffen und daher in der Regel
nicht von Bedeutung.
Daher geht man einen anderen Weg: Man berechnet das charakteristische
Polynom von F ,

304 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
P (s)=det(sI −F (˜x, u))
=det(sI − A(˜x, u)+L(˜x, u)C(˜x))
=
n
9
i=1
(s + λ
i
),
und fordert, dass die Realteile aller Eigenwerte λ
i
negativ sind. Hierbei ist zu
beachten, dass die Eigenwerte λ
i
bzw. die Koeffizienten von P sowohl von ˜x
als auch von u unabh
¨
angig sind. Um sicherzustellen, dass alle Re {λ
i
} < 0
sind, muss man die Beobachtermatrix L(˜x, u) entsprechend auslegen.
F
¨
ur die Berechnung der Beobachtermatrix L(˜x, u)betrachtetmandas
charakteristische Polynom
P (s)=s
n
+ a
n−1
(L, ˜x, u)s
n−1
+ ...+ a
0
(L, ˜x, u)
und fordert, dass es einem Wunschpolynom
ˆ
P (s)=s
n
+ˆa
n−1
s
n−1
+ ...+ˆa
0
entspricht. Hierbei soll
ˆ
P nat
¨
urlich nur Nullstellen mit negativem Realteil auf-
weisen. Durch Koeffizientenvergleich erh
¨
alt man ein nichtlineares Gleichungs-
system
a
n−1
(L, ˜x, u)=ˆa
n−1
,
a
n−2
(L, ˜x, u)=ˆa
n−2
,
.
.
.
a
0
(L, ˜x, u)=ˆa
0
mit n Gleichungen und n · r Unbekannten, den Elementen der n ×r -Matrix
L. Dabei ist, wir erinnern uns, n die Systemordnung und r die Dimension des
Ausgangsgr
¨
oßenvektors y.
Die L
¨
osung des obigen Gleichungssystems stellt sicher, dass die Eigen-
werte von F konstant sind und den Nullstellen des Wunschpolynoms
ˆ
P (s)
entsprechen. Diese Tatsache garantiert allerdings nicht die Einhaltung der
urspr
¨
unglichen Forderung, dass die Systemmatrix
F (˜x, u)=A(˜x, u) − L(˜x, u)C(˜x) (6.11)
der linearisierten Beobachtergleichung konstant ist, d. h. unabh
¨
angig von ˜x
und u.
Die Konstanz von F muss vielmehr durch Einsetzen des berechneten
L(˜x, u) in Gleichung (6.11)
¨
uberpr
¨
uft werden. Sollte sich dabei herausstel-
len, dass F nicht unabh
¨
angig von ˜x und u ist, so kann der Beobachter
˙
˜x = f(˜x, u)+L(˜x, u) · (y − g(˜x))
6.3. Beobachterentwurf mittels Linearisierung 305
trotzdem verwendet werden, wenn die Elemente von F nicht sehr stark va-
riieren. Eine Absicherung der Funktionsweise durch Simulation ist in diesem
Fall unumg
¨
anglich.
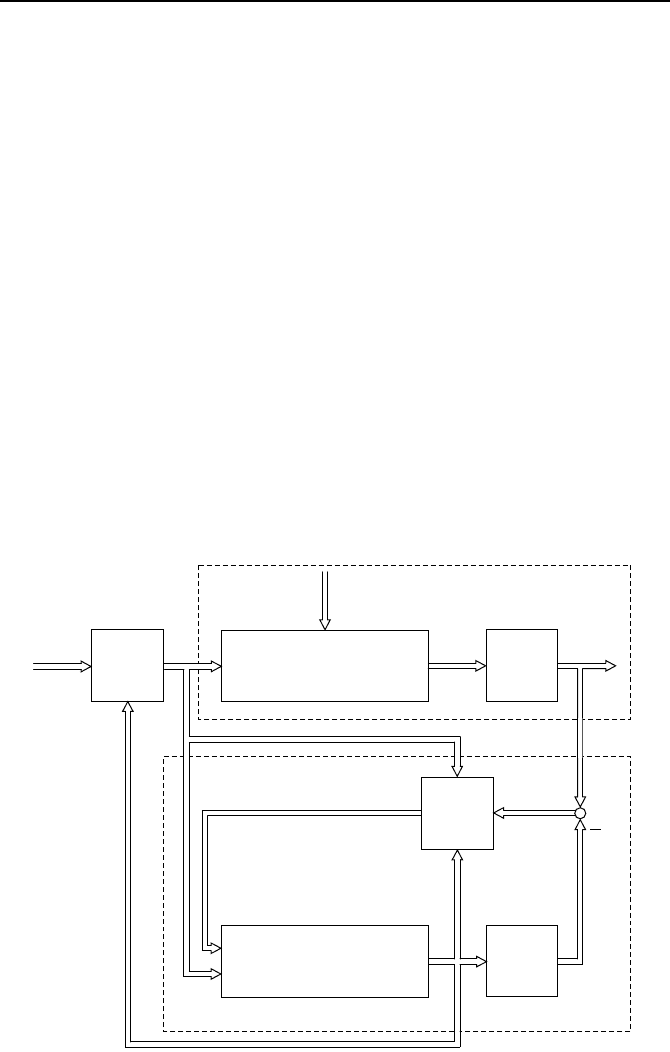
6.3.2 Regelkreis mit Beobachter
F
¨
ugt man den oben entwickelten Beobachter in einen nichtlinearen Regel-
kreis ein, so ergibt sich eine
¨
ahnliche Struktur wie im Fall des Luenberger-
Beobachters im linearen Regelkreis. Bild 6.6 zeigt sie. Allerdings ist L im
nichtlinearen Fall nicht konstant, sondern eine Funktion von ˜x und u.
Die zugeh
¨
origen Gleichungen des Regelkreises mit Beobachter lauten:
˙x = f(x, u),
y = g(x),
(
Regelstrecke
u = h(˜x, w),
'
Regler
˙
˜x = f (˜x, u)+L(˜x, u) · (y − g(˜x)).
'
Beobachter
Alternativ zu dieser Darstellung k
¨
onnen die Gleichungen des Gesamtsystems
auch mittels des Sch
¨
atzfehlers
e = x − ˜x
w
u
x
˜x ˜x
y
e
v
x(0)
Regelstrecke
Beobachter
L(˜x, u)
h(˜x, w)
g(x)
g(˜x)
˙x = f (x, u)
˙
˜x = f (˜x, u)+v
Bild 6.6: Struktur der Regelstrecke mit Beobachter und Regler h(˜x, w).

306 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
dargestellt werden. Es gilt
˙x = f(x, u),
y = g(x),
u = h(x − e, w),
˙e = F (x − e, u)e.
Allerdings eignet sich diese Darstellung nicht f
¨
ur eine Realisierung, da der Be-
obachterfehler e aufgrund der Unkenntnis von x nicht gebildet werden kann.
Die zuletzt gezeigten Gleichungen des Systems lassen aber eine Plausibi-
lit
¨
atsbetrachtung bez
¨
uglich der Stabilit
¨
at zu. Da F n
¨
aherungsweise konstant
ist und Eigenwerte mit negativem Realteil besitzt, gilt
e → 0 f
¨
ur t →∞.
Dann wird f
¨
ur das Regelgesetz f
¨
ur große Werte t ebenfalls
u = h(x − e, w) ≈ h(x, w)
gelten. Ist der Regelkreis ohne Beobachter stabil, so ist es plausibel (aber nicht
bewiesen), dass auch der Regelkreis mit Beobachter stabil ist.
6.3.3 Beispiel Bioreaktor
Als Beispiel wird ein Bioreaktor [68] betrachtet. Bioreaktoren werden zur
Herstellung von Vitaminen und Medikamenten eingesetzt. Dazu wird in ei-
nem ersten Schritt eine Zellkultur gez
¨
uchtet, die in weiteren Schritten f
¨
ur die
Herstellung des eigentlich gew
¨
unschten Stoffes benutzt wird. Hier wird die
Wachstumsphase der Zellkultur modelliert.
Der Reaktor hat ein konstantes Volumen.
¨
Uber eine Pumpe wird Glu-
cose als Substrat in den Bioreaktor gegeben. Die angesetzte Zellkultur ver-
mehrt sich unter Verbrauch des Substrates und vergr
¨
oßert so ihre Biomasse.
Ein R
¨
uhrer sorgt f
¨
ur eine gleichm
¨
aßige Durchmischung. Das Gemisch wird
schließlich aus dem Reaktor f
¨
ur weitere Prozessschritte entnommen. Bild 6.7
illustriert den Prozess.
Die Biomassekonzentration x
1
der Zellkultur, gemessen in g l
−1
,steigtpro-
portional zu ihrem Bestand mit
˙x
1
= μ(x
2
) · x
1
.
Es liegt also ein klassisches Wachstumsgesetz vor. Die Wachstumskonstante μ
h
¨
angt von der Konzentration x
2
des Wachstumssubstrats, d. h. der Glucose,
gem
¨
aß der folgenden Wachstumskinetik
μ(x
2
)=
μ
0
· x
2
k
1
+ x
2
+ k
2
x
2
2
