J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

276 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

5.3.4 Defuzziﬁzierung

Das Ergebnis μ

res

der Inferenz ist, wie oben festgestellt, nicht direkt nutzbar.

Man ben

otigt in der Praxis im Allgemeinen einen Zahlenwert. Somit steht

man vor der Aufgabe, aus der Fuzzy-Menge μ

res

einen Zahlenwert, der f

das Auswertungsergebnis repr

asentativ ist, zu bestimmen. Sozusagen einen

Kompromiss- oder Mittelwert. Dieser Vorgang heißt Defuzziﬁzierung.

Der Fl

achenschwerpunkt, genauer seine y-Koordinate

res

∞



−∞

y · μ

res

, ..., x

,y) dy

∞



−∞

res

, ..., x

,y) dy

ist ein solcher Wert. Er bildet das Endergebnis, d. h. den Ausgangswert der

gesamten Regelbasisauswertung. Bild 5.29 zeigt ein Beispiel hierf

ur. Dieses

Verfahren der Defuzziﬁzierung, dass die bekannteste Defuzziﬁzierungsmethode

bildet, wird als Fl

achenschwerpunktsmethode oder COA-Verfahren bezeichnet

(engl. Abk. f

”

center of area“).

Die Bestimmung des Fl

achenschwerpunktes ist allerdings aufwendig, da

die betrachtete Zugeh

origkeitsfunktion μ

res

die Form eines vielteiligen Poly-

gonzuges aufweist. Man kann die Berechnung des Fl

achenschwerpunktes y

res

aber wesentlich vereinfachen, indem man f

ur die Zugeh

origkeitsfunktionen der

linguistischen Werte LW

von y keine Trapeze oder Dreiecke w

ahlt, sondern

Singletons. Singletons μ

(y) nehmen nur an einer Stelle y

den Funktions-

wert eins an und sonst

uberall den Funktionswert null, d. h.

(y)=



ur y = y

0sonst.

Bild 5.30 zeigt exemplarisch einen Singleton.

Das Ergebnis der Akkumulation nimmt dann die in Bild 5.31 beispiel-

haft dargestellte Form an. Die Einzelergebnisse der Akkumulation

uberlagern

sich in diesem Fall also nicht mehr zu einem Polygonzug. Und man kann die

Zugeh

origkeitsfunktion μ

res

zerlegen in

res

= μ

res,1

+ μ

res,2

+ μ

res,3

+ ...

Dabei sind die Zugeh

origkeitsfunktionen μ

res,i

die akkumulierten Ergebnisse

all derjenigen Regeln, die auf den Singleton i wirken.

ur den Fall, dass alle m Ausgangszugeh

origkeitsfunktionen Singletons

sind, ist der Fl

achenschwerpunkt, der dann korrekterweise kein Fl

achenschwer-

punkt mehr ist, sondern ein Mittelwert, einfach zu berechnen. Man erh

alt

5.3. Fuzzy-Control 277

res

Bild 5.30: Singleton.

res

halb

auf

res,1

res,2

res,3

50%

62.5% 100%

Bild 5.31: Defuzziﬁzierung im Fall von Singletons.

res



i=1

s,i

· μ

res,i

, ..., x

)



i=1

res,i

, ..., x

)

Dieser Abk

ommling der Fl

achenschwerpunktsmethode COA wird allgemein

als COS-Verfahren bezeichnet (engl. Abk. f

”

center of singletons“). Das Bei-

spiel einer Ventilstellung aus Bild 5.31 mit den drei Zugeh

origkeitsfunktionen

zu, halb und auf illustriert die Defuzziﬁzierungsmethode. Als Ergebnis erh

alt

man mit μ

res,1

=0,μ

res,2

=0.75 und μ

res,3

=0.25 in diesem Fall

res

50 · 0.75 + 100 ·0.25

0.75 + 0.25

%=62.5%

als Ergebnis der Defuzziﬁzierung.

5.3.5 Fuzzy-Systeme und Fuzzy-Regler

Mittels Fuzziﬁzierung, Aggregation, Implikation, Akkumulation und Defuzzi-

ﬁzierung k

onnen wir mit den Ergebnissen der vorherigen Abschnitte sprach-

lich formulierte Regeln in eine mathematische Funktion umformen. Bild 5.32

illustriert dies.

Diese Funktion

res

= f(x

, ..., x

)

ist mehrfach verkettet, wobei im Detail die Verkettung aus folgenden Teil-

funktionen resultiert:

Wenn ..., dann ...

Fuzzy-Logik

, ..., x

) = min{...}

res

, ..., x

,y) = max{...}

res

y · μ

res

(y)dy

res

(y)dy

Bild 5.32: Umwandlung von Regeln in Gleichungen mittels Fuzzy-Logik.

278 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

Fuzziﬁzierung: Bestimmung aller Zugeh

origkeitswerte μ

i,j

Aggregation: μ

agg,k

, ..., x

)=min{μ

1,i

), ..., μ

n,l

)},

k =1, ..., m,

Implikation: μ

, ..., x

,y)=min{μ

agg,k

, ..., x

),μ

(y)},

k =1, ..., m,

Akkumulation: μ

res

, ..., x

,y)=max{μ

, ..., x

,y), ...,

, ..., x

,y)},

Defuzziﬁzierung: y

res

∞



−∞

y · μ

res

, ..., x

,y) dy

∞



−∞

res

, ..., x

,y) dy

Bei der Berechnung von y

res

ur eine Situation (x

, ..., x

)arbeitetmanobige

Listeab.MankanndieVariablenx

, ..., x

als Eingangsvariablen und y als

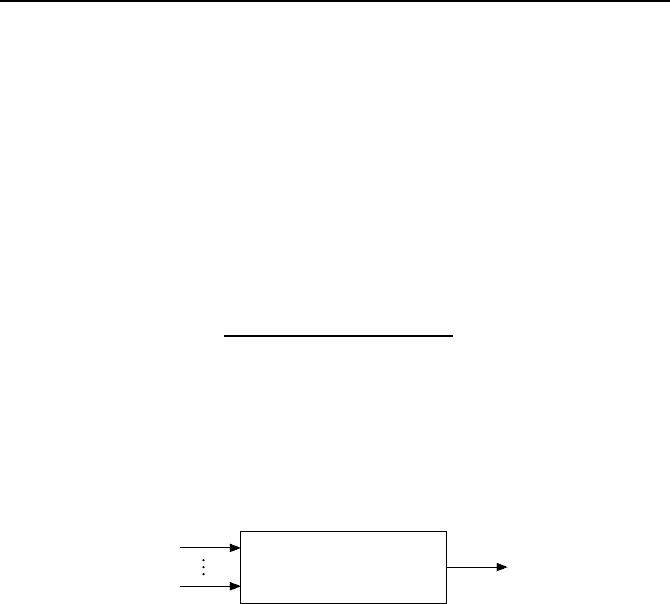
Ausgangsvariable eines Systems auﬀassen, wie es Bild 5.33 zeigt.

Fuzzy-System

y = f(x

, ..., x

)

Bild 5.33: Fuzzy-System.

Die Anwendungsm

oglichkeiten von Fuzzy-Systemen sind sehr groß. Dies

ist darauf zur

uckzuf

uhren, dass mittels Fuzzy-Logik viele menschliche Verhal-

tensweisen durch eine mathematische Funktion beschreibbar sind. Wichtige

Anwendungsgebiete sind, wie bereits erw

ahnt, Steuerungen und Regelungen.

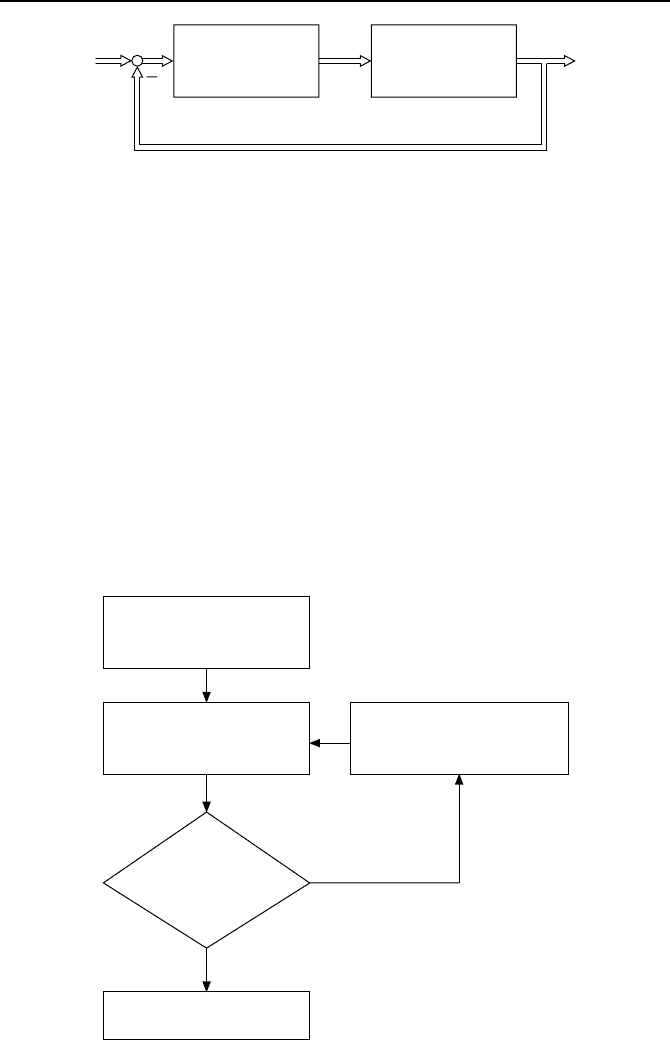
Dieser Zweig der Fuzzy-Logik heißt Fuzzy-Control [46, 69, 201]. Bild 5.34 zeigt

einen solchen mit einem Fuzzy-Regler ausgestatteten Regelkreis.

In vielen Anwendungsbereichen kann menschliches Verhalten nachgebildet

werden. Beispiele sind die Regelung von Kl

aranlagen [134], ABS-Bremssysteme

[129], die Regelung von U-Bahnen [179], die Regelung von Papiermaschinen

[2], ein Alarmsystem f

ur die An

asthesie [190], die Autofokussteuerung bei

Kameras [110], eine Waschmaschinensteuerung [177] usw. [179, 190].

Beim Entwurf von Fuzzy-Reglern wird wie folgt vorgegangen:

Schritt 1: Man bestimmt die interessierenden linguistischen Variablen x

, y

die die Eingangs- und Ausgangsgr

oßen des Fuzzy-Reglers bilden.

Schritt 2: Jeder linguistischen Variablen x

, y

wird eine Reihe von linguisti-

schen Werten LW

i,j

zugeordnet.

5.3. Fuzzy-Control 279

Fuzzy-Regler

Prozess

Bild 5.34: Regelkreis mit Fuzzy-Regler.

Schritt 3: Zu den LW

i,j

werden Zugeh

origkeitsfunktionen μ

i,j

gew

ahlt.

Schritt 4: Die Regeln werden ermittelt.

Dabei imitiert man mittels des Fuzzy-Reglers in den meisten F

allen einen

Menschen, der die Regelung vornimmt oder vornehmen k

onnte. Dies kann

z. B. der Prozessbediener eines chemischen oder biotechnologischen Prozesses

oderderFahrereinerU-Bahnsein.

Mit obigem Entwurf kann der Regler oder eine Steuerung nur in seltenen

allen auf Anhieb so ausgelegt werden, dass er bereits das gew

unschte Verhal-

ten zeigt. Denn der erste Entwurf wird die menschliche Verhaltensweise nicht

genau genug nachzeichnen k

onnen. Folglich f

uhrt man den Entwurf solange

erneut mit ver

anderten Parametern und Regeln durch, bis sich ein zufrieden-

stellendes Verhalten ergibt. In Bild 5.35 ist diese Vorgehensweise dargestellt.

Erstellung des

Fuzzy-Reglers

Erprobung in

Simulation oder Praxis

Verbesserung von

Regeln, Zugeh

orig-

keitsfunktionen etc.

Gew

unschtes

Verhalten erreicht?

Ende

Nein

Bild 5.35: Vorgehensweise bei der Auslegung eines Fuzzy-Reglers.

280 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

Der Entwurf basiert auf Versuch und Irrtum und wird mehrfaches Optimieren

erfordern.

Es ist zu beachten, dass der Fuzzy-Regler ein rein statischer Kennfeldregler

ist. Er ist nichtlinear, aber ohne Dynamik. Seine Nichtlinearit

at zieht die

Problematik nach sich, dass die Stabilit

at des Regelkreises nicht oder nur

mit gr

oßerem Aufwand nachweisbar ist. Dies ist einer der Gr

unde daf

ur, dass

Fuzzy-Regler haupts

achlich in F

allen eingesetzt werden, bei denen man mit

klassischen Reglern und der mit ihnen einhergehenden Stabilit

atssicherung

des Regelkreises keine befriedigenden Ergebnisse erzielt.

5.3.6 Beispiel Abstandsregelung f

ur Automobile

Als Anwendungsfall f

ur einen Fuzzy-Regler soll eine Abstandsregelung f

ur Au-

tomobile betrachtet werden, wie sie in

ahnlicher Form in [61, 73] beschrieben

wird.Zielistes,dieGeschwindigkeitv bzw. Beschleunigung a eines Automo-

bils so zu bestimmen, dass der Abstand zu einem vorausfahrenden Fahrzeug

dem gesetzlich vorgeschriebenen Wert (halber Tacho), d. h.

soll

ist

mit x

soll

in Metern und v

ist

in Kilometern pro Stunde, entspricht. Bild 5.36

illustriert die Situation.

Folgende Gr

oßen sind f

ur die Abstandsregelung relevant:

leit

: Geschwindigkeit des vorausfahrenden Fahrzeuges,

ist

: Geschwindigkeit des geregelten Fahrzeuges,

rel

= v

leit

− v

ist

: Relativgeschwindigkeit,

rel

: Abstand,

Δx

rel

= x

rel

− x

soll

: Abstandsabweichung,

soll

: Wunschbeschleunigung des geregelten Fahrzeuges,

ist

: Beschleunigung des geregelten Fahrzeuges.

Als Messwerte stehen f

ur die Regelung neben v

ist

auch v

rel

und x

rel

zur

Verf

ugung. Gemessen werden Letztere mittels Radarsensor oder Laser. Die

Regelstrecke ist eine Beschleunigungs-Weg-Strecke, d. h., sie ist durch einen

rel

ist

leit

Bild 5.36: Abstandsregelung.

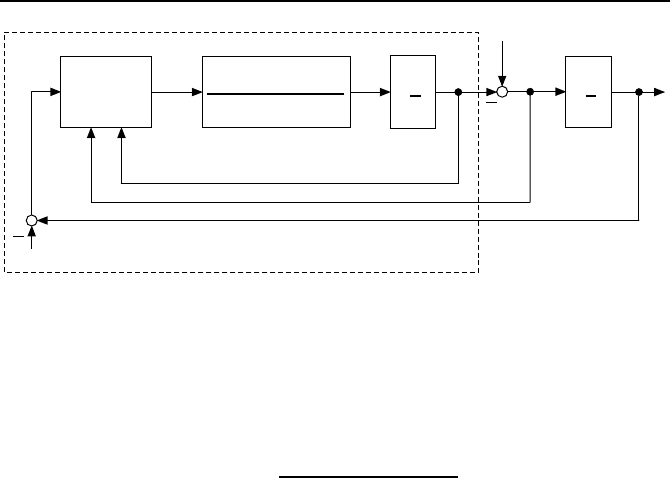
5.3. Fuzzy-Control 281

geregeltes Fahrzeug

Beschleunigungs-

regelkreis

Fuzzy-

Abstands-

regelung

soll

Δx

rel

soll

ist

leit

rel

(1+T

s)(1+T

Bild 5.37: Abstandsregelkreis.

Doppelintegrierer zu beschreiben. Hinzu kommen noch zwei Verz

ogerungs-

glieder erster Ordnung f

ur einen unterlagerten Beschleunigungsregelkreis. Die

Ubertragungsfunktion des Regelkreises lautet also

G(s)=

(1 + T

s)(1 + T

mit T

=0.074 s und T

=0.14 s. Es ergibt sich dann der in Bild 5.37 darge-

stellte Regelkreis.

Es liegt nahe, f

ur den Abstandsregler die Verhaltensweise des Menschen

mittels eines Fuzzy-Reglers nachzuahmen. Auch der Mensch benutzt Δx

rel

und v

ist

als Orientierungsgr

oßen, um die Beschleunigung a

soll

seines Fahr-

zeuges zu verringern oder zu erh

ohen. Prinzipiell k

onnte solch eine Abstands-

regelung auch durch einen linearen Regler realisiert werden. Jedoch garantiert

ein linearer Regler kein ausreichend sicheres Fahrverhalten bei einscherenden

Fahrzeugen oder langsamen Fahrzeugen, die nach Kurven auftauchen. Der

Fuzzy-Abstandsregler leistet dies und hat dann die Form, wie sie in Bild 5.37

dargestellt ist.

Im ersten Entwurfsschritt legt man linguistische Werte und die Zugeh

orig-

keitsfunktionen von Δx

rel

, v

ist

, v

rel

und a

soll

fest. F

ur die Eingangsgr

oßen erge-

ben sich die Zugeh

origkeitsfunktionen gem

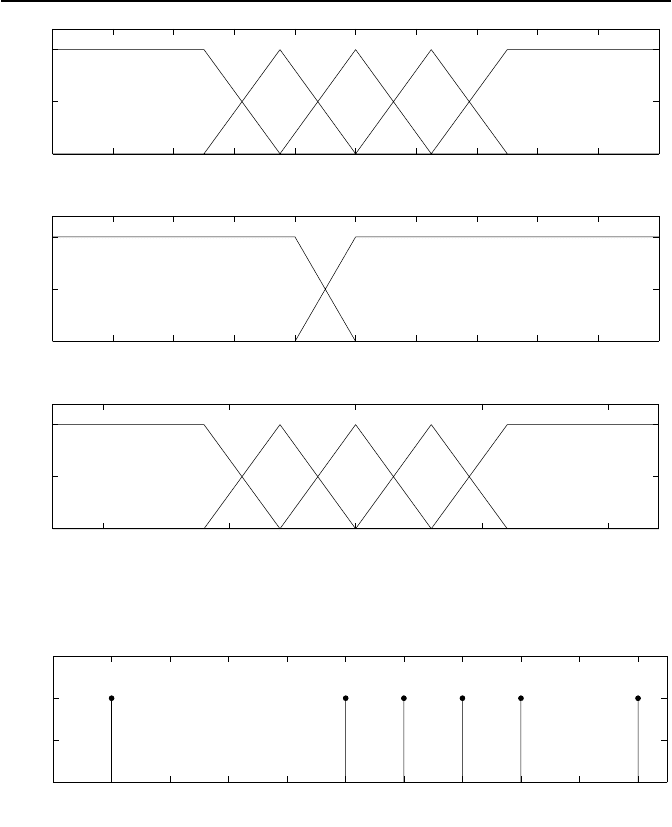
aß Bild 5.38, f

ur die Ausgangsgr

oße

die Zugeh

origkeitsfunktionen gem

aß Bild 5.39.

Im n

achsten Schritt werden die Regeln festgelegt, wobei man die Matrix-

form in Tabelle 5.6 benutzt. Dabei sind die linguistischen Werte geeignet ab-

gek

urzt. Die Matrixeintr

age geben die Beschleunigung a

soll

an.

Als Operatoren nutzt man f

ur Aggregation und Implikation den min-

Operator und f

ur die Akkumulation den max-Operator. F

ur die Defuzziﬁzie-

rung verwenden wir die COS-Methode. Obige Festlegungen haben den Vorteil,

dass eine kosteng

unstige und einfache Realisierung, z. B. mit einem Festkom-

maprozessor, m

oglich ist. Insbesondere bei der Verwendung von anderen Zu-

geh

origkeitsfunktionen als Singletons und der Fl

achenschwerpunktsmethode

282 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

Diﬀerenz Δx

rel

von Abstand und Sollabstand in m

Istgeschwindigkeit v

ist

in m s

−1

Relativgeschwindigkeit v

rel

in m s

−1

Zugeh

origkeit Zugeh

origkeit

zk ezk OK ezg zg

langsam schnell

lelgses s

0.5

-25 -20 -15

-10

-5

30 35 40

Bild 5.38: Zugeh

origkeitsfunktionen der Eingangsgr

oßen.

1.5

0.5

-7

-6

-5

-4

-3

-2 -1

gsv v ev n eb sb

Sollbeschleunigung a

soll

in m s

−2

Zugeh

origkeit

Bild 5.39: Zugeh

origkeitsfunktionen der Ausgangsgr

oße.

COA als Defuzziﬁzierungsmethode w

urde die Auswertung wesentlich komple-

xer und auch kostenintensiver. Im hier vorliegenden Fall erg

aben sich außer-

dem keine Vorteile, denn das Regelverhalten ist bei beiden Varianten sehr

ahnlich.

Insgesamt erh

alt man 50 Regeln. Dabei bildet der Fuzzy-Regler einen

Kennfeldregler, dessen Kennfeld vierdimensional ist. F

ur die Fahrzeugge-

schwindigkeiten v

ist

=10ms

−1

,d.h.f

ur langsam, und v

ist

=30ms

−1

,d.h.

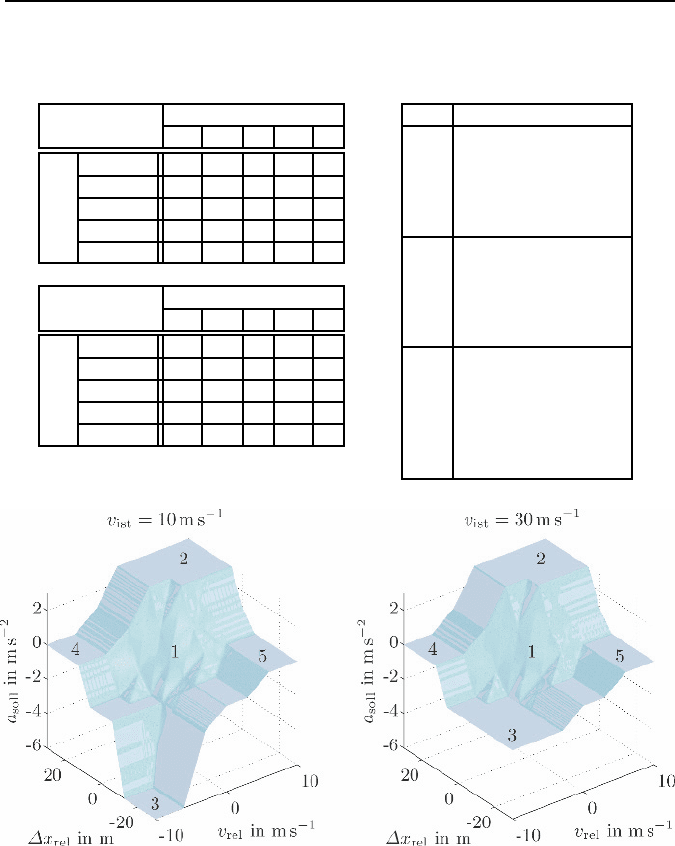
5.3. Fuzzy-Control 283

Tabelle 5.6: Fuzzy-Regeln der Abstandsregelung mit den Eingangsgr

oßen v

ist

, Δx

rel

und v

rel

sowie der Ausgangsgr

oße a

soll

Δx

rel

ist

=langsam

zk ezk ok ezg zg

l gsv v v v n

el v v v ev eb

rel

gs ev ev n eb sb

es ev ev eb sb sb

s n n eb sb sb

Δx

rel

ist

=schnell

zk ezk ok ezg zg

l v v v v n

el v v v ev eb

rel

gs ev ev n eb sb

es ev ev eb sb sb

s n n eb sb sb

Abk. Bedeutung

l langsamer

el etwas langsamer

gs gleich schnell

es etwas schneller

s schneller

zk zu klein

ezk etwas zu klein

ok ok

ezg etwas zu groß

zg zu groß

gsv ganz stark verz

ogern

v verz

ogern

ev etwas verz

ogern

n null

eb etwas beschleunigen

sb stark beschleunigen

Bild 5.40: Kennfelder des Fuzzy-Abstandsreglers bei den Geschwindigkeiten v

ist

10 m s

−1

und v

ist

=30ms

−1

des geregelten Fahrzeuges.

ur schnell, sind die entsprechenden Teil-Kennfelder in Bild 5.40 graﬁsch dar-

stellbar. F

unf wesentliche Bereiche sind in diesem nichtlinearen Reglerkenn-

feld zu erkennen. Im Bereich 1 entspricht das Reglerverhalten ann

ahernd ei-

nem linearen Regler. Dieser Bereich kennzeichnet den station

aren Zustand mit

rel

≈ 0ms

−1

und korrektem Abstand x

rel

≈ x

soll

,d.h.Δx

rel

≈ 0. Im Bereich

2 kann der Wagen mit maximaler Beschleunigung aufholen, da der Abstand

284 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

groß ist und sich der vorausfahrende Wagen entfernt. Im Bereich 3 muss ma-

ximal gebremst werden, denn der Abstand ist viel zu gering. Im Bereich 4

ahert man sich mit geringer Relativgeschwindigkeit aus großem Abstand.

Hier wird die Geschwindigkeit nicht ver

andert. Also gilt a

soll

=0ms

−2

,bis

der Wagen aufgeholt hat. Im Bereich 5 f

ahrt der vorausfahrende Wagen bei

zu geringem Abstand davon. Daher wird nicht beschleunigt oder gebremst,

bis der richtige Abstand erreicht ist.

Aus den Kennfeldern ist auch erkennbar, dass nur in den relativ kleinen

Bereichen 4 und 5 weder beschleunigt noch gebremst wird. Folglich wird bei

einer Abstandsregelung bei dichtem Verkehr st

andig beschleunigt oder ge-

bremst. In der Praxis ist eine Abstandsregelung mit einem Tempomat kombi-

niert, so dass bei geringer Verkehrsdichte die Geschwindigkeitsregelung durch

den Tempomat ausgef

uhrt wird. Die Brems- und Beschleunigungsvorg

ange

entfallen dann.

Zeit t in s

Beschleunigung in m s

−2

Geschwindigkeit in m s

−1

Abstand in m

Sollabstand

Istabstand

vorderer PKW

geregelter PKW

ﬂießender Verkehr

Stop-and-goStop-and-go

-2

-4

100

150

200

250

300

350

400

450

500

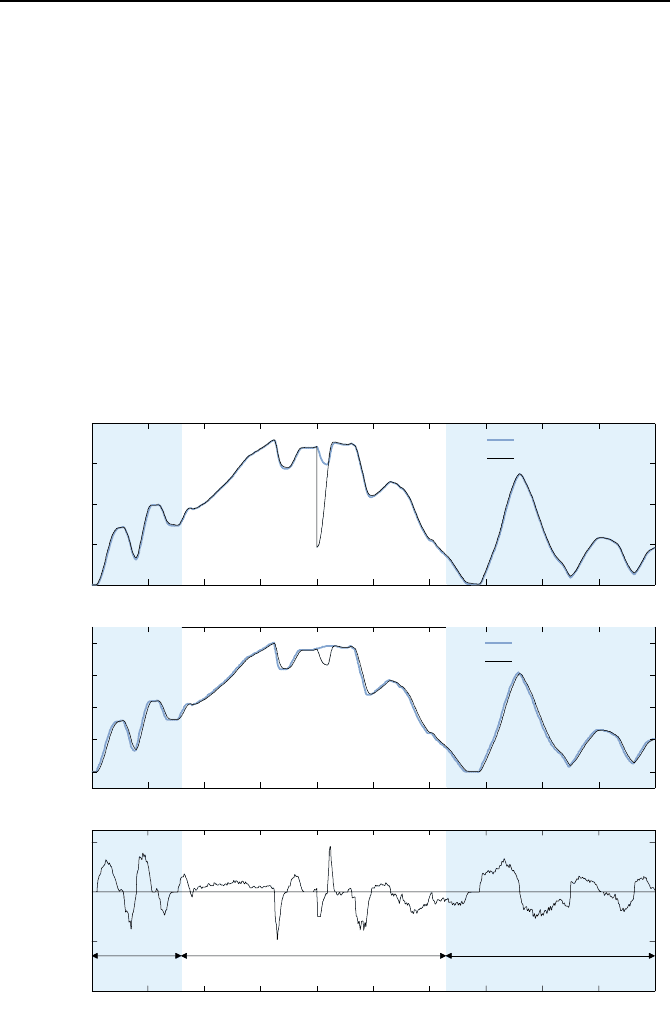
Bild 5.41: Messungen auf einer simulierten Autobahnfahrt.

5.3. Fuzzy-Control 285

In Bild 5.41 sind die Beschleunigung a

soll

, die Geschwindigkeiten v

ist

und v

leit

und der Abstand x

rel

sowie der Sollabstand x

soll

zweier Fahrzeuge

ahrend einer Fahrt auf der Autobahn von ca. 8 min bei sehr dichtem Verkehr

dargestellt. Deutlich erkennbar ist das in allen Bereichen gute Regelverhalten.

Das nachfolgende, geregelte Fahrzeug h

alt den gesetzlich vorgeschriebenen

Abstand fast exakt ein. Das gilt auch f

ur den Vorfall bei t = 200 s, als ein

Fahrzeug mit einem zugeh

origen Abstand von ca 18.5 m bei einer Geschwin-

digkeit von 38 m s

−1

≈ 137 km h

−1

vor dem geregelten Fahrzeug einschert. Die

Regelung stellt danach innerhalb von ca. 10 s wieder den korrekten Abstand

her.

Beachtenswert ist auch der Zeitraum zwischen den Sekunden 320 und 350,

in dem der Verkehr v

ollig zum Erliegen kommt. Es gelingt der Regelung auch

hier, einen sicheren Abstand einzuhalten, der beim Stillstand der Fahrzeuge

allerdings nur noch im Zentimeterbereich liegt. F

ur den praktischen Einsatz

wird man den Sollabstand durch einen einzuhaltenden Wert von z. B. x

min

2 m nach unten begrenzen. Man ersetzt dann die Gleichung x

soll

=0.5v

ist

durch x

soll

=0.5v

ist

+ x

min