J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.


246 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
werden. Oder die Stabilit
¨
at wird nur simulatorisch f
¨
ur ausgew
¨
ahlte F
¨
alle un-
tersucht.
5.1.6 Beispiel Eindampfanlage
Wir betrachten als Beispiel eine Eindampfanlage, wie sie z. B. zur Herstel-
lung von Sirup in Zuckerfabriken verwendet wird [136, 188]. Wie in Bild
5.10 dargestellt, besteht die Anlage aus einem Verdampfer, einem Abschei-
der und einem Kondensator. Der Eingangsstoff, Rohsaft aus Zuckerr
¨
uben,
wird dem Verdampfer zugef
¨
uhrt, der als W
¨
armetauscher ausgelegt ist. Der
W
¨
armetauscher wird mit Dampf des Druckes P
D
beheizt. Der im Verdampfer
unter dem Druck P
V
erhitzte Ausgangsstoff verl
¨
asst diesen als Gemisch aus
Dampf und Fl
¨
ussigkeit und gelangt dann in den Abscheider. In ihm wird der
Dampf abgetrennt und in einen Kondensator geleitet. Gek
¨
uhlt durch Was-
ser, das mit der Zuflussrate q
C
in den Kondensator str
¨
omt, kondensiert der
Dampf und wird aus der Anlage abgef
¨
uhrt. Das im Abscheider gesammelte
Konzentrat hat dort den F
¨
ullstand h. Ein Teil dieses Konzentrates mit der
Verdampfer
Abscheider Kondensator
verdampfter
Stoff
Dampf
Eingangs-
stoff
Produkt mit u
2
= q
P
und x
2
= K
P
Konzentrat
Kondensat
x
1
h
x
3
P
V
u
1
P
D
u
3
q
C
Bild 5.10: Eindampfanlage mit Verdampfer, Abscheider und Kondensator.

5.1. Modellbasierte pr
¨
adiktive Regelung 247
Konzentration K
P
wird dem Prozess nun mit der Volumenrate q
P
als Produkt
entnommen. Der weitaus gr
¨
oßere Teil wird jedoch, mit dem Eingangsstoff ver-
mischt, dem Verdampfer erneut zugef
¨
uhrt.
Das System l
¨
asst sich durch ein nichtlineares Modell dritter Ordnung be-
schreiben. Dabei sind x
1
= h, x
2
= K
P
und x
3
= P
V
die Zustandsvariablen
und u
1
= P
D
, u
2
= q
P
und u
3
= q
C
die Stellgr
¨
oßen des Systems. Wir messen
x
1
in m, x
2
in %, x
3
und u
1
in kPa und u
2
sowie u
3
in kg min
−1
.DasModell
hat die folgende Auspr
¨
agung:
˙x
1
= a
1
x
3
+ a
2
x
2
− b
1
u
1
− b
2
u
2
− k
1
,
˙x
2
= −a
3
x
2
u
2
+ k
2
,
˙x
3
= −a
4
x
3
− a
5
x
2
+ b
3
u
1
−
a
6
x
3
+ b
4
b
5
u
3
+ k
3
u
3
+ k
4
.
(5.25)
Die Parameter des Systems sind
a
1
=0.00751,b
1
=0.00192,k
1
=0.01061,
a
2
=0.00418,b
2
=0.05,k
2
=2.5,
a
3
=0.05,b
3
=0.00959,k
3
=6.84,
a
4
=0.03755,b
4
=0.1866,k
4
=2.5531,
a
5
=0.02091,b
5
=0.14,
a
6
=0.00315.
Die Zustandsvariablen sind auch gleichzeitig die Ausgangsvariablen y
1
= x
1
,
y
2
= x
2
und y
3
= x
3
des Prozesses. Sowohl die Zustandsvariablen als auch die
Stellgr
¨
oßen unterliegen Beschr
¨
ankungen der Form
0m≤ x
1
≤ 2m,
0%≤ x
2
≤ 50 %,
0kPa≤ x
3
≤ 100 kPa,
0kPa≤ u
1
≤ 400 kPa,
0kgmin
−1
≤ u
2
≤ 4kgmin
−1
,
0kgmin
−1
≤ u
3
≤ 400 kg min
−1
.
(5.26)
Die Ruhelage x
R
des Systems (5.25) kann
¨
uber die Stellgr
¨
oßenwerte
u
1R
=
1
b
1
a
1
x
3R
+ a
2
x
2R
− k
1
−
b
2
k
2
a
3
x
2R
,
u
2R
=
k
2
a
3
x
2R
,
u
3R
=
k
3
(−a
4
x
3R
− a
5
x
2R
+ k
4
+ b
3
u
1R
)
(a
6
+ a
4
b
5
)x
3R
+ a
5
b
5
x
2R
− b
5
k
4
+ b
4
− b
3
b
5
u
1R
vorgegeben werden. Im Folgenden w
¨
ahlen wir

248 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
x
R
= [1 15 70]
T
,
woraus sich
u
R
=
214.13 3.33 65.40
T
ergibt.
Um eine modellpr
¨
adiktive Regelung verwenden zu k
¨
onnen, legen wir den
Regler zeitdiskret aus. Dabei betr
¨
agt die Dauer eines Stellgr
¨
oßenschrittes
T =1min.
Wir w
¨
ahlen f
¨
ur den Pr
¨
adiktions- und den Stellhorizont n
p
= n
c
= 5 und
als G
¨
utefunktion
J(k)=
k+4
i=k
(x(i) − x
R
)
T
Q (x(i) − x
R
)+r (u(i) − u
R
)
T
(u(i) − u
R
) .
Dabei ist
Q =
⎡
⎣
100 0 0
01 0
0010
⎤
⎦
und r =0.1. Die G
¨
utefunktion mit den Nebenbedingungen (5.26) wandeln wir
mittels einer Barrierefunktion so um, dass die nicht beschr
¨
ankte G
¨
utefunktion
˜
J(k)=
J(k), wenn alle x(i), u(i),i=1,...,4, die Gl.(5.26) erf
¨
ullen,
∞, wenn ein x(i), u(i),i=1,...,4, die Gl.(5.26) nicht erf
¨
ullt,
zu minimieren ist. Das G
¨
utemaß
˜
J l
¨
asst sich aufgrund der kartesischen Begren-
zungen durch Gl. (5.26) effizient mit dem Optimierungsverfahren von Hooke
und Jeeves [74, 164] minimieren. Die dabei n
¨
otige numerische L
¨
osung der Sys-
temgleichung (5.25) f
¨
uhren wir mittels des Verfahrens von Euler-Cauchy mit
einer Schrittweite von 2.4 s aus.
Eine Stabilit
¨
atsuntersuchung f
¨
ur diese NMPR w
¨
are kompliziert und sehr
aufwendig. Daher verzichten wir auf sie. Theoretisch ist das unbefriedigend,
in der Praxis aber, wie erw
¨
ahnt, h
¨
aufig anzutreffen.
Wir betrachten den auszuregelnden Anfangszustand
x(0) =
⎡
⎣
1
25
50
⎤
⎦
.
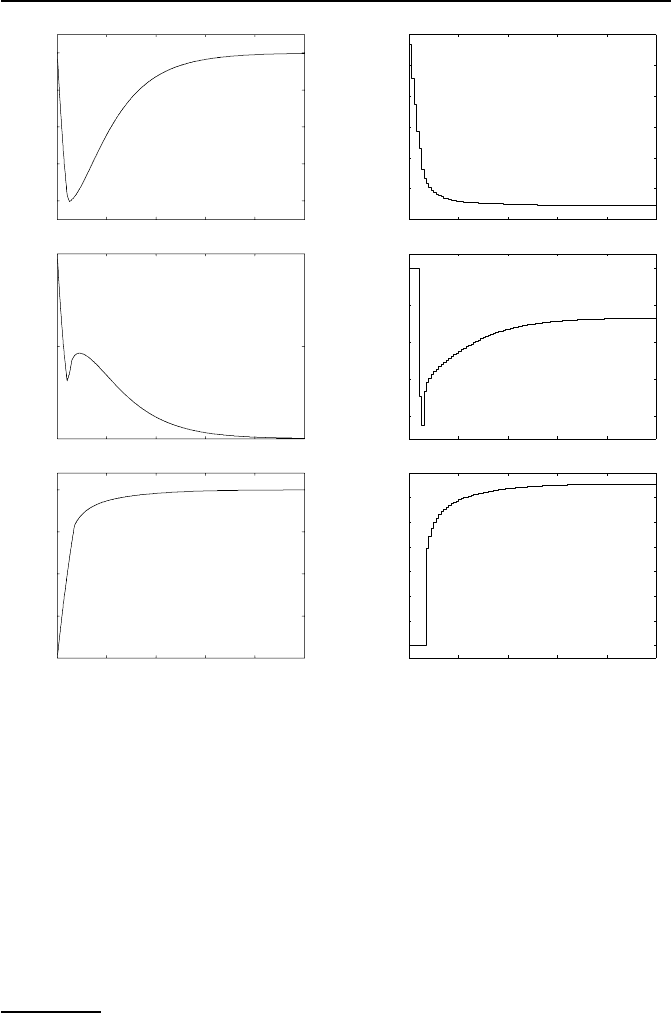
Die Ausregelverl
¨
aufe und Stellgr
¨
oßenverl
¨
aufe, die die MPR bewirkt, zeigt Bild
5.11. Neben der guten Ausregelung erkennt man des Weiteren, dass alle Be-
schr
¨
ankungen (5.26) f
¨
ur x
1
, x
2
, x
3
, u
1
, u
2
und u
3
eingehalten werden. Insbe-
sondere gilt das f
¨
ur die Durchfl
¨
usse u
2
und u
3
, die jeweils 4 min und 7 min
auf ihrem maximalen und minimalen Wert von u
2
=4kgmin
−1
und u
3
=0
kg min
−1
gehalten werden.
5.2. Strukturvariable Regelungen mit Gleitzustand 249
1
0.8
0.6
0.4
0.2
25
20
20
15
70
70
65
60
60
55
50
50
270
260
250
240
230
220
210
4
3.5
3
2.5
2
40
30
10
0
0
0
0
0
0
0
20
20
20
20
20
20
40
40
40
40
40
40
60
60
60
60
60
60
80
80
80
80
80
80
100
100
100
100
100
100
Abtastschritt k,Zeitt in min
Abtastschritt k,Zeitt in min
Pegelstand x
1
in m
Konzentration x
2
in %
Druck x
3
in kPa
Druck u
1
in kPa
Durchfluss u
2
in kg min
−1
Durchfluss u
3
in kg min
−1
Bild 5.11: Eindampfanlage mit pr
¨
adiktiver Regelung mit Abtastzeit T =1min.
5.2 Strukturvariable Regelungen mit Gleitzustand
5.2.1 Funktionsweise und Eigenschaften
Gleitzustandsregler
[1]
,auchSliding-mode-Regler genannt, schalten zwischen
zwei Regelgesetzen in Abh
¨
angigkeit vom Zustandsvektor hin und her. Da-
bei treten Gleitzust
¨
ande auf, die als Vorteil die Robustheit der Regelung ge-
gen
¨
uber Parameterschwankungen der Regelstrecke aufweisen. Nachteilig ist
[1]
In der englischsprachigen Literatur werden Gleitzustandsregler meistens als
”
variable-structure-controls“ bezeichnet. Strukturvariable Regelungen umfassen
allerdings, wie in Kapitel 3.3 beschrieben, eine viel gr
¨
oßere Klasse von Regelun-
gen als nur Gleitzustandsregler.

250 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
das hochfrequente Schalten des Stellgliedes. Dies f
¨
uhrt h
¨
aufig zu vorzeitigem
Verschleiß.
Urspr
¨
unglich zur Regelung linearer Systeme gedacht, wurden sp
¨
ater Er-
weiterungen f
¨
ur nichtlineare Regelstrecken vorgenommen. Wir betrachten im
Weiteren zuerst lineare Regelstrecken, da anhand dieser Systeme die wesentli-
chen Grundlagen der Gleitzustandsregelung erfassbar sind. Darauf aufbauend
werden im Abschnitt 5.2.6 dann auch nichtlineare Regelstrecken in die Be-
trachtungen einbezogen.
Um das Prinzip der Gleitzustandsregelung zu erl
¨
autern, wird zu Beginn
als einfaches Beispiel die Regelstrecke
˙x
1
= x
2
,
˙x
2
= a · u, a > 0,
(5.27)
mit dem Regler
u = −u
max
sgn (x
2
+ mx
1
) (5.28)
betrachtet. Hierbei sind u
max
und m reelle Konstanten des Reglers. Betrachtet
man obigen Regelkreis in der Zustandsebene, so l
¨
asst sich feststellen, dass das
Regelgesetz die Zustandsebene durch die Schaltgerade
x
2
= −mx
1
(5.29)
in zwei Bereiche teilt. Unterhalb der Schaltgeraden gilt
u = u
max
,
oberhalb
u = −u
max
.
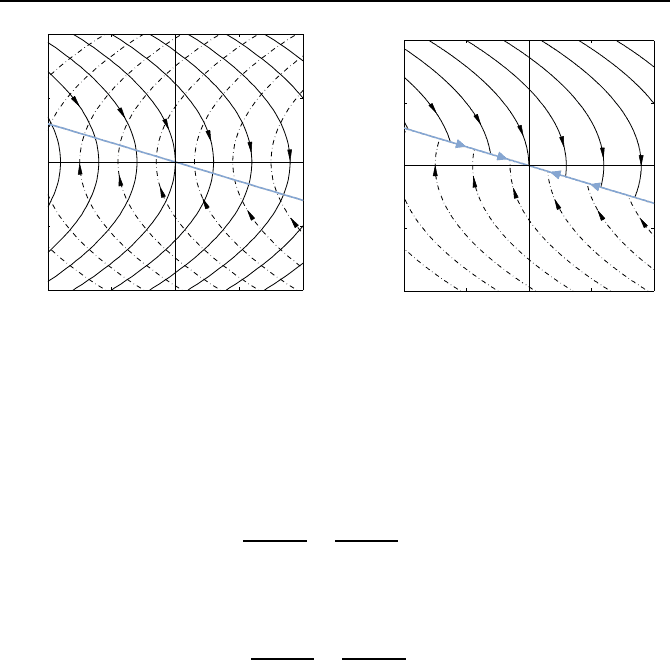
Bild 5.12 zeigt beispielhaft die Schaltgerade (5.29) und die Trajektorien der
Regelstrecke f
¨
ur die Stellgr
¨
oßen u = ±u
max
, die der Regler (5.28) ausgeben
kann.
F
¨
ur die Trajektorien x(t)=[x
1
(t) x
2
(t)]
T
des Systems ergeben sich Para-
bel
¨
aste. Um sie zu bestimmen, ermittelt man f
¨
ur u = u
max
die L
¨
osungen der
Differenzialgleichungen (5.27) zu
x
2
= x
2
(0) +
t
0
au
max
dτ = au
max
t + x
2
(0), (5.30)
x
1
= x
1
(0) +
t
0
x
2
dτ =
1
2
au
max
t
2
+ x
2
(0)t + x
1
(0). (5.31)
Aus Gl. (5.30) resultiert
t =
x
2
− x
2
(0)
au
max
.
5.2. Strukturvariable Regelungen mit Gleitzustand 251
x
1
x
2
2
1
0
-2
-1
0
-5 5
10
-10
Bild 5.12: Systemtrajektorien f
¨
ur
u = −u
max
(durchgezogen) und f
¨
ur
u = u
max
(strichpunktiert) sowie die
blau dargestellte Schaltgerade.
x
1
x
2
2
1
0
-2
-1
0
-5 5
10
-10
Bild 5.13: Trajektorien des Regelkrei-
ses mit blau dargestelltem Gleitzu-
stand. Oberhalb der Schaltgeraden ist
u = −u
max
, unterhalb gilt u = u
max
.
Eingesetzt in Gl. (5.31) ergibt sich
x
1
=
x
2
2
2au
max
−
x
2
(0)
2
2au
max
+ x
1
(0).
Die Parabel
¨
aste sind also symmetrisch zur x
2
-Achse, d. h., sie haben ihre
Scheitelpunkte auf der x
2
-Achse. F
¨
ur den Fall u = −u
max
ergibt sich analog
x
1
= −
x
2
2
2au
max
+
x
2
(0)
2
2au
max
+ x
1
(0).
Das Regelgesetz (5.28) bewirkt, dass die Trajektorien von beiden Seiten
auf die Schaltgerade x
2
= −mx
1
zulaufen. Bild 5.13 illustriert dies f
¨
ur den
Wert m =0.06. Dieser Trajektorienverlauf verursacht nach dem Auftreffen
auf die Schaltgerade ein st
¨
andiges Hin- und Herschalten zwischen −u
max
und
u
max
. Dabei gleitet die Trajektorie x(t) auf der Schaltgeraden in die Ruhelage
x
R
= 0. Beschrieben wird die Dynamik des Gleitens durch die Schaltgerade
(5.29) selbst, die
¨
uber
x
2
=˙x
1
= −mx
1
(5.32)
eine Dynamik vorgibt. Theoretisch wechselt die Trajektorie dabei unendlich
schnell mit infinitesimal kleiner Auslenkung von einer Seite der Schaltgeraden
zur anderen.
Dabei tritt ein Schalten zwischen −u
max
und u
max
mit unendlich hoher
Frequenz auf, das als Rattern bezeichnet wird. In der Praxis ist die Schaltfre-
quenz nat
¨
urlich nicht unendlich groß, sondern h
¨
angt von der Geschwindigkeit
des Stellglieds ab. Das Rattern ist, wie schon erw
¨
ahnt, ein eklatanter Nach-
teil der Gleitzustandsregelung, denn mechanische Stellglieder verschleißen da-
durch schnell.

252 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
Die Regelung hat aber auch einen Vorteil, denn im Gleitzustand ist die
Regelung robust gegen Variationen der Regelstrecke. D. h., die Regelkreisdy-
namik ist immer dieselbe, auch wenn sich die Regelstrecke
¨
andert. So liegt
beim vorangegangenen Beispiel im Gleitzustand mit Gl. (5.32) die Dynamik
˙x
1
= −mx
1
,
˙x
2
=¨x
1
= −m ˙x
1
= m
2
x
1
= −mx
2
vor. Diese Dynamik ist also unabh
¨
angig vom Parameter a der Regelstrecke
(5.27).
5.2.2 Entwurf f
¨
ur lineare Regelstrecken
Der Ausregelvorgang einer Gleitzustandsregelung kann in drei Bereiche un-
terteilt werden:
(1) die Eintreffphase, in der die Trajektorien auf die Schaltgerade bzw. Schalt-
hyperebene zulaufen und sie in endlicher Zeit erreichen,
(2) die Gleitzustandsphase, in der die Trajektorie auf der Schalthyperebene
in die Ruhelage gleitet und
(3) die Ruhelage x
R
= 0, in der das System stabil verbleibt.
F
¨
ur eine global stabile Ruhelage x
R
= 0 muss sichergestellt sein, dass alle
Trajektorien des Systems in endlicher Zeit auf die Schaltebene und dann im
Gleitzustand in die Ruhelage x
R
= 0 laufen.
Wir betrachten, wie erw
¨
ahnt, lineare Regelstrecken
˙x = Ax + bu
mit einer Schaltfl
¨
ache
s(x)=0
und dem Regelgesetz
u(x)=
u
+
(x)f
¨
ur s(x) > 0,
u
−
(x)f
¨
ur s(x) < 0.
Die Stellgr
¨
oße u ist hierbei nicht f
¨
ur s(x) = 0 definiert. In den meisten F
¨
allen
verwendet man als Schaltfunktion
s(x)=r
T
x,
also eine Schaltfl
¨
ache r
T
x =0.
Als erstes soll die Erreichbarkeit der Schaltfl
¨
ache f
¨
ur alle Trajektorien des
Zustandsraumes sichergestellt werden. Eine notwendige Bedingung hierf
¨
ur ist,
dass die Trajektorien des Regelkreises von beiden Seiten auf die Schaltfl
¨
ache
zulaufen, so wie es Bild 5.13 zeigt. D. h., es muss

5.2. Strukturvariable Regelungen mit Gleitzustand 253
˙s<0f
¨
ur s(x) > 0
und
˙s>0f
¨
ur s(x) < 0
gelten. Fasst man beide Bedingungen zusammen, so erh
¨
alt man
s ˙s<0
als Bedingung f
¨
ur einen Gleitzustand. Hierbei gilt
˙s =grad
T
s(x) · ˙x
und f
¨
ur den Fall s(x)=r
T
x ergibt sich dann ˙s = r
T
˙x. Leider sichert die
Bedingung s ˙s<0nichtf
¨
ur jeden denkbaren Fall, dass die Trajektorien die
Schaltebene s(x) = 0 in endlicher Zeit erreichen. Die Bedingung ist also not-
wendig, aber nicht hinreichend f
¨
ur eine funktionsf
¨
ahige Gleitzustandsregelung.
Es gibt verschiedene Ans
¨
atze, die Erreichbarkeit der Schaltfl
¨
ache f
¨
ur alle
Trajektorien in endlicher Zeit zu gew
¨
ahrleisten. Ein sehr verbreiteter Ansatz
ist der von Gao und Hung [58]. Hier wird die Abnahme ˙s(x) der Schaltfunktion
entlang der Trajektorien x(t) vorgegeben. Es gilt
˙s(x)=−q sgn(s(x)) − ks(x) (5.33)
mit positiven Konstanten q und k. Offensichtlich erf
¨
ullt im Falle der Gl. (5.33)
die Schaltfl
¨
ache s die notwendige Bedingung
s ˙s = −q|s|−k · s
2
< 0.
Da s aufgrund der Wahl von ˙s in Gl. (5.33) auch f
¨
ur sehr kleine Werte von
|s| eine Abnahmerate ˙s<− q bzw. eine Zunahmerate von ˙s>qaufweist,
erreichen die Trajektorien x(t) die Schaltfl
¨
ache auch in endlicher Zeit.
Ber
¨
ucksichtigt man, dass
˙s(x) = grad
T
s(x) · ˙x =grad
T
s(x) · (Ax + bu)
ist, so erh
¨
alt man aus Gl. (5.33) f
¨
ur das Regelgesetz
u(x)=−
grad
T
s(x) · Ax + q sgn(s(x)) + ks(x)
grad
T
s(x) · b
.
F
¨
ur den Fall einer Schalthyperebene als Schaltfl
¨
ache
s(x)=r
T
x =0
ergibt sich
u(x)=−
r
T
Ax + q sgn(r
T
x)+kr
T
x
r
T
b
.

254 Kapitel 5. Regelungen f
¨
ur lineare und nichtlineare Regelstrecken
Durch die frei w
¨
ahlbaren positiven Parameter q und k kann die Regeldynamik
g
¨
unstig beeinflusst werden.
Es sei angemerkt, dass Gleitzustandsregler auch f
¨
ur Systeme mit mehreren
Eingangsgr
¨
oßen, also f
¨
ur
˙x = Ax + Bu,
entworfen werden k
¨
onnen [80, 160, 189].
5.2.3 Dynamik im Gleitzustand
Wenn die Trajektorien x(t) die Schaltfl
¨
ache erreichen und der Gleitzustand
einsetzt, stellt sich die Frage, welche Dynamik der Regelkreis im Gleitzustand
besitzt. Problematisch bei der Betrachtung dieser Frage ist die Unstetigkeit
der Differenzialgleichung
˙x = Ax + bu, u(x)=
u
+
(x)f
¨
ur s(x) > 0,
u
−
(x)f
¨
ur s(x) < 0,
des geschlossenen Regelkreises auf der Schaltfl
¨
ache
s(x)=r
T
x =0.
Die Differenzialgleichung ist offensichtlich auf der Schaltfl
¨
ache nicht defi-
niert, d. h., die Existenz und Eindeutigkeit ihrer L
¨
osung ist dort nicht gesi-
chert. Es existieren verschiedene Verfahren [80] dieses Problem zu l
¨
osen, wie
z. B. die Methode von Filippov [47].
Wir bestimmen die Dynamik des Systems im Gleitzustand hier nach der
folgenden, h
¨
aufig verwendeten Methode. Man transformiert die Regelstrecke
in die Regelungsnormalform
˙x
1
= x
2
,
.
.
.
˙x
n−1
= x
n
,
˙x
n
= −a
0
x
1
− a
1
x
2
− ...− a
n−1
x
n
+ u.
(5.34)
Des Weiteren l
¨
ost man die Gleichung der Schaltfl
¨
ache
r
T
x = r
1
x
1
+ ...+ r
n−1
x
n−1
+ r
n
x
n
= 0 (5.35)
nach x
n
auf, d. h., es gilt
x
n
= −r
1
x
1
− ...− r
n−1
x
n−1
. (5.36)
Der Koeffizient r
n
wurde dabei, r
n
= 0 vorausgesetzt, ohne Einschr
¨
ankung
der Allgemeinheit zu r
n
=1gew
¨
ahlt werden.

5.2. Strukturvariable Regelungen mit Gleitzustand 255
Nun substituiert man in der Regelungsnormalform (5.34) der Strecke die
Zustandsgr
¨
oße x
n
durch Gl. (5.36) und erh
¨
alt das Differenzialgleichungssys-
tem
˙x
1
= x
2
,
.
.
.
˙x
n−2
= x
n−1
,
˙x
n−1
= −r
1
x
1
− ...− r
n−1
x
n−1
,
(5.37)
das die Dynamik des Regelkreises im Gleitzustand beschreibt. Man beachte,
dass die Zustandsgr
¨
oße x
n
in diesem Fall durch die algebraische Gleichung
(5.36) gegeben ist und die Gleichung f
¨
ur ˙x
n
daher entf
¨
allt. Die Differenzial-
gleichungen (5.37) sind nicht mehr von den Parametern a
i
der Regelstrecke
abh
¨
angig. D. h., der Regelkreis (5.37) ist robust gegen
¨
uber Parameterschwan-
kungen der Regelstrecke. Beachtenswert ist dar
¨
uber hinaus, dass sich die Sys-
temordnung um einen Grad auf die Ordnung n −1 verringert hat und die Ko-
effizienten r
i
der Schaltfl
¨
ache (5.35) die Koeffizienten des charakteristischen
Polynoms der linearen Dynamik (5.37) im Falle des Gleitzustandes bilden.
5.2.4 Nachweis der Robustheit
Der wesentliche Vorteil von Sliding-mode-Reglern ist ihre Robustheit ge-
gen
¨
uber Variationen ΔA der Regelstreckenparameter oder
¨
außeren St
¨
orungen
d(t), wenn diese in der Systembeschreibung
˙x =(A + ΔA) x + bu + d
auftauchen. D. h., die Dynamik des geschlossenen Regelkreises h
¨
angt, wie in
Gl. (5.37), im Gleitzustand nur von den Parametern r
i
der Schaltfl
¨
ache s(x)=
r
T
x ab. Die Dynamik ist unabh
¨
angig von ΔA und d.
Wenn die folgenden Bedingungen beide erf
¨
ullt sind [39], stellt sich die oben
beschriebene Robustheit auch wirklich ein:
(1) Es gibt einen Vektor p,sodassΔA = b · p
T
gilt.
(2) Es gibt ein α(t), so dass d(t)=b · α(t) gilt.
Wenn das System beispielsweise in Regelungsnormalform
˙x =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
010··· 0
001··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000··· 1
−a
0
−a
1
−a
2
···−a
n−1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
x +
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0
0
.
.
.
0
1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
u
vorliegt, ist die Bedingung ΔA = b · p
T
offensichtlich erf
¨
ullbar, falls nur die
Koeffizienten a
i
variieren.
