J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

236 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

⎡

⎢

⎣

min,1

min,2

min,r

⎤

⎥

⎦



 

min

≤

⎡

⎢

⎣

(k)

⎤

⎥

⎦



 

y(k)

≤

⎡

⎢

⎣

max,1

max,2

max,r

⎤

⎥

⎦



 

max

unterliegen. Diese lassen sich im Fall der betrachteten linearen Systeme in

Beschr

ankungen der Stellgr

oßen

anderung umrechnen. So gilt f

¯y

min

≤ ¯y(k +1)≤ ¯y

max

mit Gl. (5.9)

¯y

min

≤ g(k)+HΔ¯u(k) ≤ ¯y

max

. (5.15)

Dabei ist ¯y

min



min

···y

min



∈ IR

×1

und f

ur ¯y

max

gilt Entsprechen-

des. Beschr

ankungen von x

sehen

ahnlich aus.

Zusammengefasst lassen sich die Ungleichungen (5.13), (5.14) und (5.15)

in die Form

W Δ¯u(k) ≤ w

mit

W =

⎡

⎢

⎣

−D

−I

−H

⎤

⎥

⎦

und w =

⎡

⎢

⎣

−¯u

min

+ Eu(k − 1)

¯u

max

− Eu(k − 1)

−Δ¯u

min

Δ¯u

max

−¯y

min

+ g(k)

¯y

max

− g(k)

⎤

⎥

⎦

bringen. So erh

alt man ein beschr

anktes Optimierungsproblem der Form

min

Δ¯u(k)

J(Δ¯u(k)) (5.16)

mit den linearen Restriktionen

W · Δ¯u(k) ≤ w. (5.17)

Ist die G

utefunktion durch eine positiv deﬁnite quadratische Form gege-

ben, wie im vorherigen Abschnitt 5.1.2, so k

onnen wir die G

utefunktion (5.11)

verwenden und es liegt ein konvexes quadratisches Optimierungsproblem mit

linearen Restriktionen vor. In diesem Fall besitzt das quadratische Optimie-

rungsproblem (5.16), (5.17) nur ein Minimum. Dieses Minimum kann in der

Regel nicht analytisch, sondern nur numerisch bestimmt werden. Es existieren

allerdings sicher konvergente Standardverfahren der quadratischen Program-

mierung, kurz QP-Verfahren genannt, mit denen das Minimum berechenbar

ist [16, 29, 125]. An dieser Stelle werden die Nachteile der modelbasierten

adiktiven Regelung deutlich: Das Regelgesetz ist nicht explizit angebbar

und seine Auswertung zeitaufwendig.

5.1. Modellbasierte pr

adiktive Regelung 237

5.1.4 Beispiel Entw

asserungssystem

Zur Entw

asserung von Gebieten mit hohem Grundwasserspiegel, wie sie z. B.

in den Niederlanden oder den Everglades der USA vorkommen, werden Kanal-

systeme eingesetzt. Insbesondere bei oder nach starken Regenf

allen muss Was-

ser aus den Entw

asserungskan

alen in benachbarte Fl

usse oder das Meer abge-

pumpt werden. Ansonsten w

urde ein zu hoher Wasserstand Deich, D

orfer und

landwirtschaftliche Fl

achen gef

ahrden. Ein zu niedriger Wasserstand in den

Kan

alen ist allerdings auch problematisch, da hierdurch B

oschungsrutsche ver-

ursacht werden k

onnen. Auch große Schwankungen des Wasserstandes k

onnen

durch Pumpeﬀekte eine Auﬂockerung des Erdreiches in den Kanalwandungen

bewirken, die eine Besch

adigung der Kan

ale nach sich zieht.

Man m

ochte den Wasserstand in den Kan

alen daher weder zu niedrig noch

zu hoch werden lassen. Vielmehr soll sich der Wasserstand innerhalb eines vor-

gegebenen Toleranzbandes bewegen. Zu diesem Zweck setzt man Regelungen

ein, mit denen die aus den Kan

alen abgepumpte Wassermenge festgelegt wird.

Bild 5.5 zeigt den Aufbau eines solchen Entw

asserungssystems. Bei meeres-

nahen Anlagen werden zus

atzlich Speicherkan

ale genutzt, in die das Wasser

bei Hochwasser gepumpt wird. Bei Niedrigwasser ﬂießt das Wasser dann ohne

zus

atzliche Pumpleistung ins Meer ab.

Der Wasserstand h im Kanalsystem ist abh

angig vom Regenwasser, das in

die Kan

ale ﬂießt, und der Menge des abgepumpten Wassers [140] gem

aß der

Beziehung

Bild 5.5: Entw

asserungssystem.

238 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

h(k +1)=h(k)+

(k) − q

(k − k

)). (5.18)

Dabei gibt q

die Wassermenge pro Sekunde an, die aufgrund von Regenf

allen

oder eventuell nachstr

omendem Grundwasser in die Kan

ale ﬂießt, und q

die

abgepumpte Wassermenge pro Sekunde. Die Fl

ache A umfasst die gesamte

ache der Kan

ale, T ist die Zeitspanne in Sekunden zwischen den Zeitpunkten

k und k + 1 und k

ist die Anzahl der Zeitschritte, nach denen die Stellgr

oße

auf den Wasserstand in den Kan

alen wirkt.

Wir betrachten das Entw

asserungssystem des Delﬂandes in den Nieder-

landen. Es weist die Parameterwerte

A = 7300000m

=7.3km

,T= 900 s,k

auf. Wasserstand h und Pumpvolumenstrom q

sind durch

−0.55 m ≤ h ≤−0.30 m

und

−1

≤ q

≤ 75 m

−1

begrenzt. Der Sollwert des Wasserstandes h betr

agt h

soll

= −0.40 m. Der

Wasserstand h der Kan

ale wird bez

uglich des Meeresspiegels angegeben, d. h.,

im Fall h = 0 entspricht der Wasserstand der Kan

ale dem Meeresspiegel. Er

liegt im Delﬂand ungef

ahr einen halben Meter unter dem Meeresspiegel.

Die Zustandsgr

oßen des Systems aus Gl. (5.18) sind die Wasserstandsh

ohe

(k)=h(k) und die um einen Zeitschritt k

=1verz

ogerte Stellgr

oße

(k)=q

(k − 1). Mit obigen Parameterwerten und der aktuellen Stellgr

oße

u(k)=q

(k) erhalten wir aus Gl. (5.18) als Modell

(k +1)=x

(k) − 1.23 · 10

−4

(k)+1.23 ·10

−4

(k),

(k +1)=u(k),

y(k)=x

(k).

Dabei wirkt q

als St

orung.

Ziel einer Regelung ist es nun, St

orungen q

aufgrund starken Nieder-

schlages so auszuregeln, dass der Wasserstand x

unter Einhaltung der Be-

schr

ankungen −0.55 ≤ x

≤−0.30 auf den Sollwert x

= −0.4gef

uhrt wird.

Dabei soll die Stellgr

oße u die Beschr

ankungen 0 ≤ u ≤ 75 nicht verletzen.

Oﬀensichtlich ist obige Regelungsaufgabe gut geeignet f

ur eine modellba-

sierte pr

adiktive Regelung. Denn zum einen steht mit T = 900 s zwischen

zwei Regleraktionen ausreichend Rechenzeit zur Verf

ugung und zum anderen

onnen mit einer modellpr

adiktiven Regelung die Beschr

ankungen von y = x

und u gut ber

ucksichtigt werden.

ur die Auslegung der MPR w

ahlen wir als Pr

adiktionshorizont n

=97

und als Stellhorizont n

=2.DerlangePr

adiktionshorizont von 24 h und

5.1. Modellbasierte pr

adiktive Regelung 239

-0.3

-0.35

-0.4

60 80 100 120 140 160 180 200

r =0

r =0.0001

r =0.000002

Zeit t in Stunden

Abtastschritt k

Wasserstand y in m

Volumenstrom u in m

−1

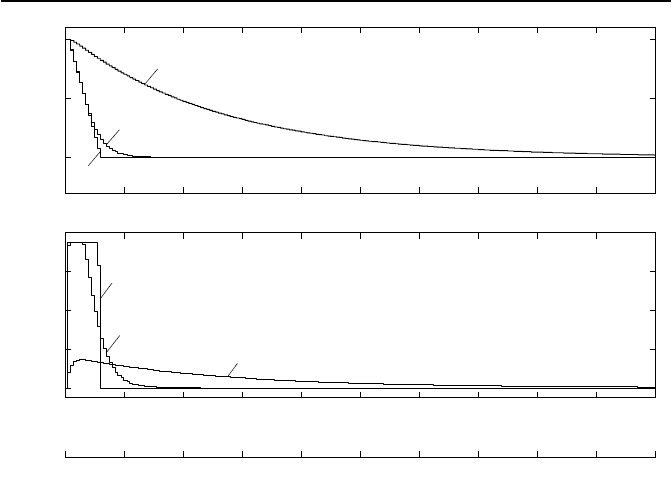
Bild 5.6: Ausgangsverlauf y und Stellgr

oßenverlauf u.

15 min erlaubt u. a. die Einbeziehung einer prognostizierten Regenmenge auf-

grund einer Wettervorhersage. Diese Regenmenge kann

uber q

in der Rege-

lung Ber

ucksichtigung ﬁnden.

ur das G

utemaß w

ahlen wir

J =(¯y(k +1)− ¯y

(k +1))

(¯y(k +1)− ¯y

(k +1))+rΔ¯u

(k)Δ¯u(k),

(5.19)

wobei f

ur den Referenzwert des Wasserstandes y

= h

soll

= −0.4 m gilt. D. h.,

es gilt ¯y

(i)=[−0.4m − 0.4m ··· −0.4m]

ur alle i =0, 1,...

Als praktischen Beispielfall betrachten wir einen erh

ohten Wasserstand

von x

(0) = − 0.3 m nach einer Schlechtwetterfront. Der zweite Anfangswert

ist x

(0) = 0. Bild 5.6 zeigt die Verl

aufe der Stellgr

oße u und des Wasser-

standes y. Dabei sind drei verschiedene Regler verwendet worden, die sich

aus verschiedenen Gewichtungsfaktoren r im G

utemaß (5.19) ergeben. Erwar-

tungsgem

aß ist die MPR f

ur r = 0 am schnellsten und wird f

ur r =0.000002

und r =0.0001 langsamer. Von r h

angt auch die

Anderungsrate der Stellgr

oße

u ab. Spielt ein abruptes Hoch- und Runterfahren des Pumpvolumenstromes u

keine Rolle, so kann r =0gew

ahlt werden. M

ochte man lieber weniger starke

Anderungen Δu im Pumpenvolumenstrom u realisieren, so w

ahlt man einen

oßeren Wert r.Odermanf

uhrt zus

atzlich eine Beschr

ankung von Δu ein.

240 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

100

110

130

190

200

220

100

150

8080

4040

-40-40

-80-80

8080

4040

-40-40

-80-80

Δu

Abtastschritt k =1

Abtastschritt k =5

Abtastschritt k = 10 Abtastschritt k =40

Bild 5.7: Illustration der zu l

osenden Optimierungsprobleme in den Zeitschritten

k =1,k =5,k = 10 und k =40f

ur den Fall r =0.000002. Dargestellt sind die

ohenlinien von J und das zul

assige Optimierungsgebiet (blau). Ein Kreuz markiert

das jeweilige Minimum.

In Bild 5.7 ist die w

ahrend der Regelung zu minimierende G

utefunktion

(5.19) dargestellt. Die H

ohenlinien von J haben die Form von sehr langge-

streckten Ellipsen. Dargestellt ist des Weiteren das zul

assige Gebiet f

ur die

Optimierungsvariablen Δu

und Δu

, wie es sich aus den Beschr

ankungen

ergibt. Die Form der H

ohenlinien der G

utefunktion und das zul

assige Gebiet

angen vom Zeitschritt k ab, d. h., sie ver

andern sich w

ahrend eines Ausre-

gelvorganges.

5.1.5 Nichtlineare modellbasierte pr

adiktive Regelung

Bei nichtlinearen Regelstrecken

5.1. Modellbasierte pr

adiktive Regelung 241

˙x = f (x, u),

y = g(x)

(5.20)

oder

x(k +1)=f (x(k), u(k)),

y(k)=g(x(k))

(5.21)

lassen sich MPR

ahnlich anwenden wie bei linearen Regelstrecken. Allerdings

sind Implementierung und Ablauf meistens deutlich komplizierter und auf-

wendiger als im linearen Fall. Dies ist darauf zur

uckzuf

uhren, dass das Op-

timierungsproblem aufgrund der nichtlinearen Systemdynamik (5.21) keine

einfache Form mehr aufweist. Insbesondere ist es im Allgemeinen nicht mehr

konvex. Die Nichtlinearit

at der Systeml

osung von Gl. (5.21) verursacht eine

komplexe Abh

angigkeit des G

utefunktionswertes J von den zu optimierenden

Stellgr

oßenwerten u(k + i). Ein solches nicht konvexes Optimierungsproblem

besitzt oft mehrere lokale Minima und es existieren keine sicher konvergenten

osungsverfahren. Das prinzipielle Vorgehen entspricht trotz der komplexeren

Numerik dem Ablauf der LMPR.

Zur L

osung des beschr

ankten Optimierungsproblems verwendet man nu-

merische Optimierungsverfahren [5, 36, 100], wobei eines der Hauptprobleme

oft darin besteht, das Optimierungsproblem in Echtzeit zu l

osen. Als beson-

ders zeitaufwendig stellt sich dabei heraus, dass f

ur jeden Stellgr

oßenverlauf

und jede G

utewertberechnung die L

osung des Systems (5.20) bestimmt wer-

den muss. In der Regel geschieht das im zeitkontinuierlichen Fall (5.20) mittels

eines Integrationsverfahrens, z. B. des Runge-Kutta-Verfahrens. Im Fall dis-

kreter Systeme erfolgt die Berechnung der Systeml

osung unmittelbar

uber die

Rekursionsgleichung (5.21).

Die Echtzeitproblematik hat zur Folge, dass MPR nur bei relativ langsa-

men Regelstrecken, z. B. in der Prozessindustrie, zum Einsatz kommen. Ein

weiteres Problem nichtlinearer MPR, abgek

urzt NMPR, ist die Sicherstellung

der Stabilit

at des Regelkreises. Aufgrund der Nichtlinearit

at der Regelstrecke

und des nicht explizit angebbaren Regelgesetzes kann diese im Allgemeinen

nicht garantiert werden.

Wir betrachten die Stabilit

atsproblematik im Folgenden genauer. Aus-

gangspunkt unserer Betrachtungen ist das System (5.21), wobei der Eingangs-

oßenvektor u gem

aß

u ∈ W ⊂ IR

und der Zustandsvektor x gem

aß

x ∈ X ⊂ IR

beschr

ankt sind. F

ur die NMPR gelte im Weiteren n

= n

. Als zu minimie-

rende G

utefunktion setzen wir die Funktion

J(k)=

k+n

−1



i=k

Q(x(i), u(i))

242 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

an. Dabei kann die Funktion Q z. B. quadratische Bewertungsterme,

ahnlich

denen in Gl. (5.1), besitzen. In jedem Fall muss Q(x, u) > 0f

ur alle x = 0

und u = 0 gelten. Des Weiteren soll das geregelte System in

x(k)=0

ur u(k)=0 eine Ruhelage besitzen und es soll

Q(0, 0)=0

gelten. Aufgrund dieser Forderung gilt insbesondere auch J(k)=0f

ur x(k)=

0 und f

ur u(i)=0,i= k, k +1,...

Wir beachten, dass das G

utemaß J mittelbar nur vom Zustandsvektor x

abh

angt, da der Stellgr

oßenvektor u

uber die NMPR von x abh

angt. Somit

scheint uns die G

utefunktion J eine Kandidatin f

ur eine Ljapunov-Funktion

des pr

adiktiv geregelten Systems zu sein. Denn sie ist im Ursprung x =

identisch null und sonst

uberall positiv. Als dritte Bedingung einer Ljapunov-

Funktion (siehe Abschnitt 2.4.4) muss J noch die Forderung

J(k) − J(k − 1) < 0 (5.22)

erf

ullen, d. h., J(k) muss im Verlauf jedes Ausregelvorganges abnehmen.

Die Bedingung (5.22) ist auch erf

ullt, wenn J(k) nur wenig kleiner ist als

J(k − 1). Dann erfolgt die Ausregelung aber sehr langsam. Scokaert, Mayne

und Rawlings [165] versch

arfen die Bedingung (5.22) daher zu

J(k) − J(k − 1) < − μQ(x(k − 1), u(k − 1)), (5.23)

wobei μ ∈ (0, 1) gilt.

ur Werte μ nahe null wird die Optimierungsprozedur leichter eine L

osung

u(k),...,u(k + n

− 1) ﬁnden als f

ur große Werte μ,weilesindiesemFall

mehr L

osungen gibt. Der Preis, der hierf

ur zu zahlen ist, besteht in einer oft

nur geringen Abnahme des G

utewertes J. Folglich ist die Ausregelung dann

wieder langsam.

ahlt man μ nahe bei eins, so ist die Abnahme von J von einem Schritt

k −1zumn

achsten gr

oßer. Allerdings ist nun der L

osungsraum st

arker einge-

schr

ankt, so dass die Berechnung einer L

osung komplizierter wird und l

anger

dauern kann.

ahrend der Ausf

uhrung der MPR muss st

andig

uberpr

uft werden, ob

die Ungleichung (5.23) eingehalten wird. Sobald die Optimierungsprozedur

eine entsprechende Stellgr

oßenfolge u(k),...,u(k + n

−1) gefunden hat, sind

zwei F

alle denkbar. Im ersten steht noch Optimierungszeit zur Verf

ugung.

Sie kann benutzt werden, um das Ergebnis zu verbessern. Im zweiten ist die

zur Verf

ugung stehende Optimierungszeit verbraucht und die Stellgr

oße u(k)

wird auf die Regelstrecke geschaltet. Die Optimierung startet dann erneut

mit

k = k + 1 und sucht eine neue Kombination von Werten u(

k),...,u(

k +

5.1. Modellbasierte pr

adiktive Regelung 243

− 1). G

unstigerweise benutzt man dabei den alten Satz von Stellgr

oßen

u(k),...,u(k + n

− 1) als Startpunkt der Optimierung.

Die G

utefunktion J ist zwar als Ljapunov-Funktion geeignet, jedoch

onnen wir ihre Abnahme entlang einer Trajektorie, d. h. die Erf

ullung der

Ungleichung (5.22), nur numerisch w

ahrend eines Ausregelvorganges feststel-

len. Der Stabilit

atssatz von Ljapunov fordert aber f

ur den Nachweis der Sta-

bilit

at die

Uberpr

ufung der Bedingung (5.22) in einer Umgebung U (0)der

Ruhelage x

= 0,d.h.f

ur alle x ∈ U(0) \{0} und nicht nur f

ur einzelne

Trajektorien. Da wir die Abnahme von J jedoch nur f

ur einzelne Trajektorien

und nicht in der gesamten Umgebung von x = 0 pr

ufen k

onnen, ist die obige

Vorgehensweise nicht hinreichend f

ur den Stabilit

atsnachweis.

Obige Problematik l

asst sich an einem Gedankenbeispiel veranschaulichen.

Wir betrachten einen nichtlinearen modellpr

adiktiven Regelkreis zweiter Ord-

nung. Er besitzt eine Ruhelage bei x = 0 und einen kreisf

ormigen stabilen

Grenzzyklus mit einem Mittelpunkt bei x = 0. Wir starten den Ausregelvor-

gang mittels des pr

adiktiven Reglers, wie wir ihn oben beschrieben haben, in

einem Punkt x

außerhalb des Grenzzyklus. Die Trajektorie x(k)desRegel-

kreises l

auft nun vom Punkt x(0) asymptotisch in den Grenzzyklus hinein.

Dabei nimmt das G

utemaß J best

andig ab, so dass die Ungleichung (5.22)

oder (5.23) erf

ullt ist. Die Trajektorie x(k)l

auft also trotz der Abnahme von

J nicht in die Ruhelage x

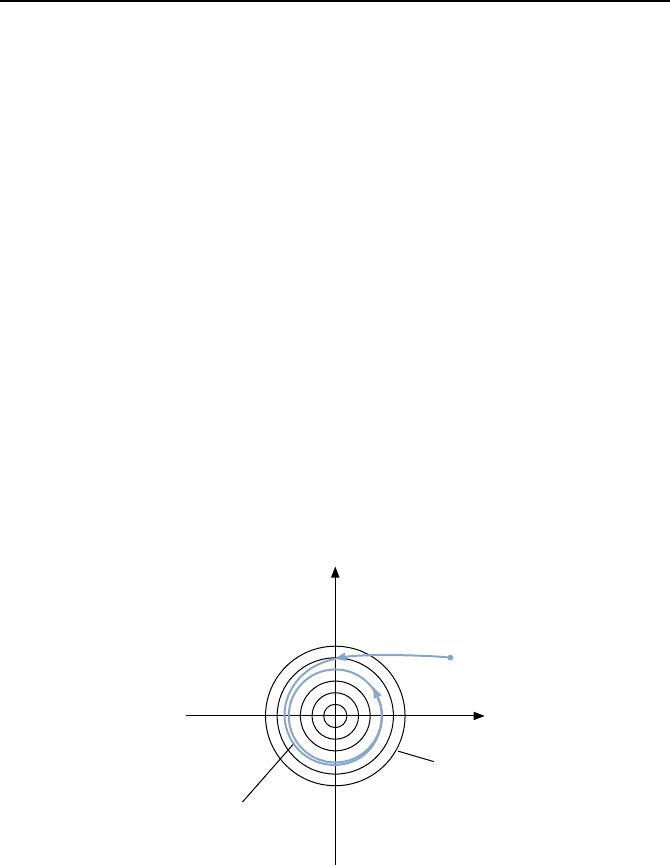
= 0. Bild 5.8 illustriert diesen Sachverhalt.

x(0)

x(k)

Grenzzyklus

Niveaulinie von J

Bild 5.8: Beispiel f

ur die kontinuierliche Abnahme des G

uteintegrals J entlang einer

Trajektorie, ohne dass die Trajektorie x(k) gegen null strebt.

Halten wir als Res

umee fest, dass wir nicht feststellen k

onnen, ob das

utemaß J eine Ljapunov-Funktion ist. Die Abnahme von J w

ahrend einer

Ausregelung bildet lediglich eine praxisorientierte Bedingung f

ur die Stabilit

des pr

adiktiven Regelungssystems. Um nun sicherstellen zu k

onnen, dass die

Ruhelage x

= 0 auch wirklich erreicht wird, d. h. Stabilit

at vorliegt, fordern

244 Kapitel 5. Regelungen f

ur lineare und nichtlineare Regelstrecken

wir zus

atzlich zur Abnahme von J noch

x(k + n

)=0 (5.24)

in jedem Zeitschritt k.

Gleichung (5.24) ist eine weitere Nebenbedingung in der Optimierungsauf-

gabe. Um sie zu erf

ullen, muss der Stellhorizont n

ausreichend groß sein. Dies

kann sehr große Werte n

erfordern, wodurch die Anzahl der zu optimierenden

Stellgr

oßenwerte u(k),...,u(k + n

− 1) ebenfalls sehr groß wird.

Die letztere Problematik wird abgeschw

acht, wenn man anstelle der Re-

striktion (5.24) fordert, dass

x(k + n

) ∈ U (0)

gilt, wobei U(0) eine Umgebung der Ruhelage x

= 0 ist. U(0) kann dabei

ein Toleranzgebiet sein, dessen Zustandswerte x ∈ U(0) man als Zielwerte

der Regelung akzeptiert, weil ihre Abweichung von x = 0 hinreichend klein

ist. Die Umgebung U(0) kann aber auch ein Gebiet sein, in dem man anstelle

der pr

adiktiven Regelung u

(x) einen anderen Regler u

(x) verwendet. In

diesem Fall legt man den Regler u

(x)soaus,dasserf

ur alle x ∈ U (0)zueiner

stabilen Ausregelung in die Ruhelage x

= 0 f

uhrt. Die Umgebung U (0)wird

dabei als Ljapunov-Gebiet ausgelegt. Keine Trajektorie x(k)verl

asst U(0)

dann wieder. Eine Ausregelung f

ur ein x

∈ U (0)beginntmitderpr

adiktiven

Regelung u

(x) und schaltet auf den zweiten Regler u

(x)um,sobaldx(k) ∈

U(0) gilt. Bild 5.9 illustriert dieses Regelgesetz.

Das Regelgesetz u

(x) kann man z. B. linear auslegen, wobei man eine um

x = 0 linearisierte Streckenbeschreibung zugrunde legt. Regelungen dieser Art

mit zwei Regelgesetzen u

und u

bezeichnet man als Dual-mode-Regler .Obi-

Uberlegungen k

onnen wir in dem von Scokaert, Mayne und Rawlings [165]

Umschaltung

auf u

adiktive

Regelung u

Bild 5.9: Pr

adiktive Dual-mode-Regelung.

5.1. Modellbasierte pr

adiktive Regelung 245

vorgeschlagenen nachfolgenden Dual-mode-MPR-Algorithmus zusammenfas-

sen:

Schritt 1: W

ahle ein μ ∈ (0, 1).

Schritt 2: Sei k =0.Wennx(0) ∈ U (0), dann setze u(0) = u

(x(0)).

Andernfalls ﬁnde durch Optimierung von J eine Stellgr

oßenfolge

u(0), u(1),...,u(n

− 1)

mit einer zugeh

origen Zustandsgr

oßenfolge

x(0), x(1),...,x(n

so dass

u(i) ∈ W f

ur alle i =0,...,n

− 1,

x(i) ∈ X f

ur alle i =0,...,n

x(n

) ∈ U(0)

gilt. Verwende als aktiven Stellgr

oßenwert u(0).

Schritt 3: Sei k =0.Wennx(k) ∈ U(0), dann setze u(k)=u

(x(k)).

Andernfalls ﬁnde durch Optimierung von J eine Stellgr

oßenfolge

u(k),...,u(k + n

− 1)

mit einer zugeh

origen Zustandsgr

oßenfolge

x(k),...,x(k + n

so dass

u(i) ∈ W f

ur alle i = k,...,k+ n

− 1,

x(i) ∈ X f

ur alle i = k,...,k+ n

x(k + n

) ∈ U(0)

und

J(k) − J(k − 1) < −μQ(x(k − 1), u(k − 1))

gilt. Bei der Optimierung von J w

ahlt man die Stellgr

oßenfolge

des vorherigen Schrittes als Startpunkt. Verwende als aktiven Stell-

oßenwert u(k). Wiederhole Schritt 3.

Es soll an dieser Stelle nicht verschwiegen werden, dass Stabilit

atsuntersuch-

ungen bei nichtlinearen MPR in der industriellen Praxis oft vernachl

assigt