J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.


6.3. Beobachterentwurf mittels Linearisierung 307
Zellkultur
Pumpe
Glucose
Bild 6.7: Bioreaktor.
mit der Wachstumsrate μ
0
=1h
−1
und den beiden Affinit
¨
atskonstanten k
1
=
0.03 g l
−1
, k
2
=0.5lg
−1
ab. Die Konzentration x
2
wird in g l
−1
gemessen.
Der auf das Gesamtvolumen bezogene Substratzufluss u,gemesseninh
−1
,
verd
¨
unnt die Biomasse um den Wert
−x
1
· u.
Damit ergibt sich f
¨
ur die zeitliche
¨
Anderung der Biomassekonzentration
˙x
1
= μ(x
2
) · x
1
− x
1
· u.
Die Substratmasse wird im Reaktor von der Biomasse verbraucht und nimmt
daher proportional zur Zellkulturmenge x
1
ab. Der Substratzufluss erh
¨
oht die
Substratkonzentration x
2
im Reaktor proportional zum Zufluss u und der
Differenz der Konzentration K der Glucose im Zulauf und der Konzentration
x
2
im Reaktor. Also gilt
˙x
2
= −
1
α
μ(x
2
) · x
1
+(K − x
2
) · u
mit dem Ausbeutekoeffizient α =0.5 und der Zulaufkonzentration der Glucose
K =10gl
−1
.
Zusammengefasst ergibt sich als Zustandsraummodell
˙x = a(x)+b(x) · u =
+
μ(x
2
) · x
1
−
1
α
μ(x
2
) · x
1
,
+
−x
1
K − x
2
u,
y = g(x)=
10
x .
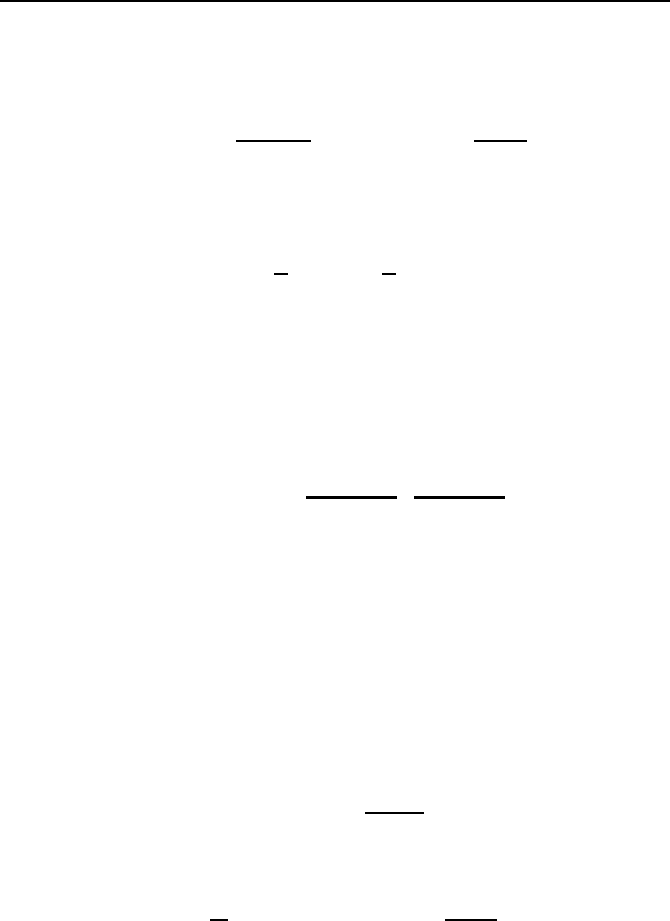
308 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
Im Folgenden soll nun ein Beobachter mittels Linearisierung und zustands-
abh
¨
angiger Beobachtermatrix L(˜x,u) entworfen werden. F
¨
ur den Beobach-
terentwurf sind zuerst einmal f
¨
ur die Linearisierung des Systems die Jacobi-
Matrizen
A(˜x,u)=
∂f(˜x,u)
∂ ˜x
und C(˜x)=
∂g(˜x)
∂ ˜x
zu bilden. Man erh
¨
alt
A(˜x,u)=
⎡
⎢
⎣
μ(˜x
2
) − uμ
(˜x
2
)˜x
1
−
1
α
μ(˜x
2
) −
1
α
μ
(˜x
2
)˜x
1
− u
⎤
⎥
⎦
und
C(˜x)=
10
.
Im n
¨
achsten Entwurfsschritt berechnet man das charakteristische Polynom
der Beobachtermatrix
P (s)=det(sI − (A(˜x,u) − L(˜x,u)C(˜x))
Beobachtermatrix F (˜x,u)
).
Hierbei ist
L(˜x,u)=
l
1
(˜x,u)
l
2
(˜x,u)
.
Wir verwenden der
¨
Ubersichtlichkeit halber im Weiteren die folgenden
Abk
¨
urzungen:
l
1
= l
1
(˜x,u),
l
2
= l
2
(˜x,u),
μ = μ(˜x
2
),
μ
= μ
(˜x
2
)=
dμ(˜x
2
)
d˜x
2
.
Man erh
¨
alt so f
¨
ur das charakteristische Polynom von F
P (s)=s
2
+
l
1
− μ +
μ
α
˜x
1
+2u
s + μ
˜x
1
l
2
+
l
1
+ u
α
+ l
1
u − μu + u
2
.
Der Koeffizientenvergleich mit dem Wunschpolynom
ˆ
P (s)=s
2
+ˆa
1
s +ˆa
0
liefert das Gleichungssystem
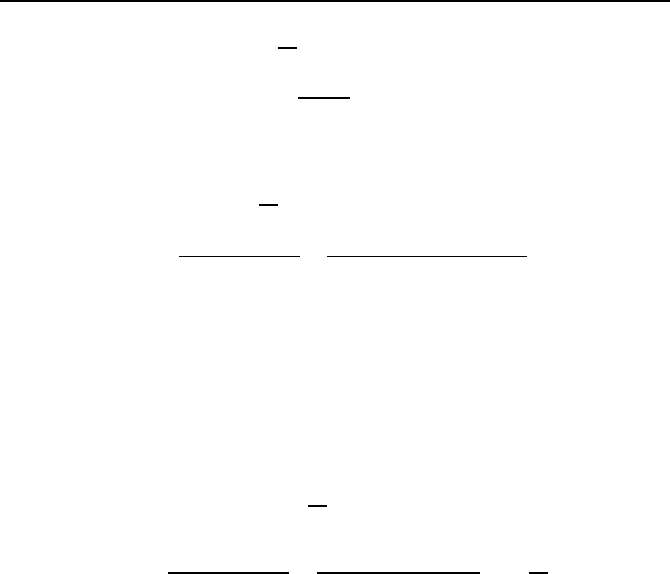
6.3. Beobachterentwurf mittels Linearisierung 309
ˆa
1
= l
1
− μ +
μ
α
˜x
1
+2u,
ˆa
0
= μ
˜x
1
l
2
+
l
1
+ u
α
+ l
1
u − μu + u
2
.
Hieraus folgt
l
1
=ˆa
1
+ μ −
μ
α
˜x
1
− 2u,
l
2
=
ˆa
0
− ˆa
1
u + u
2
μ
˜x
1
−
ˆa
1
+ μ − α
−1
μ
˜x
1
− 2u
α
.
In der Tat ergibt sich nach Einsetzen von L(˜x,u) in die Gl. (6.11) f
¨
ur die
Matrix F der Sch
¨
atzfehlergleichung
˙e = F (˜x,u)e
die von ˜x und u abh
¨
angige Matrix
F (˜x,u)=A(˜x,u) − L(˜x,u) C(˜x)
=
⎡
⎢
⎢
⎢
⎣
−ˆa
1
+
μ
α
˜x
1
+ uμ
˜x
1
−
ˆa
0
− ˆa
1
u + u
2
μ
˜x
1
+
ˆa
1
− α
−1
μ
˜x
1
− 2u
α
−
μ
α
˜x
1
− u
⎤
⎥
⎥
⎥
⎦
.
Man beachte, dass zwar F von ˜x und u abh
¨
angt, aber das charakteristische
Polynom
P (s)=
ˆ
P (s)=s
2
+ˆa
1
s +ˆa
0
der Matrix F nicht abh
¨
angig von ˜x und u ist.
Wir legen den Beobachter mittels ˆa
0
= 100 und ˆa
1
=20soaus,dassdie
Eigenwerte von F (˜x,u) bzw. die Nullstellen des charakteristischen Polynoms
P bei s
1/2
= −10 liegen.
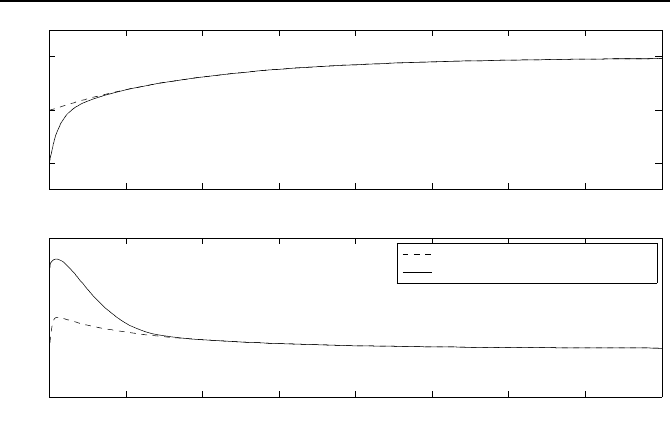
Die Diagramme in Bild 6.8 zeigen den Verlauf der Biomasse- und Sub-
stratkonzentration im Bioreaktor f
¨
ur den Anfangszustand
x(0) = [4.00.02]
T
gl
−1
.
Zum Vergleich sind die Systemzust
¨
ande des Beobachters angegeben, ausge-
hend von
˜x(0) = [3.00.05]
T
gl
−1
.
Die Systemzust
¨
ande n
¨
ahern sich bei einer Eingangsgr
¨
oße u =0.5 den End-
werten x
1
=4.94 g l
−1
und x
2
=0.03 g l
−1
an. Die Fehler zwischen den rea-
len Systemzust
¨
anden des Reaktors und den beobachteten werden schnell und
recht unspektakul
¨
ar eliminiert.
310 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
Zeit t in Stunden
5
4
3
0.1
0
0
0
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
Zustandsgr
¨
oße
gesch
¨
atzte Zustandsgr
¨
oße
x
1
in gl
−1
x
2
in gl
−1
Bild 6.8: Verlauf der tats
¨
achlichen und der gesch
¨
atzten Biomassekonzentrationen x
1
und Substratkonzentrationen x
2
.
6.4 Das erweiterte Kalman-Filter
6.4.1 Kalman-Filter f
¨
ur lineare Systeme
Das erweiterte Kalman-Filter, abgek
¨
urzt EKF, ist der in der Praxis am h
¨
au-
figsten verwendete Beobachtertyp f
¨
ur nichtlineare Systeme. Es basiert auf
einer linearisierten Darstellung der nichtlinearen Systemdynamik. Um seine
Funktionsweise zu verstehen, wird zuerst kurz die Funktionsweise des Kalman-
Filters f
¨
ur lineare Systeme wiederholt [53].
Das zu beobachtende System
˙x = Ax + Bu + μ,
y = Cx + ρ
wird durch zwei mittelwertfreie, normalverteilte, weiße Rauschprozesse μ und
ρ, die unkorreliert sind, gest
¨
ort. F
¨
ur ihre beiden Kovarianzmatrizen Q und S
gilt
cov{μ(t
1
), μ(t
2
)} = Q · δ(t
1
− t
2
),
cov{ρ(t
1
), ρ(t
2
)} = S · δ(t
1
− t
2
).
Das Kalman-Filter
˙
˜x =(A − LC) ˜x + Bu + Ly
6.4. Das erweiterte Kalman-Filter 311
u
y
˜y
v
˜x
y − ˜y
L
˙x = Ax + Bu + μ
y = Cx + ρ
˙
˜x = A ˜x + Bu + v
˜y = C ˜x
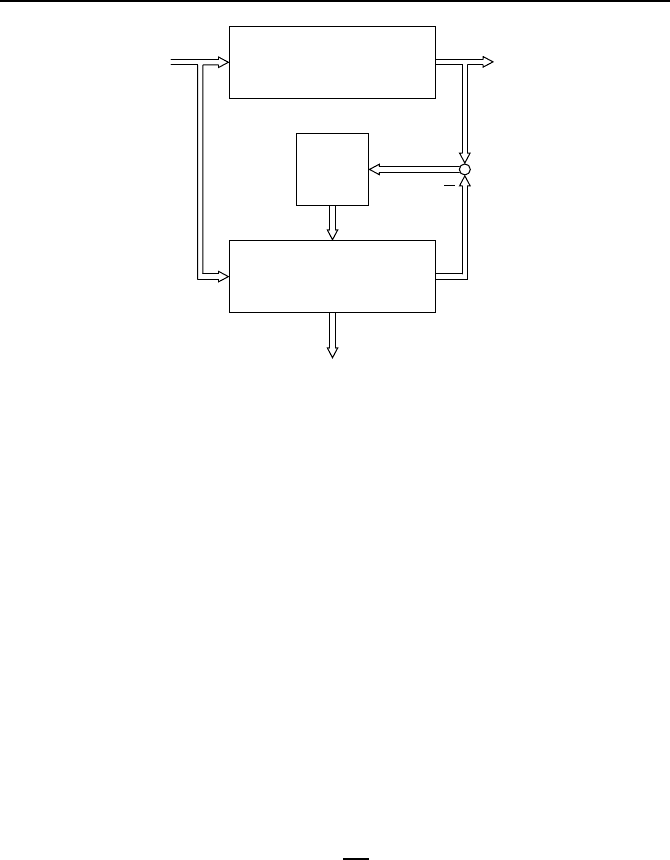
Bild 6.9: Struktur eines Kalman-Filters.
mit der Filtermatrix L bestimmt mit ˜x eine Sch
¨
atzung des Zustandsgr
¨
oßenvek-
tors x. Bild 6.9 zeigt das zu beobachtende System und die Struktur des
Kalman-Filters, die vollst
¨
andig der Struktur des Luenberger-Beobachters aus
Bild 6.1 entspricht.
In der Tat sind, wie wir aus der linearen Systemtheorie wissen [53, 182],
Kalman-Filter und Luenberger-Beobachter identisch in ihren Gleichungen. Sie
unterscheiden sich lediglich in der Bestimmung der Matrix L.Undzwarw
¨
ahlt
man beim Luenberger-Beobachter die Eigenwerte geeignet und legt dadurch
die Matrix L fest. Die Kalman-Matrix L ist dagegen so ausgelegt, dass der
Einfluss der Rauschgr
¨
oßen μ und ρ auf den Sch
¨
atzfehler e minimal ist. Dies
geschieht, indem man aus dem Sch
¨
atzfehler
e = x − ˜x
und den Erwartungswerten
E
&
e
2
i
'
= lim
T →∞
1
2T
T
−T
e
2
i
(t)dt
das G
¨
utemaß
J =
n
i=1
E
&
e
2
i
'
bildet und dieses in Abh
¨
angigkeit von L minimiert.
Die L
¨
osung hat die Form
L = PC
T
S
−1
, (6.12)

312 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
wobei sich P aus der Riccati-Gleichung
AP + PA
T
− PC
T
S
−1
CP = −Q (6.13)
ergibt. Die Matrizen S und Q sind im Allgemeinen unbekannt und werden
oft als Einheitsmatrizen angenommen. Erst nachtr
¨
agliches, iteratives Auspro-
bieren bzw. Optimieren mit anderen Matrizen S und Q f
¨
uhrtdannzueinem
befriedigenden Entwurfsergebnis.
6.4.2 Das EKF f
¨
ur nichtlineare Systeme
Im Fall eines nichtlinearen Systems
˙x = f (x, u)+μ,
y = g(x, u)+ρ
kann formal die Sch
¨
atzgleichung des Kalman-Filters auf die nichtlineare Si-
tuation
¨
ubertragen werden und man erh
¨
alt die Beobachtergleichung
˙
˜x = f (˜x, u)+L(y − g(˜x)).
Dieser Analogieschritt wurde bereits im vorherigen Kapitel im Fall des Be-
obachterentwurfes mittels Linearisierung durchgef
¨
uhrt. Nachteilig ist dabei
die Wahl einer konstanten Matrix L, da der Beobachter dann nur um einen
Arbeitspunkt herum gut funktionieren wird. Diese Situation liegt auch hier
vor. Man w
¨
ahlt die Beobachtermatrix L daher zeitabh
¨
angig, um sie je nach
Verlauf der Trajektorien x(t)bzw.˜x(t) an die Nichtlinearit
¨
at des Systems
anzupassen. So nimmt die Beobachtergleichung die Form
˙
˜x = f(˜x, u)+L(t)(y − g(˜x)) (6.14)
an. Diesen Beobachter bezeichnet man als erweitertes Kalman-Filter.
Der Entwurf von L(t) erfolgt mittels der bekannten Entwurfsgleichung
(6.12) des klassischen Kalman-Filters
L(t)=P (t)C
T
(t)S
−1
,
wobei sich die Matrix P (t) aus der nun zeitabh
¨
angigen Riccati-Gleichung
(6.13)
A(t)P (t)+P (t)A
T
(t) − P (t)C
T
(t)S
−1
C(t)P (t)=−Q
errechnet. Dabei ergeben sich die Matrizen A(t) und C(t) als Linearisierun-
gen, d. h. Taylor-Entwicklungen, die nach dem ersten Glied abgebrochen wer-
den, aus
A(t)=
∂f
∂x
˜x(t)
und C(t)=
∂g
∂x
˜x(t)

6.4. Das erweiterte Kalman-Filter 313
an der jeweils aktuellen und bekannten St
¨
utzstelle ˜x(t).
Praktisch l
¨
ost man die obige algebraische Riccati-Gleichung wie im linea-
ren Fall
¨
uber die Riccati-Differenzialgleichung
˙
P (t)=A(t)P (t)+P (t)A
T
(t)+Q − P (t)C
T
(t)S
−1
C(t)P (t). (6.15)
Als Anfangswert f
¨
ur die gesuchte Matrix P (t) wird dabei die Kovarianzmatrix
P (0) = cov{x
0
− ˜x
0
, x
0
− ˜x
0
} =E{(x
0
− ˜x
0
)(x
0
− ˜x
0
)
T
}
des anf
¨
anglichen Sch
¨
atzfehlers
e
0
= x
0
− ˜x
0
, x
0
= x(0) und ˜x
0
= ˜x(0)
verwendet.
Zu beachten ist, dass die Riccati-Differenzialgleichung (6.15) nicht offline
gel
¨
ost wird, um den station
¨
aren Wert von P zu bestimmen. Dies ist off-
line deshalb nicht m
¨
oglich, weil sich A(t) fortlaufend
¨
andert. Man l
¨
ost die
Sch
¨
atzgleichung (6.14) und die Riccati-Differenzialgleichung (6.15) also si-
multan, wobei man fortw
¨
ahrend die Jacobi-Matrizen A(t) und C(t)zube-
stimmen hat. Stabilit
¨
at und Qualit
¨
at der Sch
¨
atzung sind beim erweiterten
Kalman-Filter nicht gesichert, sondern m
¨
ussen simulatorisch
¨
uberpr
¨
uft wer-
den. Letzteres hat den Nachteil, dass man keine allgemeing
¨
ultige Aussage
erh
¨
alt, sondern Stabilit
¨
at und Sch
¨
atzg
¨
ute nur f
¨
ur die jeweils durchgef
¨
uhrten
speziellen Simulationen gelten.
Beim Entwurf des Kalman-Filters, d. h. der Wahl von S und Q,istAus-
probieren n
¨
otig und Erfahrung erforderlich. Zusammengefasst erh
¨
alt man f
¨
ur
das System
˙x = f (x, u)+μ,
y = g(x, u
)+ρ
die Gleichungen des erweiterten Kalman-Filters bzw. des Beobachters
˙
˜x = f (˜x, u)+L(y − g(˜x)),
A =
∂f
∂x
˜x(t)
,
C =
∂g
∂x
˜x(t)
,
˙
P = AP + PA
T
+ Q − PC
T
S
−1
CP,
L = PC
T
S
−1
.
(6.16)
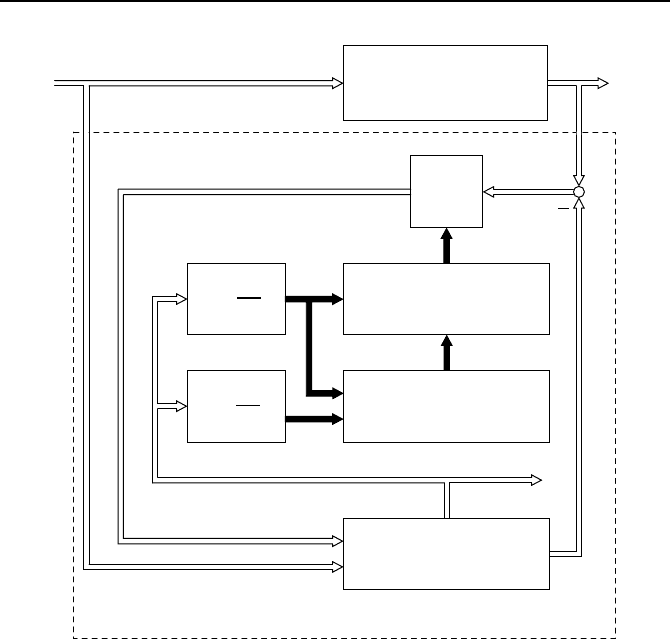
Die Struktur des erweiterten Kalman-Filters und die gegenseitigen Abh
¨
angig-
keiten der einzelnen Gleichungen zeigt Bild 6.10.
314 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
y
˜y
y − ˜y
˜x
˜x
L
L
P
v
C
A
˙x = f (x, u)+μ
y = g(x)+ρ
˙
P =AP + PA
T
+ Q
−PC
T
S
−1
CP
A =
∂f
∂x
˛
˛
˛
˛
˜x
C =
∂g
∂x
˛
˛
˛
˛
˜x
L = PC
T
S
−1
˙
˜x = f (˜x, u)+v
˜y = g(˜x)
u
u
System
Modell
Erweitertes Kalman-Filter
Bild 6.10: Erweitertes Kalman-Filter.
Die praktische Umsetzung des erweiterten Kalman-Filters erfordert, wenn
man von sehr einfachen F
¨
allen absieht, eine numerische L
¨
osung der Riccati-
Differenzialgleichung mittels eines Integrationsverfahrens – z. B. mittels des
Runge-Kutta-Verfahrens. Im Prinzip gilt dies auch f
¨
ur die Sch
¨
atzgleichung.
Die numerische L
¨
osung der Riccati-Differenzialgleichung kann dabei Probleme
bereiten.
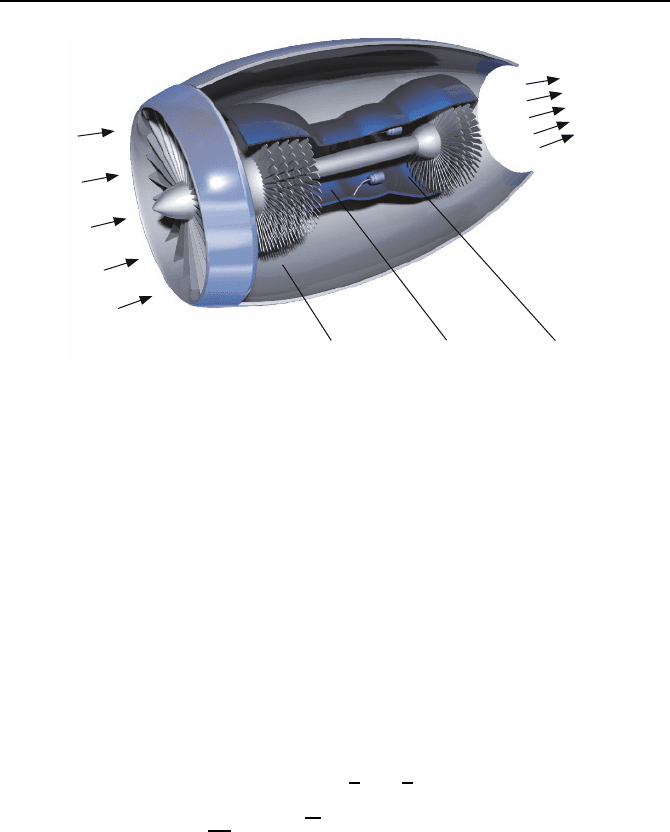
6.4.3 Beispiel Flugzeugtriebwerk
Wir betrachten ein Strahltriebwerk, wie es z. B. in Verkehrsflugzeugen einge-
setzt wird. Bei dem in Bild 6.11 gezeigten Mantelstromtriebwerk, auch Tur-
bofan genannt, existieren ein innerer und ein
¨
außerer Luftstrom. Der innere
Luftstrom, auch Kernstrom genannt, wird durch einen Kompressor verdich-
tet, dann mit Kerosin vermischt und dieses Gemisch hinter dem Kompressor
gez
¨
undet. Die so entstandenen Verbrennungsgase treiben eine Gasturbine an.
6.4. Das erweiterte Kalman-Filter 315
Schub
Mantelstrom
Kernstrom
Verbrennungsraum
Bild 6.11: Flugzeugtriebwerk.
Diese wiederum dreht den Kompressor und den vor ihm liegenden Fan. Der
Fan saugt neben der Luft des inneren Stroms auch die des
¨
außeren an, der
mantelf
¨
ormig um den Kompressor und die Turbine herumgeleitet wird. Die-
ser
¨
außere Luftstrom, der Mantelstrom, verst
¨
arkt den Schub, der durch den
Kernstrom erzeugt wird.
Im Kompressor kann es aufgrund eines Str
¨
omungsabrisses oder durch
Schubschwankungen zu instabilen Str
¨
omungsverh
¨
altnissen kommen. Dann
sind im schlimmsten Fall Besch
¨
adigungen des Triebwerks, z. B. aufgrund eines
Flammenaustrittes oder aufgrund einer Richtungsumkehr des Massenstroms,
m
¨
oglich. Dies sucht man z. B. durch eine Regelung zu vermeiden.
Beschrieben werden die Verh
¨
altnisse im Kompressor durch die Moore-
Greitzer-Gleichungen [105, 126]
˙
Φ = − Ψ + Ψ
co
+1+
3
2
Φ −
1
2
Φ
3
− 3ΦR,
˙
Ψ =
1
β
2
(Φ − γ
√
Ψ +1),
˙
R = σR(1 − Φ
2
− R).
(6.17)
Hierbei ist Φ der Massenfluss durch den Kompressor, Ψ der Druckanstieg,
R ≥ 0isteinMaßf
¨
ur den Str
¨
omungsabriss und β, σ sowie Ψ
co
sind Kon-
stanten. Als Stellgr
¨
oße u wirkt die Variable γ.Sierepr
¨
asentiert z. B. Zapfluft,
die dem Kernstrom oder dem Mantelstrom entnommen und dem Verdichter
so zugef
¨
uhrt wird, dass kein Str
¨
omungsabriss oder eine Richtungsumkehr des
Massenstroms entsteht.
Ziel ist es, mittels einer Regelung das Triebwerk, d. h. seinen Kompressor,
in der Ruhelage
316 Kapitel 6. Beobachter f
¨
ur nichtlineare Systeme
R
R
=0,Φ
R
= 1 und Ψ
R
= Ψ
co
+ 2 (6.18)
bei γ =2/
√
Ψ
co
+ 2 zu stabilisieren. Dies geschieht z. B. mit einem nichtlinea-
ren Zustandsregler. Allerdings ben
¨
otigt man f
¨
ur einen solchen Regler alle drei
Zustandsgr
¨
oßen Φ, Ψ und R. Der Druckanstieg Ψ ist messbar. Die Gr
¨
oßen Φ
und R hingegen sind es nicht. Sie m
¨
ussen mittels eines Beobachters gesch
¨
atzt
werden.
Bevor wir ein erweitertes Kalman-Filter als Beobachter entwerfen, trans-
formieren wir das System (6.17) noch so, dass die Ruhelage (6.18) im Ursprung
liegt. Zu diesem Zweck f
¨
uhren wir die neuen Zustandsvariablen
x
1
= Φ − 1,
x
2
= Ψ − Ψ
co
− 2,
x
3
= R
ein und erhalten mit u = γ die transformierten Systemgleichungen
⎡
⎣
˙x
1
˙x
2
˙x
3
⎤
⎦
= f(x,u)=
⎡
⎢
⎢
⎢
⎣
−x
2
−
3
2
x
2
1
−
1
2
x
3
1
− 3x
1
x
3
− 3x
3
1
β
2
x
1
− u
x
2
+ Ψ
co
+2+2
!
−σx
2
3
− σx
3
(2x
1
+ x
2
1
)
⎤
⎥
⎥
⎥
⎦
. (6.19)
Die Messgr
¨
oße ist, wie erw
¨
ahnt, y = x
2
. In der Ruhelage x
R
= 0 betr
¨
agt
u
R
=2/
√
Ψ
co
+2.
Wir linearisieren das System (6.19) um den gesch
¨
atzten Zustand
˜
x herum
und erhalten
A(t)=
∂f
∂x
˜
x
=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
−3˜x
1
−
3
2
˜x
2
1
− 3˜x
3
−1 −3˜x
1
− 3
β
−2
− β
−2
u
2
(˜x
2
+ Ψ
co
+2)
0
−2σ˜x
3
(1 + ˜x
1
)0−2σ˜x
3
− σ(2˜x
1
+˜x
2
1
)
⎤
⎥
⎥
⎥
⎥
⎥
⎦
und mit
y = g(x)=x
2
ergibt sich
C(t)=
∂g
∂x
˜x
=[010].
Die linearisierte Systemmatrix A(t), der linearisierte Ausgangsvektor C(t)
und die nichtlineare Systemdynamik f (x,u) sind nun einzusetzen in die Glei-
chungen (6.16) des erweiterten Kalman-Filters. Man erh
¨
alt
˙
˜x = f(
˜
x,u)+L(y − ˜x
2
),
˙
P = AP + PA
T
+ Q − PC
T
S
−1
CP,
L = PC
T
S
−1
.
