J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.


186 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
und schaltet die Spannungen der beiden Elektromagneten gem
¨
aß
u
1
=
v f
¨
ur φ<0,
0f
¨
ur φ ≥ 0
(4.25)
und
u
2
=
0f
¨
ur φ<0,
−v f
¨
ur φ ≥ 0
(4.26)
ein und aus. Die Spannung v ist variabel und bildet die Stellgr
¨
oße u =
˙
φ = v/N
des noch zu entwerfenden Reglers.
Die auf die Welle wirkende Gesamtkraft ist mit Verwendung von Gl. (4.21)
durch
F
g
= F
1
− F
2
=
1
μ
0
A
(Φ
2
1
− Φ
2
2
)
gegeben. F
¨
ur die in obiger Gleichung auftretende Differenz Φ
2
1
− Φ
2
2
ergibt
sich aus den Gleichungen (4.22), (4.23) und (4.24) unter Ber
¨
ucksichtigung
der Schaltstrategien (4.25) und (4.26) nach einer Zwischenrechnung [184] die
Beziehung
Φ
2
1
− Φ
2
2
=2
¯
Φ
0
φ + φ|φ|
mit
¯
Φ
0
= Φ
0
+min{φ
1
(0),φ
2
(0)}.
Somit erh
¨
alt man f
¨
ur die Beschleunigung
¨
h der Welle mit der Masse m die
Beziehung
¨
h =
1
μ
0
Am
(2
¯
Φ
0
φ + φ|φ|). (4.27)
Definiert man als Zustandsvariablen des Systems x
1
= h, x
2
=
˙
h und
x
3
= φ sowie als Stellgr
¨
oße, wie erw
¨
ahnt, die Spannung u = v/N,soergibt
sich mit x =[x
1
x
2
x
3
]
T
und Gl. (4.27) sowie
˙
φ = u als eingangslineares
Zustandsraummodell
˙x =
⎡
⎣
x
2
α
1
x
3
+ α
2
x
3
|x
3
|
0
⎤
⎦
a(x)
+
⎡
⎣
0
0
1
⎤
⎦
b(x)
u.
F
¨
ur die Parameter gilt α
1
=2
¯
Φ
0
/(μ
0
Am) und α
2
=1/(μ
0
Am). Als Aus-
gangsgr
¨
oße y des Magnetlagers ist die Auslenkung h,also
y = c(x)=x
1
,
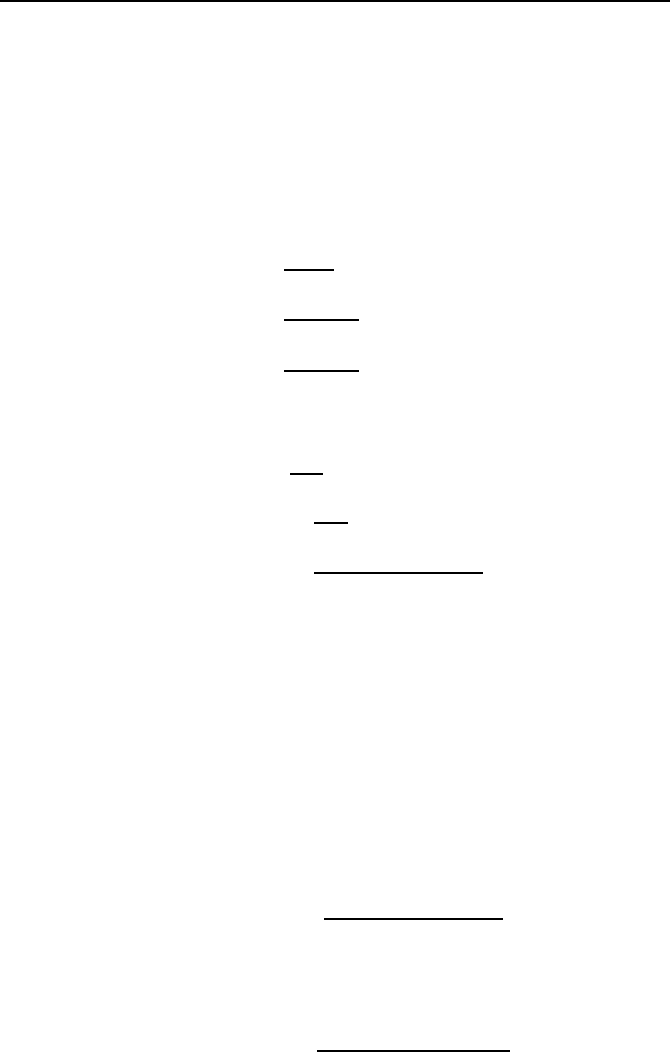
4.2. Reglerentwurf mittels exakter Linearisierung 187
zu betrachten.
Wir entwerfen nun einen Regler mittels exakter Linearisierung gem
¨
aß Satz
18. Dabei ber
¨
ucksichtigen wir, dass die Funktion f(x)=x|x| differenzierbar
ist und die Ableitung f
(x)=2|x| besitzt. Wir gehen in den folgenden Schrit-
ten vor:
Schritt 1: Die Lie-Derivierten L
i
a
c(x)lauten
i =0: L
0
a
c(x)=c(x)=x
1
,
i =1: L
a
c(x)=
∂c(x)
∂x
a(x)=x
2
,
i =2: L
2
a
c(x)=
∂L
a
c(x)
∂x
a(x)=α
1
x
3
+ α
2
x
3
|x
3
|,
i =3: L
3
a
c(x)=
∂L
2
a
c(x)
∂x
a(x)=0.
Schritt 2: Mit den Ergebnissen aus Schritt 1 ermitteln wir die Terme
i =0: L
b
c(x)=
∂x
1
∂x
b(x)=0,
i =1: L
b
L
a
c(x)=
∂x
2
∂x
b(x)=0,
i =2: L
b
L
2
a
c(x)=
∂(α
1
x
3
+ α
2
x
3
|x
3
|)
∂x
b(x)=α
1
+2α
2
|x
3
|.
Also ist f
¨
ur i =2derTermL
b
L
i
a
c(x) ungleich null und δ =3=n.
Schritt 3: Es gilt
L
b
L
2
a
c(x)=α
1
+2α
2
|x
3
| =0
f
¨
ur alle x ∈ IR
3
,daα
1
> 0, α
2
> 0 und |x
3
|≥0ist.
Schritt 4: Da die Differenzordnung hier δ = 3 ist, hat die
¨
Ubertragungsfunk-
tion G(s) des Regelkreises ebenfalls die Ordnung drei, man erh
¨
alt
daher
G(s)=
V
s
3
+ a
2
s
2
+ a
1
s + a
0
.
Man w
¨
ahlt drei reelle Pole s
1
= s
2
= s
3
= −λ mit λ>0 und erh
¨
alt
mit V = λ
3
die
¨
Ubertragungsfunktion
G(s)=
λ
3
s
3
+3λs
2
+3λ
2
s + λ
3
.
188 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
V(x)=
λ
3
α
1
+2α
2
|x
3
|
˙x =
2
4
x
2
α
1
x
3
+ α
2
x
3
|x
3
|
0
3
5
+
2
4
0
0
1
3
5
u
y = x
1
r(x)=
3λ(α
1
x
3
+α
2
x
3
|x
3
|)+3λ
2
x
2
+λ
3
x
1
α
1
+2α
2
|x
3
|
w
y
u
r(x)
x
Bild 4.11: Regelung des aktiven Magnetlagers mittels exakter Linearisierung.
Schritt 5: F
¨
ur den Regler gilt mit den Ergebnissen der Schritte 1, 2 und 4:
r(x)=
L
3
a
c(x)+a
2
L
2
a
c(x)+a
1
L
a
c(x)+a
0
c(x)
L
b
L
2
a
c(x)
=
3λ(α
1
x
3
+ α
2
x
3
|x
3
|)+3λ
2
x
2
+ λ
3
x
1
α
1
+2α
2
|x
3
|
.
Schritt 6: F
¨
ur das Vorfilter erh
¨
alt man
v(x)=
V
L
b
L
2
a
c(x)
=
λ
3
α
1
+2α
2
|x
3
|
.
Der so ermittelte Regelkreis ist in Bild 4.11 dargestellt. Mittels des noch
nicht spezifizierten dreifachen Pols bei λ kann die Dynamik des Regelkrei-
ses und insbesondere sein Stellgr
¨
oßenverbrauch beeinflusst werden. So ist es
m
¨
oglich, den Stellgr
¨
oßenverbrauch u innerhalb vorgeschriebener Grenzen, z. B.
−1 ≤ u ≤ 1, zu halten [90, 127, 142].
4.2.4 Regelstrecken mit interner Dynamik
Im Weiteren wollen wir den Fall
δ<n
betrachten, also den Fall, in dem der relative Grad δ gegen
¨
uber der System-
ordnung n reduziert ist. Auch in diesem Fall kann mittels einer nichtlinearen
Transformationsvorschrift, eines Diffeomorphismus z = t(x), eine f
¨
ur den
Reglerentwurf g
¨
unstige Systemdarstellung gefunden werden.
Da δ<ngilt, k
¨
onnen nur die ersten δ Komponenten t
1
, ..., t
δ
in gleicher
Form angesetzt werden wie im Fall δ = n. Es gilt

4.2. Reglerentwurf mittels exakter Linearisierung 189
z =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
z
1
z
2
.
.
.
z
δ
z
δ+1
.
.
.
z
n
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
= t(x)=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
c(x)
L
a
c(x)
.
.
.
L
δ−1
a
c(x)
t
δ+1
(x)
.
.
.
t
n
(x)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
. (4.28)
Die Funktionen t
δ+1
,...,t
n
k
¨
onnen beliebig gew
¨
ahlt werden. Dabei ist aller-
dings die Einschr
¨
ankung zu machen, dass t stetig differenzierbar sein muss
und die Umkehrfunktion
x = t
−1
(z)
existieren und ebenfalls stetig differenzierbar sein muss. Es sei angemerkt,
dass die Umkehrfunktion t
−1
gem
¨
aß dem Hauptsatz
¨
uber implizite Funktionen
[175] existiert, wenn die Jacobi-Matrix ∂t(x)/∂x nicht singul
¨
ar ist.
Transformiert man dann die urspr
¨
ungliche Systembeschreibung
˙x = a(x)+b(x) · u,
y = c(x)
mittels des Diffeomorphismus (4.28), so ergibt sich
˙z =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
˙z
1
˙z
2
.
.
.
˙z
δ−1
˙z
δ
˙z
δ+1
.
.
.
˙z
n
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
d
dt
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
c(x)
L
a
c(x)
.
.
.
L
δ−2
a
c(x)
L
δ−1
a
c(x)
t
δ+1
(x)
.
.
.
t
n
(x)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
L
a
c(x)
L
2
a
c(x)
.
.
.
L
δ−1
a
c(x)
L
δ
a
c(x)+L
b
L
δ−1
a
c(x) · u
˙
t
δ+1
(x)
.
.
.
˙
t
n
(x)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
und somit
˙z =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
˙z
1
˙z
2
.
.
.
˙z
δ−1
˙z
δ
˙z
δ+1
.
.
.
˙z
n
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
z
2
z
3
.
.
.
z
δ
L
δ
a
c(x)+L
b
L
δ−1
a
c(x) · u
˙
t
δ+1
(x)
.
.
.
˙
t
n
(x)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
, (4.29)

190 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
wobei weiterhin
y = z
1
gilt.
Mit
x = t
−1
(z)
bestimmt man f
¨
ur i = δ +1,...,n die Ableitungen
˙
t
i
(x)=
∂t
i
(x)
∂x
˙x =
∂t
i
(x)
∂x
a(x)+b(x) · u
= L
a
t
i
(x)+L
b
t
i
(x) · u (4.30)
=ˆq
i
(x,u)=ˆq
i
(t
−1
(z),u)=q
i
(z,u).
Hat man die Funktion t
i
so gew
¨
ahlt, dass
L
b
t
i
(x)=
∂t
i
(x)
∂x
b(x) = 0 (4.31)
ist, dann vereinfacht sich Gl. (4.30). Denn in diesem Fall entf
¨
allt die Abh
¨
angig-
keit von u, und es gilt
˙
t
i
(x)=L
a
t
i
(x)=ˆq
i
(x)=q
i
(z). (4.32)
Durch den Wegfall der Abh
¨
angigkeit von u vereinfacht sich dann die transfor-
mierte Systemdarstellung wesentlich.
Gleichung (4.31) ist eine partielle Differenzialgleichung, deren L
¨
osung t
i
(x)
in der Regel existiert, aber in vielen F
¨
allen schwierig zu bestimmen ist. Im
Weiteren wollen wir – aus dem genannten Grund der Vereinfachung – davon
ausgehen, dass t
i
die Gleichung (4.31) f
¨
ur alle i = δ +1,...,n erf
¨
ullt und
setzen die Funktionen
˙
t
i
aus Gl. (4.32) in Gl. (4.29) ein. Wir erhalten dann
die so genannte Byrnes-Isidori-Normalform
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
˙z
1
.
.
.
˙z
δ−1
˙z
δ
˙z
δ+1
.
.
.
˙z
n
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
z
2
.
.
.
z
δ
ϕ(z,u)
q
δ+1
(z)
.
.
.
q
n
(z)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
y = z
1
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
externe Dynamik
⎫
⎪
⎬
⎪
⎭
interne Dynamik
0
Ausgangsgr
¨
oße
(4.33)
als Systembeschreibung mit
ϕ(z,u)=L
δ
a
c(t
−1
(z)) + L
b
L
δ−1
a
c(t
−1
(z)) · u.

4.2. Reglerentwurf mittels exakter Linearisierung 191
Die Systemdynamik l
¨
asst sich, wie in Gl. (4.33) dargestellt, in einen exter-
nen und einen internen Anteil aufspalten. Die externe Dynamik des Systems,
die die
¨
Anderungen der Zust
¨
ande z
1
,...,z
δ
beschreibt, kann mittels einer
Transformation der Eingangsgr
¨
oße u in die neue Eingangsgr
¨
oße w, wie im
Fall δ = n, linearisiert werden. Anhand von Gl. (4.29) bzw. (4.33) ermitteln
wir diese Transformation zu
u = −
L
δ
a
c(x)+k
T
z
L
b
L
δ−1
a
c(x)
+
V
L
b
L
δ−1
a
c(x)
· w (4.34)
mit
k
T
=[a
0
··· a
δ−1
0 ··· 0].
Setzt man dies in Gl. (4.33) ein, so erh
¨
alt man die Dynamikgleichungen des
transformierten Systems zu
⎡
⎢
⎢
⎢
⎢
⎢
⎣
˙z
1
˙z
2
.
.
.
˙z
δ−1
˙z
δ
⎤
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
010··· 0
001··· 0
.
.
.
.
.
.
.
.
.
.
.
.
000··· 1
−a
0
−a
1
−a
2
···−a
δ−1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎢
⎢
⎣
z
1
z
2
.
.
.
z
δ−1
z
δ
⎤
⎥
⎥
⎥
⎥
⎥
⎦
+
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0
0
.
.
.
0
V
⎤
⎥
⎥
⎥
⎥
⎥
⎦
w
externe Dynamik
, (4.35)
⎡
⎢
⎣
˙z
δ+1
.
.
.
˙z
n
⎤
⎥
⎦
=
⎡
⎢
⎣
q
δ+1
(z)
.
.
.
q
n
(z)
⎤
⎥
⎦
interne Dynamik
, (4.36)
y = z
1
.
Durch die Transformation (4.34) der Eingangsgr
¨
oße ist die externe Dy-
namik von den Zustandsvariablen z
δ+1
,...,z
n
der internen Dynamik un-
abh
¨
angig. Insbesondere haben die Zustandsvariablen der internen Dynamik
keinen Einfluss auf die Ausgangsgr
¨
oße y. Das hat zur Folge, dass die interne
Dynamik (4.36) nicht beobachtbar ist. Aus dieser Eigenschaft leitet sich auch
die Bezeichnung interne Dynamik ab.
Auch hier interpretieren wir die Transformationsgleichung (4.34) als Re-
gelgesetz, das im ersten Summanden einen Zustandsregler und im zweiten ein
Vorfilter f
¨
ur die F
¨
uhrungsgr
¨
oße w besitzt. Um Gl. (4.34) unabh
¨
angig vom
k
¨
unstlichen Zustandsvektor z zu machen, bilden wir
k
T
z = a
δ−1
L
δ−1
a
c(x)+...+ a
1
L
a
c(x)+a
0
c(x).
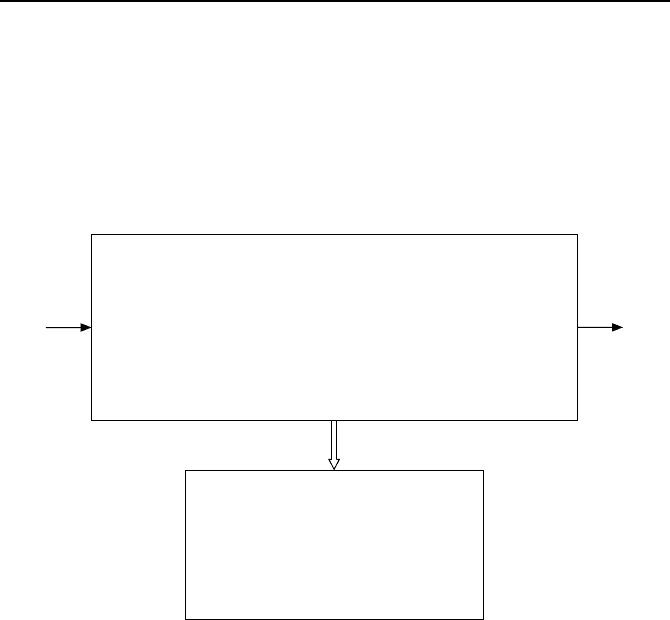
192 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
Offensichtlich kann die interne Dynamik nicht linearisiert werden. Gl
¨
uck-
licherweise beeinflusst sie, wie schon festgestellt, die Ausgangsgr
¨
oße y = z
1
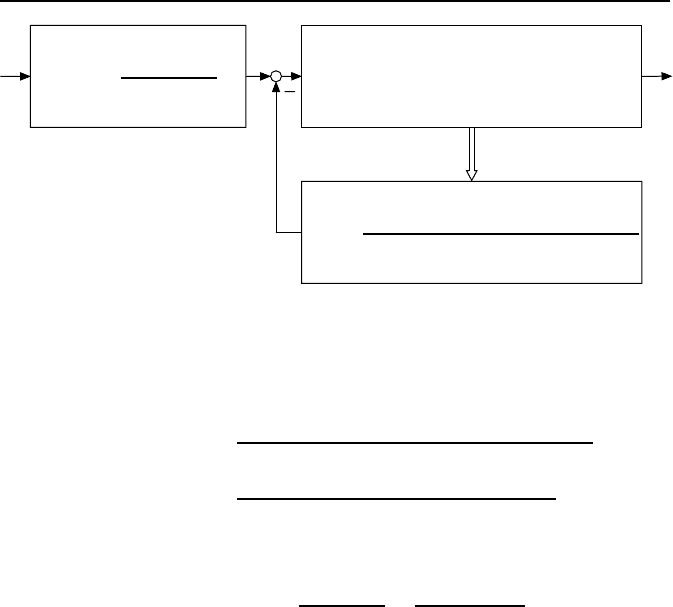
und die geregelte externe Dynamik nicht. Bild 4.12 illustriert dies. Wie er-
w
¨
ahnt, wird die interne Dynamik (4.36) durch das Regelgesetz (4.34) nicht
beobachtbar. Man verursacht durch die Linearisierung des Regelkreises also
seine Nichtbeobachtbarkeit.
Regelkreis mit geregelter externer Dynamik
interne Dynamik
w
y
ˆ
z
1
··· z
δ
˜
2
6
6
6
4
˙z
1
˙z
2
.
.
.
˙z
δ
3
7
7
7
5
=
2
6
6
6
4
010··· 0
001··· 0
.
.
.
.
.
.
.
.
.
.
.
.
−a
0
−a
1
−a
2
··· −a
δ−1
3
7
7
7
5
2
6
6
6
4
z
1
z
2
.
.
.
z
δ
3
7
7
7
5
+
2
6
6
6
4
0
0
.
.
.
V
3
7
7
7
5
w
y = z
1
2
6
4
˙z
δ+1
.
.
.
˙z
n
3
7
5
=
2
6
4
q
δ+1
(z
1
,...,z
n
)
.
.
.
q
n
(z
1
,...,z
n
)
3
7
5
Bild 4.12: Strukturbild des Regelkreises mit geregelter externer Dynamik und nicht
beobachtbarer interner Dynamik.
Die geregelte externe Dynamik, d. h. der Regelkreis (4.35) an sich, besitzt
dabei dieselbe Struktur wie im Fall δ = n, d. h., wie in Bild 4.9 gezeigt. Die
Ausgangsgr
¨
oße ist hier
¨
ahnlich wie im Fall δ = n durch eine lineare Differen-
zialgleichung
y
(δ)
+ a
δ−1
y
(δ−1)
+ ...+ a
1
˙y + a
0
y = V · w
gegeben. Allerdings mit der Ordnung δ<n.
An dieser Stelle wird eine weitere Bedeutung des relativen Grades δ f
¨
ur
das Regelkreisverhalten deutlich. Er legt die Ordnung der linearen Differenzi-
algleichung des Regelkreises fest.
F
¨
ur die Dynamik des linearen Regelkreises spielt die interne Dynamik
zwar keine Rolle, f
¨
ur die Dynamik des Gesamtsystems allerdings schon. Es ist
offensichtlich, dass eine instabile interne Dynamik auch zu einem instabilen
Gesamtsystem f
¨
uhrt. Man muss im Fall δ<nbez
¨
uglich der Stabilit
¨
at des

4.2. Reglerentwurf mittels exakter Linearisierung 193
Gesamtsystems also auch die interne Dynamik beachten. Auch sie muss stabil
sein, damit es das Gesamtsystem ist.
Wir fassen wieder alle Ergebnisse in einem Satz zusammen.
Satz 19 (Exakte Linearisierung bei reduziertem relativen Grad).
Betrachtet wird der Regelkreis
˙x = a(x)+b(x) · u,
y = c(x),
u = −r(x)+v(x) · w
mit dem relativen Grad δ<n. Hat dann der Regler die Form
r(x)=
L
δ
a
c(x)+a
δ−1
L
δ−1
a
c(x)+...+ a
1
L
a
c(x)+a
0
c(x)
L
b
L
δ−1
a
c(x)
und ist das Vorfilter durch
v(x)=
V
L
b
L
δ−1
a
c(x)
,V∈ IR,
mit
L
b
L
δ−1
a
c(x) =0
gegeben, so hat der Regelkreis das lineare
¨
Ubertragungsverhalten
y
(δ)
+ a
δ−1
y
(δ−1)
+ ...+ a
1
˙y + a
0
y = V · w.
Des Weiteren besitzt der Regelkreis die interne Dynamik
⎡
⎢
⎣
˙z
δ+1
.
.
.
˙z
n
⎤
⎥
⎦
=
⎡
⎢
⎣
q
δ+1
(z)
.
.
.
q
n
(z)
⎤
⎥
⎦
mit
z = t(x).
Die interne Dynamik beeinflusst die Ausgangsgr
¨
oße y nicht. Wenn sowohl die
interne als auch die lineare Dynamik der geregelten Ausgangsgr
¨
oße y stabil
sind, dann und nur dann ist das Gesamtsystem stabil.
Satz 18 und Satz 19 sind sehr
¨
ahnlich und unterscheiden sich nur durch die
Ber
¨
ucksichtigung der internen Dynamik in Satz 19. Es ist wichtig anzumerken,
dass zwar der Regelkreis die nicht beobachtbare interne Dynamik besitzt, dass
aber die Regelstrecke normalerweise beobachtbar ist. Daher kann auch der f
¨
ur
die Regelung ben
¨
otigte Zustandsvektor x mittels eines Beobachters gesch
¨
atzt
werden.
Im linearen
¨
Ubertragungsverhalten des Regelkreises

194 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
G(s)=
V
s
δ
+ a
δ−1
s
δ−1
+ ...+ a
1
s + a
0
sind die Koeffizienten a
δ−1
,...,a
1
,a
0
und V f
¨
ur beide F
¨
alle, δ = n wie auch
δ<n,freiw
¨
ahlbar. Die Dynamik des Regelkreises kann also auch hier mittels
der Parameter a
0
,...,a
δ−1
und V beliebig vorgegeben werden. In der Praxis
begrenzt allerdings wieder die Beschr
¨
ankung der Stellgr
¨
oße, |u|≤u
max
,den
dabei zur Verf
¨
ugung stehenden Spielraum.
4.2.5 Entwurfsverfahren
Folgendes allgemeine Schema, das f
¨
ur δ = n wie auch f
¨
ur δ<ngilt, beschreibt
wie der Entwurf von Regler und Vorfilter durchgef
¨
uhrt wird. F
¨
ur den speziel-
len Fall des Magnetlagers in Abschnitt 4.2.3 haben wir ein
¨
ahnliches Schema
schon genutzt.
Schritt 1: Man bestimmt die Terme
L
i
a
c(x),i=0,...,n=dimx.
Schritt 2: Man bestimmt die Terme
L
b
L
i
a
c(x)=
∂L
i
a
c(x)
∂x
b(x) (4.37)
mit i =0, 1, 2,... in aufsteigender Reihenfolge. Der kleinste Index
i,f
¨
ur den obiger Term (4.37) ungleich null ist, liefert die Differenz-
ordnung
δ = i +1.
Der zugeh
¨
orige Term in Gl. (4.37) lautet
L
b
L
δ−1
a
c(x)=
∂L
δ−1
a
c(x)
∂x
b(x) =0.
Schritt 3: Es muss f
¨
ur alle auftretenden x
L
b
L
δ−1
a
c(x) =0
gelten.
Schritt 4: Man w
¨
ahlt die lineare Dynamik des Regelkreises
G(s)=
V
s
δ
+ a
δ−1
s
δ−1
+ ...+ a
1
s + a
0
durch geeignete Festlegung der frei w
¨
ahlbaren Parameter V und
a
δ−1
,...,a
1
,a
0
.

4.2. Reglerentwurf mittels exakter Linearisierung 195
Schritt 5: Man bestimmt mittels der Ergebnisse aus den Schritten 1, 2 und 4
den Regler
r(x)=
L
δ
a
c(x)+a
δ−1
L
δ−1
a
c(x)+...+ a
0
c(x)
L
b
L
δ−1
a
c(x)
.
Schritt 6: Man bestimmt das Vorfilter
v(x)=
V
L
b
L
δ−1
a
c(x)
.
Schritt 7: F
¨
ur δ<nist zu testen, ob die interne Dynamik stabil ist.
Mit obigem Schema ermittelt man nur den Regler r(x) und das Vorfilter
v(x), jedoch nicht die interne Dynamik. Um sie zu erhalten, muss man noch
Gl. (4.29) bzw. Gl. (4.33) aufstellen.
4.2.6 Beispiel Mondlandef
¨
ahre
Wir betrachten im Weiteren ein Beispiel mit interner Dynamik. Es handelt
sich um eine Landef
¨
ahre [131], wie sie z. B. das Landemodul Eagle der Apollo
11 Mission [9, 139], die Marssonde Phoenix oder die Altair-Mondlandef
¨
ahre
des Constellation-Programms der NASA darstellen. Auch das Landemodul
einer m
¨
oglichen bemannten Mars-Mission k
¨
onnte
¨
ahnlich aufgebaut sein. Bild
4.13 zeigt die Mondlandef
¨
ahre Eagle.
Ziel einer Antriebsregelung f
¨
ur eine Raumf
¨
ahre obigen Typs ist vor allem
die Sicherstellung einer weichen Landung. Zu diesem Zweck wird die senkrecht
wirkende Schubkraft des Triebwerks benutzt, um die durch die Gravitation
bedingte Ann
¨
aherung an die Mondoberfl
¨
ache abzubremsen.
Hierbei beschreibt
m
¨
h = −v ˙m − mg (4.38)
die Kr
¨
aftebilanz. Dabei ist m die Masse der F
¨
ahre einschließlich des Treib-
stoffvorrates, h die Flugh
¨
ohe, v die Geschwindigkeit des aus dem Triebwerk
austretenden Gases und g =1.62 m s
−2
ist die Fallbeschleunigung des Mon-
des. Der Term v ˙m repr
¨
asentiert die Schubkraft des Antriebs, wobei ˙m<0
gilt, da die Treibstoffmasse w
¨
ahrend der Landung abnimmt. Der Eagle stand
in der Landephase eine Schubkraft von 4.56 ...45.04 kN zur Verf
¨
ugung. Die
Austrittsgeschwindigkeit betrug v = 3050 m s
−1
.
Zu ber
¨
ucksichtigen ist des Weiteren, dass die Masse des Treibstoffes einen
erheblichen Anteil der Gesamtmasse m ausmacht. So betrug das Gesamtge-
wicht der Eagle m =15.264 kg, wovon 8.165 kg Treibstoff allein f
¨
ur die Lan-
dephase vorhanden waren. Die Abnahme der Masse m durch den Verbrauch
des Treibstoffvorrates ist also f
¨
ur die Bewegungsgleichung (4.38) der F
¨
ahre
ein wesentlicher Gesichtspunkt.
