J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.

3.4. S
¨
attigungsregler 155
−5
schaltende Regelung
lineare Regelung
zeitoptimale Steuerung
Zeit t in s
20
10
10
0
0
0
0
-10
100
100
50
-50
-100
-100
0
0
0
0
5
5
5
5
5
10
10
10
10
15
15
15
15
20
20
20
20
25
25
25
25
30
30
30
30
35
35
35
35
Strom u in A
Kraft x
5
in kN
Winkel x
3
in Grad
Position x
1
in m
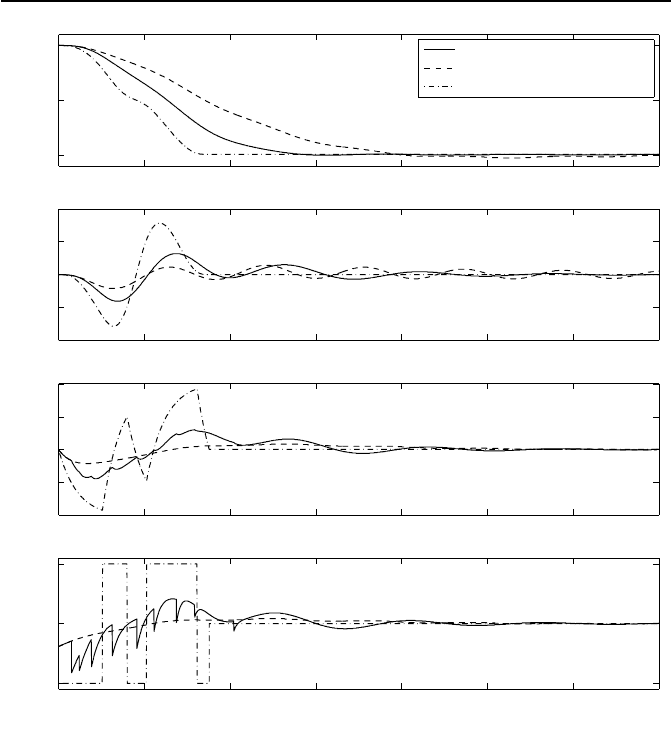
Bild 3.37: Verl
¨
aufe der Position x
1
, des Pendelwinkels x
3
,derAntriebskraftx
5
und
der Stellgr
¨
oße u, d. h. des Motorstromes.
3.4 S
¨
attigungsregler
3.4.1 Funktionsweise und Stabilit
¨
at
Wir betrachten wieder eine lineare Regelstrecke
˙x = Ax + bu
mit der Stellgr
¨
oßenbeschr
¨
ankung
|u|≤u
max
. (3.31)

156 Kapitel 3. Regelungen f
¨
ur lineare Regelstrecken
x
u
˙
x = Ax + bu
k
T
x
Bild 3.38: Regelkreis mit S
¨
attigungsregler u = −sat(k
T
x).
Als Regler verwenden wir einen Zustandsregler −k
T
x, dem es erlaubt ist, die
Begrenzung (3.31) zu verletzen. Es liegt also das Regelgesetz
u =sat(−k
T
x)=
⎧
⎪
⎨
⎪
⎩
u
max
, −k
T
x >u
max
,
−k
T
x, −u
max
≤−k
T
x ≤ u
max
,
−u
max
, −k
T
x < −u
max
(3.32)
vor. Bild 3.38 zeigt die Struktur des Regelkreises. Es zeigt sich, dass man mit
dieser einfachen nichtlinearen Reglerstruktur nicht nur die Stabilit
¨
at des Re-
gelkreises sicherstellen, sondern auch eine schnelle Ausregelung erzielen kann.
Hierbei ist ein Gebiet X
0
von m
¨
oglichen Anfangsauslenkungen x(0) vorge-
geben. Alle diese Anfangsauslenkungen sollen stabil in die Ruhelage x
R
= 0
ausgeregelt werden. Bei instabilen Regelstrecken ist diese Ausregelung nicht
f
¨
ur jedes Gebiet X
0
m
¨
oglich. Der Grund hierf
¨
ur ist die Stellgr
¨
oßenbeschr
¨
an-
kung. Ist u
max
zu klein oder X
0
zu groß, so reicht f
¨
ur große Anfangsauslen-
kungen x(0) die zur Verf
¨
ugung stehende Stellgr
¨
oße u
max
nicht aus, um die
in x(0) startende Trajektorie x(t) in die Ruhelage x
R
= 0 auszuregeln. Das
Gebiet X
0
soll in einem ellipsoidf
¨
ormigen Ljapunov-Gebiet
G =
&
x ∈ IR
n
| x
T
Rx<c
'
liegen, d. h. in einem Gebiet, aus dem keine Trajektorie herausl
¨
auft. Die
Matrix R, die dieses Gebiet festlegt, werden wir im Verlaufe der Stabi-
lit
¨
atsuntersuchung noch bestimmen.
Wir formen nun f
¨
ur die Stabilit
¨
atsuntersuchung das Regelgesetz (3.32) in
die Gestalt
u = −sat(k
T
x)=−h
T
x − p(k
T
x − h
T
x) (3.33)
mit
p =
sat(k
T
x) − h
T
x
k
T
x − h
T
x
(3.34)
3.4. S
¨
attigungsregler 157
um. Dabei ist h so ausgelegt, dass das Ljapunov-Gebiet G Teilmenge des
Gebietes
Z
h
= {x ∈ IR
n
||h
T
x|≤u
max
}
ist. Die zwei Hyberebenen −h
T
x = ±u
max
k
¨
onnen dabei die Ellipse G tan-
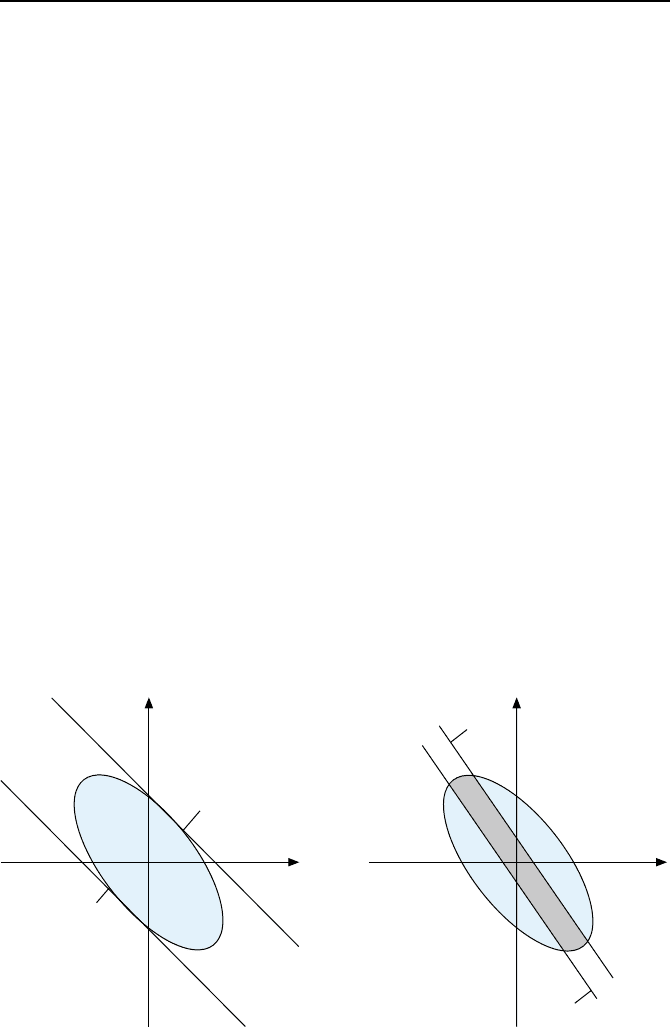
gieren, sollen das Gebiet G aber nicht schneiden. Bild 3.39 illustriert die Si-
tuation.
Der Reglervektor k wird so gew
¨
ahlt, dass er zu einer deutlich schnelle-
ren Ausregelung f
¨
uhrt als der Reglervektor h.Entsprechendgr
¨
oßer ist sein
Stellgr
¨
oßenbedarf und das Gebiet
Z
k
=
/
x ∈ IR
n
||k
T
x|≤u
max
0
zerschneidet das Ljapunov-Gebiet G, so wie es Bild 3.40 zeigt.
Wir betrachten nun alle Zustandsvektoren x ∈ G. Diese wollen wir stabil
mittels Gl. (3.32) bzw. (3.33) nach x = 0 ausregeln. Dabei treten verschiedene
F
¨
alle auf, von denen wir zuerst den betrachten, bei dem
x ∈ Z
k
und x ∈ G
gilt. D. h., der Zustand x befindet sich in der grau dargestellten Zone des
Bildes 3.40. Offensichtlich gelten f
¨
ur solche Vektoren x die Ungleichungen
|h
T
x|≤u
max
und |k
T
x|≤u
max
,
so dass hier mit sat(k
T
x)=k
T
x f
¨
ur den Faktor p aus Gl. (3.34)
x
1
x
2
Z
h
h
T
x = u
max
−h
T
x = u
max
G
Bild 3.39: Gebiet G,GebietZ
h
und
die Hyperebenen |h
T
x| = u
max
.
x
1
x
2
Z
k
−k
T
x =u
max
k
T
x =u
max
G
Bild 3.40: Gebiet G,GebietZ
k
und
die Hyperebenen |k
T
x| = u
max
.

158 Kapitel 3. Regelungen f
¨
ur lineare Regelstrecken
p =
k
T
x − h
T
x
k
T
x − h
T
x
= 1 (3.35)
gilt. Das Regelgesetz (3.33) ist f
¨
ur diese Werte x linear, d. h., es gilt
u = −k
T
x.
Als n
¨
achsten Vektor x, den es auszuregeln gilt, betrachten wir einen be-
liebigen Vektor x,derinG aber nicht in Z
k
liegt. Dieser Bereich G\Z
k
ist
in Bild 3.40 blau dargestellt. F
¨
ur die Zust
¨
ande x ∈ G\Z
k
ist |k
T
x| >u
max
,
d. h., die Regelung befindet sich in S
¨
attigung. Es gilt also
u = −sat(k
T
x)=−u
max
sgn(k
T
x)f
¨
ur x ∈ G\Z
k
und somit ergibt sich in diesem Fall mit
k
T
x = |k
T
x|sgn(k
T
x),
h
T
x = |h
T
x|sgn(h
T
x)
f
¨
ur Gl. (3.34) die Beziehung
p =
u
max
sgn(k
T
x) −|h
T
x|sgn(h
T
x)
|k
T
x|sgn(k
T
x) −|h
T
x|sgn(h
T
x)
.
Wir multiplizieren Z
¨
ahler wie Nenner mit sgn(k
T
x) und erhalten
p =
u
max
−|h
T
x|sgn(h
T
x)sgn(k
T
x)
|k
T
x|−|h
T
x|sgn(h
T
x)sgn(k
T
x)
=
u
max
±|h
T
x|
|k
T
x|±|h
T
x|
f
¨
ur x ∈ G\Z
k
.
Aufgrund dieses Ergebnisses und
|h
T
x|≤u
max
< |k
T
x| f
¨
ur x ∈ G\Z
k
erh
¨
alt man
0 ≤ p<1 (3.36)
f
¨
ur alle x ∈ G\Z
k
. Mit Gl.(3.36) und Gl.(3.35) ergibt sich schließlich
0 ≤ p ≤ 1
f
¨
ur alle x ∈ G.
Um die Stabilit
¨
at des Regelkreises
˙x = Ax − b sat(k
T
x)=
-
A − bh
T
− pb
k
T
− h
T
!.
x

3.4. S
¨
attigungsregler 159
f
¨
ur alle x ∈ G sicherzustellen und um G als Ljapunov-Gebiet auszulegen,
setzen wir
V (x)=x
T
Rx
als Ljapunov-Funktion an. Als zeitliche Ableitung von V erhalten wir
˙
V (x)=x
T
A−bh
T
−pb
k
T
−h
T
!!
T
R+R
A−bh
T
−pb
k
T
−h
T
!!
x < 0.
(3.37)
Offensichtlich ist
˙
V (x)eineinp lineare Funktion, so dass
˙
V (x)seinMaxi-
mum f
¨
ur p ∈ [0, 1] entweder in p =0oderinp = 1 annimmt. Die Bedingung
(3.37) ist also f
¨
ur alle p ∈ [0, 1] erf
¨
ullt, wenn f
¨
ur p =0
x
T
A − bh
T
!
T
R + R
A − bh
T
!
x < 0
und f
¨
ur p =1
x
T
A − bk
T
!
T
R + R
A − bk
T
!
x < 0
gilt. Wir erhalten so folgenden Stabilit
¨
atssatz f
¨
ur die Zustandsregelung mit
S
¨
attigung [76].
Satz 17 (Stabilit
¨
atssatz von Hu und Lin). Der Regelkreis
˙x = Ax − b sat(k
T
x)
besitzt die asymptotisch stabile Ruhelage x
R
= 0 mit dem Einzugsgebiet
G = {x ∈ IR
n
| x
T
Rx<c},
wenn es einen Vektor h gibt, so dass
G ⊆{x ∈ IR
n
||h
T
x|≤u
max
} (3.38)
gilt und die Matrizen
A − bh
T
!
T
R + R
A − bh
T
!
= −Q
h
,
A − bk
T
!
T
R + R
A − bk
T
!
= −Q
k
,
negativ definit sind.
Zu bemerken ist, dass der Reglervektor h im Regelgesetz u = −sat(k
T
x)
keine Rolle spielt. F
¨
ur den Stabilit
¨
atsnachweis im Satz 17 dagegen ist er von
zentraler Bedeutung. Die Bedingung (3.38) ist
¨
aquivalent zur Ungleichung
c · h
T
R
−1
h ≤ u
2
max
.
Diese Ungleichung ist durch Einsetzen von h und R
−1
leicht zu
¨
uberpr
¨
ufen.

160 Kapitel 3. Regelungen f
¨
ur lineare Regelstrecken
3.4.2 Entwurf in mehreren Schritten
Wir wollen uns f
¨
ur den Entwurf eines S
¨
attigungsreglers noch einmal die Ent-
wurfsaufgabe vergegenw
¨
artigen. Der geschlossene Regelkreis besitzt die Ge-
stalt
˙x = Ax − b sat(k
T
x),
wobei ein Reglervektor k gesucht wird, so dass alle Anfangsauslenkungen
x(0) ∈ X
0
stabil in die Ruhelage x
R
= 0 ausgeregelt werden. Das Gebiet
m
¨
oglicher Anfangsauslenkungen X
0
ist dabei oft ein Hyperquader
X
0
= {x ∈ IR
n
|−α
i
≤ x
i
≤ β
i
,i=1,...,n}.
F
¨
ur den Entwurf gehen wir nun in mehreren Schritten vor:
Schritt 1: Bestimme einen Regelvektor h,sodass
˙x =
A − bh
T
!
x
stabil ist.
Schritt 2: Gib eine positiv definite Matrix Q
h
vor und bestimme aus der
Ljapunov-Gleichung
A − bh
T
!
T
R + R
A − bh
T
!
= −Q
h
die Matrix R des Ljapunov-Gebietes G = {x ∈ IR
n
| x
T
Rx<c} .
Schritt 3: Setze
c =
u
2
max
h
T
R
−1
h
.
Dann tangieren die beiden Hyperebenen |h
T
x| = u
max
gerade das
Gebiet G.
Schritt 4: Pr
¨
ufe anhand der Eckpunkte x
ei
von X
0
,obX
0
⊆ G gilt. D. h.,
pr
¨
ufe ob
x
T
ei
Rx
ei
<c
f
¨
ur alle i =1,...,2
n
gilt. Falls dies so ist, fahre mit Schritt 5 fort.
Falls dies nicht gilt, gehe zu Schritt 1 zur
¨
uck und w
¨
ahle einen Regler
h mit geringerem Stellgr
¨
oßenverbrauch oder gehe zu Schritt 2 und
variiere Q
h
.
Schritt 5: W
¨
ahle einen Regelvektor k und
¨
uberpr
¨
ufe, ob die Matrix
A − bk
T
!
T
R + R
A − bk
T
!
= −Q
k
negativ definit ist. Ist dies nicht der Fall, so wiederhole Schritt 5.

3.4. S
¨
attigungsregler 161
Schritt 6: Simuliere den Regelkreis ˙x = Ax − b sat(k
T
x). Ist das Regelver-
halten zufriedenstellend, so beende den Entwurf. Ist es das nicht,
so gehe zu Schritt 1 oder 5 und f
¨
uhre den Entwurf erneut durch.
Der Nachteil des obigen Entwurfsschemas liegt in seinen heuristischen Ent-
wurfsanteilen. So m
¨
ussen die Regelvektoren h und k sowie die Matrix Q
h
auf-
grund von Mutmaßungen gew
¨
ahlt werden. Auch kann nicht von vornherein
sichergestellt werden, ob X
0
⊆ G gilt. Daher m
¨
ussen unter Umst
¨
anden ver-
schiedene Entwurfsschritte mehrfach durchgef
¨
uhrt werden und das Vorgehen
ist dabei durch Versuch und Irrtum gepr
¨
agt.
Das Entwurfsvorgehen mittels obiger f
¨
unf Schritte kann auch auf einem
Rechner implementiert werden und dann automatisiert ablaufen. Des Wei-
teren ist ein Entwurf in einem einzigen Schritt m
¨
oglich [76], wenn alle Ent-
wurfsbedingungen in linearen Matrixungleichungen [25] zusammengefasst wer-
den. Die beschriebenen Nachteile des obigen Entwurfes in sechs Schritten tre-
tendannnichtauf.S
¨
attigungsregler der beschriebenen Art k
¨
onnen auch f
¨
ur
MIMO-Regelstrecken entworfen werden [76].
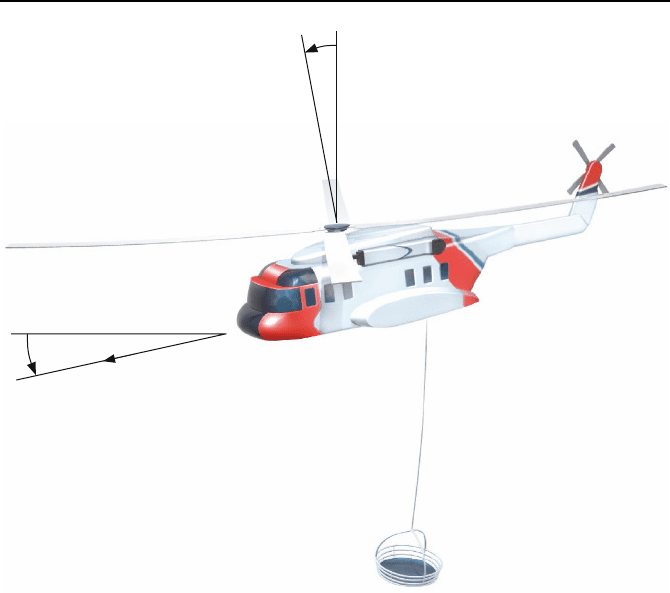
3.4.3 Beispiel Helikopter
Als Beispiel betrachten wir einen Rettungshubschrauber, wie ihn Bild 3.41
zeigt. Der Helikopter soll durch einen Autopiloten konstant
¨
uber einem Ort
gehalten werden k
¨
onnen. D. h., im Fall von Windb
¨
oen und die durch sie ver-
ursachten Positionsabweichungen soll die Regelung des Autopiloten den Heli-
kopter zur
¨
uck auf die konstant zu haltende Position bringen. F
¨
ur Rettungs-
eins
¨
atze bei st
¨
urmischem Wetter ist eine solche Entlastung des Piloten von
großer Bedeutung.
WirbetrachtenhierdiePositionsabweichungx
4
des Helikopters, gemessen
in Metern, in Richtung seiner L
¨
angsachse. Als Teil des Autopiloten wollen wir
diese Positionsabweichung durch eine Regelung bei null halten und sie im Falle
einer St
¨
orung, z. B. durch eine Windb
¨
oe, m
¨
oglichst schnell reduzieren und auf
null zur
¨
uckf
¨
uhren. Die Positionsabweichung l
¨
asst sich mittels des Modells [38]
˙x =
⎡
⎢
⎢
⎣
−0.415 0 −0.0111 0
100 0
−1.43 9.8 −0.0198 0
001 0
⎤
⎥
⎥
⎦
x +
⎡
⎢
⎢
⎣
6.27
0
9.8
0
⎤
⎥
⎥
⎦
u,
y =
0001
x
beschreiben, wobei x
1
die Nickwinkelrate, x
2
der Nickwinkel, x
3
die Geschwin-
digkeit in L
¨
angsrichtung und x
4
die Position bzw., wie erw
¨
ahnt, die Positions-
abweichung ist. Die Stellgr
¨
oße u ist der einstellbare Rotorwinkel, gemessen in
Radiant. Der Rotorwinkel ist durch
−0.11 ≤ u ≤ 0.11
162 Kapitel 3. Regelungen f
¨
ur lineare Regelstrecken
x
2
x
4
u
Bild 3.41: Rettungshubschrauber.
begrenzt. Als Gebiet m
¨
oglicher St
¨
or- bzw. Anfangsauslenkungen betrachten
wir
X
0
=
&
x ∈ IR
4
|x
1
|≤0.1, |x
2
|≤0.2, |x
3
|≤1, |x
4
|≤10
'
.
Wir bestimmen als S
¨
attigungsregler, der den Helikopter f
¨
ur alle St
¨
orauslen-
kungen aus X
0
mit der Stellgr
¨
oßenbeschr
¨
ankung |u|≤0.11 stabil ausregelt,
u = −sat(k
T
x)
mit
k
T
=
0.16226 0.20860 0.0089414 0.0020975
.
F
¨
ur die St
¨
orauslenkung
x
T
0
=
0.10.2110
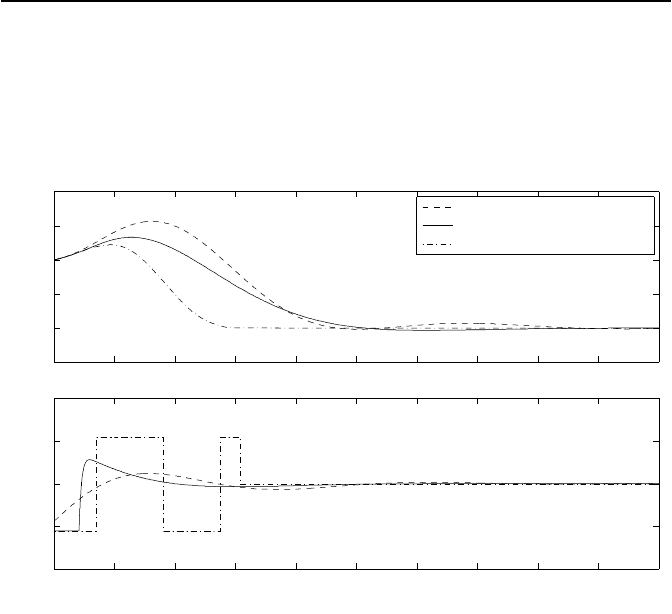
zeigt Bild 3.42 den Verlauf der Ausregelung. Zum Vergleich sind auch die
Verl
¨
aufe eines linearen Reglers u = −k
T
lin
x mit
3.4. S
¨
attigungsregler 163
k
T
lin
=
1.7719 2.8852 0.15954 0.038056
und der zeitoptimalen Steuerung dargestellt. Deutlich zu erkennen ist die ge-
gen
¨
uber dem linearen Regler schnellere Ausregelung des S
¨
attigungsreglers.
Diese wird allerdings durch eine h
¨
ohere Stellgeschwindigkeit ˙u erkauft.
20
15
10
5
-5
0
0
-0.2
-0.1
0.1
0.2
0
0
2
2
4
4
6
6
8
8
10
10
12
12
14
14
16
16
18
18
20
20
Stellgr
¨
oße u in rad
Position y in m
Zeit t in s
lineare Regelung
S
¨
attigungsregelung
zeitoptimale Steuerung
Bild 3.42: Verlauf der Position y und der Stellgr
¨
oße u des Helikopters.

4
Nichtlineare Regelungen f
¨
ur nichtlineare
Regelstrecken
4.1 Gain-scheduling-Regler
4.1.1 Grundlagen
Gain-scheduling-Methoden erm
¨
oglichen es auf Basis der linearen Systemtheo-
rie, relativ einfache und in der Praxis bew
¨
ahrte Regelungen f
¨
ur nichtlinea-
re Regelstrecken zu entwerfen. Aus diesen Gr
¨
unden haben Gain-scheduling-
Regler eine große Verbreitung gefunden. Typische Anwendungen sind Flug-
regelungen, Regelungen in der chemischen Prozessindustrie und Regelungen
in mechatronischen Systemen.
Man linearisiert bei dieser Klasse von Reglern die Regelstrecke f
¨
ur ver-
schiedene Arbeitspunkte. So ergibt sich eine Reihe von linearen Teilmodellen,
f
¨
ur die man jeweils einen Regler entwirft. W
¨
ahrend eines Ausregelvorgangs
aktiviert man den Regler, dessen zugeh
¨
origes Streckenmodell der aktuellen
Situation am besten entspricht, oder interpoliert zwischen den Reglern. Auf
diese Weise wird es m
¨
oglich, die Entwurfsmethoden der linearen Systemtheorie
auf nichtlineare Regelstrecken anzuwenden. Dies kann den Entwurf von Re-
gelungen f
¨
ur nichtlineare Systeme enorm vereinfachen, was sicher ein Grund
f
¨
ur die Beliebtheit dieser Entwurfsmethode ist.
Ausgangsbasis des Gain-schedulings ist die nichtlineare Regelstrecke
˙x = f(x, d, u), x ∈ IR
n
, d ∈ IR
s
, u ∈ IR
m
,
y = g(x), y ∈ IR
r
.
Dabei beschreibt der Vektor d m
¨
ogliche
¨
außere Einflussfaktoren oder St
¨
orgr
¨
o-
ßen. Die Ruhelage bzw. die Ruhelagen x
R
bestimmen sich aus der Gleichung
˙x = f (x
R
, d
R
, u
R
)=0
und h
¨
angen vom Eingangsvektor u
R
der Regelstrecke und eventuell vorhan-
denen
¨
außeren Einflussgr
¨
oßen d
R
ab. Diese Ruhelagen oder Arbeitspunkte
