J?rgen Adamy - Nichtlineare Regelungen
Подождите немного. Документ загружается.

176 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
des Systems, wobei die Variablen
ΔJ = J −J
R
,Δx= x − x
R
,Δu= u − u
R
die Abweichungen von den Ruhelagenwerten darstellen.
Aus Gl. (4.11) und Gl. (4.12) folgt
Δ ˙x = aΔJ − bu
R
Δx −
aJ
R
u
R
Δu,
wobei f
¨
ur den Parametervektor ρ =[u
R
J
R
]
T
gilt.
Wir w
¨
ahlen nun aus den m
¨
oglichen Bereichen der Parameter,
2ls
−1
≤ u
R
≤ 10 l s
−1
und 0 kW m
−2
≤ J
R
≤ 1kWm
−2
,
insgesamt sechs Arbeitspunkte
ρ
i
=
u
Ri
J
Ri
∈
2
4
0.5
,
6
0.5
,
8
0.5
,
4
0.8
,
6
0.8
,
8
0.8
3
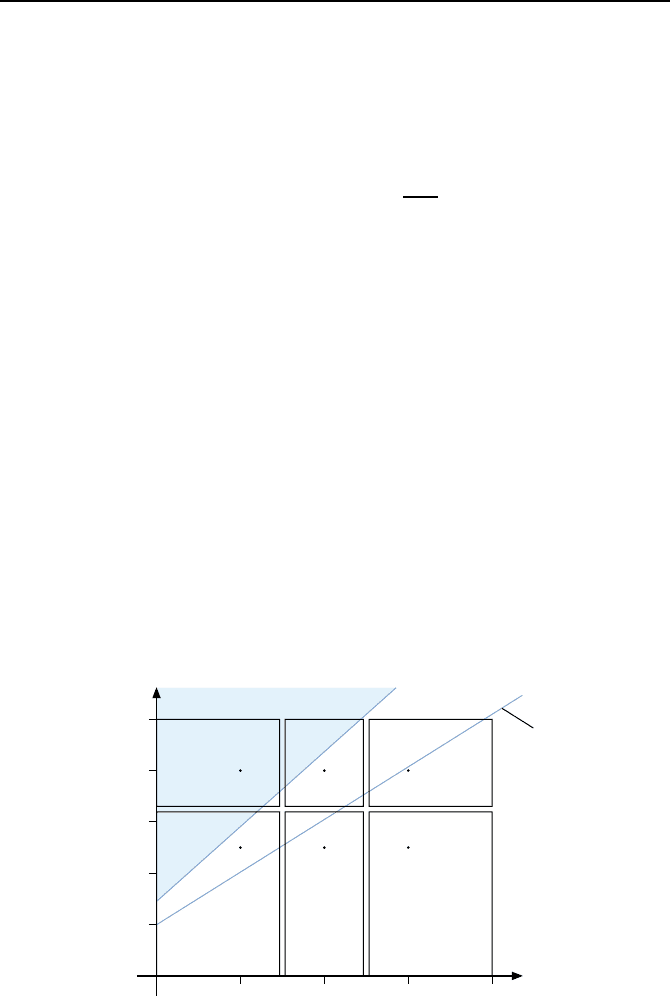
aus. Bild 4.7 illustriert diese Wahl. Dabei liegen im Bereich oberhalb der
Geraden
J
R
=0.1455u
R
,
die sich aus Gl. (4.11) ergibt, Temperaturdifferenzen von ΔT > 100
◦
Cvor.
Dieser Bereich, in dem der Regelkreis nicht betrieben werden darf, ist in Bild
4.7 blau dargestellt. Die je nach St
¨
arke J der Sonneneinstrahlung gew
¨
unschten
station
¨
aren Zust
¨
ande mit x
soll
= ΔT =70
◦
C sind durch die Gerade
4
5
6
123
2
46810
0.2
1
J in kW m
−2
u in l s
−1
ΔT > 100
◦
C
ΔT =70
◦
C
Bild 4.7: Arbeitspunkte (1, 2, 3, 4, 5 und 6) und G
¨
ultigkeitsbereiche der linearen
Teilmodelle, in denen die jeweilige Gauß-Funktion eines Arbeitspunktes dominiert.

4.1. Gain-scheduling-Regler 177
J
R
=0.1019u
R
gegeben.
F
¨
ur die linearen Teilmodelle gilt im i-ten Arbeitspunkt somit
i =1: Δ ˙x
1
=0.58 · ΔJ
1
− 3.39 · 10
−3
· Δx
1
− 73 · 10
−3
· Δu
1
,
i =2: Δ ˙x
2
=0.58 · ΔJ
2
− 5.09 · 10
−3
· Δx
2
− 49 · 10
−3
· Δu
2
,
i =3: Δ ˙x
3
=0.58 · ΔJ
3
− 6.79 · 10
−3
· Δx
3
− 36 · 10
−3
· Δu
3
,
i =4: Δ ˙x
4
=0.58 · ΔJ
4
− 3.39 · 10
−3
· Δx
4
− 117 · 10
−3
· Δu
4
,
i =5: Δ ˙x
5
=0.58 · ΔJ
5
− 5.09 · 10
−3
· Δx
5
− 78 · 10
−3
· Δu
5
,
i =6: Δ ˙x
6
=0.58 · ΔJ
6
− 6.79 · 10
−3
· Δx
6
− 58 · 10
−3
· Δu
6
.
Wir entwerfen f
¨
ur jedes der Teilmodelle einen PI-Regler
Δu
i
= K
i
(x
soll
− x)+K
i
ω
i
t
0
(x
soll
− x) dτ,
mit den jeweiligen Reglerkoeffizienten
K
1
= −1.3254,ω
1
=0.0248,
K
2
= −1.9532,ω
2
=0.0253,
K
3
= −2.5577,ω
3
=0.0257,
K
4
= −0.8284,ω
4
=0.0248,
K
5
= −1.2207,ω
5
=0.0253,
K
6
= −1.5985,ω
6
=0.0257.
Die Regler sind so dimensioniert, dass die geregelten Teilmodelle immer Ei-
genwerte bei
s
1
= −0.04 und s
2
= −0.06
besitzen. Um die Beschr
¨
ankung der Pumpenleistung zu ber
¨
ucksichtigen, be-
sitzen die PI-Regler Antiwindup-Elemente.
Als Schedulingvektor β = ρ verwenden wir
β =
⎡
⎣
u =
aJ
bx
J
⎤
⎦
,
wobei β(t →∞)=ρ gilt. Die Stellgr
¨
oßen u
i
= u
Ri
+ Δu
i
werden
¨
uber die
gewichtete Mittelwertbildung (4.4) zum Gain-scheduling-Regler
u =
6
i=1
e
−||Σ(β−ρ
i
)||
2
u
i
6
i=1
e
−||Σ(β−ρ
i
)||
2
178 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
zusammengefasst. Dabei gilt
Σ =
20
00.3
.
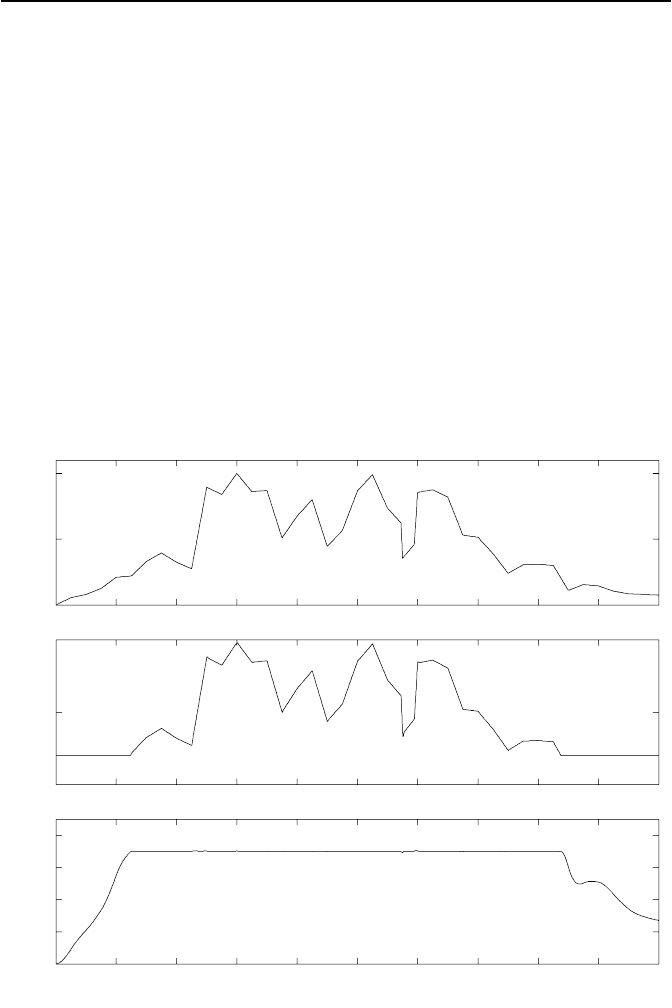
Wir simulieren den Gain-scheduling-Regelkreis des Solarkraftwerkes f
¨
ur
den in Bild 4.8 angenommenen Tagesverlauf der Sonneneinstrahlung. Die
Verl
¨
aufe des Pumpendurchflusses u und der Temperaturdifferenz x = ΔT zwi-
schen Austrittstemperatur und Eintrittstemperatur des
¨
Ols sind ebenfalls in
Bild 4.8 abgebildet. Wie erkennbar, werden die Beschr
¨
ankungen des Pumpen-
durchflusses 2 l s
−1
≤ u ≤ 10 l s
−1
eingehalten. Auch die Temperaturdifferenz
x wird auf dem gew
¨
unschten Wert von x =70
◦
C gehalten. Im Falle einer
Sonneneinstrahlung J von weniger als 0.2kWm
−2
f
¨
allt die Temperaturdif-
ferenz allerdings auf unter 70
◦
C, da dann die Erw
¨
armung des
¨
Ols durch die
Sonne zu gering ist, um bei einem minimal erforderlichen
¨
Olfluss von 2 l s
−1
eine Temperaturdifferenz von 70
◦
C zu erzeugen.
0
0
0
1
1
1
2
2
2
3
3
3
4
4
4
5
5
5
6
6
6
7
7
7
8
8
8
9
9
9
10
10
10
1
0.5
0
0
0
80
60
40
20
10
5
Zeit t in Stunden
x in
◦
C
u in l s
−1
J in kW m
−2
Bild 4.8: St
¨
arke J der Sonneneinstrahlung, Volumenstrom u = q der Pumpe und
Temperaturdifferenz x = ΔT des
¨
Ols zwischen Eintritt und Austritt in das Kollek-
torfeld.

4.2. Reglerentwurf mittels exakter Linearisierung 179
4.2 Reglerentwurf mittels exakter Linearisierung
4.2.1 Grundidee und nichtlineare Regelungsnormalform
In diesem Kapitel soll ein Verfahren betrachtet werden, mit dem es direkt und
nicht
¨
uber den Umweg einer linearen N
¨
aherung der Regelstrecke m
¨
oglich ist,
Regler f
¨
ur nichtlineare Regelstrecken zu entwerfen. Grundgedanke hierbei ist
es, einen nichtlinearen Regler so zu entwerfen, dass er die Nichtlinearit
¨
at der
Regelstrecke kompensiert und insgesamt ein linearer Regelkreis entsteht.
Als Regelstrecken werden SISO-Systeme der Form
˙x = a(x)+b(x) · u,
y = c(x)
betrachtet, also Systeme, die nichtlinear in x, aber linear in u sind. Daher
bezeichnet man sie auch als eingangslineare Systeme oder eingangsaffine Sys-
teme. Die Annahme einer linear wirkenden Stellgr
¨
oße u ist keine große Ein-
schr
¨
ankung, denn viele technische Systeme sind linear in der Stellgr
¨
oße u.
Die Systemordnung ist n =dimx. Die Betrachtung von MIMO-Systemen
ist ohne großen Aufwand und auf
¨
ahnliche Weise wie im SISO-Fall m
¨
oglich
[83, 94, 163, 195]. Wir beschr
¨
anken uns hier nur deshalb auf SISO-Systeme,
um die Grundidee des Verfahrens m
¨
oglichst gut verst
¨
andlich herauszuarbei-
ten.
F
¨
ur den angedachten Reglerentwurf hat sich die Form der obigen System-
beschreibung als ung
¨
unstig herausgestellt. Man muss sie daher geeignet umfor-
men. Zu diesem Zweck verwendet man die Lie-Derivierte oder Lie-Ableitung,
die als Gradient einer skalaren Funktion h(x) multipliziert mit einem Vektor-
feld f(x)definiertist,d.h.als
L
f
h(x)=
∂h(x)
∂x
f(x) = grad
T
h(x) · f(x).
Im vorliegenden Fall gilt z. B.
L
a
c(x)=
∂c(x)
∂x
a(x),
wenn man die Lie-Derivierte auf die Ausgangsfunktion c anwendet.
Man bildet nun die zeitliche Ableitung der Ausgangsgr
¨
oße y und erh
¨
alt
˙y =
dc(x)
dt
=
∂c(x)
∂x
1
˙x
1
+ ...+
∂c(x)
∂x
n
˙x
n
=
∂c(x)
∂x
˙x.
Ersetzt man darin
˙x = a(x)+b(x) · u,
so ergibt sich
˙y =
∂c(x)
∂x
a(x)+
∂c(x)
∂x
b(x) · u
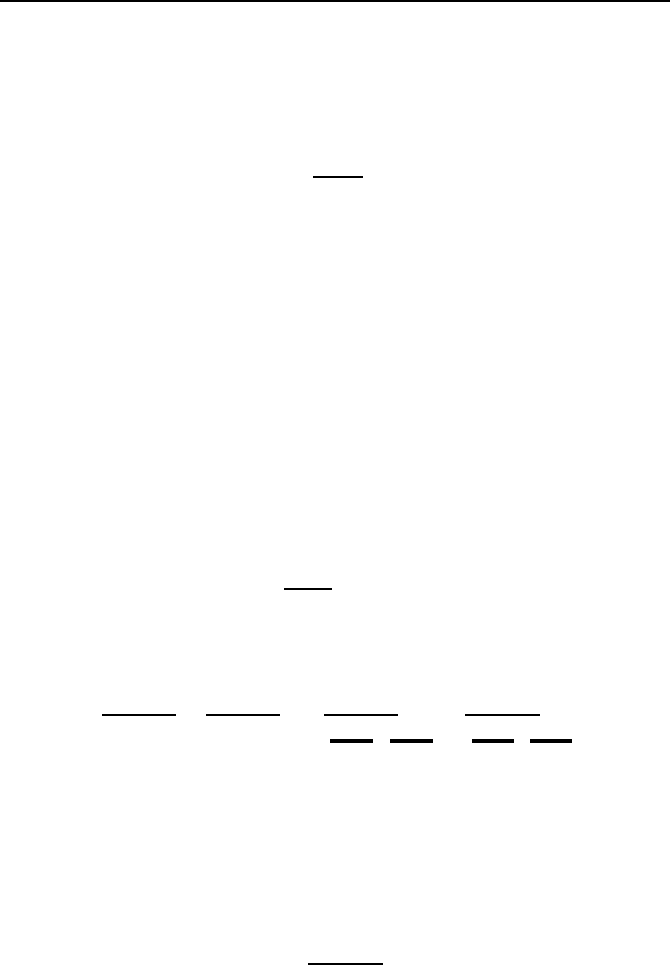
180 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
oder mittels der Lie-Derivierten die Gleichung
˙y = L
a
c(x)+L
b
c(x) · u.
Bei den meisten technischen Systemen ist in der letzten Gleichung
L
b
c(x)=
∂c(x)
∂x
b(x)=0, (4.13)
so dass
˙y = L
a
c(x)
gilt.
Ein Beispiel f
¨
ur Gl. (4.13) liefern lineare Systeme in Regelungsnormalform
˙x = Ax + bu =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
010··· 0
001··· 0
.
.
.
.
.
.
.
.
.
.
.
.
000··· 1
−a
0
−a
1
−a
2
···−a
n−1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
x +
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0
0
.
.
.
0
1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
u,
y = c
T
x =
b
0
b
1
···b
m
0 ···0
x
mit m<n− 1. Bei diesen Systemen gilt offensichtlich
L
b
c(x)=
∂c
T
x
∂x
b(x)=c
T
b =0.
Es soll jetzt ¨y ermittelt werden. Man erh
¨
alt ausgehend von ˙y = L
a
c(x)die
Beziehung
¨y =
dL
a
c(x)
dt
=
∂L
a
c(x)
∂x
˙x =
∂L
a
c(x)
∂x
a(x)
L
a
L
a
c(x)
+
∂L
a
c(x)
∂x
b(x)
L
b
L
a
c(x)
·u.
F
¨
ur den ersten Term in der letzten Gleichung schreibt man abk
¨
urzend
L
a
L
a
c(x)=L
2
a
c(x),
da die Lie-Derivierte L
a
zweimal hintereinander angewandt wird. F
¨
ur den
zweiten Term gilt oftmals wieder
L
b
L
a
(x)=
∂L
a
c(x)
∂x
b(x)=0.
Man erh
¨
alt dann
¨y = L
2
a
c(x).
Bildet man auch die h
¨
oheren Ableitungen, so ergibt sich schließlich folgen-
des Ergebnis:

4.2. Reglerentwurf mittels exakter Linearisierung 181
y = c(x),
˙y = L
a
c(x),
¨y = L
2
a
c(x),
.
.
.
y
(δ−1)
= L
δ−1
a
c(x),
y
(δ)
= L
δ
a
c(x)+
∂L
δ−1
a
c(x)
∂x
b(x) · u. (4.14)
Dabei gilt
L
b
L
i
a
c(x)=
∂L
i
a
c(x)
∂x
b(x)=0
f
¨
ur alle Indizes
i =0,...,δ− 2.
Erst f
¨
ur den Index i = δ − 1wirdL
b
L
δ−1
a
c(x) ungleich null. Man bezeichnet
δ als Differenzordnung oder auch als relativen Grad des Systems. Der relative
Grad entspricht bei linearen Systemen der Differenz zwischen Nennergrad und
Z
¨
ahlergrad der
¨
Ubertragungsfunktion.
Wir betrachten nun zuerst den Fall
δ = n,
also den Fall, bei dem die Systemordnung n =dimx dem relativen Grad δ
entspricht. Dann lassen sich die folgenden neuen Zustandskoordinaten
z =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
z
1
z
2
z
3
.
.
.
z
n
⎤
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
y
˙y
¨y
.
.
.
y
(n−1)
⎤
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
c(x)
L
a
c(x)
L
2
a
c(x)
.
.
.
L
n−1
a
c(x)
⎤
⎥
⎥
⎥
⎥
⎥
⎦
= t(x) (4.15)
einf
¨
uhren. Ist dabei t(x) stetig differenzierbar und existiert die Umkehrfunk-
tion t
−1
, d. h., gilt
t
−1
(t(x)) = x
und ist t
−1
ebenfalls stetig differenzierbar, so nennt man
t : IR
n
→ IR
n
,
wie schon in Abschnitt 1.1.10 beschrieben, einen Diffeomorphismus.Ertrans-
formiert das System
˙x = a(x)+b(x) · u,
y = c(x)

182 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
eineindeutig in die folgende neue Systemdarstellung
⎡
⎢
⎢
⎢
⎣
˙z
1
.
.
.
˙z
n−1
˙z
n
⎤
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎣
z
2
.
.
.
z
n
L
n
a
c(x)
⎤
⎥
⎥
⎥
⎦
+
⎡
⎢
⎢
⎢
⎣
0
.
.
.
0
L
b
L
n−1
a
c(x)
⎤
⎥
⎥
⎥
⎦
u,
y = z
1
.
(4.16)
Diese Systemdarstellung wird als nichtlineare Regelungsnormalform bezeich-
net. Sie l
¨
asst sich unmittelbar aus Gl. (4.14) und Gl. (4.15) herleiten.
Wenn man nun noch die Eingangsgr
¨
oße u transformiert, um sie in Gl.
(4.16) durch eine neue Eingangsgr
¨
oße w gem
¨
aß
u = −
L
n
a
c(x)+k
T
z
L
b
L
n−1
a
c(x)
+
V
L
b
L
n−1
a
c(x)
w (4.17)
mit
k
T
=[a
0
a
1
··· a
n−1
]
zu ersetzen, so ergibt sich das vollst
¨
andig linearisierte System in Regelungs-
normalform
⎡
⎢
⎢
⎢
⎢
⎢
⎣
˙z
1
˙z
2
.
.
.
˙z
n−1
˙z
n
⎤
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
010··· 0
001··· 0
.
.
.
.
.
.
.
.
.
.
.
.
000··· 1
−a
0
−a
1
−a
2
···−a
n−1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎢
⎢
⎣
z
1
z
2
.
.
.
z
n−1
z
n
⎤
⎥
⎥
⎥
⎥
⎥
⎦
+
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0
0
.
.
.
0
V
⎤
⎥
⎥
⎥
⎥
⎥
⎦
w,
y = z
1
.
(4.18)
Mittels der Transformationen (4.15) und (4.17) ist es uns gelungen, die
nichtlineare Systemdarstellung in eine lineare zu
¨
uberf
¨
uhren. Aus dieser Vor-
gehensweise leitet sich der Name exakte Eingangs-/Ausgangslinearisierung,
kurz exakte Linearisierung, ab. In der Wahl der Koeffizienten a
i
im Vektor k
sind wir frei, so dass wir dem transformierten System jede gew
¨
unschte Eigen-
wertkonfiguration einpr
¨
agen k
¨
onnen. Auch der Wert V ist frei w
¨
ahlbar.
4.2.2 Nichtlinearer Regler und linearer Regelkreis
Wir k
¨
onnen die Transformationsvorschrift (4.17) der Eingangsgr
¨
oße u in die
neue Eingangsgr
¨
oße w auch als Regelgesetz
u(x,w)=−r(x)+v(x) · w (4.19)
mit
r(x)=
L
n
a
c(x)+k
T
z
L
b
L
n−1
a
c(x)
(4.20)
4.2. Reglerentwurf mittels exakter Linearisierung 183
u
w
x
y
v(x)
˙x = a(x)+b(x) · u
c(x)
r(x)
Bild 4.9: Strukturbild des Regelkreises mit insgesamt linearer Dynamik.
als Regler und
v(x)=
V
L
b
L
n−1
a
c(x)
als Vorfilter interpretieren. Die Gr
¨
oße w fungiert dabei als F
¨
uhrungsgr
¨
oße des
Regelkreises.
F
¨
ur die Differenzialgleichung der Ausgangsgr
¨
oße y ergibt sich aus Gl. (4.18)
y
(n)
+ a
n−1
y
(n−1)
+ ...+ a
1
˙y + a
0
y = V · w.
Bild 4.9 zeigt das zugeh
¨
orige Strukturbild. Durch die frei w
¨
ahlbaren Parameter
a
i
und V kann die Dynamik des Regelkreises offensichtlich beliebig ausgelegt
werden. In der Praxis begrenzt allerdings die Beschr
¨
ankung der Stellgr
¨
oße,
|u|≤u
max
, die freie Wahl der Parameter a
i
und V .
Um das Regelgesetz (4.19), (4.20) unabh
¨
angig von z zu machen, setzt man
noch
z = t(x)=
⎡
⎢
⎢
⎢
⎣
c(x)
L
a
c(x)
.
.
.
L
n−1
a
c(x)
⎤
⎥
⎥
⎥
⎦
in Gl. (4.20) ein und erh
¨
alt so die nichtlineare Ackermann-Formel
u = −
L
n
a
c(x)+a
n−1
L
n−1
a
c(x)+...+ a
1
L
a
c(x)+a
0
c(x)
L
b
L
n−1
a
c(x)
+
V
L
b
L
n−1
a
c(x)
w
als Regelgesetz, das nur noch vom Originalzustand x abh
¨
angt.
Um alle Ergebnisse zu
¨
uberblicken, fassen wir sie in folgendem Satz zu-
sammen.

184 Kapitel 4. Regelungen f
¨
ur nichtlineare Regelstrecken
Satz 18 (Exakte Linearisierung bei maximalem relativen Grad). Be-
trachtet wird der Regelkreis
˙x = a(x)+b(x) · u,
y = c(x),
u = −r(x)+v(x) · w
mit dem relativen Grad δ = n. Hat dann der Regler die Form
r(x)=
L
n
a
c(x)+a
n−1
L
n−1
a
c(x)+...+ a
1
L
a
c(x)+a
0
c(x)
L
b
L
n−1
a
c(x)
und ist das Vorfilter durch
v(x)=
V
L
b
L
n−1
a
c(x)
,V∈ IR,
mit
L
b
L
n−1
a
c(x) =0
gegeben, so hat der Regelkreis das lineare
¨
Ubertragungsverhalten
y
(n)
+ a
n−1
y
(n−1)
+ ...+ a
1
˙y + a
0
y = V · w.
Wir bezeichnen das Vorgehen in Satz 18 als exakte Linearisierung bei ma-
ximalem relativen Grad, da es auf den h
¨
ochsten m
¨
oglichen Wert δ = n zuge-
schnitten ist. Den Fall δ<nbehandeln wir in Abschnitt 4.2.4.
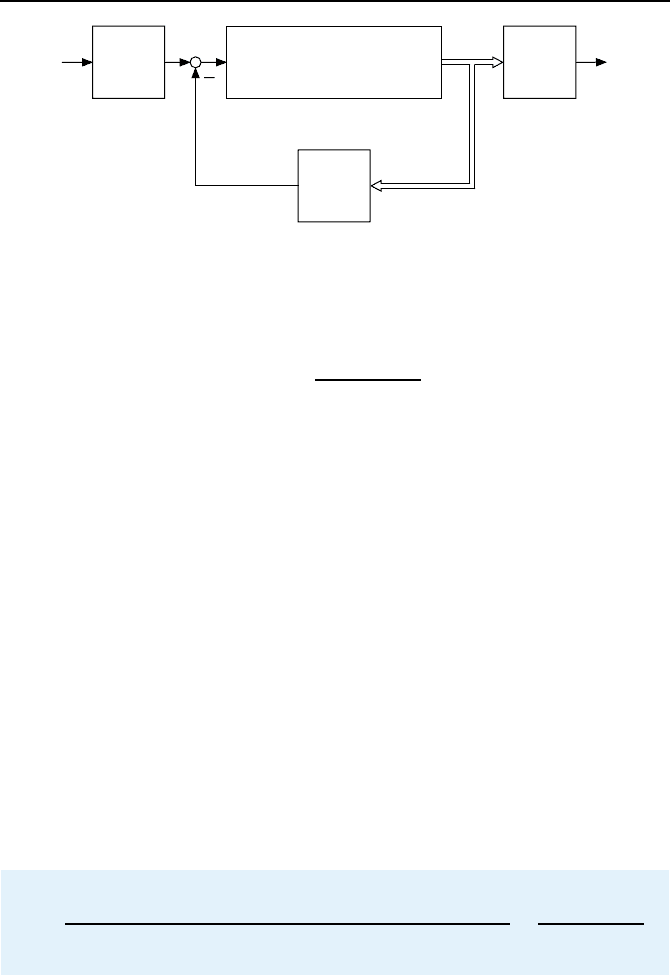
4.2.3 Beispiel Magnetlager
Wir betrachten ein aktives Magnetlager [130, 184], wie es in elektrischen Gene-
ratoren und Motoren, Pumpen und Turbinen eingesetzt wird. Es erm
¨
oglicht
eine reibungsfreie Lagerung der Maschinenwelle und so die Einsparung von
Energie. Das prinzipielle Funktionsschema eines Magnetlagers mit einem Frei-
heitsgrad zeigt Bild 4.10. Die beiden Elektromagneten halten die Welle in der
Position h =0.
Die von den Str
¨
omen i
1
und i
2
verursachten magnetischen Fl
¨
usse Φ
1
und
Φ
2
bewirken dabei die Kr
¨
afte F
1
und F
2
, die auf die Welle wirken. Diese Kr
¨
afte
werden so eingestellt, dass die Lagerung ber
¨
uhrungslos erfolgt. Dabei kann
man, um elektrische Energie einzusparen, die Elektromagneten wechselseitig
ein- bzw. ausschalten. Diese Betriebsart bezeichnet man als Zero-bias-Betrieb
oder Low-bias-Betrieb.
Die auf die Welle wirkenden Kr
¨
afte
F
i
=
1
μ
0
A
Φ
2
i
,i=1, 2, (4.21)

4.2. Reglerentwurf mittels exakter Linearisierung 185
Elektromagnet
R
1
F
1
R
2
F
2
h
i
1
u
1
i
2
u
2
Maschinenwelle
Bild 4.10: Prinzipielles Funktionsschema eines aktiven Magnetlagers mit einem Frei-
heitsgrad in Richtung von h. Weitere, nicht betrachtete Freiheitsgrade sind durch
zus
¨
atzliche Elektromagneten angedeutet.
h
¨
angen variabel vom magnetischen Fluss Φ
i
des jeweiligen Elektromagneten i
ab. Dabei ist μ
0
die magnetische Feldkonstante und A die Fl
¨
ache eines Pols
der Elektromagneten. F
¨
ur den magnetischen Fluss gilt des Weiteren
Φ
i
= Φ
0
+ φ
i
,i=1, 2, (4.22)
wobei Φ
0
φ
i
ist. Der Flussanteil Φ
0
ist konstant, d. h., er bildet einen
Gleichanteil, den Bias. Die Flussanteile φ
i
enthalten die zeitlich ver
¨
anderlichen
Komponenten. F
¨
ur den Zusammenhang zwischen der Spannung u
i
des Elek-
tromagneten i und dem Fluss Φ
i
gilt
˙
Φ
i
=
˙
φ
i
=
u
i
N
,i=1, 2. (4.23)
Dabei ist u
i
die am i-ten Elektromagnet anliegende Spannung und N die
Anzahl der Windungen des Elektromagneten. Man definiert nun
φ = φ
1
− φ
2
(4.24)
