J?rgen Adamy - Nichtlineare Regelungen

Подождите немного. Документ загружается.

94 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

1.33

ReRe

(s)=

s +2

s +1

(s)=

s +4

s +3

Bild 2.56: Ortskurven der beiden Teilsysteme.

ur die Popov’sche Integralungleichung erh

alt man



(τ)y(τ) dτ =



(τ)sat(K

(τ)) + y

(τ)sat(K

(τ))) dτ ≥−ε

Diese Ungleichung ist sicher erf

ullt f

ur alle t ≥ 0, da

sat(K

) ≥ 0

ur alle y

∈ IR und alle K

> 0, i =1, 2, gilt. Der Regelkreis (2.13), (2.16)

besitzt also in x = 0 eine global asymptotisch stabile Ruhelage.

In einem weiteren Beispiel f

ur die Anwendung von Satz 8 betrachten wir

eine Regelstrecke ohne Durchgriﬀ

˙x = Ax + Bu,

y = Cx.

(2.17)

Wir gehen davon aus, dass f

ur sie die Kalman-Jakubovich-Gleichungen

R + RA = −LL

= RB

erf

ullt sind. Uns interessiert nun, welche Regler

u = −v = −K(t) · y (2.18)

zu einem stabilen Regelkreis f

uhren. Um dies herauszuﬁnden, setzen wir das

Regelgesetz (2.18) in die Popov’sche Integralungleichung ein und erhalten



K(τ)y dτ ≥−ε

2.4. Die Stabilit

atstheorie von Ljapunov 95

Hinreichend f

ur die Erf

ullung dieser Ungleichung und damit auch f

ur die

Stabilit

at des Regelkreises (2.17), (2.18) ist die Forderung, dass die Matrix

K(t) positiv semideﬁnit f

ur alle t ≥ 0 ist. Man beachte, dass die Reglermatrix

K(t)auchvonx(t)odery(t)abh

angen darf, d. h. die Form K(x(t)) oder

K(y(t)) aufweisen darf.

2.4 Die Stabilit

atstheorie von Ljapunov

2.4.1 Die Idee und die direkte Methode

In den vorherigen Kapiteln wurden Verfahren zur Stabilit

atsanalyse nichtli-

nearer Regelkreise betrachtet, die bestimmten eingeschr

ankten Systemklassen

zuzuordnen sind. Dies waren u. a. das Verfahren der harmonischen Balance,

das Popov-Kriterium und das Hyperstabilit

atskriterium. F

ur die Regelungs-

technik sind oben genannte Verfahren wichtig, da sie in der Praxis oft vor-

kommende Regelkreisstrukturen behandeln.

Allgemeine Verfahren zur Stabilit

atsanalyse nichtlinearer Systeme sind

diese Verfahren aber leider nicht. Ein solches Verfahren wurde 1892 von A.

M. Ljapunov

[1]

angegeben [117, 118, 119]. Es hat eine Vielzahl von Erweite-

rungen erfahren [12, 64, 66, 157]. Prinzipiell sind mit Ljapunovs Verfahren

alle dynamischen Systeme auf ihre Stabilit

at hin untersuchbar. Es wird sich

allerdings zeigen, dass dies praktisch oft nicht m

oglich ist. Das Verfahren Lja-

punovs l

ost das Problem der Stabilit

atsuntersuchung nichtlinearer Systeme

also auch nicht vollst

andig.

Um die Grundidee Ljapunovs zu skizzieren, betrachtet man verschiedene

alle m

oglichen Stabilit

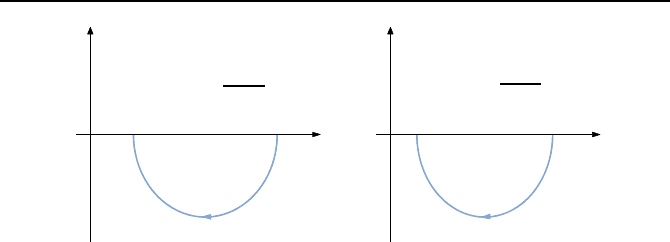
atsverhaltens anhand des Beispiels einer Kugel mit

Reibung unter Einwirkung der Erdbeschleunigung g. Bild 2.57 illustriert ent-

sprechende Anordnungen. Nur die linke weist eine stabile Ruhelage auf.

Bild 2.57: Stabilit

atssituationen einer Kugel im Gravitationsfeld.

[1]

Im Deutschen ist auch die Schreibweise Ljapunow, im Englischen Lyapunov oder

seltener Liapunov gebr

auchlich.

96 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Die potenzielle Energie

= mgy

der Kugel mit der Masse m ist proportional zur H

ohe y. Durch die jeweili-

ge Anordnung ist eine Zwangsbewegung auf einer bestimmten Bahn vorge-

schrieben, so dass die y-Koordinate eine Funktion f von x und z ist. F

ur die

potenzielle Energie gilt also auch

= mgf(x, z).

Oﬀensichtlich ist eine Ruhelage nur stabil, wenn die potenzielle Energie in

der Ruhelage ein Minimum besitzt. D. h., dass im betrachteten Beispiel die

Funktion f ein Minimum besitzen muss.

Dies allein reicht allerdings noch nicht aus, um die Stabilit

at sicherzustel-

len, wie folgende Erweiterung des Beispiels zeigt. Nun soll in der Kugel ein

Antrieb enthalten sein, der dazu f

uhrt, dass sie aufschwingt, wie es Bild 2.58

illustriert. Dann ist die Ruhelage nicht stabil, obwohl die potenzielle Energie

Bild 2.58: Kugel mit Energiequelle und Antrieb zum Aufschwingen.

ein Minimum aufweist. Dies ist darauf zur

uckzuf

uhren, dass das System eine

innere Energiequelle besitzt.

Außer der Forderung, dass die potenzielle Energie ein Minimum besitzt,

ist oﬀensichtlich eine weitere Bedingung n

otig, damit eine Ruhelage stabil ist.

Man fordert daher zus

atzlich, dass die potenzielle Energie entlang aller Tra-

jektorien in der Umgebung der Ruhelage abnimmt oder zumindest konstant

bleibt.

Betrachtet man diese

Uberlegungen genauer, so scheint man sich von der

Ausgangsposition einer potenziellen Energiefunktion l

osen und obige Vorge-

hensweise verallgemeinern zu k

onnen. Es scheint ausreichend zu sein, eine be-

liebige Funktion zu betrachten, die folgende zwei Forderungen erf

ullt, damit

eine Ruhelage stabil ist:

(1) Die Funktion muss in der Ruhelage ein Minimum besitzen.

(2) Die Funktion muss in einer Umgebung der Ruhelage entlang aller Trajek-

torien abnehmen.

2.4. Die Stabilit

atstheorie von Ljapunov 97

Das ist die Grundidee der direkten Methode von Ljapunov,auchzweite Metho-

de genannt. Und A. M. Ljapunov hat den folgenden, f

ur die Stabilit

atsanalyse

dynamischer Systeme zentralen Satz bewiesen.

Satz 9 (Direkte Methode von Ljapunov). Die Diﬀerenzialgleichung

˙x = f(x) mit der Ruhelage x

= 0 besitze f

ur jeden Anfangswert aus einer

Umgebung U

(0) des Ursprungs eine stetige und eindeutige L

osung. Existiert

dann eine Funktion V (x) mit

(1) V (0)=0,

die in einer Umgebung U

(0) ⊆ U

(0) stetig ist, stetige partielle Ableitungen

besitzt und dort mit Ausnahme von x = 0 die Bedingungen

(2) V (x) > 0,

(3)

V (x) ≤ 0(bzw.

V (x) < 0)

erf

ullt, so ist die Ruhelage x

= 0 stabil im Sinne von Ljapunov (bzw. asym-

ptotisch stabil).

Die Bedingungen (1) und (2) stellen sicher, dass V ein Minimum in x = 0

besitzt. Die Bedingung (3) bedeutet, dass V entlang aller Trajektorien aus

(0) mit der Zeit abnimmt oder konstant bleibt. Es sei noch einmal darauf

hingewiesen, dass die Annahme einer Ruhelage in x = 0 keine Einschr

ankung

der Allgemeinheit ist. Denn jede Ruhelage kann, wie in Abschnitt 1.1.3 fest-

gestellt, nach x = 0 transformiert werden.

Satz 9 erm

oglicht es zu

uberpr

ufen, ob eine Ruhelage stabil im Sinne von

Ljapunov oder asymptotisch stabil ist. Abh

angig ist dies davon, ob

V (x) ≤ 0

oder

V (x) < 0 ist. Bild 2.59 illustriert den Fall

V (x) ≤ 0. Im Fall, dass auch

V (x) = 0 gilt, k

onnen Trajektorien x(t), die nicht in die Ruhelage x

= 0

laufen, die Ungleichung

V (x) ≤ 0erf

ullen. D. h., die Ruhelage ist nur stabil

im Sinne von Ljapunov. In Bild 2.60 dagegen ist der Fall der asymptotischen

Stabilit

at dargestellt. Er liegt vor, wenn V (x) entlang aller Trajektorien x(t)

abnimmt, also f

ur die zeitliche Ableitung

V (x) < 0 gilt.

V (x)=c

Bild 2.59: Stabilit

at im Sinne von

Ljapunov.

Bild 2.60: Beispiel f

ur asymptotische

Stabilit

at.

98 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Sind die Bedingungen (2) und (3) im gesamten Zustandsraum erf

ullt und

gilt zus

atzlich

V (x) →∞ f

ur |x|→∞, (2.19)

so ist die Ruhelage global stabil im Sinne von Ljapunov (bzw. global asym-

ptotisch stabil). Eine Funktion mit der Eigenschaft (2.19) bezeichnet man als

radial unbeschr

ankt.

Funktionen V (x), welche die Bedingungen des Stabilit

atssatzes 9 erf

ullen,

nennt man Ljapunov-Funktionen. Praktisch bildet man die Ableitung einer

Ljapunov-Funktion V (x) nach der Zeit mittels des Gradienten

V (x)= ˙x

grad V (x)=



i=1

˙x

∂V

∂x

(2.20)

und setzt die Ableitung des Zustandsvektors

˙x = f(x)

in Gl. (2.20) ein. Dann hat man zu pr

ufen, ob

V (x) ≤ 0bzw.

V (x) < 0f

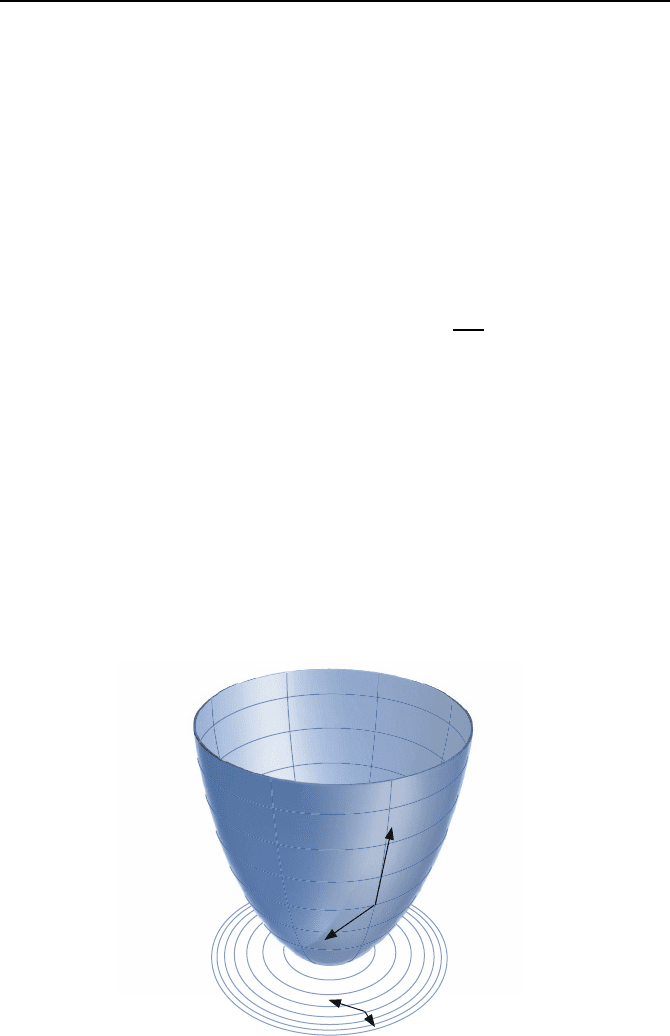
x = 0 gilt. Dies veranschaulicht Bild 2.61. Man ben

otigt bei der Anwendung

von Satz 9 also nicht die L

osung der Diﬀerenzialgleichung, die im Falle nicht-

linearer Systeme oft auch gar nicht analytisch bestimmbar ist. Die direkte

Verwendung der Diﬀerenzialgleichung bei der Berechnung von

V (x)gibtder

Methode ihren Namen.

•

grad V (x)

˙x

Bild 2.61: Veranschaulichung der Gleichung

V (x)= ˙x

grad V (x) < 0.

2.4. Die Stabilit

atstheorie von Ljapunov 99

Wir wollen nun noch den Fall betrachten, dass wir eine Ljapunov-Funktion

V f

ur ein System

x = f (x) kennen, f

ur die wir nur

V (x) ≤ 0 und daher

mit Satz 9 nur Stabilit

at im Sinne von Ljapunov und keine asymptotische

Stabilit

at nachweisen k

onnen. Existiert nun keine Trajektorie x(t), die bei ir-

gendeinem Anfangswert x(0) beginnt und entlang derer die Ableitung

V (x(t))

fortw

ahrend identisch null ist, so nimmt V entlang aller Trajektorien aus der

Umgebung der Ruhelage x

= 0 ab. Folglich ist die asymptotische Stabi-

lit

at der Ruhelage auch in diesem Fall nachweisbar [13]. Wir formulieren dies

aziser in

Satz 10 (Satz von Barbashin und Krasovskii). Die Diﬀerenzialglei-

chung ˙x = f(x) mit der Ruhelage x

= 0 besitze f

ur jeden Anfangswert aus

einer Umgebung U

(0) des Ursprungs eine stetige und eindeutige L

osung. Es

existiere eine Funktion V (x) mit

(1) V (0)=0,

die in einer Umgebung U

(0) ⊆ U

(0) stetig ist, stetige partielle Ableitungen

besitzt und dort mit Ausnahme von x = 0 die folgenden Bedingungen erf

ullt:

(2) V (x) > 0

(3)

V (x) ≤ 0

(4) Die Menge von Zust

anden x,f

ur die

V (x)=0gilt, enth

alt keine Trajek-

torie x(t).

Dann ist die Ruhelage x

= 0 asymptotisch stabil.

Ist die Ljapunov-Funktion des obigen Satzes außerdem noch radial unbe-

schr

ankt und ist U

(0)=IR

, so ist die Ruhelage global asymptotisch stabil.

Satz 10 erweist sich in der Praxis oft als n

utzlich, wenn man nur eine

Ljapunov-Funktion mit

V (x) ≤ 0 ﬁnden kann. Die Bedingung (4) l

asst sich

uberpr

ufen, indem man die Menge der Werte x bestimmt, f

ur die

V (x)=0

ist. Diese Werte setzt man in ˙x = f (x) ein. Enthalten sie eine andere L

osung

der Diﬀerenzialgleichung als x = 0, so ist die Bedingung (4) nicht erf

ullt.

Meistens ist sie allerdings erf

ullt, denn nur in seltenen F

allen verl

auft eine

Tra jektorie x(t)fortw

ahrend auf einer H

ohenlinie der Ljapunov-Funktion V ,

was identisch mit

V (x(t)) = 0 ist.

Das Problem bei der Anwendung obiger Stabilit

atss

atze ist das Auﬃnden

einer Ljapunov-Funktion V (x). F

ur das eine oder andere nichtlineare System,

wie das im nachfolgenden Abschnitt, und f

ur lineare Systeme ist die Ermitt-

lung einer Ljapunov-Funktion aufgrund der Anschauung einfach. Im allgemei-

nen Fall stellt es sich allerdings als außerordentlich problematisch heraus, eine

Ljapunov-Funktion zu bestimmen. Zwar gibt es eine Reihe von Konstruktions-

methoden f

ur Ljapunov-Funktionen [52, 144] wie die Methoden von Aiserman,

die von Schultz und Gibson, die von Ingwerson oder die Methode von Zubow.

Doch sind sie nur auf Spezialf

alle anwendbar und in vielen F

allen aufwendig

zu handhaben. Letztendlich ist man daher in der Mehrzahl der F

alle auf das

Ausprobieren verschiedener Funktionsans

atze f

ur V (x) angewiesen.

100 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

2.4.2 Illustrationsbeispiel

Es folgt ein Beispiel. Und zwar betrachten wir das schon im Abschnitt 1.1.6

behandelte System

˙x

= x

− 1),

˙x

= x

− 1)

mit den Ruhelagen x

= 0 und x

=[1 1]

. Seine Trajektorien zeigt

Bild 2.62. Eine Kandidatin f

ur eine Ljapunov-Funktion zum Nachweis der

Stabilit

at der Ruhelage x

= 0 ist

V (x)=x

+ x

denn es gilt V (0) = 0 und sonst V (x) > 0. Die H

ohenlinien von V haben die

Form von Kreisen. Die Ruhelage x

ist, wir erinnern uns, instabil.

Es ist jetzt zu

uberpr

ufen, ob die Funktion

V (x)=x

+ x

entlang aller Systemtrajektorien x(t)inderN

ahe der Ruhelage abnimmt. Man

bildet zu diesem Zweck

V (x)= ˙x

grad V (x)



˙x







=2x

− 1) + 2x

− 1).

Zustand x

-1

-2

-1

Bild 2.62: Trajektorien x(t) und kreisf

ormige H

ohenlinien (blau) der Ljapunov-

Funktion V (x)=x

+ x

2.4. Die Stabilit

atstheorie von Ljapunov 101

Es gilt

V (x) < 0f

ur x

< 1 und x

< 1,

so dass die Ruhelage

= 0

asymptotisch stabil und

V (x)=x

+ x

eine Ljapunov-Funktion ist. Bild 2.62 illustriert diese Ergebnisse, wobei die

ohenlinien von V (x), wie gesagt, Kreise bilden.

2.4.3 Quadratische Ljapunov-Funktionen

Funktionen mit kreis- oder ellipsoidf

ormigen H

ohenlinien scheinen, aus rein

anschaulichen Motiven heraus, geeignete Kandidatinnen von Ljapunov-Funk-

tionen f

ur verschiedene Systeme zu sein. Ihre allgemeine Form ist durch positiv

deﬁnite quadratische Formen

V (x)=x

gegeben. Bild 2.63 zeigt die H

ohenlinien einer solchen Funktion.

Die Bedingung (1) des Satzes 9,

V (0)=0,

ist ersichtlich erf

ullt, und wenn R eine positiv deﬁnite Matrix ist, ist es auch

die Bedingung (2), d. h.

V (x) > 0f

ur x = 0.

V (x)=const

Bild 2.63: H

ohenlinien einer quadratischen Funktion.

102 Kapitel 2. Grenzzyklen und Stabilit

atskriterien

Es bleibt die

Uberpr

ufung der Bedingung (3), d. h.

V (x) ≤ 0bzw.

V (x) < 0,

ur das jeweils betrachtete System.

Inwieweit sich der Ansatz quadratischer Formen x

Rxf

ur eine Ljapunov-

Funktion als tragf

ahig erweist, soll anhand linearer Systeme

˙x = Ax (2.21)

untersucht werden. Es gilt mit

V (x)=x

V (x) die Gleichung

V (x)=x

R ˙x + ˙x

Rx.

Setzt man Gl. (2.21) hierin ein, so erh

alt man

V (x)=x

RA x + x

= x

RA + A



 

−Q

Fordert man f

ur asymptotische Stabilit

V (x)=−x

Qx< 0,

so muss die Matrix Q positiv deﬁnit sein.

Ergibt sich also aus der Matrixgleichung

R + RA = −Q (2.22)

eine positiv deﬁnite Matrix Q,dannistV (x)=x

Rx eine Ljapunov-Funk-

tion und das System ˙x = Ax asymptotisch stabil. Man kann auch umge-

kehrt vorgehen, eine beliebige positiv deﬁnite Matrix Q vorgeben und – wenn

das System (2.21) stabil ist – eine positiv deﬁnite Matrix R und damit

eine Ljapunov-Funktion bestimmen. Die Gleichung (2.22) heißt Ljapunov-

Gleichung. Es gilt der folgende Satz.

Satz 11 (Ljapunov-Gleichung). Die Ruhelage x

= 0 des linearen Sys-

tems ˙x = Ax ist genau dann asymptotisch stabil, wenn f

ur eine beliebige re-

elle, symmetrische, positiv deﬁnite Matrix Q ein R existiert, so dass

R + RA = −Q

gilt. Die Funktion V = x

Rx ist dann eine Ljapunov-Funktion des Systems.

2.4. Die Stabilit

atstheorie von Ljapunov 103

ur stabile lineare Systeme k

onnen also immer quadratische Ljapunov-

Funktionen gefunden werden. Zumindest in diesem Fall erweist sich der Ansatz

solcher Ljapunov-Funktionen als sehr geeignet.

Satz 11 hat eigentlich keine Bedeutung bei der Stabilit

atsanalyse linearer

Systeme. Diese kann man bekanntlich anhand der Systemeigenwerte einfa-

cher durchf

uhren. Seine Bedeutung liegt vielmehr in der Entwurfstheorie vie-

ler nichtlinearer Regelungen und auch in der Stabilit

atsanalyse linearisierter

nichtlinearer Systeme. Wir werden uns diesen Themen sp

ater noch widmen.

2.4.4 Die direkte Methode f

ur zeitdiskrete Systeme

Ahnlich wie im Fall kontinuierlicher Systeme kann die direkte Methode von

Ljapunov auch bei zeitdiskreten Systemen

k+1

= f(x

)

genutzt werden. Die ersten beiden Bedingungen des Stabilit

atssatzes 9, V (0)=

0 und V (x) > 0f

ur alle x = 0, gelten unvermindert. Lediglich die dritte Be-

dingung,

V (x) < 0f

ur alle x = 0,

die wir hier nur f

ur den asymptotisch stabilen Fall betrachten, ist durch die

Bedingung

ΔV

= V (x

k+1

) − V (x

) < 0f

ur alle x

= 0

zu ersetzen.

Im Fall linearer Systeme

k+1

= Φx

und quadratischer Ljapunov-Funktionen

V (x)=x

erh

alt man

ΔV

= x

k+1

− x

= x

RΦx

− x

= x

(Φ

RΦ− R)x

< 0.

Die obige Ungleichung ist oﬀensichtlich erf

ullt, wenn die Matrix Q in der

Gleichung

RΦ− R = −Q (2.23)

positiv deﬁnit ist. Gl. (2.23) wird als diskrete Ljapunov-Gleichung bezeich-

net. Im Gegensatz zur Ljapunov-Gleichung im kontinuierlichen Fall ist die

Ljapunov-Gleichung (2.23) quadratisch von der Systemmatrix Φ abh

angig.