Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

1.4.2 Brackets

Brackets are used to avoid any misunderstanding about the way an expression is to be evalu-

ated. Suppose that a group of students is asked to ﬁnd the value of

1 − 3 + 5

One suspects that the majority of students would say that the answer is 3, which is found by

ﬁrst subtracting 3 from 1 and then adding 5. However, there is a fair chance that some might

produce −7, thinking that they should ﬁrst add 3 and 5 and then subtract the result from 1.

(There may be other students who obtain different values entirely, but we had better

forget about them!) In a sense both answers are correct since, as it stands, the expression is

ambiguous. To overcome this, brackets are introduced, using the convention that things inside

brackets are evaluated ﬁrst. Hence we would either write

(1 − 3) + 5

to indicate that subtraction is performed ﬁrst, or write

1 − (3 + 5)

to indicate that addition is performed ﬁrst. In fact, brackets have already been used in Section

1.1 in the context of multiplying negative numbers. For example, on page 18 we wrote

(−2) × (−4) × (−1) × 2 × (−1) × (−3)

which is much easier to interpret than its bracketless counterpart

−2 ×−4 ×−1 × 2 ×−1 ×−3

It is also conventional to suppress the multiplication sign when multiplying brackets together,

so the above product could be written as

(−2)(−4)(−1)(2)(−1)(−3)

Similarly, the multiplication sign is implied in

(5 − 2)(7 + 1)

which is the product of 3 and 8.

Linear Equations

Advice

You should check your answer using a couple of test values. Substituting x = 1 (which lies to

the right of −2, so should work) into both sides of the original inequality 2x + 3 < 4x + 7

gives 5 < 11, which is true. On the other hand, substituting x =−3 (which lies to the left

of −2, so should fail) gives −3 < −5, which is false.

Of course, just checking a couple of numbers like this does not prove that the final

inequality is correct, but it should protect you against gross blunders.

Practice Problem

2 Simplify the inequalities

(a)

2x < 3x + 7 (b) 21x − 19 ≥ 4x + 15

MFE_C01d.qxd 16/12/2005 10:57 Page 70

Incidentally, if you really are confronted with the calculation

1 − 3 + 5

you should perform the subtraction ﬁrst. Of course, in BIDMAS (see page 10) the operations

of addition and subtraction have equal precedence. However, it is generally accepted that in

these circumstances you work from left to right, which in this case means working out 1 – 3

ﬁrst, before adding on the 5, to get the answer of 3.

1.4 • Algebra

Practice Problem

3 (1) Without using your calculator evaluate

(a)

(1 − 3) + 10 (b) 1 − (3 + 10) (c) 2(3 + 4)

(d) 8 − 7 + 3 (e) (15 − 8)(2 + 6) (f) ((2 − 3) + 7) ÷ 6

(2) Confirm your answer to part (1) using a calculator.

Example

Evaluate

(a) (12 − 8) − (6 − 5) (b) 12 − (8 − 6) − 5 (c) 12 − 8 − 6 − 5

Solution

(a) (12 − 8) − (6 − 5) = 4 − 1 = 3

(b) 12 − (8 − 6) − 5 = 12 − 2 − 5 = 10 − 5 = 5

The following problem gives you an opportunity to try out these conventions for yourself

and to use the brackets facility on your calculator.

In mathematics it is necessary to handle expressions in which some of the terms involve let-

ters as well as numbers. It is useful to be able to take an expression containing brackets and to

rewrite it as an equivalent expression without brackets and vice versa. The process of removing

brackets is called ‘expanding the brackets’ or ‘multiplying out the brackets’. This is based on the

distributive law, which states that for any three numbers a, b and c

It is easy to verify this law in simple cases. For example, if a = 2, b = 3 and c = 4 then the left-

hand side is

2(3 + 4) = 2 × 7 = 14

a(b + c) = ab + ac

MFE_C01d.qxd 16/12/2005 10:57 Page 71

However,

ab = 2 × 3 = 6 and ac = 2 × 4 = 8

and so the right-hand side is 6 + 8, which is also 14.

This law can be used when there are any number of terms inside the brackets. We have

a(b + c + d) = ab + ac + ad

a(b + c + d + e) = ab + ac + ad + ae

and so on.

It does not matter in which order two numbers are multiplied, so we also have

(b + c)a = ab + ac + ad

(b + c + d)a = ba + ca + da

(b + c + d + e)a = ba + ca + da + ea

Linear Equations

Example

Multiply out the brackets in

(a) x(x − 2)

(b) 2(x + y − z) + 3(z + y)

Solution

(a) The use of the distributive law to multiply out x(x − 2) is straightforward. This gives

x(x − 2) = xx − x2

It is usual in mathematics to abbreviate xx to x

. It is also standard practice to put the numerical

coefﬁcient in front of the variable, so x2 is usually written 2x. Hence

x(x − 2) = x

− 2x

(b) To expand

2(x + y − z) + 3(z + y)

we need to apply the distributive law twice. We have

2(x + y − z) = 2x + 2y − 2z

3(z + y) = 3z + 3y

Adding together gives

2(x + y − z) + 3(z + y) = 2x + 2y − 2z + 3z + 3y

We could stop at this point. Note, however, that some of the terms are similar. Towards the beginning

of the expression there is a term 2y, whereas at the end there is a like term 3y. Obviously these can be

collected together to make a total of 5y. A similar process can be applied to the terms involving z. The

expression simpliﬁes to

2x + 5y + z

MFE_C01d.qxd 16/12/2005 10:57 Page 72

x + 3y − (2y + x)

However, note that

−(2y + x)

is the same as

(−1)(2y + x)

which expands to give

(−1)(2y) + (−1)x =−2y − x

Hence

x + 3y − (2y + x) = x + 3y − 2y − x = y

after collecting like terms.

1.4 • Algebra

Advice

In this example the solutions are written out in painstaking detail. This is done to show

you precisely how the distributive law is applied. The solutions to all three parts could have

been written down in only one or two steps of working. You are, of course, at liberty to

compress the working in your own solutions, but please do not be tempted to overdo this.

You might want to check your answers at a later date and may find it difficult if you have

tried to be too clever.

Practice Problem

4 Multiply out the brackets, simplifying your answer as far as possible.

(a)

(5 − 2z)z (b) 6(x − y) + 3( y − 2x) (c) x − y + z − (x

+ x − y)

We conclude our discussion of brackets by describing how to multiply two brackets

together. This is based on the result

(a + b)(c + d) = ac + ad + bc + bd

At ﬁrst sight this formula might appear to be totally unmemorable. In fact, all you have to do

is to multiply each term in the ﬁrst pair of brackets by each term in the second in all possible

combinations: that is,

MFE_C01d.qxd 16/12/2005 10:57 Page 73

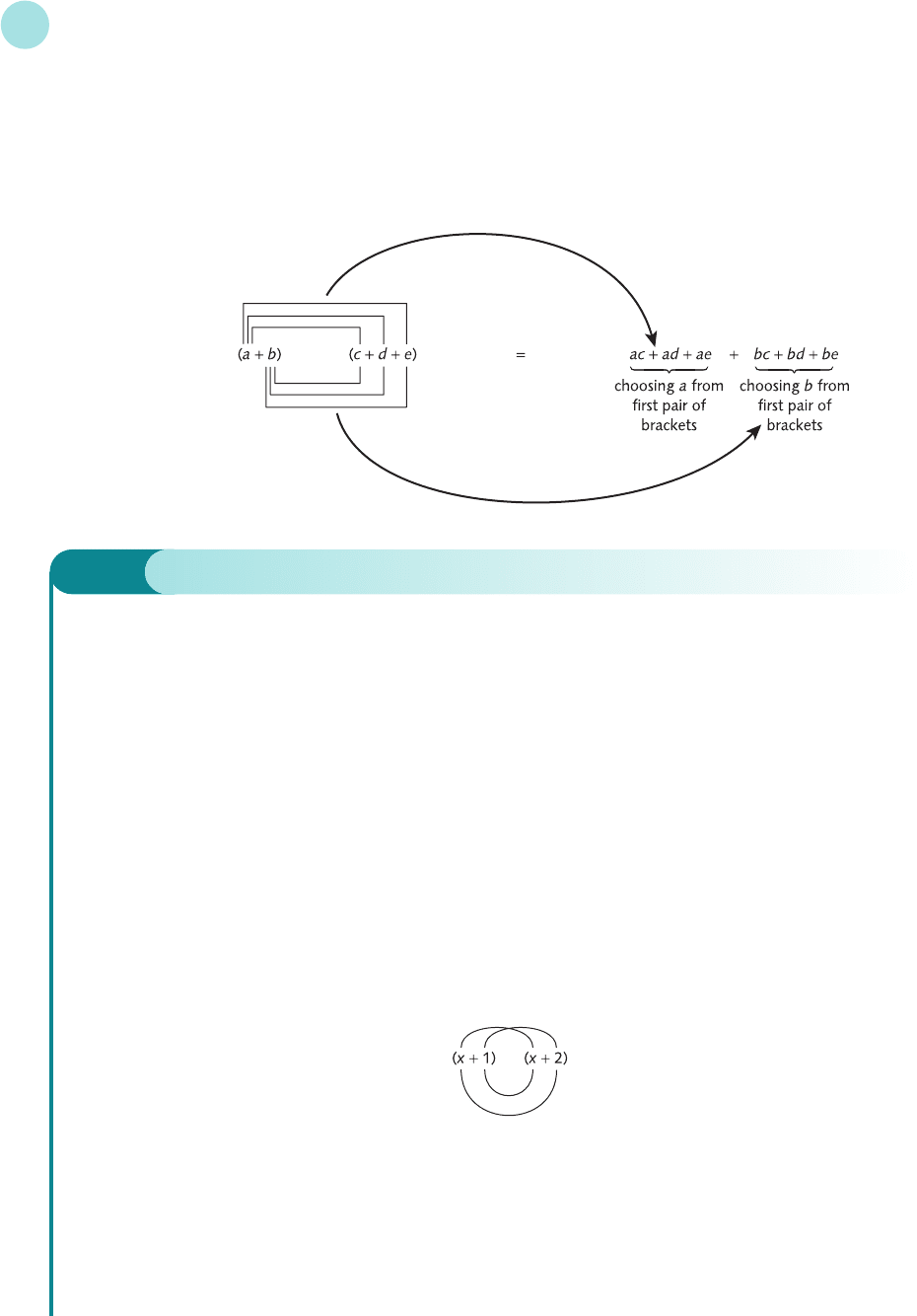
This rule then extends to brackets with more than two terms. For example, to multiply out

(a + b)(c + d + e)

notice that the ﬁrst pair of brackets has two terms and the second has three terms. So, to form

each individual product, we can pick from one of two terms in the ﬁrst pair of brackets and

from one of three terms in the second. There are then six possibilities in total, giving

Linear Equations

Example

Multiply out the brackets

(a) (x + 1)(x + 2) (b) (x + 5)(x − 5) (c) (2x − y)(x + y − 6)

simplifying your answer as far as possible.

Solution

(a) (x + 1)(x + 2) = xx + x2 + 1x + (1)(2)

If we use the abbreviation x

for xx and the convention that numerical coefﬁcients are placed in front

of the variable then this can be written as

+ 2x + x + 2

Finally, collecting like terms gives

+ 3x + 2

If you ﬁnd it difﬁcult to remember how to multiply out brackets, you might like to look at the ‘smiley face’

You get

left eyebrow = x × x = x

right eyebrow = 1 × 2 = 2

nose = 1 × x = x

mouth = x × 2 = 2x

giving a total of x

+ 3x + 2.

MFE_C01d.qxd 16/12/2005 10:57 Page 74

(b)

More formally,

(x + 5)(x − 5) = x

− 5x + 5x − 25

= x

− 25

= 2x

+ 2xy − 12x − yx − y

+ 6y

It might seem that there are no like terms, but since it does not matter in which order two numbers are

multiplied, yx is the same as xy. The terms 2xy and −yx can therefore be combined to give

2xy − xy = xy

Hence the simpliﬁed expression is

+ xy − 12x − y

+ 6y

1.4 • Algebra

Practice Problem

5 Multiply out the brackets.

(a)

(x + 3)(x − 2)

(b) (x + y)(x − y)

(d) (5x + 2y)(x − y + 1)

Looking back at part (b) of the previous worked example, notice that

(x + 5)(x − 5)

can be written as

− 5

Quite generally

(a + b)(a − b) = a

− ab + ba − b

= a

− ab + ab − b

= a

− b

The result

is called the difference of two squares formula. It provides a quick way of factorizing an

expression: that is, of producing an equivalent expression with brackets.

− b

= (a + b)(a − b)

MFE_C01d.qxd 16/12/2005 10:57 Page 75

Linear Equations

Example

Factorize the following expressions:

(a) x

− 16 (b) 9x

− 100

Solution

(a) Noting that

− 16 = x

− 4

we can use the difference of two squares formula to deduce that

− 16 = (x + 4)(x − 4)

(b) Noting that

− 100 = (3x)

− (10)

we can use the difference of two squares formula to deduce that

− 100 = (3x + 10)(3x − 10)

Practice Problem

6 Factorize the following expressions:

(a)

− 64 (b) 4x

− 81

1.4.3 Fractions

For a numerical fraction such as

the number 7, on the top, is called the numerator and the number 8, on the bottom, is called the

denominator. In this book we are also interested in the case when the numerator and denom-

inator involve letters as well as numbers. These are referred to as algebraic fractions. For example,

and

are both algebraic fractions. The letters x, y and z are used to represent numbers, so the rules

for the manipulation of algebraic fractions are the same as those for ordinary numerical frac-

tions. The rules for multiplication and division are as follows.

to multiply fractions you multiply their

corresponding numerators and denominators

− 1

y + z

− 2

MFE_C01d.qxd 16/12/2005 10:57 Page 76

1.4 • Algebra

Example

Calculate

(a) ×

(b) 2 ×

(d) ÷ 3

Solution

(a) The multiplication rule gives

×= =

We could leave the answer like this, although it can be simpliﬁed by dividing top and bottom by 2 to

get

The two answers are equivalent. If a cake is cut into 6 pieces and you eat 5 of them then you eat just

as much as someone who cuts the cake into 12 pieces and eats 10 (although it might appear that you are

not such a glutton). It is also valid to ‘cancel’ by 2 at the very beginning: that is,

×= =

(b) The whole number 2 is equivalent to the fraction

/1, so

2 ×=×= =

2 × 6

1 × 13

1 × 5

3 × 2

2 × 5

3 × 4



In symbols,

×= =

to divide by a fraction you turn it upside down and multiply

In symbols,

÷=×

a × c

b × d

MFE_C01d.qxd 16/12/2005 10:57 Page 77

the divisor is turned upside down to get

4 and then multiplied to get

÷=× = =

(d) We write 3 as

, so

÷ 3 =÷=×=

3 × 3

1 × 2

Linear Equations

Example

Calculate

(a) + (b) + (c) −

Solution

(a) The fractions

/5 and

/5 already have the same denominator, so to add them we just add their numer-

ators to get

+= =

(b) The fractions

and

have denominators 4 and 3. One number that is divisible by both 3 and 4 is 12,

so we choose this as the common denominator. Now 4 goes into 12 exactly 3 times, so

1 × 3

4 × 3

1 + 2

Practice Problem

7 (1) Without using a calculator evaluate

(a)

× (b) 7 × (c) ÷ (d) ÷ 16

(2) Confirm your answer to part (1) using a calculator.

The rules for addition and subtraction are as follows:

to add (or subtract) two fractions you put them over a common

denominator and add (or subtract) their numerators

MFE_C01d.qxd 16/12/2005 10:57 Page 78

and 3 goes into 12 exactly 4 times, so

Hence

+=+= =

/12 and

/8 have denominators 12 and 8. One number that is divisible by both 12 and 8 is

24, so we choose this as the common denominator. Now 12 goes into 24 exactly twice, so

and 8 goes into 24 exactly 3 times, so

Hence

−=−=−

It is not essential that the lowest common denominator is used. Any number will do provided that it is

divisible by the two original denominators. If you are stuck then you could always multiply the original

two denominators together. In part (c) the denominators multiply to give 96, so this can be used

instead. Now

and

−=−= = =−

as before.

−4

56 − 60

5 × 12

7 × 8

5 × 3

7 × 2

3 + 8

2 × 4

3 × 4

1.4 • Algebra

Practice Problem

8 (1) Without using a calculator evaluate

(a)

− (b) + (c) −

(2) Confirm your answer to part (1) using a calculator.

Provided that you can manipulate ordinary fractions, there is no reason why you should not

be able to manipulate algebraic fractions just as easily, since the rules are the same.

MFE_C01d.qxd 16/12/2005 10:57 Page 79