Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

Linear Equations

Example

Find expressions for each of the following:

(a) ×

(b) ÷

(d) −

Solution

(a) To multiply two fractions we multiply their corresponding numerators and denominators, so

×= =

(b) To divide by

we turn it upside down and multiply, so

÷=×=

and

already have the same denominator, so to add them we just add their numerators to get

+= =

(d) The fractions

and

have denominators x + 2 and x + 1. An obvious common denominator is given by their product,

(x + 2)(x + 1). Now x + 2 goes into (x + 2)(x + 1) exactly x + 1 times, so

x(x + 1)

(x + 2)(x + 1)

x + 2

x + 1

x + 2

2x − 5

+ 2

x + 1 + x − 6

+ 2

x − 6

+ 2

x + 1

+ 2

x − 6

+ 2

x + 1

+ 2

x − 1

(x − 1)(x + 4)

(x − 1)x(x + 4)

x(x + 4)

x − 1

x + 1

x + 2

x − 6

+ 2

x + 1

+ 2

x − 1

x(x + 4)

x − 1

MFE_C01d.qxd 16/12/2005 10:57 Page 80

Also x + 1 goes into (x + 2)(x + 1) exactly x + 2 times, so

Hence

−=−=

It is worth multiplying out the brackets on the top to simplify: that is,

− 2

(x + 2)(x + 1)

+ x − x − 2

(x + 2)(x + 1)

x(x + 1) − (x + 2)

(x + 2)(x + 1)

(x + 2)

(x + 2)(x + 1)

x(x + 1)

(x + 2)(x + 1)

x + 1

x + 2

x(x + 1)

(x + 2)(x + 1)

x + 1

1.4 • Algebra

Practice Problem

9 Find expressions for the following algebraic fractions, simplifying your answers as far as possible.

(a)

× (b) ÷ (c) + (d) −

x + 2

x + 1

x + 10

x − 1

x + 2

x − 1

1.4.4 Equations

In the course of working through the ﬁrst section of this chapter, you will have learnt how to

solve simple equations such as

3x + 1 = 13

Such problems are solved by ‘doing the same thing to both sides’. For this particular equation,

the steps would be

3x = 12 (subtract 1 from both sides)

x = 4 (divide both sides by 3)

We now show how to solve more complicated equations. The good news is that the basic

method is the same.

Example

Solve

(a) 6x + 1 = 10x − 9 (b) 3(x − 1) + 2(2x + 1) = 4

x − 6

2x + 1

x + 2

3x − 1

MFE_C01d.qxd 16/12/2005 10:57 Page 81

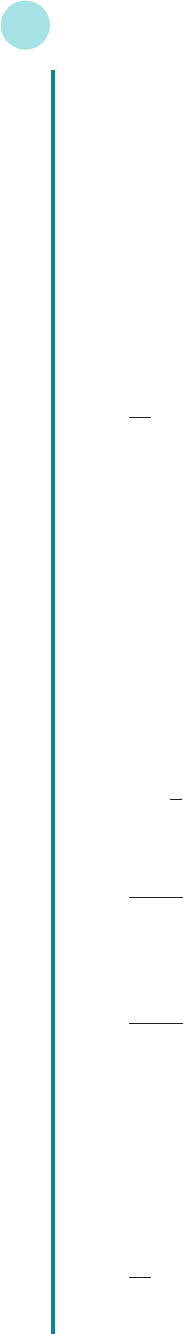
Solution

(a) To solve

6x + 1 = 10x − 9

the strategy is to collect terms involving x on one side of the equation, and to collect all of the number

terms on to the other side. It does not matter which way round this is done. In this particular case,

there are more x’s on the right-hand side than there are on the left-hand side. Consequently, to

avoid negative numbers, you may prefer to stack the x terms on the right-hand side. The details are as

follows:

1 = 4x − 9 (subtract 6x from both sides)

10 = 4x (add 9 to both sides)

= x (divide both sides by 4)

Hence x =

/2 = 2

/2.

(b) The novel feature of the equation

3(x − 1) + 2(2x + 1) = 4

is the presence of brackets. To solve it, we ﬁrst remove the brackets by multiplying out, and then collect

like terms:

3x − 3 + 4x + 2 = 4 (multiply out the brackets)

7x − 1 = 4 (collect like terms)

Note that this equation is now of the form that we know how to solve:

7x = 5 (add 1 to both sides)

x = (divide both sides by 7)

= 7

is the fact that it involves an algebraic fraction. This can easily be removed by multiplying both sides by

the bottom of the fraction:

× (3x − 1) = 7(3x − 1)

which cancels down to give

20 = 7(3x − 1)

The remaining steps are similar to those in part (b):

20 = 21x − 7 (multiply out the brackets)

27 = 21x (add 7 to both sides)

= x (divide both sides by 21)

Hence x =

/7 = 1

/7.

3x − 1

Linear Equations

MFE_C01d.qxd 16/12/2005 10:57 Page 82

(d) The next equation,

looks particularly daunting since there are fractions on both sides. However, these are easily removed

by multiplying both sides by the denominators, in turn:

9 = (multiply both sides by x + 2)

9(2x + 1) = 7(x + 2) (multiply both sides by 2x + 1)

With practice you can do these two steps simultaneously and write this as the ﬁrst line of working. The

procedure of going straight from

9(2x + 1) = 7(x + 2)

is called ‘cross-multiplication’. In general, if

then

ad = bc

The remaining steps are similar to those used in the earlier parts of this example:

18x + 9 = 7x + 14 (multiply out the brackets)

11x + 9 = 14 (subtract 7x from both sides)

11x = 5 (subtract 9 from both sides)

x = (divide both sides by 11)

(e) The left-hand side of the ﬁnal equation

= 2

is surrounded by a square root, which can easily be removed by squaring both sides to get

= 4

The remaining steps are ‘standard’:

2x = 4(x − 6) (multiply both sides by x − 6)

2x = 4x − 24 (multiply out the brackets)

−2x =−24 (subtract 4x from both sides)

x = 12 (divide both sides by −2)

x − 6

2x + 1

x + 2

7(x + 2)

2x + 1

x + 2

1.4 • Algebra

MFE_C01d.qxd 16/12/2005 10:57 Page 83

Looking back over each part of the previous example, notice that there is a common strategy.

In each case, the aim is to convert the given equation into one of the form

ax + b = c

which is the sort of equation that we can easily solve. If the original equation contains brackets

then remove them by multiplying out. If the equation involves fractions then remove them by

cross-multiplying.

Linear Equations

Advice

If you have the time, it is always worth checking your answer by substituting your

solution back into the original equation. For the last part of the above example, putting

x = 12 into gives

==4 = 2 ✓

2 × 12

12 − 6

x − 6

Practice Problem

10 Solve each of the following equations. Leave your answer as a fraction, if necessary.

(a)

4x + 5 = 5x − 7 (b) 3(3 − 2x) + 2(x − 1) = 10

x − 1

Algebraic fraction Ratio of two expressions; p(x)/q(x) where p(x) and q(x) are algebraic

expressions such as ax

+ bx + c or dx + e.

Denominator The number (or expression) on the bottom of a fraction.

Distributive law (for multiplication over addition) The rule which states that

a(b + c) = ab + ac, for any numbers, a, b and c.

Number line An inﬁnite line on which the points represent real numbers by their (signed)

distance from the origin.

Numerator The number (or expression) on the top of a fraction.

Key Terms

Practice Problems

11 Which of the following inequalities are true?

(a)

−2 < 1 (b) −6 > −4 (c) 3 < 3

(d) 3 ≤ 3 (e) −21 ≥−22 (f) 4 < √25

MFE_C01d.qxd 16/12/2005 10:57 Page 84

12 Simplify the following inequalities:

(a) 2x > x + 1

(b) 7x + 3 ≤ 9 + 5x

(d) x − 1 < 2x − 3

13 Without using a calculator work out

(a)

(5 − 2)

(b) 5

− 2

Is it true in general that (a − b)

= a

− b

14 Use your calculator to work out the following. Round your answer, if necessary, to 2 decimal places.

(a)

5.31 × 8.47 − 1.01

(b) (8.34 + 2.27)/9.41

(e) 45.76 − (2.55 + 15.83) (f) (3.45 − 5.38)

(g) 4.56(9.02 + 4.73) (h) 6.85/(2.59 + 0.28)

15 Simplify the following expressions by collecting together like terms:

(a)

2x + 3y + 4x − y (b) 2x

− 5x + 9x

+ 2x − 3

(e) 2(5a + b) − 4b (f) 5(x − 4y) + 6(2x + 7y)

(g) 5 − 3( p − 2) (h) +

16 Multiply out the brackets.

(a)

7(x − y) (b) (5x − 2y)z (c) y + 2z − 2(x + 3y − z)

(d) (x − 5)(x − 2) (e) x(x − y + 7) (f) x(x + 1)(x + 2) (g) (x − 1)(x + 1 − y)

17 (1) Use the formula for the difference of two squares to factorize

(a)

− 4 (b) x

− y

− 100y

(d) a

− 25

(2) Use the formula for the difference of two squares to evaluate the following without using a

calculator:

(a)

50 563

− 49 437

(b) 90

− 89.99

− 541

(d) 123 456 789

− 123 456 788

18 (1) Without using your calculator evaluate

(a)

× (b) ×× (c) ÷ (d) ×÷

(e) − (f) + (g) 2 + 1 (h) 5 −+ 1

(i) 3 × 1 (j) ×+ (k) × 2 − 1 (l) 3 ÷ 2 ÷

(2) Confirm your answer to part (1) using a calculator.

x − 1

2x + 3

1.4 • Algebra



MFE_C01d.qxd 16/12/2005 10:57 Page 85

19 Find expressions for the following fractions:

(a)

× (b) ÷ (c) +

(d) + (e) + (f) +

(g) x − (h) −+

20 Solve the following equations:

(a)

5(2x + 1) = 3(x − 2) (b) 5(x + 2) + 4(2x − 3) = 11

(e) 9 − 5(2x − 1) = 6 (f) = 2

(g) = (h) + 3 = 7

(i) 5 −=2 (j) =

(k) √(2x − 5) = 3 (l) (x + 3)(x − 1) = (x + 4)(x − 3)

(m) (x + 2)

+ (2x − 1)

= 5x(x + 1) (n) =+

(o) = 3 (p) −=

2x − 1

x − 4

2x + 7

2(x − 1)

5(x − 3)

5x + 4

x − 1

2x + 1

x + 1

x(x + 1)

x + 1

x − 2

+ 6x

x − 2

Linear Equations

MFE_C01d.qxd 16/12/2005 10:57 Page 86

section 1.5

Transposition of formulae

Mathematical modelling involves the use of formulae to represent the relationship between

economic variables. In microeconomics we have already seen how useful supply and demand

formulae are. These provide a precise relationship between price and quantity. For example,

the connection between price, P, and quantity, Q, might be modelled by

P =−4Q + 100

Given any value of Q it is trivial to deduce the corresponding value of P by merely replacing the

symbol Q by a number. A value of Q = 2, say, gives

P =−4 × 2 + 100

=−8 + 100

= 92

On the other hand, given P, it is necessary to solve an equation to deduce Q. For example, when

P = 40, the equation is

−4Q + 100 = 40

which can be solved as follows:

−4Q =−60 (subtract 100 from both sides)

Q = 15 (divide both sides by −4)

Objectives

At the end of this section you should be able to:

 Manipulate formulae.

 Draw a ﬂow chart representing a formula.

 Use a reverse ﬂow chart to transpose a formula.

 Change the subject of a formula involving several letters.

MFE_C01e.qxd 16/12/2005 10:57 Page 87

This approach is reasonable when only one or two values of P are given. However, if we are

given many values of P, it is clearly tedious and inefﬁcient for us to solve the equation each time

to ﬁnd Q. The preferred approach is to transpose the formula for P. In other words, we re-

arrange the formula

P = an expression involving Q

into

Q = an expression involving P

Written this way round, the formula enables us to ﬁnd Q by replacing P by a number. For the

speciﬁc formula

−4Q + 100 = P

the steps are

−4Q = P − 100 (subtract 100 from both sides)

Q = (divide both sides by −4)

Notice that

=−

/4P + 25

so the rearranged formula simpliﬁes to

Q =−

/4P + 25

If we now wish to ﬁnd Q when P = 40, we immediately get

Q =−

/4 × 40 + 25

=−10 + 25

= 15

The important thing to notice about the algebra is that the individual steps are identical to

those used previously for solving the equation

−4Q + 100 = 40

i.e. the operations are again

‘subtract 100 from both sides’

followed by

‘divide both sides by −4’

100

−4

P − 100

−4

P − 100

−4

Linear Equations

Example

Make x the subject of the formula

x − 2 = y

MFE_C01e.qxd 16/12/2005 10:57 Page 88

Solution

If you needed to solve an equation such as x − 2 = 4, say, you would ﬁrst add 2 to both sides and then

multiply both sides by 7. Performing the same operations to the general equation

x − 2

gives

x = y + 2 (add 2 to both sides)

x = 7(y + 2) (multiply both sides by 7)

If desired, you can multiply out the brackets to give the alternative version:

x = 7y + 14

1.5 • Transposition of formulae

Practice Problem

1 (a) Solve the equation

/2Q + 13 = 17

State clearly exactly what operation you have performed to both sides at each stage of your

solution.

(b) By performing the same operations as part (a), rearrange the formula

/2Q + 13 = P

into the form

Q = an expression involving P

to part (a).

In general, there are two issues concerning formula transposition. Firstly, we need to decide

what to do to both sides of the given formula and the order in which they should be performed.

Secondly, we need to carry out these steps accurately. The ﬁrst of these is often the more

difﬁcult. However, there is a logical strategy that can be used to help. To illustrate this, consider

the task of making Q the subject of

P =

/3Q + 5

that is, of rearranging this formula into the form

Q = an expression involving P

Imagine starting with a value of Q and using a calculator to work out P from

P =

/3Q + 5

The diagram overleaf shows that two operations are required and indicates the order in which

they must be done. This diagram is called a ﬂow chart.

MFE_C01e.qxd 16/12/2005 10:57 Page 89