Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

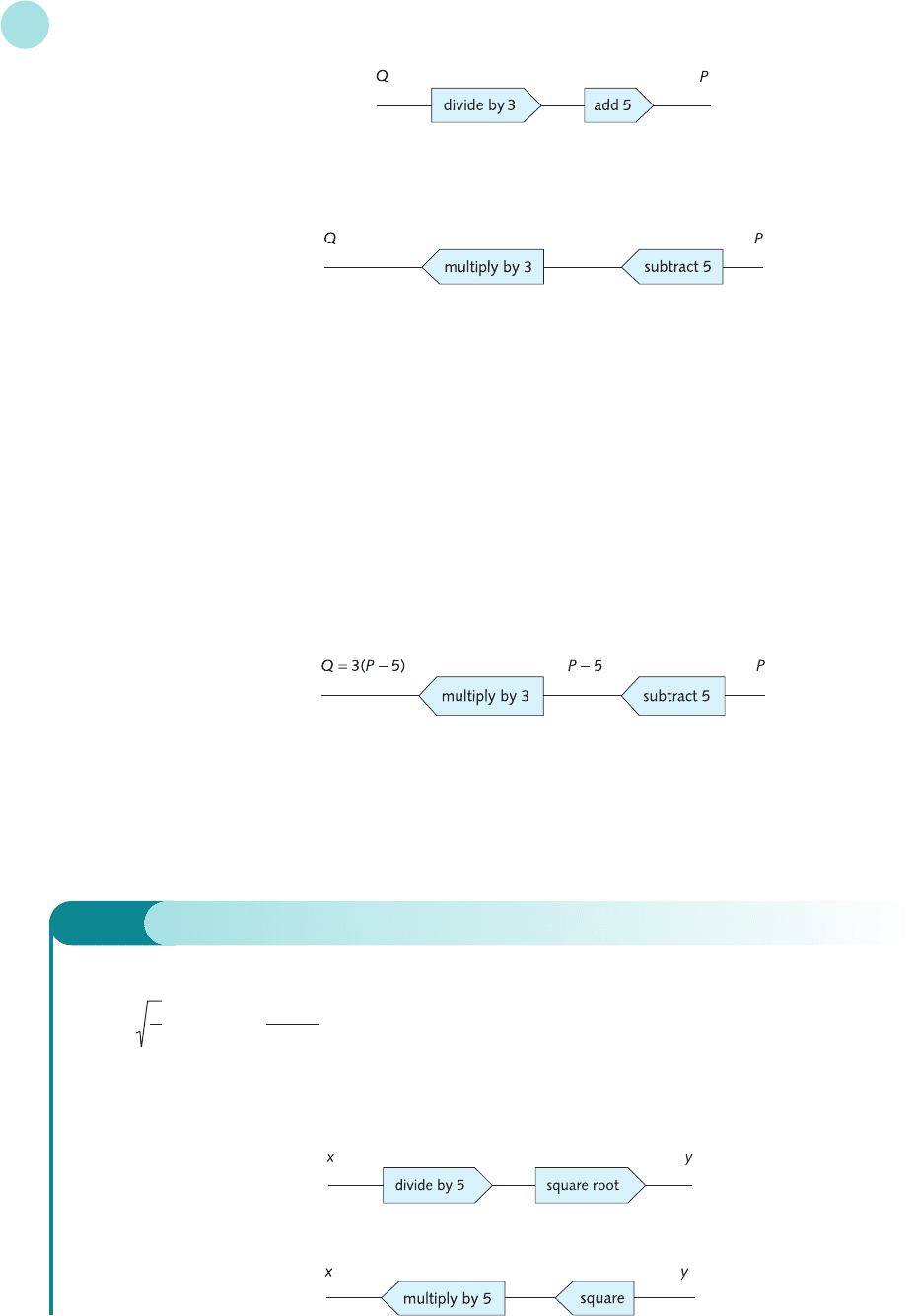
To go backwards from P to Q we need to undo these operations. Now the reverse of ‘divide by

3’ is ‘multiply by 3’ and the reverse of ‘add 5’ is ‘subtract 5’, so the operations needed to trans-

pose the formula are as follows:

This diagram is called a reverse ﬂow chart. The process is similar to that of unwrapping a

parcel (or peeling an onion); you start by unwrapping the outer layer ﬁrst and work inwards.

If we now actually perform these steps in the order speciﬁed by the reverse ﬂow chart, we get

/3Q + 5 = P

/3Q = P − 5 (subtract 5 from both sides)

Q = 3(P − 5) (multiply both sides by 3)

The rearranged formula can be simpliﬁed by multiplying out the brackets to give

Q = 3P − 15

Incidentally, if you prefer, you can actually use the reverse ﬂow chart itself to perform the alge-

bra for you. All you have to do is to pass the letter P through the reverse ﬂow chart. Working

from right to left gives

Notice that by taking P as the input to the box ‘subtract 5’ gives the output P − 5, and if the

whole of this is taken as the input to the box ‘multiply by 3’, the ﬁnal output is the answer,

3(P − 5). Hence

Q = 3(P − 5)

Linear Equations

Example

Make x the subject of

(a) y = (b) y =

Solution

(a) To go from x to y the operations are

so the steps needed to transpose the formula are

2x + 1

MFE_C01e.qxd 16/12/2005 10:57 Page 90

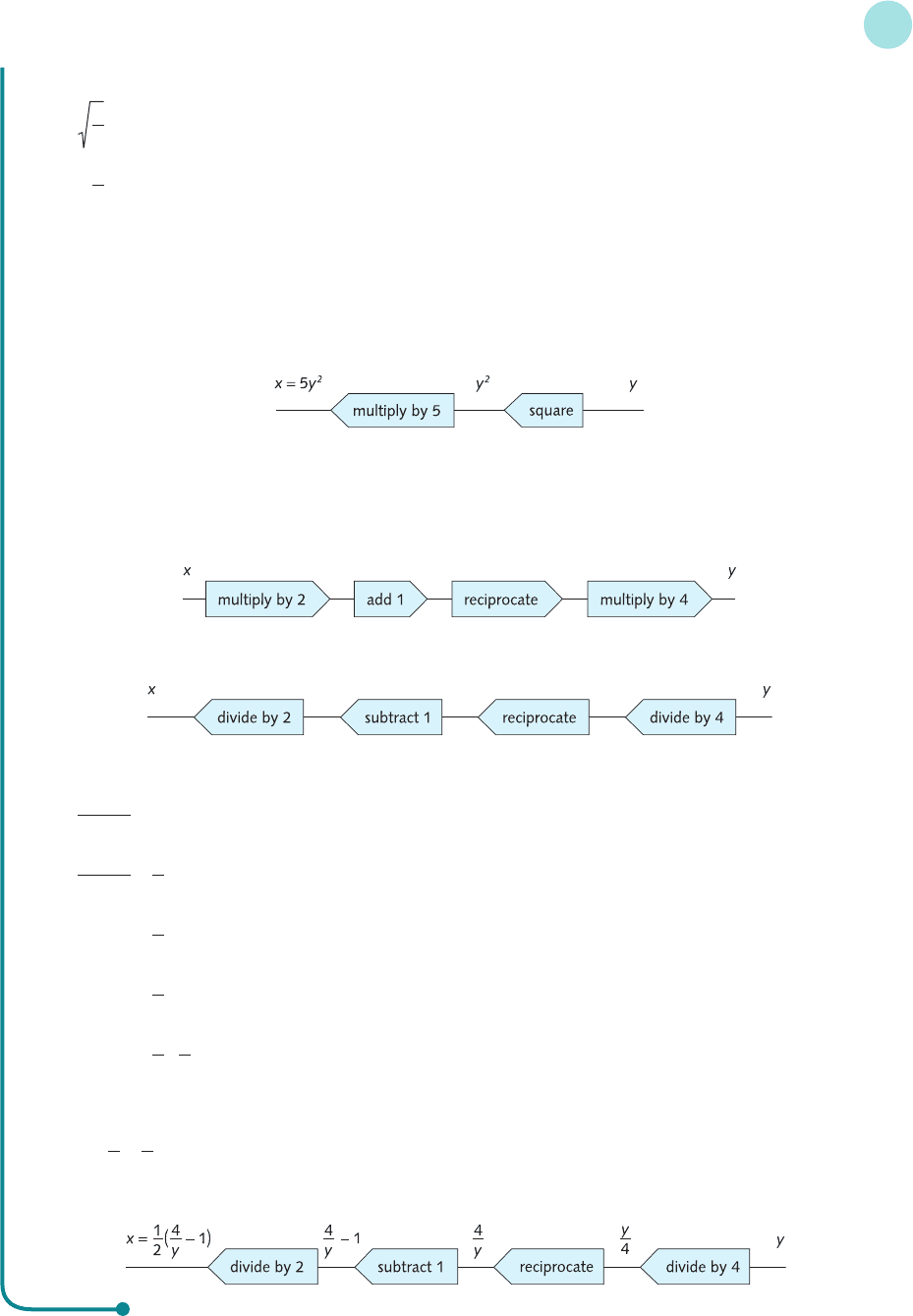
The algebraic details are as follows:

= y

(square both sides)

x = 5y

(multiply both sides by 5)

Hence the transposed formula is

x = 5y

Alternatively, if you prefer, the reverse ﬂow chart can be used directly to obtain

Hence

x = 5y

(b) The forwards ﬂow chart is

so the reverse ﬂow chart is

The algebraic details are as follows:

= y

= (divide both sides by 4)

2x + 1 = (reciprocate both sides)

2x =−1 (subtract 1 from both sides)

x =−1 (divide both sides by 2)

which can be simpliﬁed, by multiplying out the brackets, to give

x =−

Again, the reverse ﬂow chart can be used directly to obtain

2x + 1

1.5 • Transposition of formulae

MFE_C01e.qxd 16/12/2005 10:57 Page 91

The following example contains two difﬁcult instances of transposition. In both cases the

letter x appears more than once on the right-hand side. If this happens, the technique based on

ﬂow charts cannot be used. However, it may still be possible to perform the manipulation even

if some of the steps may not be immediately obvious.

Linear Equations

Example

Transpose the following equations to express x in terms of y :

(a) ax = bx + cy + d (b) y =

Solution

(a) In the equation

ax = bx + cy + d

there are terms involving x on both sides and since we are hoping to rearrange this into the form

x = an expression involving y

it makes sense to collect the x’s on the left-hand side. To do this we subtract bx from both sides to get

ax − bx = cy + d

Notice that x is a common factor of the left-hand side, so the distributive law can be applied ‘in reverse’

to take the x outside the brackets: that is,

(a − b)x = cy + d

Finally, both sides are divided by a − b to get

x =

which is of the desired form.

(b) It is difﬁcult to see where to begin with the equation

y =

because there is an x in both the numerator and the denominator. Indeed, the thing that is preventing

us getting started is precisely the fact that the expression is a fraction. We can, however, remove the frac-

tion simply by multiplying both sides by the denominator to get

(x − 2)y = x + 1

x + 1

x − 2

cy + d

a − b

x + 1

x − 2

Practice Problem

2 Use flow charts to make x the subject of the following formulae:

(a)

y = 6x

(b) y =

7x − 1

MFE_C01e.qxd 16/12/2005 10:57 Page 92

and if we multiply out the brackets then

xy − 2y = x + 1

We want to rearrange this into the form

x = an expression involving y

so we collect the x’s on the left-hand side and put everything else on to the right-hand side. To do this

we ﬁrst add 2y to both sides to get

xy = x + 1 + 2y

and then subtract x from both sides to get

xy − x = 1 + 2y

The distributive law can now be applied ‘in reverse’ to take out the common factor of x: that is,

( y − 1)x = 1 + 2y

Finally, dividing through by y − 1 gives

x =

1 + 2y

y − 1

1.5 • Transposition of formulae

Advice

This example contains some of the hardest

algebraic manipulation seen so far in this

book. I hope that you managed to follow the

individual steps. However, it all might appear

as if we have ‘pulled rabbits out of hats’.

You may feel that, if left on your own, you

are never going to be able to decide what

to do at each stage. Unfortunately there is

no watertight strategy that always works,

although the following five-point plan is worth

considering if you get stuck.

To transpose a given equation of the form

y = an expression involving x

into an equation of the form

x = an expression involving y

you proceed as follows:

Step 1 Remove fractions.

Step 2 Multiply out the brackets.

Step 3 Collect all of the x’s on to the left-hand side.

Step 4 Take out a factor of x.

Step 5 Divide by the coefficient of x.

MFE_C01e.qxd 16/12/2005 10:57 Page 93

Linear Equations

Example

Make x the subject of

y =

Solution

In this formula there is a square root symbol surrounding the right-hand side. This can be removed by

squaring both sides to get

We now apply the ﬁve-step strategy:

Step 1 (cx + d )y

= ax + b

Step 2 cxy

+ dy

= ax + b

Step 3 cxy

− ax = b − dy

Step 4 (cy

− a)x = b − dy

Step 5 x =

b − dy

− a

ax + b

cx + d

ax + b

cx + d

Practice Problem

3 Transpose the following formulae to express x in terms of y:

(a)

x − ay = cx + y

(b) y =

x − 2

x + 4

Flow chart A diagram consisting of boxes of instructions indicating a sequence of

operations and their order.

Reverse ﬂow chart A ﬂow chart indicating the inverse of the original sequence of

operations in reverse order.

Transpose a formula The rearrangement of a formula to make one of the other letters the

subject.

Key Terms

You might find it helpful to look back at the previous example in the light of this strategy.

In part (b) it is easy to identify each of the five steps. Part (a) also used this strategy,

starting with the third step.

MFE_C01e.qxd 16/12/2005 10:57 Page 94

1.5 • Transposition of formulae

Practice Problems

4 Make Q the subject of

P = 2Q + 8

Hence find the value of Q when P = 52.

5 Write down the formula representing each of the following flow charts

(a)

(b)

(c)

(d)

6 Draw flow charts for each of the following formulae:

(a)

y = 5x + 3 (b) y = 5(x + 3) (c) y = 4x

− 6 (d) y =

7 Make x the subject of each of the following formulae:

(a)

y = 9x − 6 (b) y = (x + 4)/3 (c) y =

(d) y =+8 (e) y = (f) y =

8 Transpose the formulae:

(a) Q = aP + b to express P in terms of Q

(b) Y = aY + b + I to express Y in terms of I

(d) V = to express t in terms of V

9 Make x the subject of the following formulae:

(a)

+ b = (b) a − x = (c) e + x + f = g

(d) a = (e) = (f) =

x + a

x − b

x − m

x − n

b + x

5t + 1

t − 1

aP + b

3x − 7

x + 2

+ 8

MFE_C01e.qxd 16/12/2005 10:57 Page 95

section 1.6

National income

determination

Macroeconomics is concerned with the analysis of economic theory and policy at a national

level. In this section we focus on one particular aspect known as national income deter-

mination. We describe how to set up simple models of the national economy which enable

equilibrium levels of income to be calculated. Initially we assume that the economy is divided

into two sectors, households and ﬁrms. Firms use resources such as land, capital, labour and raw

materials to produce goods and services. These resources are known as factors of production

and are taken to belong to households. National income represents the ﬂow of income from

ﬁrms to households given as payment for these factors. Households can then spend this money

in one of two ways. Income can be used for the consumption of goods produced by ﬁrms or

it can be put into savings. Consumption, C, and savings, S, are therefore functions of income,

Y: that is,

C = f(Y)

S = g(Y)

Objectives

At the end of this section you should be able to:

 Identify and sketch linear consumption functions.

 Identify and sketch linear savings functions.

 Set up simple macroeconomic models.

 Calculate equilibrium national income.

 Analyse IS and LM schedules.

MFE_C01f.qxd 16/12/2005 10:58 Page 96

1.6 • National income determination

for some appropriate consumption function, f, and savings function, g. Moreover, C and S are

normally expected to increase as income rises, so f and g are both increasing functions.

We begin by analysing the consumption function. As usual we need to quantify the precise

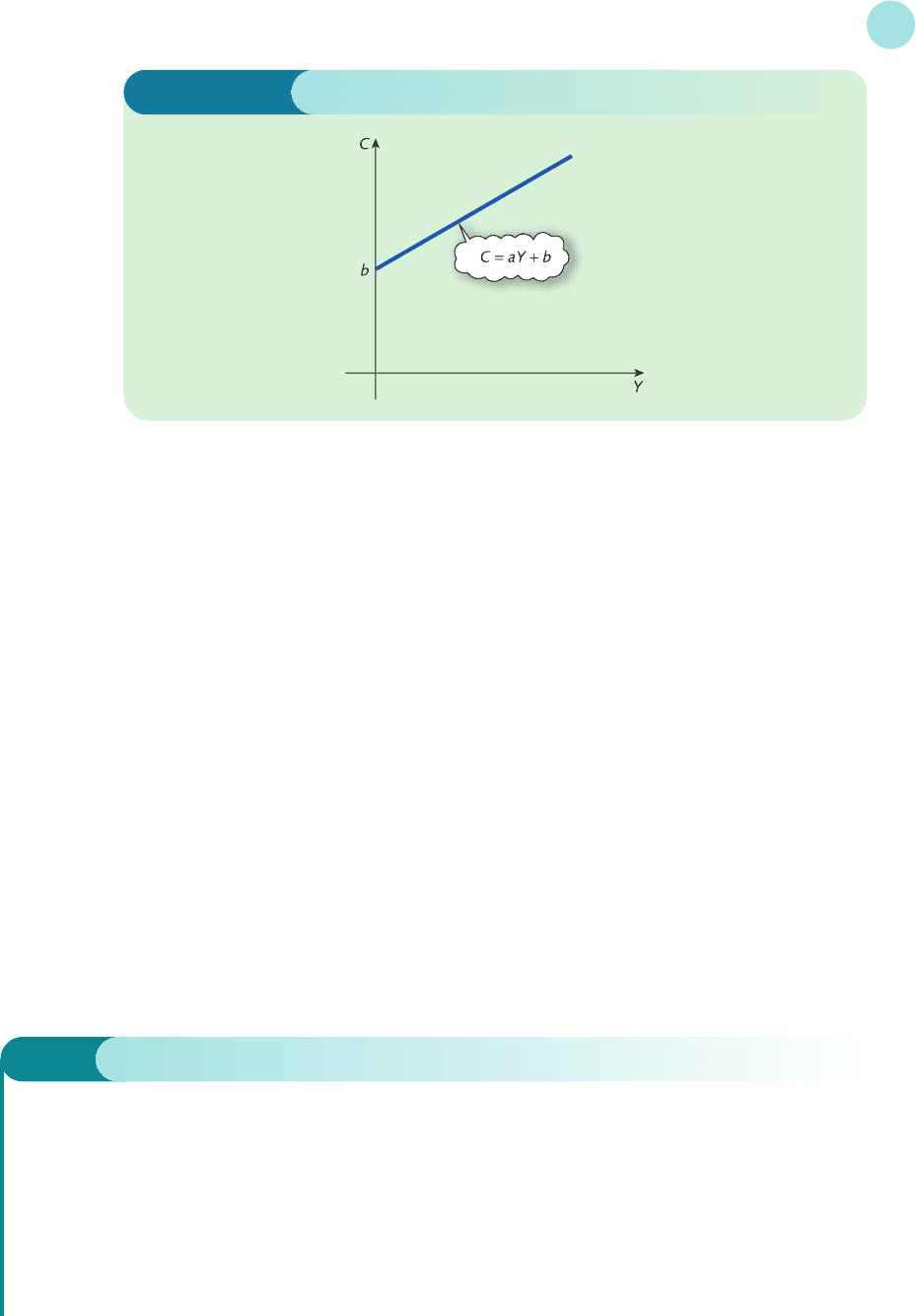
relationship between C and Y. If this relationship is linear then a graph of a typical consump-

tion function is shown in Figure 1.23. It is clear from this graph that if

C = aY + b

then a > 0 and b > 0. The intercept b is the level of consumption when there is no income (that

is, when Y = 0) and is known as autonomous consumption. The slope, a, is the change in C

brought about by a 1 unit increase in Y and is known as the marginal propensity to consume

(MPC). As previously noted, income is used up in consumption and savings so that

Y = C + S

It follows that only a proportion of the 1 unit increase in income is consumed; the rest goes into

savings. Hence the slope, a, is generally smaller than 1: that is, a < 1. It is standard practice in

mathematics to collapse the two separate inequalities a > 0 and a < 1 into the single inequality

0 < a < 1

The relation

Y = C + S

enables the precise form of the savings function to be determined from any given consumption

function. This is illustrated in the following example.

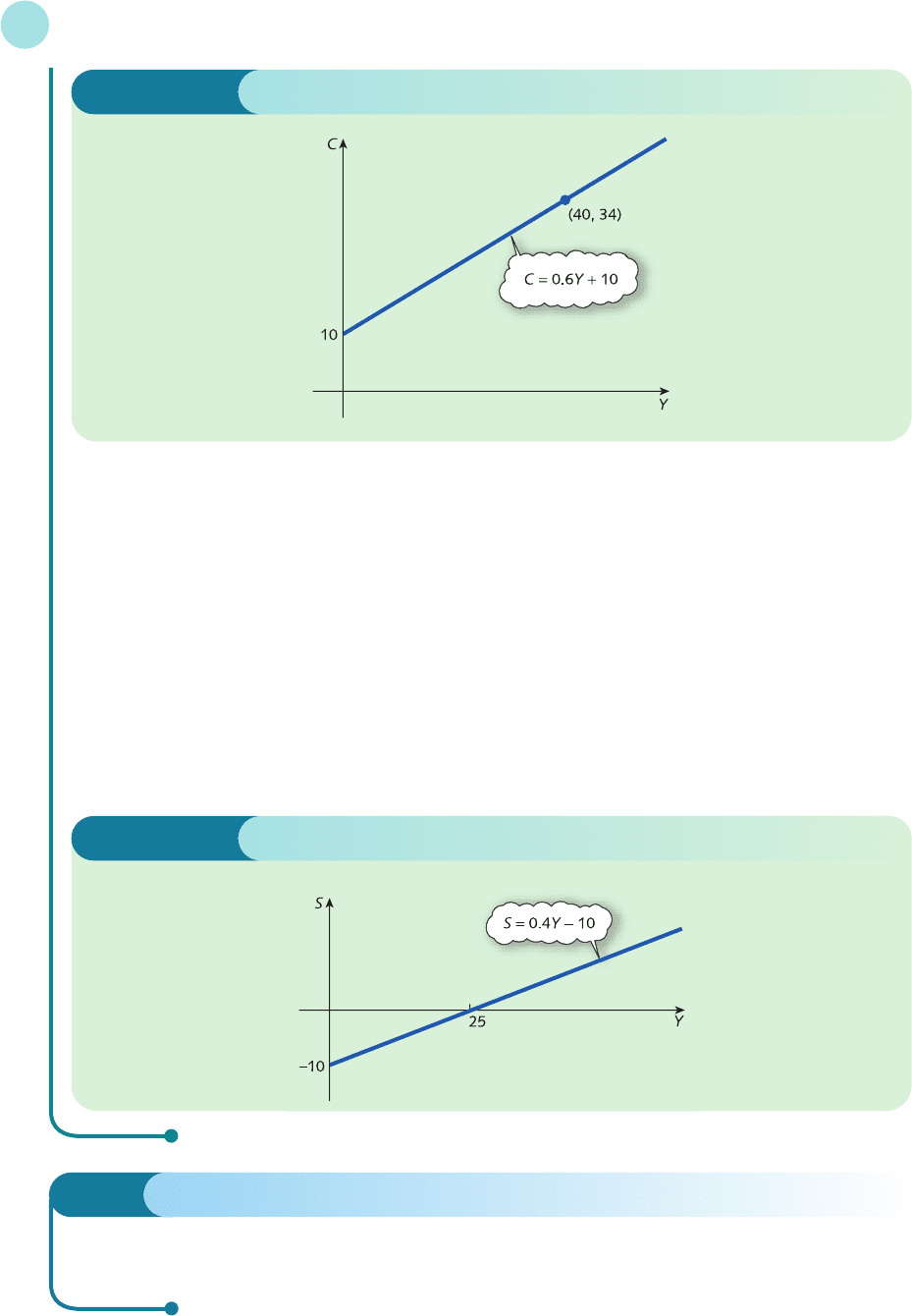
Figure 1.23

Example

Sketch a graph of the consumption function

C = 0.6Y + 10

Determine the corresponding savings function and sketch its graph.

Solution

The graph of the consumption function

C = 0.6Y + 10



MFE_C01f.qxd 16/12/2005 10:58 Page 97

Linear Equations

has intercept 10 and slope 0.6. It passes through (0, 10). For a second point, let us choose Y = 40, which gives

C = 34. Hence the line also passes through (40, 34). The consumption function is sketched in Figure 1.24.

To ﬁnd the savings function we use the relation

Y = C + S

which gives

S = Y − C (subtract C from both sides)

= Y − (0.6Y + 10) (substitute C)

= Y − 0.6Y − 10 (multiply out the brackets)

= 0.4Y − 10 (collect terms)

The savings function is also linear. Its graph has intercept −10 and slope 0.4. This is sketched in Figure 1.25

using the fact that it passes through (0, −10) and (25, 0).

Figure 1.24

Figure 1.25

Practice Problem

1 Determine the savings function that corresponds to the consumption function

C = 0.8Y + 25

MFE_C01f.qxd 16/12/2005 10:58 Page 98

1.6 • National income determination

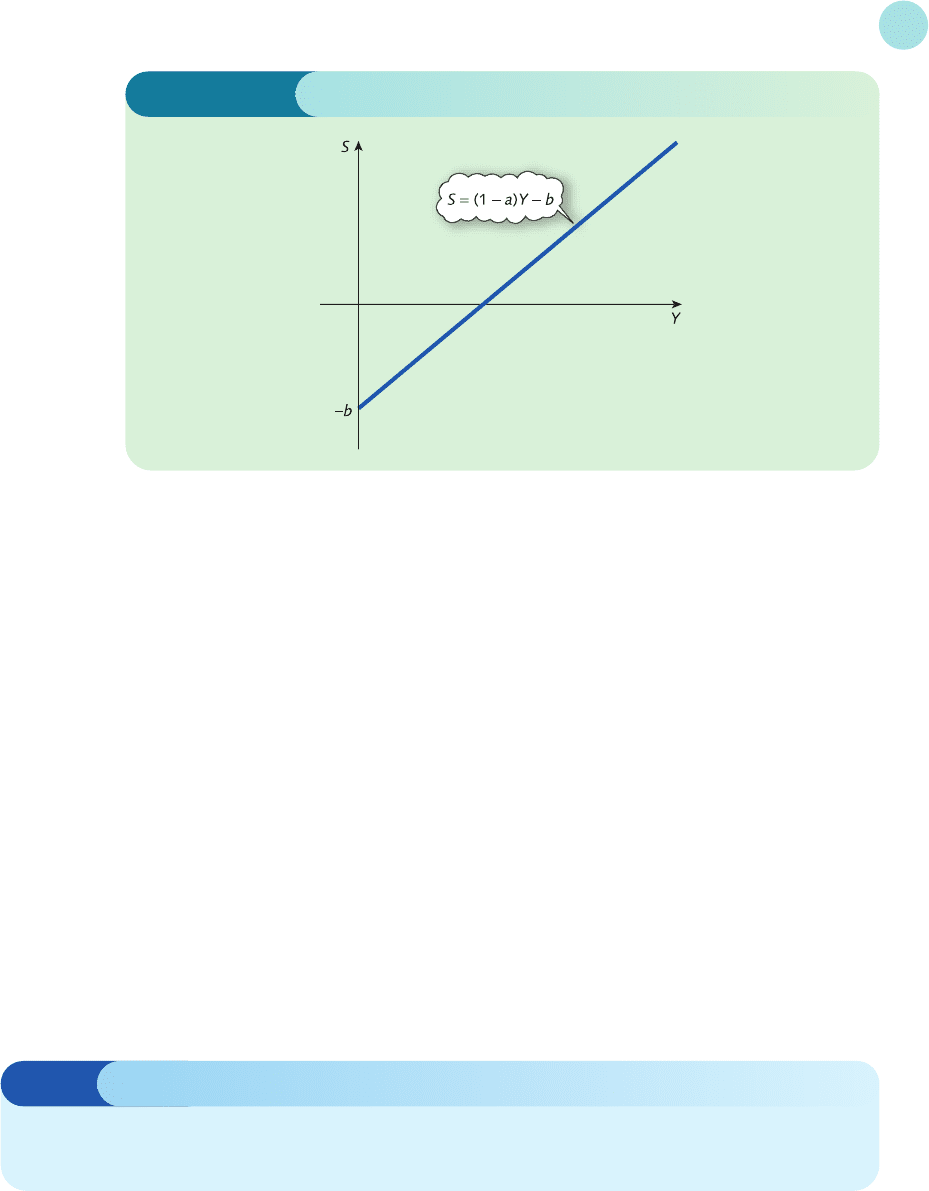
For the general consumption function

C = aY + b

we have

S = Y − C

= Y − (aY + b) (substitute C)

= Y − aY − b (multiply out the brackets)

= (1 − a)Y − b (take out a common factor of Y)

The slope of the savings function is called the marginal propensity to save (MPS) and is given

by 1 − a: that is,

MPS = 1 − a = 1 − MPC

Moreover, since a < 1 we see that the slope, 1 − a, is positive. Figure 1.26 shows the graph of

this savings function. One interesting feature, which contrasts with other economic functions

considered so far, is that it is allowed to take negative values. In particular, note that

autonomous savings (that is, the value of S when Y = 0) are equal to −b, which is negative

because b > 0. This is to be expected because whenever consumption exceeds income, house-

holds must ﬁnance the excess expenditure by withdrawing savings.

Figure 1.26

Advice

The result, MPC + MPS = 1, is always true, even if the consumption function is non-linear.

A proof of this generalization can be found on page 274.

The simplest model of the national economy is illustrated in Figure 1.27, which shows the

circular ﬂow of income and expenditure. This is fairly crude, since it fails to take into account

government activity or foreign trade. In this diagram investment, I, is an injection into the cir-

cular ﬂow in the form of spending on capital goods.

MFE_C01f.qxd 16/12/2005 10:58 Page 99