Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

Linear Equations

110

Figure 1.31

Autonomous consumption The level of consumption when there is no income.

Autonomous savings The withdrawals from savings when there is no income.

Consumption The ﬂow of money from households to ﬁrms as payment for goods and

services.

Consumption function The relationship between national income and consumption.

Disposable income Household income after the deduction of taxes and the addition of

beneﬁts.

Factors of production The inputs to the production of goods and services: land, capital,

labour and raw materials.

Government expenditure The total amount of money spent by government on defence,

education, health, police, etc.

Investment The creation of output not for immediate consumption.

IS schedule The equation relating national income and interest rate based on the assump-

tion of equilibrium in the goods market.

LM schedule The equation relating national income and interest rate based on the

assumption of equilibrium in the money market.

Marginal propensity to consume The fraction of a rise in national income which goes on

consumption. It is the slope of the consumption function.

Marginal propensity to save The fraction of a rise in national income which goes into

savings. It is the slope of the savings function.

Money supply The notes and coins in circulation together with money held in bank deposits.

National income The ﬂow of money from ﬁrms to households.

Key Terms

MFE_C01f.qxd 16/12/2005 10:58 Page 110

1.6 • National income determination

111

Practice Problems

5 If the consumption function is given by

C = 0.7Y + 40

state the values of

(a) autonomous consumption

(b) marginal propensity to consume

Transpose this formula to express Y in terms of C and hence find the value of Y when C = 110.

6 Write down expressions for the savings function given that the consumption function is

(a)

C = 0.9Y + 72 (b) C =

7 For a closed economy with no government intervention the consumption function is

C = 0.6Y + 30

and planned investment is

I = 100

Calculate the equilibrium level of

(a) national income

(b) consumption

8 If

C = aY + b

Y = C + I

I = I*

show that

Y =

and obtain a similar expression for C in terms of a, b and I*.

9 An open economy is in equilibrium when

Y = C + I + G + X − M

b + I*

1 − a

+ 500

Y + 10



Precautionary demand for money Money held in reserve by individuals or ﬁrms to fund

unforeseen future expenditure.

Speculative demand for money Money held back by ﬁrms or individuals for the purpose

of investing in alternative assets, such as government bonds, at some future date.

Taxation Money paid to government based on an individual’s income and wealth (direct

taxation) together with money paid by suppliers of goods or services based on expenditure

(indirect taxation).

Transactions demand for money Money used for everyday transactions of goods and

services.

MFE_C01f.qxd 16/12/2005 10:58 Page 111

Linear Equations

112

where

Y = national income

C = consumption

I = investment

G = government expenditure

X = exports

M = imports

Determine the equilibrium level of income given that

C = 0.8Y + 80

I = 70

G = 130

X = 100

M = 0.2Y + 50

10 Given that

consumption, C = 0.8Y + 60

investment, I =−30r + 740

money supply, M

= 4000

transaction–precautionary demand for money, M

= 0.15Y

speculative demand for money, L

=−20r + 3825

determine the values of national income, Y, and interest rate, r, on the assumption that both the com-

modity and the money markets are in equilibrium.

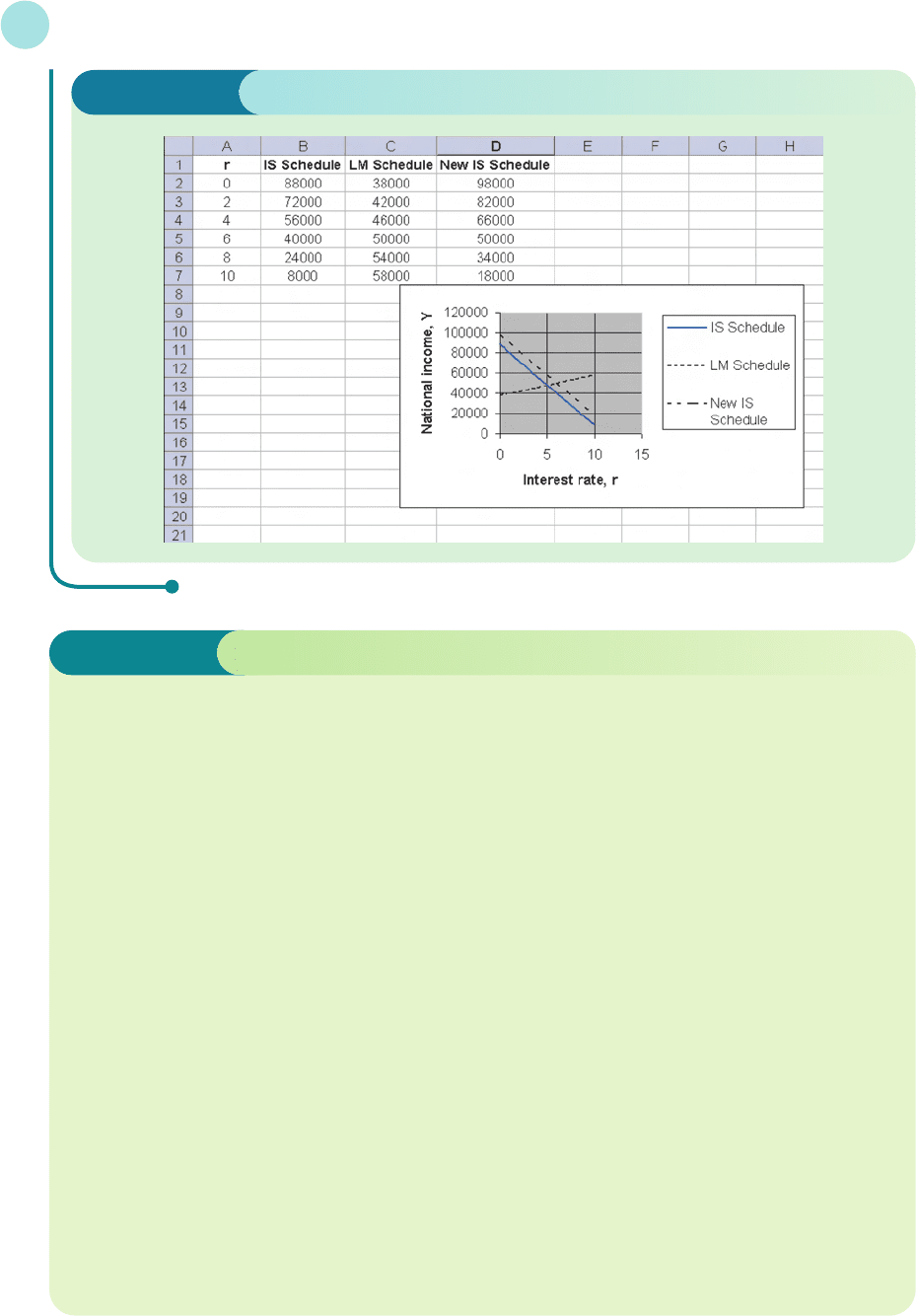
11 (Excel) Consider the consumption function

C = 120 + 0.8Y

where Y

is disposable income.

Write down expressions for C, in terms of national income, Y, when there is

(a) no tax

(b) a lump sum tax of $100

Sketch all three functions on the same diagram, over the range 0 ≤ Y ≤ 800, and briefly describe any

differences or similarities between them.

Sketch the 45 degree line, C = Y, on the same diagram, and hence estimate equilibrium levels of

national income in each case.

12 (Excel) If the consumption function is

C = 0.9Y + 20

and planned investment I = 10, write down an expression for the aggregate expenditure, C + I, in

terms of Y.

Draw graphs of aggregate expenditure, and the 45 degree line, on the same diagram, over the

range 0 ≤ Y ≤ 500. Deduce the equilibrium level of national income.

Describe what happens to the aggregate expenditure line in the case when

(a) the marginal propensity to consume falls to 0.8

(b) planned investment rises to 15

and find the new equilibrium income in each case.

MFE_C01f.qxd 16/12/2005 10:58 Page 112

chapter 2

Non-linear Equations

The main aim of this chapter is to describe the mathematics of non-linear equations.

The approach is similar to that of Chapter 1. There are four sections. Section 2.1

should be read before Section 2.2, and Section 2.3 should be read before

Section 2.4.

The first section investigates the simplest non-linear equation, known as a quadratic.

A quadratic equation can easily be solved either by factorizing it as the product of

two linear factors or by using a special formula. You are also shown how to sketch

the graphs of quadratic functions. The techniques are illustrated by finding the

equilibrium price and quantity for quadratic supply and demand functions.

Section 2.2 introduces additional functions in microeconomics, including revenue

and profit. There is very little new material in this section. It mainly consists of

applying the ideas of Section 2.1 to sketch graphs of quadratic revenue and profit

functions and to find their maximum values.

Finally, the topic of algebra, which we started in Chapter 1, is completed by investi-

gating the rules of indices and logarithms. The basic concepts are covered in Section

2.3. The notation and rules of indices are extremely important and are used fre-

quently in subsequent chapters. Section 2.4 focuses on two specific functions,

namely the exponential and natural logarithm functions. If you run into difficulty, or

are short of time, then this section could be omitted, particularly if you do not intend

to study the next chapter on the mathematics of finance.

MFE_C02a.qxd 16/12/2005 10:59 Page 113

MFE_C02a.qxd 16/12/2005 10:59 Page 114

section 2.1

Quadratic functions

The ﬁrst chapter considered the topic of linear mathematics. In particular, we described how

to sketch the graph of a linear function and how to solve a linear equation (or system of simul-

taneous linear equations). It was also pointed out that not all economic functions are of this

simple form. In assuming that the demand and supply graphs are straight lines, we are certainly

making the mathematical analysis easy, but we may well be sacriﬁcing realism. It may be that

the demand and supply graphs are curved and, in these circumstances, it is essential to model

them using more complicated functions. The simplest non-linear function is known as a

quadratic and takes the form

f(x) = ax

+ bx + c

for some parameters a, b and c. (In fact, even if the demand function is linear, functions derived

from it, such as total revenue and proﬁt, turn out to be quadratic. We investigate these func-

tions in the next section.) For the moment we concentrate on the mathematics of quadratics

and show how to sketch graphs of quadratic functions and how to solve quadratic equations.

Consider the elementary equation

− 9 = 0

Objectives

At the end of this section you should be able to:

 Solve a quadratic equation using ‘the formula’.

 Solve a quadratic equation given its factorization.

 Sketch the graph of a quadratic function using a table of function values.

 Sketch the graph of a quadratic function by ﬁnding the coordinates of the

intercepts.

 Determine equilibrium price and quantity given a pair of quadratic demand and

supply functions.

MFE_C02a.qxd 16/12/2005 10:59 Page 115

It is easy to see that the expression on the left-hand side is a special case of the above with

a = 1, b = 0 and c =−9. To solve this equation we add 9 to both sides to get

= 9

so we need to ﬁnd a number, x, which when multiplied by itself produces the value 9. A

moment’s thought should convince you that there are exactly two numbers that work, namely

3 and −3 because

3 × 3 = 9 and (−3) × (−3) = 9

These two solutions are called the square roots of 9. The symbol √ is reserved for the positive

square root, so in this notation the solutions are √9 and −√9. These are usually combined and

written ±√9. The equation

− 9 = 0

is trivial to solve because the number 9 has obvious square roots. In general, it is necessary to

use a calculator to evaluate square roots. For example, the equation

− 2 = 0

can be written as

= 2

and so has solutions x =±√2. My calculator gives 1.414 213 56 (correct to 8 decimal places) for

the square root of 2, so the above equation has solutions

1.414 213 56 and −1.414 213 56

Non-linear Equations

116

Example

Solve the following quadratic equations:

(a) 5x

− 80 = 0 (b) x

+ 64 = 0 (c) (x + 4)

= 81

Solution

(a) 5x

− 80 = 0

= 80 (add 80 to both sides)

= 16 (divide both sides by 5)

x =±4 (square root both sides)

(b) x

+ 64 = 0

=−64 (subtract 64 from both sides)

This equation does not have a solution because you cannot square a real number and get a negative

answer.

= 81

x + 4 =±9 (square root both sides)

MFE_C02a.qxd 16/12/2005 10:59 Page 116

The two solutions are obtained by taking the + and − signs separately. Taking the + sign,

x + 4 = 9sox = 9 − 4 = 5

Taking the − sign,

x + 4 =−9sox =−9 − 4 =−13

The two solutions are 5 and −13.

2.1 • Quadratic functions

117

Example

Solve the quadratic equations

(a) 2x

+ 9x + 5 = 0

(b) x

− 4x + 4 = 0

− 5x + 6 = 0

Solution

(a) For the equation

+ 9x + 5 = 0

we have a = 2, b = 9 and c = 5. Substituting these values into the formula

x =

−± −bbac

( )

Problem

1 Solve the following quadratic equations. (Round your solutions to 2 decimal places if necessary.)

(a)

− 100 = 0 (b) 2x

− 8 = 0 (c) x

− 3 = 0 (d) x

− 5.72 = 0

(e) x

+ 1 = 0 (f) 3x

+ 6.21 = 0 (g) x

= 0

All of the equations considered in Problem 1 are of the special form

+ c = 0

in which the coefﬁcient of x is zero. To solve more general quadratic equations we use a for-

mula that enables the solutions to be calculated in a few lines of working. It can be shown that

+ bx + c = 0

has solutions

x =

The following example describes how to use this formula. It also illustrates the fact (which

you have already discovered in Practice Problem 1) that a quadratic equation can have two

solutions, one solution or no solutions.

−± −bbac

( )



MFE_C02a.qxd 16/12/2005 10:59 Page 117

gives

x =

The two solutions are obtained by taking the + and − signs separately: that is,

=−0.649 (correct to 3 decimal places)

=−3.851 (correct to 3 decimal places)

It is easy to check that these are solutions by substituting them into the original equation. For example,

putting x =−0.649 into

+ 9x + 5

gives

2(−0.649)

+ 9(−0.649) + 5 = 0.001 402

which is close to zero, as required. We cannot expect to produce an exact value of zero because we

rounded √41 to 3 decimal places. You might like to check for yourself that −3.851 is also a solution.

(b) For the equation

− 4x + 4 = 0

we have a = 1, b =−4 and c = 4. Substituting these values into the formula

x =

gives

x =

Clearly we get the same answer irrespective of whether we take the + or the − sign here. In other words,

this equation has only one solution, x = 2. As a check, substitution of x = 2 into the original equation

gives

(2)

− 4(2) + 4 = 0

− 5x + 6 = 0

41616

( )±−

−− ± − −( ) (( ) ( )( ))

()

44414

−± −bbac

( )

−−941

−+941

−±941

−± −98140

( )

−± −99425

( ()())

()

Non-linear Equations

118

MFE_C02a.qxd 16/12/2005 10:59 Page 118

we have a = 3, b =−5 and c = 6. Substituting these values into the formula

x =

gives

x =

The number under the square root sign is negative and, as you discovered in Practice Problem 1, it is

impossible to ﬁnd the square root of a negative number. We conclude that the quadratic equation

− 5x + 6 = 0

has no solutions.

547

()±−

52572

( )±−

−− ± − −( ) (( ) ( )( ))

()

55436

−± −bbac

( )

2.1 • Quadratic functions

119

This example demonstrates the three cases that can occur when solving quadratic equations.

The precise number of solutions that an equation can have depends on whether the number under

the square root sign is positive, zero or negative. The number b

− 4ac is called the discriminant

because the sign of this number discriminates between the three cases that can occur.

 If b

− 4ac > 0 then there are two solutions

x = and x =

 If b

− 4ac = 0 then there is one solution

x =

 If b

− 4ac < 0 then there are no solutions because does not exist.

− 4ac)

−±

−b

−− −bbac

( )

−+ −bbac

( )

Practice Problem

2 Solve the following quadratic equations (where possible):

(a)

− 19x − 10 = 0 (b) 4x

+ 12x + 9 = 0

+ x + 1 = 0 (d) x

− 3x + 10 = 2x + 4

You may be familiar with another method for solving quadratic equations. This is based on

the factorization of a quadratic into the product of two linear factors. Section 1.4 described how

to multiply out two brackets. One of the examples in that section showed that

(x + 1)(x + 2) = x

+ 3x + 2

Consequently, the solutions of the equation

+ 3x + 2 = 0

MFE_C02a.qxd 16/12/2005 10:59 Page 119