Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

then the inputs K = 27 and L = 100 lead to an output

Q = 100(27)

1/3

(100)

1/2

= 100(3)(10)

= 3000

Of particular interest is the effect on output when inputs are scaled in some way. If capital and

labour both double, does the production level also double, does it go up by more than double

or does it go up by less than double? For the particular production function,

Q = 100K

1/3

1/2

we see that, when K and L are replaced by 2K and 2L, respectively,

Q = 100(2K)

1/3

(2L)

1/2

Now, by rule 4,

(2K)

1/3

= 2

1/3

and (2L)

1/2

= 2

1/2

Q = 100(2

1/3

)(2

1/2

)

= (2

1/3

1/2

)(100K

1/3

1/2

)

The second term, 100K

1/3

1/2

, is just the original value of Q, so we see that the output is

multiplied by

1/3

1/2

Using rule 1, this number may be simpliﬁed by adding the indices to get

1/3

1/2

= 2

5/6

Moreover, because 5/6 is less than 1, the scale factor is smaller than 2. In fact, my calculator gives

5/6

= 1.78 (to 2 decimal places)

so output goes up by just less than double.

Non-linear Equations

150

MFE_C02c.qxd 16/12/2005 11:00 Page 150

It is important to notice that the above argument does not depend on the particular value,

2, that is taken as the scale factor. Exactly the same procedure can be applied if the inputs, K

and L, are scaled by a general number λ (where λ is a Greek letter pronounced ‘lambda’).

Replacing K and L by λK and λL respectively in the formula

Q = 100K

1/3

1/2

gives

Q = 100(λK )

1/3

(λL)

1/2

= 100λ

1/3

1/2

(rule 4)

= (λ

1/3

1/2

)(100K

1/3

1/2

)

=λ

5/6

(100K

1/3

1/2

) (rule 1)

We see that the output gets scaled by λ

5/6

, which is smaller than λ since the power, 5/6, is less

than 1. We describe this by saying that the production function exhibits decreasing returns

to scale.

In general, a function

Q = f(K, L)

is said to be homogeneous if

f(λK, λL) =λ

f(K, L)

for some number, n. This means that when both variables K and L are multiplied by λ we can

pull out all of the λs as a common factor, λ

. The power, n, is called the degree of homo-

geneity. In the previous example we showed that

f(λK, λL) =λ

5/6

f(K, L)

and so it is homogeneous of degree 5/6. In general, if the degree of homogeneity, n, satisﬁes:

 n < 1, the function is said to display decreasing returns to scale

 n = 1, the function is said to display constant returns to scale

 n > 1, the function is said to display increasing returns to scale.

2.3 • Indices and logarithms

151

Example

Show that the following production function is homogeneous and ﬁnd its degree of homogeneity:

Q = 2K

1/2

3/2

Does this function exhibit decreasing returns to scale, constant returns to scale or increasing returns to

scale?

Solution

We are given that

f(K, L) = 2K

1/2

3/2

so replacing K by λK and L by λL gives

f(λK, λL) = 2(λK)

1/2

(λL)

3/2



MFE_C02c.qxd 16/12/2005 11:00 Page 151

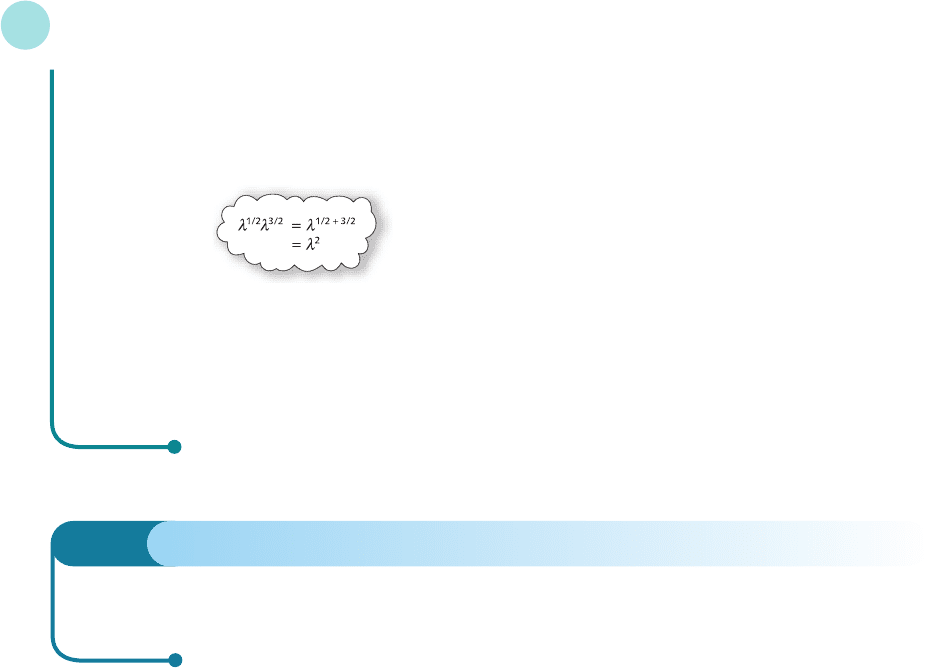
We can pull out all of the λs by using rule 4 to get

2λ

1/2

3/2

and then using rule 1 to get

(2K

1/2

3/2

)

We have therefore shown that

f(λK, λL) =λ

f(K, L)

and so the function is homogeneous of degree 2. Moreover, since 2 > 1 we deduce that it has increasing

returns to scale.

Non-linear Equations

152

Practice Problem

4 Show that the following production functions are homogeneous and comment on their returns to scale:

(a)

Q = 7KL

(b) Q = 50K

1/4

3/4

You may well have noticed that all of the production functions considered so far are of the

form

Q = AK

for some positive constants, A, α and β. (The Greek letters α and β are pronounced ‘alpha’ and

‘beta’ respectively.) Such functions are called Cobb–Douglas production functions. It is easy

to see that they are homogeneous of degree α+βbecause if

f(K, L) = AK

then

f(λK, λL) = A(λK)

(λL)

= Aλ

(rule 4)

=λ

α+β

(AK

) (rule 1)

=λ

α+β

f(K, L)

Consequently, Cobb–Douglas production functions exhibit

 decreasing returns to scale, if α+β<1

 constant returns to scale, if α+β=1

 increasing returns to scale, if α+β>1.

By the way, not all production functions are of this type. Indeed, it is not even necessary for

a production function to be homogeneous. Some examples illustrating these cases are given

MFE_C02c.qxd 16/12/2005 11:00 Page 152

2.3 • Indices and logarithms

153

Advice

Students have been known to regard logarithms as something rather abstract and difficult

to understand. There is, however, no need to worry about logarithms, since they simply

provide an alternative way of thinking about numbers such as b

. Read through the fol-

lowing example and try Practice Problem 5 for yourself. You might discover that they are

easier than you expect!

Example

Evaluate

(a) log

9 (b) log

2 (c) log

Solution

(a) To ﬁnd the value of log

9 we convert the problem into one involving powers. From the deﬁnition of a

logarithm to base 3 we see that the statement



in Practice Problems 13 and 14 at the end of this section. We shall return to the topic of pro-

duction functions in Chapter 5.

2.3.3 Logarithms

At the beginning of this section we stated that if a number, M, is expressed as

M = b

then b

is called the exponential form of M to base b. The approach taken so far has simply been

to evaluate M from any given values of b and n. In practice, it may be necessary to reverse this

process and to ﬁnd n from known values of M and b. To solve the equation

32 = 2

we need to express 32 as a power of 2. In this case it is easy to work out n by inspection. Simple

trial and error easily gives n = 5 because

= 32

We describe this expression by saying that the logarithm of 32 to base 2 is 5. In symbols we write

log

32 = 5

Quite generally,

if M

then log

when n is called the logarithm of M to base b.

MFE_C02c.qxd 16/12/2005 11:00 Page 153

log

9 = n

is equivalent to

9 = 3

The problem of ﬁnding the logarithm of 9 to base 3 is exactly the same as that of writing 9 as a power

of 3. The solution of this equation is clearly n = 2 since

9 = 3

Hence log

9 = 2.

(b) Again to evaluate log

2 we merely rewrite

log

2 = n

in exponential form as

2 = 4

The problem of ﬁnding the logarithm of 2 to base 4 is exactly the same as that of writing 2 as a power

of 4. The value of 2 is obtained from 4 by taking the square root, which involves raising 4 to the power

/2, so

2 = 4

1/2

Hence log

4 =

/2.

log

/7 = n

then

= 7

The value of

/7 is found by taking the reciprocal of 7, which involves raising 7 to the power of −1:

that is,

= 7

−1

Hence log

/7 =−1.

Non-linear Equations

154

Practice Problem

5 (1) Write down the values of n which satisfy

(a)

1000 = 10

(b) 100 = 10

(d) 1 = 10

(e) = 10

(f) = 10

(2) Use your answer to part (1) to write down the values of

(a)

log

1000 (b) log

100 (c) log

(d) log

1 (e) log

/10 (f) log

/100

(3) Confirm your answer to part (2) using a calculator.

100

MFE_C02c.qxd 16/12/2005 11:00 Page 154

2.3 • Indices and logarithms

155

Example

Use the rules of logarithms to express each of the following as a single logarithm:

(a) log

x + log

y − log

z (b) 2log

x − 3log

Solution

(a) The ﬁrst rule of logs shows that the sum of two logs can be written as the log of a product, so

log

x + log

y − log

z = log

(xy) − log

Also, according to rule 2, the difference of two logs is the log of a quotient, so we can simplify further to

get

log

(b) Given any combination of logs such as

2log

x − 3log



Given the intimate relationship between exponentials and logarithms, you should not be too

surprised to learn that logarithms satisfy three rules that are comparable with those for indices.

The rules of logarithms are as follows.

Rule 1 log

××

log

Rule 2 log

(x / y)

log

−−

log

Rule 3 log

mlog

A long time ago, before the pocket calculator was invented, people used tables of logarithms

to perform complicated arithmetic calculations. It was generally assumed that everyone could

add or subtract numbers using pen and paper, but that people found it hard to multiply and

divide. The ﬁrst two rules gave a means of converting calculations involving multiplication and

division into easier calculations involving addition and subtraction. For example, to work out

1.765 12 × 25.329 71

we would ﬁrst look up the logarithms of 1.765 12 and 25.329 71 using tables and then add these

logarithms together on paper. According to rule 1, the value obtained is just the logarithm

of the answer. Finally, using tables of antilogarithms (which in effect raised the base to

an appropriate power), the result of the calculation was obtained. Fortunately for us, this is all

history and we can now perform arithmetic calculations in a fraction of the time it took our

predecessors to multiply or divide two numbers. This might suggest that logarithms are redund-

ant. However, the idea of a logarithm remains an important one. The logarithm function

itself – that is,

f(x) = log

(x)

is of value and we shall investigate its properties later in the book. For the time being we ﬁrst

show how to use the laws of logarithms in algebra and then demonstrate how logarithms can

be used to solve algebraic equations in which the unknown appears as a power. This technique

will be of particular use in the next chapter when we solve compound interest problems.

MFE_C02c.qxd 16/12/2005 11:00 Page 155

the trick is to use the third rule to ‘get rid’ of the coefﬁcients. Since

2log

x = log

and 3log

y = log

we see that

2log

x − 3log

y = log

− log

Only now can we use the second rule of logs, which allows us to write the expression as the single

logarithm

log

Non-linear Equations

156

Example

Find the value of x which satisﬁes

(a) 200(1.1)

= 20 000 (b) 5

= 2(3)

Solution

(a) An obvious ﬁrst step in the solution of

200(1.1)

= 20 000

is to divide both sides by 200 to get

(1.1)

= 100

In Chapter 1 it was pointed out that we can do whatever we like to an equation, provided that we do

the same thing to both sides. In particular, we may take logarithms of both sides to get

log(1.1)

= log(100)

Now by rule 3 we have

log(1.1)

= xlog(1.1)

so the equation becomes

xlog(1.1) = log(100)

Notice the effect that rule 3 has on the equation. It brings the unknown down to the same level as the

rest of the expression. This is the whole point of taking logarithms, since it converts an equation in

which the unknown appears as a power into one which can be solved using familiar algebraic methods.

Dividing both sides of the equation

xlog(1.1) = log(100)

by log(1.1) gives

Practice Problem

6 Use the rules of logs to express each of the following as a single logarithm:

(a)

log

x − log

y + log

z (b) 4log

x + 2log

MFE_C02c.qxd 16/12/2005 11:00 Page 156

x =

So far no mention has been made of the base of the logarithm. The above equation for x is true no mat-

ter what base is used. It makes sense to use logarithms to base 10 because all scientiﬁc calculators have

this facility as one of their function keys. Using base 10, my calculator gives

x == =48.32

to 2 decimal places.

As a check, if this number is substituted back into the original equation, then

200(1.1)

= 200(1.1)

48.32

= 20 004 ✓

We cannot expect to obtain the exact answer, because we rounded x to only two decimal places.

(b) To solve

= 2(3)

we take logarithms of both sides to get

log(5

) = log(2 × 3

)

The right-hand side is the logarithm of a product and, according to rule 1, can be written as the sum of

the logarithms, so the equation becomes

log(5

) = log(2) + log(3

)

As in part (a) the key step is to use rule 3 to ‘bring down the powers’. If rule 3 is applied to both log(5

)

and log(3

) then the equation becomes

xlog(5) = log(2) + xlog(3)

This is now the type of equation that we know how to solve. We collect x’s on the left-hand side to get

xlog(5) − xlog(3) = log(2)

and then pull out a common factor of x to get

x[log(5) − log(3)] = log(2)

Now, by rule 2, the difference of two logarithms is the same as the logarithm of their quotient, so

log(5) − log(3) = log(5 ÷ 3)

Hence the equation becomes

xlog = log(2)

x =

Finally, taking logarithms to base 10 using a calculator gives

x ==1.36

to 2 decimal places.

0.301 029 996

0.221 848 750

log(2)

log(5/3)

0.041 392 685

log(100)

log(1.1)

log(100)

log(1.1)

2.3 • Indices and logarithms

157



MFE_C02c.qxd 16/12/2005 11:00 Page 157

As a check, the original equation

= 2(3)

becomes

1.36

= 2(3)

1.36

that is,

8.92 = 8.91 ✓

Again the slight discrepancy is due to rounding errors in the value of x.

Non-linear Equations

158

Practice Problem

7 Solve the following equations for x:

(a)

= 7 (b) 5(2)

= 10

Advice

In this section we have met a large number of definitions and rules concerning indices and

logarithms. For convenience, we have collected these together in the form of a summary.

The facts relating to indices are particularly important and you should make every effort

to memorize these before proceeding with the rest of this book.

2.3.4 Summary

Indices

If n is a positive whole number then

= b × b × ...× b

= 1

−n

= 1/b

1/n

= nth root of b

Also, if p and q are whole numbers with q > 0 then

p/q

= (b

)

1/q

= (b

1/q

)

The four rules of indices are:

Rule 1 b

× b

= b

m+n

Rule 2 b

÷ b

= b

m−n

Rule 3 (b

)

= b

Rule 4 (ab)

= a

MFE_C02c.qxd 16/12/2005 11:00 Page 158

Logarithms

If M = b

then n = log

M. The three rules of logarithms are:

Rule 1 log

(x × y) = log

x + log

Rule 2 log

(x ÷ y) = log

x − log

Rule 3 log

= mlog

2.3 • Indices and logarithms

159

Capital Man-made assets used in the production of goods and services.

Cobb–Douglas production function A production function of the form: Q = AK

Constant returns to scale Exhibited by a production function when a given percentage

increase in input leads to the same percentage increase in output: f(

L) =

f(K, L).

Decreasing returns to scale Exhibited by a production function when a given percentage

increase in input leads to a smaller percentage increase in output: f(

L) =

f(K, L)

where 0 < n < 1.

Exponent A superscript attached to a variable; the number 5 is the exponent in the

expression, 2x

Exponential form A representation of a number which is written using powers. For

example, 2

is the exponential form of the number 32.

Factors of production The inputs into the production of goods and services: labour, land,

capital and raw materials.

Homogeneous functions A function with the property that when all of the inputs are multi-

plied by a constant,

, the output is multiplied by

where n is the degree of homogeneity.

Increasing returns to scale Exhibited by a production function when a given percentage

increase in input leads to a larger percentage increase in output: f(

L) =

f(K, L) where

Index Another word for exponent.

Labour All forms of human input to the production process.

Logarithm The power to which a base must be raised to yield a particular number.

Power Another word for exponent. If this is a positive integer then it gives the number of

times a number is multiplied by itself.

Production function The relationship between the output of a good and the inputs used

to produce it.

Key Terms

Practice Problems

(1) Without using your calculator evaluate

(a)

(b) 2

−1

(d) 17

(e) 1

1/5

(f) 36

1/2

(g) 8

2/3

(h) 49

−3/2

(2) Confirm your answer to part (1) using a calculator.

9 Evaluate the following without using a calculator

(a)

3/5

(b) 64

−5/6

(c)

−4/3

(d) 3

2/3

(e) 2

−1/2

125



MFE_C02c.qxd 16/12/2005 11:00 Page 159