Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

Non-linear Equations

170

Advice

The following example shows how to find such a formula from data points. This is an

important skill. However, it is not crucial to your understanding of subsequent material in

this book. You may wish to miss this out on first reading and move straight on to the

Practice Problems at the end of this chapter.

Example

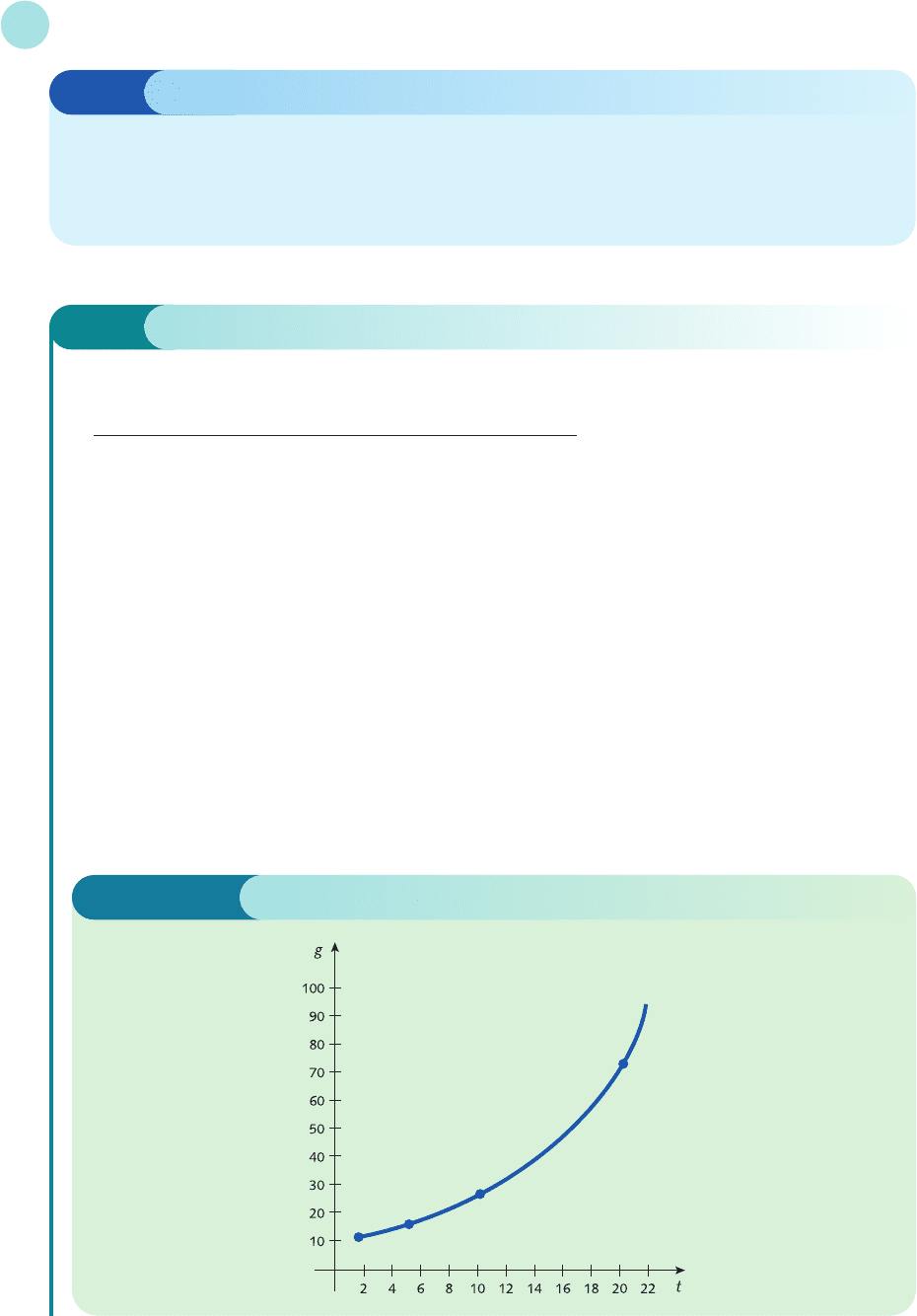
The values of GNP, g, measured in billions of dollars, over a period of t years was observed to be

t (years) 2 5 10 20

g (billions of dollars) 12 16 27 74

Model the growth of GNP using a formula of the form

g = Be

for appropriate values of A and B. Hence estimate the value of GNP after 15 years.

Solution

Figure 2.17 shows the four points plotted with g on the vertical axis and t on the horizontal axis. The basic

shape of the curve joining these points certainly suggests that an exponential function is likely to provide a

reasonable model, but it gives no information about what values to use for the parameters A and B.

However, since one of the unknown parameters, A, occurs as a power in the relation

g = Be

it is a good idea to take natural logs of both sides to get

ln g = ln(Be

)

Figure 2.17

MFE_C02d.qxd 16/12/2005 11:01 Page 170

The rules of logs enable us to expand the right-hand side to get

ln (Be

) = ln B + ln(e

) (rule 1)

= ln B + At (deﬁnition of a log to base e)

Hence

ln g = At + ln B

Although this does not look like it at ﬁrst sight, this relation is actually the equation of a straight line! To see

this recall that the usual equation of a line is y = ax + b. The log equation is indeed of this form if we put

y = ln g and x = t

The equation then becomes

y = Ax + ln B

so a graph of ln g plotted on the vertical axis with t plotted on the horizontal axis should produce a straight

line with slope A and with an intercept on the vertical axis of ln B.

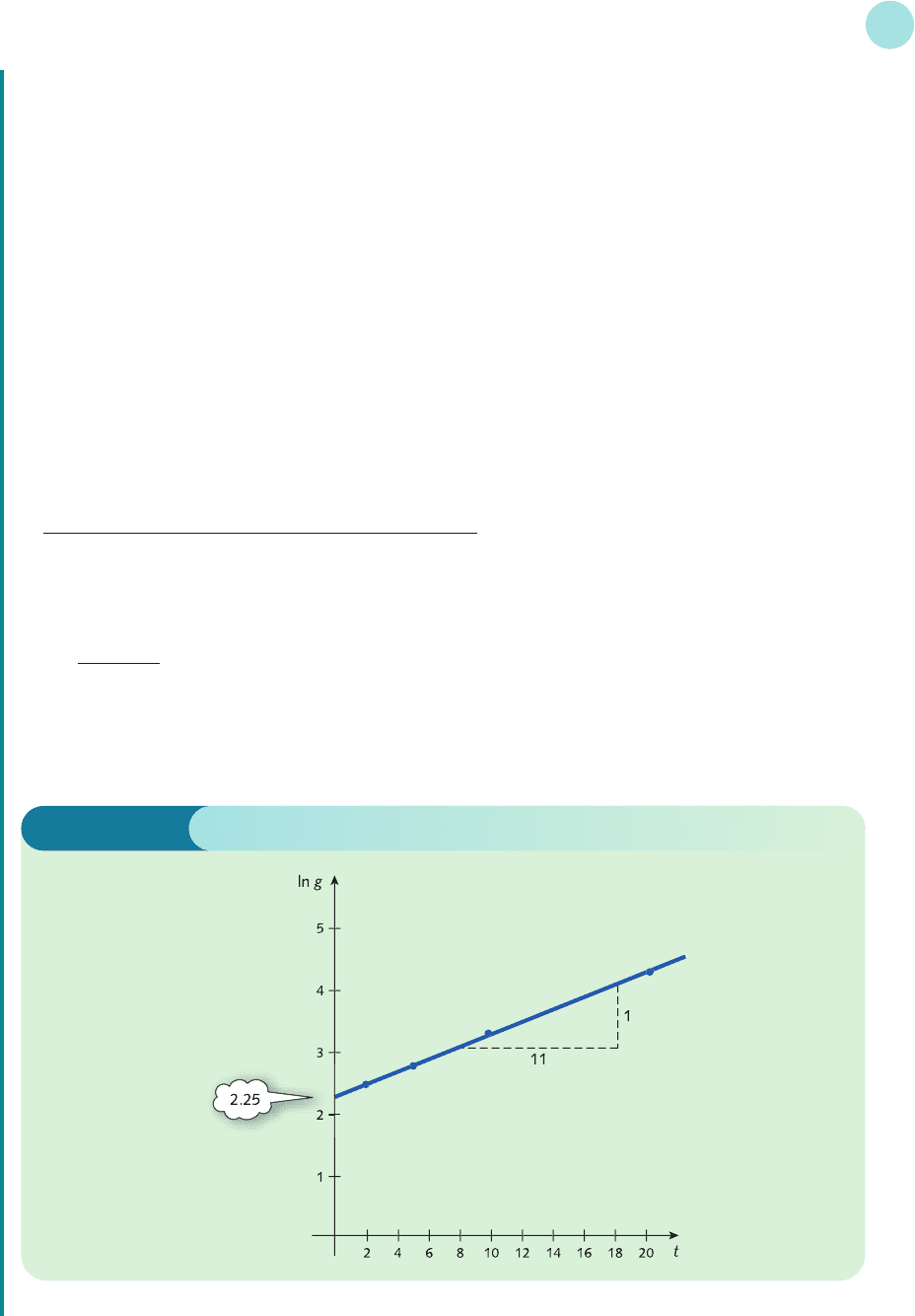
Figure 2.18 shows this graph based on the table of values

x = t 251020

y = ln g 2.48 2.77 3.30 4.30

As one might expect, the points do not exactly lie on a straight line, since the formula is only a model.

However, the line sketched in Figure 2.18 is a remarkably good ﬁt. The slope can be calculated as

A ==0.09

and the vertical intercept can be read off the graph as 2.25. This is ln B and so

B = e

2.25

= 9.49

4 − 3

18.6 − 7.6

2.4 • The exponential and natural logarithm functions

171

Figure 2.18



MFE_C02d.qxd 16/12/2005 11:01 Page 171

Hence the formula for the approximate relation between g and t is

g = 9.49e

0.09t

Finally, an estimate of the GNP after 15 years can be obtained by substituting t

15 into this formula to get

g = 36.6 (billion dollars)

Non-linear Equations

172

Practice Problem

6 Immediately after the launch of a new product, the monthly sales figures (in thousands) are as follows:

t (months) 13612

s (sales) 1.8 2.7 5.0 16.5

(1) Complete the following table of values of ln s

t 13612

ln s 0.59 1.61

(2) Plot these points on graph paper with the values of ln s on the vertical axis and t on the horizontal

axis. Draw a straight line passing close to these points. Write down the value of the vertical inter-

cept and calculate the slope.

(3) Use your answers to part (2) to estimate the values of A and B in the relation s = Be

(4) Use the exponential model derived in part (3) to estimate the sales when

(a) t = 9 (b) t = 60

Which of these estimates would you expect to be the more reliable? Give a reason for your answer.

The exponential function The function, f(x) = e

; an exponential function in which the

base is number, e = 2.718 28...

Natural logarithm A logarithm to base, e; if M = e

then n is the natural logarithm of M

and we write, n = ln M

Key Terms

Practice Problems

7 The number of items, N, produced each day by an assembly-line worker, t days after an initial train-

ing period, is modelled by

N = 100 − 100e

−0.4t

(1) Calculate the number of items produced daily

(a) 1 day after the training period

(b) 2 days after the training period

MFE_C02d.qxd 16/12/2005 11:01 Page 172

(2) What is the worker’s daily production in the long run?

(3) Sketch a graph of N against t and explain why the general shape might have been expected.

8 Use the rules of logs to expand each of the following:

(a)

ln xy (b) ln xy

(d) ln (e) ln (f) ln

9 Use the rules of logs to express each of the following as a single logarithm:

(a)

ln x + 2 ln x (b) 4 ln x − 3 ln y + 5 ln z

10 Solve each of the following equations. (Round your answer to 2 decimal places.)

(a)

= 5.9 (b) e

= 0.45 (c) e

=−2

(d) e

= 13.68 (e) e

−5x

= 0.34 (f) 4e

= 7.98

11 The value of a second-hand car reduces exponentially with age, so that its value $y after t years can

be modelled by the formula

y = Ae

−ax

If the car was $50 000 when new and was worth $38 000 after 2 years, find the values of A and a,

correct to 3 decimal places.

Use this model to predict the value of the car

(a) when the car is 5 years old

(b) in the long run

12 A team of financial advisers guiding the launch of a national newspaper has modelled the future

circulation of the newspaper by the equation

N = c(1 − e

−kt

)

where N is the daily circulation after t days of publication, and c and k are positive constants.

Transpose this formula to show that

t = ln

When the paper is launched, audits show that

c = 700 000 and k = ln 2

(a) Calculate the daily circulation after 30 days of publication.

(b) After how many days will the daily circulation first reach 525 000?

only if the daily circulation exceeds 750 000?

13 A Cobb–Douglas production function is given by

Q = 3L

1/2

1/3

By taking logs of both sides of this equation, show that

ln Q = ln 3 + ln L + ln K

If a graph were to be sketched of ln Q against ln K (for varying values of Q and K but with L fixed),

explain briefly why the graph will be a straight line and state its slope and vertical intercept.

c − N

2.4 • The exponential and natural logarithm functions

173



MFE_C02d.qxd 16/12/2005 11:01 Page 173

14 The following table gives data relating a firm’s output, Q and labour, L.

L 12345

Q 0.50 0.63 0.72 0.80 0.85

The firm’s short-run production function is believed to be of the form

Q = AL

(a) Show that

ln Q = n ln L + ln A

(b) Using the data supplied, copy and complete the following table:

ln L 0.69 1.39

ln Q −0.69 −0.33 −0.16

Plot these points with ln L on the horizontal axis and ln Q on the vertical axis. Draw a straight

line passing as close as possible to all five points.

the parameters n and A.

15 (Excel) Tabulate values of the following functions for x = 0, 0.2, 0.4, ..., 2. Hence sketch graphs of

these functions, on the same diagram, over the range 0 ≤ x ≤ 2. Discuss, in qualitative terms, any dif-

ferences or similarities between these functions.

(a)

y = x (b) y = x

(d) y =√x (e) y = e

[In Excel, e

is typed EXP(x)]

(Excel) Tabulate values of the functions ln x, log

x and log

x for x = 0.2, 0.4, 0.6, 0.8, 1.0, 2, 3, 4,

..., 8. Hence sketch graphs of these functions on the same diagram, over the range 0.2 ≤ x ≤ 8.

Briefly comment on any similarities and differences between them.

[In Excel, natural logs and logs to base 10 are typed as LN(x) and LOG(x) respectively. In general,

to find the logarithm of a number x to base n, type LOG(x, n)]

(Excel) The demand function of a good can be modelled approximately by

P = 100 − Q

(a) Show that if this relation is exact then a graph of ln(150 − 1.5P) against ln Q will be a straight

line passing through the origin with slope n.

(b) For the data given below, tabulate the values of ln(150 − 1.5P) and ln Q. Find the line of best fit

and hence estimate the value of n correct to 1 decimal place.

Q 10 50 60 100 200 400

P 95 85 80 70 50 20

Non-linear Equations

174

MFE_C02d.qxd 16/12/2005 11:01 Page 174

chapter 3

Mathematics of Finance

This chapter provides an understanding of the way in which financial calculations are

worked out. There are four sections, which should be read in the order that they

appear.

Section 3.1 revises work on percentages. In particular, a quick method of dealing

with percentage increase and decrease calculations is described. This enables an

overall percentage change to be deduced easily from a sequence of individual

changes. Percentages are used to calculate and interpret index numbers, and to

adjust value data for inflation.

Section 3.2 shows how to calculate the future value of a lump sum which is invested

to earn interest. This interest can be added to the investment annually, semi-annu-

ally, quarterly or even more frequently. The exponential function is used to solve

problems in which interest is compounded continuously.

A wide variety of applications are considered in Sections 3.3 and 3.4. In Section 3.3

a mathematical device known as a geometric progression, which is used to calculate

the future value of a savings plan and the monthly repayments of a loan, is intro-

duced. Section 3.4 describes the opposite problem of calculating the present value

given a future value. The process of working backwards is called discounting. It can

be used to decide how much money to invest today in order to achieve a specific

target sum in a few years’ time. Discounting can be used to appraise different invest-

ment projects. On the macroeconomic level, the relationship between interest rates

and speculative demand for money is investigated.

The material in this chapter will be of greatest benefit to students on business stud-

ies and accountancy courses. This chapter could be omitted without affecting your

understanding of the rest of this book.

MFE_C03a.qxd 16/12/2005 11:02 Page 175

MFE_C03a.qxd 16/12/2005 11:02 Page 176

section 3.1

Percentages

In order to be able to handle ﬁnancial calculations, it is necessary to use percentages proﬁci-

ently. The word ‘percentage’ literally means ‘per cent’, i.e. per hundredth, so that whenever we

speak of r% of something, we simply mean the fraction (r/100)ths of it.

Objectives

At the end of this section you should be able to:

 Understand what a percentage is.

 Solve problems involving a percentage increase or decrease.

 Write down scale factors associated with percentage changes.

 Work out overall percentage changes.

 Calculate and interpret index numbers.

 Adjust value data for inﬂation.

Advice

The first part of this section provides a leisurely revision of the idea of a percentage as

well as reminding you about how to use scale factors to cope with percentage changes.

These ideas are crucial to any understanding of financial mathematics. However, if you are

already confident in using percentages, you may wish to miss this out and move straight

on to the applications covered in sub-sections 3.1.1 and 3.1.2.

MFE_C03a.qxd 16/12/2005 11:02 Page 177

For example,

25% is the same as =

30% is the same as =

50% is the same as =

100

Mathematics of Finance

178

Example

Calculate

(a) 15% of 12 (b) 98% of 17 (c) 150% of 290

Solution

(a) 15% of 12 is the same as

× 12 = 0.15 × 12 = 1.8

(b) 98% of 17 is the same as

× 17 = 0.98 × 17 = 16.66

× 290 = 1.5 × 290 = 435

150

100

Practice Problem

1 Calculate

(a) 10% of $2.90 (b) 75% of $1250 (c) 24% of $580

Whenever any numerical quantity increases or decreases, it is customary to refer to this

change in percentage terms. The following example serves to remind you how to perform cal-

culations involving percentage changes.

Example

(a) An investment rises from $2500 to $3375. Express the increase as a percentage of the original.

(b) At the beginning of a year, the population of a small village is 8400. If the annual rise in population is

12%, ﬁnd the population at the end of the year.

MFE_C03a.qxd 16/12/2005 11:02 Page 178

Solution

(a) The rise in the value of the investment is

3375 − 2500 = 875

As a fraction of the original this is

= 0.35

This is the same as 35 hundredths, so the percentage rise is 35%.

(b) As a fraction

12% is the same as = 0.12

so the rise in population is

0.12 × 8400 = 1008

Hence the ﬁnal population is

8400 + 1008 = 9408

20% is the same as = 0.2

so the fall in price is

0.2 × 580 = 116

Hence the ﬁnal price is

580 − 116 = $464

100

875

2500

3.1 • Percentages

179

Practice Problem

2 (a) A firm’s annual sales rise from 50 000 to 55 000 from one year to the next. Express the rise as a

percentage of the original.

(b) The government imposes a 15% tax on the price of a good. How much does the consumer pay

for a good priced by a firm at $1360?

the year if it was worth $9500 at the beginning of the year.

In the previous example and in Practice Problem 2, the calculations were performed in two

separate stages. The actual rise or fall was ﬁrst worked out, and these changes were then applied to

the original value to obtain the ﬁnal answer. It is possible to obtain this answer in a single calcula-

tion, and we now describe how this can be done. Not only is this new approach quicker, but it

also enables us to tackle more difﬁcult problems. To be speciﬁc, let us suppose that the price

of good is set to rise by 9%, and that its current price is $78. The new price consists of the

MFE_C03a.qxd 16/12/2005 11:02 Page 179