Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

10 Use the rules of indices to simplify

(a)

3/2

× y

1/2

(b) (c) (xy

1/2

)

(d) ( p

)

1/3

÷ ( p

1/3

)

(e) (24q)

1/3

÷ (3q)

1/3

(f) (25p

)

1/2

11 Write the following expressions using index notation

(a) (b)

5√x (c) (d) 2x √x (e)

12 For the production function, Q = 200K

1/4

2/3

find the output when

(a)

16, L = 27 (b) K

10 000, L = 1000

13 Which of the following production functions are homogeneous? For those functions which are homo-

geneous write down their degrees of homogeneity and comment on their returns to scale.

(a)

Q = 500K

1/3

1/4

(b) Q = 3LK + L

14 Show that the production function

Q = A[bK

+ (1 − b)L

]

is homogeneous and displays constant returns to scale.

15 Write down the values of x which satisfy each of the following equations:

(a)

= 25 (b) 3

= (c) 2

(d) 2

= 64 (e) 100

= 10 (f) 8

= 16

16 Solve the following equations:

(a)

= 4 (b) 4 × 2

= 32 (c) 8

= 2 ×

17 Write down the value of

(a)

log

(b) log

b (c) log

1 (d) log

√b (e) log

(1/b)

18 Use the rules of logs to express each of the following as a single log:

(a)

log

(xy) − log

x − log

(b) 3log

x − 2log

y + 5log

x − 2log

19 Express the following in terms of log

x, log

y and log

(a)

log

)

(b) log

20 If log

2 = p, log

3 = q and log

10 = r, express the following in terms of p, q and r:

(a)

log

(b) log

12 (c) log

0.0003 (d) log

600

√

−1

Non-linear Equations

160

MFE_C02c.qxd 16/12/2005 11:00 Page 160

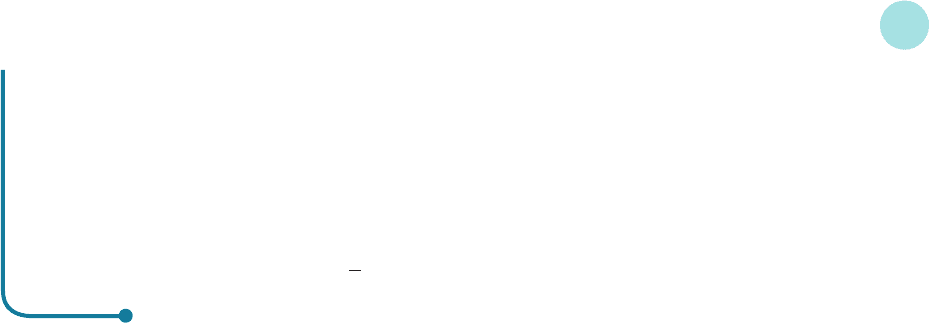
21 Solve the following equations:

(a)

10(1.07)

= 2000 (b) 10

x−1

= 3 (c) 5

x−2

= 5 (d) 2(7)

−x

= 3

22 Solve the inequalities

(a)

2x+1

≤ 7 (b) 0.8

< 0.04

23 Solve the equation

log

(x + 2) + log

x − 1 = log

2.3 • Indices and logarithms

161

MFE_C02c.qxd 16/12/2005 11:00 Page 161

section 2.4

The exponential and natural

logarithm functions

In the previous section we described how to deﬁne numbers of the form b

, and discussed the

idea of a logarithm, log

x. It turns out that there is one base (the number e = 2.718 281...)

that is particularly important in mathematics. The purpose of this present section is to intro-

duce you to this strange number and to consider a few simple applications.

Objectives

At the end of this section you should be able to:

 Sketch graphs of general exponential functions.

 Understand how the number e is deﬁned.

 Use the exponential function to model growth and decay.

 Use log graphs to ﬁnd unknown parameters in simple models.

 Use the natural logarithm function to solve equations.

Example

Sketch the graphs of the functions

(a) f(x) = 2

(b) g(x) = 2

−x

Comment on the relationship between these graphs.

Solution

(a) As we pointed out in Section 2.3, a number such as 2

is said to be in exponential form. The number 2 is

called the base and x is called the exponent. Values of this function are easily found either by pressing

the power key on a calculator or by using the deﬁnition of b

given in Section 2.3. A selection of

these are given in the following table:

MFE_C02d.qxd 16/12/2005 11:01 Page 162

x −3 −2 −10123 4 5

0.125 0.25 0.512481632

A graph of f(x) based on this table is sketched in Figure 2.14. Notice that the graph approaches the

x axis for large negative values of x and it rises rapidly as x increases.

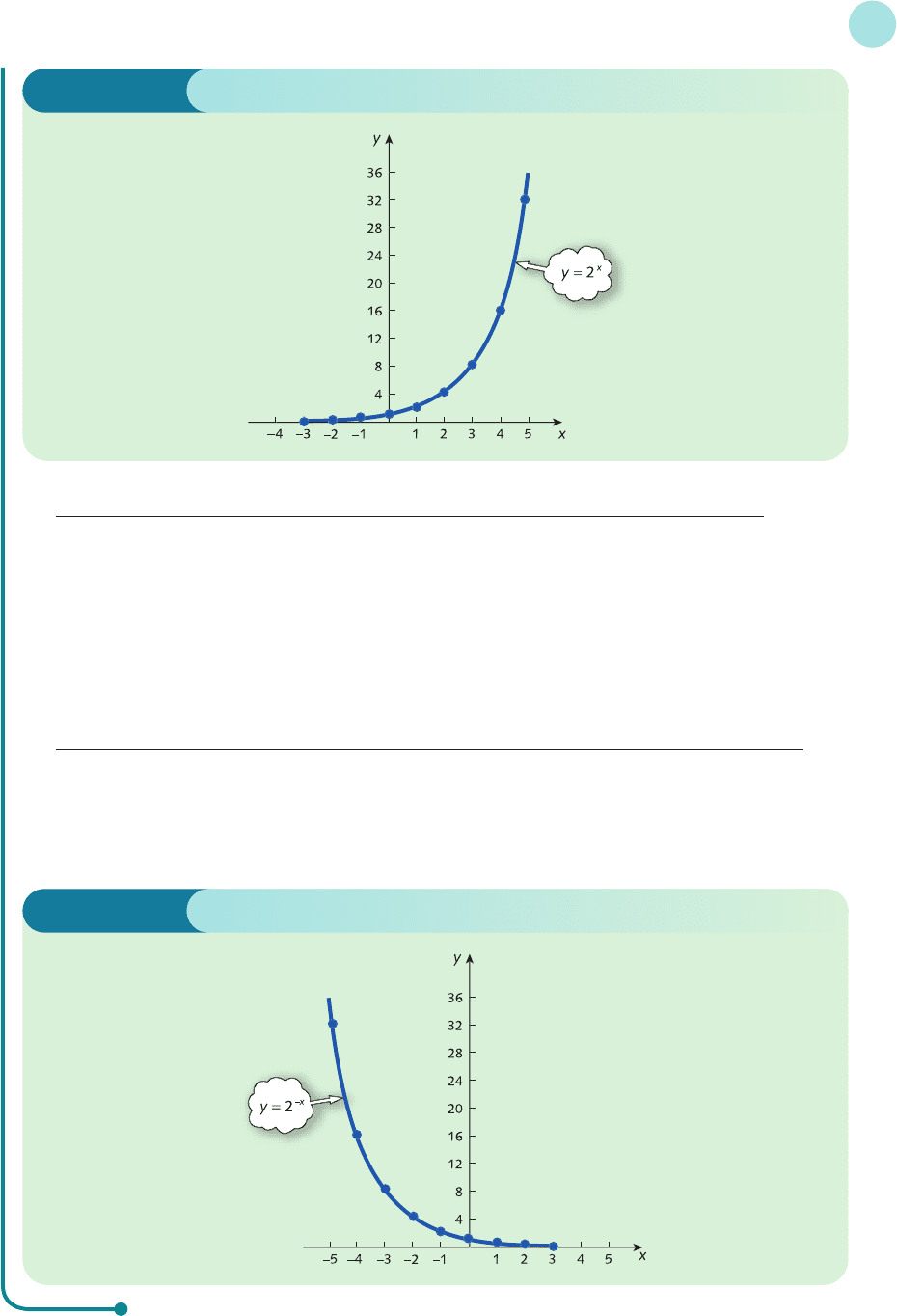
(b) The negative exponential

g(x) = 2

−x

has values

x −5 −4 −3 −2 −101 2 3

−x

32 16 8 4 2 1 0.5 0.25 0.125

This function is sketched in Figure 2.15. It is worth noticing that the numbers appearing in the table

of 2

−x

are the same as those of 2

but arranged in reverse order. Hence the graph of 2

−x

is obtained by

reﬂecting the graph of 2

in the y axis.

2.4 • The exponential and natural logarithm functions

163

Figure 2.14

Figure 2.15

MFE_C02d.qxd 16/12/2005 11:01 Page 163

Figure 2.14 displays the graph of a particular exponential function, 2

. Quite generally, the

graph of any exponential function

f(x) = b

has the same basic shape provided b > 1. The only difference is that larger values of b produce

steeper curves. A similar comment applies to the negative exponential, b

−x

Non-linear Equations

164

Practice Problem

1 Complete the following table of function values of 3

and 3

−x

and hence sketch their graphs.

x −3 −2 −10123

−x

Obviously there is a whole class of functions, each corresponding to a different base, b. Of

particular interest is the case when b takes the value

2.718 281 828 459...

This number is written as e and the function

f(x) = e

is referred to as the exponential function. In fact, it is not necessary for you to understand where

this number comes from. All scientiﬁc calculators have an e

button and you may simply wish

to accept the results of using it. However, it might help your conﬁdence if you have some

appreciation of how it is deﬁned. To this end consider the following example and sub-

sequent problem.

Example

Evaluate the expression

1 +

where m = 1, 10, 100 and 1000, and comment brieﬂy on the behaviour of this sequence.

Solution

Substituting the values m = 1, 10, 100 and 1000 into

1 +

gives

1 +

= 2

1 +

= (1.1)

= 2.593 742 460

MFE_C02d.qxd 16/12/2005 11:01 Page 164

1 +

100

= (1.01)

100

= 2.704 813 829

1 +

1000

= (1.001)

1000

= 2.716 923 932

The numbers are clearly getting bigger as m increases. However, the rate of increase appears to be slowing

down, suggesting that numbers are converging to some ﬁxed value.

1000

100

2.4 • The exponential and natural logarithm functions

165

The following problem gives you an opportunity to continue the sequence and to discover

for yourself the limiting value.

Practice Problem

2 (a) Use the power key x

on your calculator to evaluate

1 +

where m = 10 000, 100 000 and 1 000 000.

(b) Use your calculator to evaluate e

and compare with your answer to part (a).

Hopefully, the results of Practice Problem 2 should convince you that as m gets larger, the

value of

1 +

approaches a limiting value of 2.718 281 828..., which we choose to denote by the letter e. In

symbols we write

e = lim

m→∞

1 +

The signiﬁcance of this number can only be fully appreciated in the context of calculus,

which we study in Chapter 4. However, it is useful at this stage to consider some preliminary

examples. These will give you practice in using the e

button on your calculator and will give

you some idea how this function can be used in modelling.

Advice

The number e has a similar status in mathematics as the number

and is just as useful. It

arises in the mathematics of finance, which we discuss in the next chapter. You might like

to glance through Section 3.2 now if you need convincing of the usefulness of e.

Example

The percentage, y, of households possessing refrigerators, t years after they have been introduced in a

developed country, is modelled by

y = 100 − 95e

−0.15t



MFE_C02d.qxd 16/12/2005 11:01 Page 165

(1) Find the percentage of households that have refrigerators

(a) at their launch

(b) after 1 year

(d) after 20 years

(2) What is the market saturation level?

(3) Sketch a graph of y against t and hence give a qualitative description of the growth of refrigerator

ownership over time.

Solution

(1) To calculate the percentage of households possessing refrigerators now and in 1, 10 and 20 years’ time,

we substitute t = 0, 1, 10 and 20 into the formula

y = 100 − 95e

−0.15t

to get

(a) y(0) = 100 − 95e

= 5%

(b) y(1) = 100 − 95e

−0.15

= 18%

−1.5

= 79%

(d) y(20) = 100 − 95e

−3.0

= 95%

(2) To ﬁnd the saturation level we need to investigate what happens to y as t gets ever larger. We know that

the graph of a negative exponential function has the basic shape shown in Figure 2.15. Consequently,

the value of e

−0.15t

will eventually approach zero as t increases. The market saturation level is therefore

given by

y = 100 − 95(0) = 100%

Non-linear Equations

166

MFE_C02d.qxd 16/12/2005 14:34 Page 166

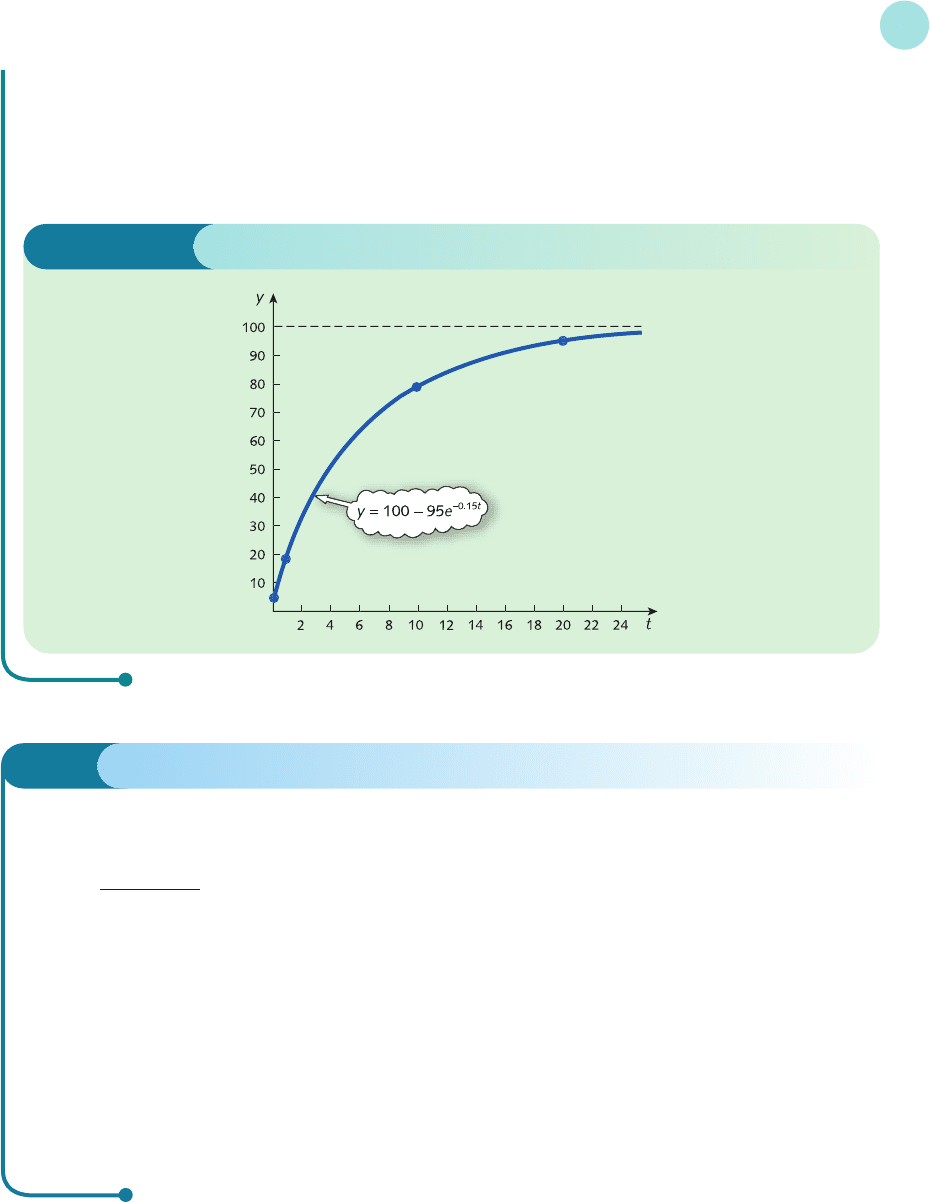
(3) A graph of y against t, based on the information obtained in parts (1) and (2), is sketched in Figure 2.16.

This shows that y grows rapidly to begin with, but slows down as the market approaches satura-

tion level. A saturation level of 100% indicates that eventually all households are expected to possess

refrigerators, which is not surprising given the nature of the product.

2.4 • The exponential and natural logarithm functions

167

Practice Problem

3 The percentage, y, of households possessing camcorders t years after they have been launched is

modelled by

y =

(1) Find the percentage of households that have camcorders

(a) at their launch

(b) after 10 years

(d) after 30 years

(2) What is the market saturation level?

(3) Sketch a graph of y against t and hence give a qualitative description of the growth of camcorder

ownership over time.

1 + 800e

−0.3t

In Section 2.3 we noted that if a number M can be expressed as b

then n is called the

logarithm of M to base b. In particular, for base e,

if M = e

then n = log

Figure 2.16

MFE_C02d.qxd 16/12/2005 11:01 Page 167

Non-linear Equations

168

Example

Use the rules of logs to express

(a) ln in terms of ln x and ln y

(b) 3 ln p + ln q − 2 ln r as a single logarithm

Solution

(a) In this part we need to ‘expand’, so we read the rules of logs from left to right:

ln = ln x − ln √y (rule 2)

= ln x − ln y

1/2

(fractional powers denote roots)

= ln x − ln y (rule 3)

(b) In this part we need to reverse this process and so read the rules from right to left:

3 ln p + ln q − 2 ln r = ln p

+ ln q − ln r

(rule 3)

= ln(p

q) − ln r

(rule 1)

= ln (rule 2)

√

Practice Problem

4 Use the rules of logs to express

(a) ln (a

) in terms of ln a and ln b

(b)

/2 ln x − 3 ln y as a single logarithm

As we pointed out in Section 2.3, logs are particularly useful for solving equations in which

the unknown occurs as a power. If the base is the number e then the equation can be solved by

using natural logarithms.

We call logarithms to base e natural logarithms. These occur sufﬁciently frequently to warrant

their own notation. Rather than writing log

M we simply put ln M instead. The three rules of

logs can then be stated as

Rule 1 ln (x

××

ln x

ln y

Rule 2 ln (x / y)

ln x

−−

ln y

Rule 3 ln x

m ln x

MFE_C02d.qxd 16/12/2005 11:01 Page 168

One important (but rather difﬁcult) problem in modelling is to extract a mathematical

formula from a table of numbers. If this relationship is of the form of an exponential then it is

possible to estimate values for some of the parameters involved.

2.4 • The exponential and natural logarithm functions

169

Practice Problem

5 During a recession a firm’s revenue declines continuously so that the revenue, TR (measured in millions

of dollars), in t years’ time is modelled by

TR = 5e

−0.15t

(a) Calculate the current revenue and also the revenue in 2 years’ time.

(b) After how many years will the revenue decline to $2.7 million?

Example

An economy is forecast to grow continuously so that the gross national product (GNP), measured in

billions of dollars, after t years is given by

GNP = 80e

0.02t

After how many years is GNP forecast to be $88 billion?

Solution

We need to solve

88 = 80e

0.02t

for t. Dividing through by 80 gives

1.1 = e

0.02t

Using the deﬁnition of natural logarithms we know that

if M = e

then n = ln M

If we apply this deﬁnition to the equation

1.1 = e

0.02t

we deduce that

0.02t = ln 1.1 = 0.095 31... (check this using your own calculator)

t ==4.77

We therefore deduce that GNP reaches a level of $88 billion after 4.77 years.

0.095 31

0.02

MFE_C02d.qxd 16/12/2005 11:01 Page 169