Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

original (which can be thought of as 100% of the $78) plus the increase (which is 9% of $78).

The ﬁnal price is therefore

100% + 9% = 109% (of the $78)

which is the same as

= 1.09

In other words, in order to calculate the ﬁnal price all we have to do is to multiply by the scale

factor, 1.09. Hence the new price is

1.09 × 78 = $85.02

One advantage of this approach is that it is then just as easy to go backwards and work out

the original price from the new price. To go backwards in time we simply divide by the scale

factor. For example, if the ﬁnal price of a good is $1068.20 then before a 9% increase the price

would have been

1068.20 ÷ 1.09 = $980

In general, if the percentage rise is r% then the ﬁnal value consists of the original (100%)

together with the increase (r%), giving a total of

+=1 +

To go forwards in time we multiply by this scale factor, whereas to go backwards we divide.

100

109

100

Mathematics of Finance

180

Example

(a) If the annual rate of inﬂation is 4%, ﬁnd the price of a good at the end of a year if its price at the

beginning of the year is $25.

(b) The cost of a good is $799 including 17.5% VAT (value added tax). What is the cost excluding VAT?

Solution

(a) The scale factor is

1 +=1.04

We are trying to ﬁnd the price after the increase, so we multiply to get

25 × 1.04 = $26

(b) The scale factor is

1 += 1.175

This time we are trying to ﬁnd the price before the increase, so we divide by the scale factor to get

799 ÷ 1.175 = $680

17.5

100

MFE_C03a.qxd 16/12/2005 11:02 Page 180

==1.06

which can be thought of as

1 +

so the rise is 6%.

100

1007

950

new value

old value

3.1 • Percentages

181

Example

(a) The value of a car depreciates by 25% in a year. What will a car, currently priced at $43 000, be worth

in a year’s time?

(b) After a 15% reduction in a sale, the price of a good is $39.95. What was the price before the sale began?

Solution

(a) The scale factor is

1 −=0.75

100

It is possible to use scale factors to solve problems involving percentage decreases. To be

speciﬁc, suppose that an investment of $76 falls by 20%. The new value is the original (100%)

less the decrease (20%), so is 80% of the original. The scale factor is therefore 0.8, giving a new

value of

0.8 × 76 = $60.80

In general, the scale factor for an r% decrease is

−=1 −

Once again, you multiply by this scale factor when going forwards in time and divide when

going backwards.

100

Practice Problem

3 (a) The value of a good rises by 13% in a year. If it was worth $6.5 million at the beginning of the

year, find its value at the end of the year.

(b) The GNP of a country has increased by 63% over the past 5 years and is now $124 billion. What

was the GNP 5 years ago?



MFE_C03a.qxd 16/12/2005 11:02 Page 181

so the new price is

43 000 × 0.75 = $32 250

(b) The scale factor is

1 −=0.85

so the original price was

39.95 ÷ 0.85 = $47

==0.92

which can be thought of as

1 −

so the fall is 8%.

100

174 989

190 205

new value

old value

100

Mathematics of Finance

182

Practice Problem

(a) Current monthly output from a factory is 25 000. In a recession, this is expected to fall by 65%.

Estimate the new level of output.

(b) As a result of a modernization programme, a firm is able to reduce the size of its workforce by

24%. If it now employs 570 workers, how many people did it employ before restructuring?

The ﬁnal application of scale factors that we consider is to the calculation of overall

percentage changes. It is often the case that over various periods of time the price of a good is

subject to several individual percentage changes. It is useful to be able to replace these by an

equivalent single percentage change spanning the entire period. This can be done by simply

multiplying together successive scale factors.

Example

(a) Share prices rise by 32% during the ﬁrst half of the year and rise by a further 10% during the second

half. What is the overall percentage change?

(b) Find the overall percentage change in the price of a good if it rises by 5% in a year but is then reduced

by 30% in a sale.

MFE_C03a.qxd 16/12/2005 11:02 Page 182

Solution

(a) To ﬁnd the value of shares at the end of the ﬁrst 6 months we would multiply by

1 +=1.32

and at the end of the year we would multiply again by the scale factor

1 +=1.1

The net effect is to multiply by their product

1.32 × 1.1 = 1.452

which can be thought of as

1 +

so the overall change is 45.2%.

Notice that this is not the same as

32% + 10% = 42%

This is because during the second half of the year we not only get a 10% rise in the original value, but

we also get a 10% rise on the gain accrued during the ﬁrst 6 months.

(b) The individual scale factors are 1.05 and 0.7, so the overall scale factor is

1.05 × 0.7 = 0.735

The fact that this is less than 1 indicates that the overall change is a decrease. Writing

0.735 = 1 − 0.265 = 1 −

we see that this scale factor represents a 26.5% decrease.

26.5

100

45.2

100

3.1 • Percentages

183

Practice Problem

5 Find the single percentage increase or decrease equivalent to

(a) an increase of 30% followed by an increase of 40%

(b) a decrease of 30% followed by a decrease of 40%

We conclude this section by describing two applications of percentages in macroeconomics:

 index numbers

 inﬂation.

We consider each of these in turn.

MFE_C03a.qxd 16/12/2005 11:02 Page 183

3.1.1 Index numbers

Economic data often take the form of a time series; values of economic indicators are available

on an annual, quarterly or monthly basis, and we are interested in analysing the rise and fall of

these numbers over time. Index numbers enable us to identify trends and relationships in the data.

The following example shows you how to calculate index numbers and how to interpret them.

Mathematics of Finance

184

Example

Table 3.1 shows the values of household spending (in billions of dollars) during a 5-year period. Calculate

the index numbers when 2000 is taken as the base year and give a brief interpretation.

Solution

When ﬁnding index numbers, a base year is chosen and the value of 100 is allocated to that year. In this

example, we are told to take 2000 as the base year, so the index number of 2000 is 100. To ﬁnd the index

number of the year 2001 we work out the scale factor associated with the change in household spending

from the base year, 2000 to 2001, and then multiply the answer by 100.

In this case, we get

× 100 = 103.8

This shows that the value of household spending in 2001 was 103.8% of its value in 2000. In other words,

household spending increased by 3.8% during 2001.

For the year 2002, the value of household spending was 716.6, giving an index number

× 100 = 102.8

This shows that the value of household spending in 2002 was 102.8% of its value in 2000. In other words,

household spending increased by 2.8% between 2000 and 2002. Notice that this is less than that calculated

for 2001, reﬂecting the fact that spending actually fell slightly during 2002. The remaining two index num-

bers are calculated in a similar way and are shown in Table 3.2.

716.6

697.2

723.7

697.2

index number = scale factor from base year × 100

Table 3.1

Year

1999 2000 2001 2002 2003

Household spending 686.9 697.2 723.7 716.6 734.5

Table 3.2

Year

1999 2000 2001 2002 2003

Household spending 686.9 697.2 723.7 716.6 734.5

Index number 98.5 100 103.8 102.8 105.3

MFE_C03a.qxd 16/12/2005 11:02 Page 184

Index numbers themselves have no units. They merely express the value of some quantity as

a percentage of a base number. This is particularly useful, since it enables us to compare how

values of quantities, of varying magnitudes, change in relation to each other. The following

example shows the rise and fall of two share prices during an 8-month period. The prices (in

dollars) listed for each share are taken on the last day of each month. Share A is exceptionally

cheap. Investors often include this type of share in their portfolio, since they can occasionally

make spectacular gains. This was the case with many dot.com shares at the end of the 1990s.

The second share is more expensive and corresponds to a larger, more established ﬁrm.

3.1 • Percentages

185

Practice Problem

6 Calculate the index numbers for the data shown in Table 3.1, this time taking 1999 as the base year.

Example

Find the index numbers of each share price shown in Table 3.3, taking April as the base month. Hence

compare the performances of these two share prices during this period.

Table 3.3

Month Jan Feb Mar Apr May Jun Jul Aug

Share A 0.31 0.28 0.31 0.34 0.40 0.39 0.45 0.52

Share B 6.34 6.40 6.45 6.52 6.57 6.43 6.65 7.00

Table 3.4

Month Jan Feb Mar Apr May Jun Jul Aug

Index of share price A (April

100) 91.2 82.3 91.2 100 117.6 114.7 132.4 152.9

Index of share price B (April

100) 97.2 98.2 98.9 100 100.8 98.6 102.0 107.4

Solution

The index numbers have been listed in Table 3.4. Notice that both shares are given the same index number

of 100 in April, which is the base month. This is despite the fact that the values of the two shares are very

different. This creates ‘a level playing-ﬁeld’, enabling us to monitor the relative performance of the two

shares. The index numbers show quite clearly that share A has outperformed share B during this period.

Indeed, if an investor had spent $1000 on shares of type A in January, they could have bought 3225 of them,

which would be worth $1677 in August, making a proﬁt of $677. The corresponding proﬁt for share B is

only $99.

MFE_C03a.qxd 16/12/2005 11:02 Page 185

The table shows that the base quarter is the ﬁrst quarter of 2005 because the index number is

100 in 05Q1. It is, of course, easy to ﬁnd the percentage change from this quarter to any sub-

sequent quarter. For example, the index number associated with the third quarter of 2005 is

110.2, so we know immediately that the percentage change in output from 05Q1 to 05Q3 is

10.2%. However, it is not immediately obvious what the percentage change is from, say, 04Q2

to 05Q2. To work this out, notice that the index number has increased by

106.3 − 98.1 = 8.2

so the percentage increase is

× 100 = 8.4%

Alternatively, note that the scale factor of this change is

= 1.084

which corresponds to an 8.4% increase.

Similarly, the scale factor of the change from 04Q3 to 05Q1 is

= 0.952

This is less than 1, reﬂecting the fact that output has fallen. To ﬁnd the percentage change we

write the scale factor as

1 − 0.048

which shows that the percentage decrease is 4.8%.

100

105

106.3

98.1

8.2

98.1

Mathematics of Finance

186

Incidentally, if the only information you have about the time series is the set of index

numbers, then it is possible to work out the percentage changes between any pair of values.

Table 3.5 shows the index numbers of the output of a particular ﬁrm for the years 2004

and 2005.

Table 3.5

Output

04Q1 04Q2 04Q3 04Q4 05Q1 05Q2 05Q3 05Q4

Index 89.3 98.1 105.0 99.3 100 106.3 110.2 105.7

Practice Problem

7 Use the index numbers listed in Table 3.5 to find the percentage change in output from

(a) 05Q1 to 05Q4

(b) 04Q1 to 05Q4

MFE_C03a.qxd 16/12/2005 11:02 Page 186

3.1 • Percentages

187

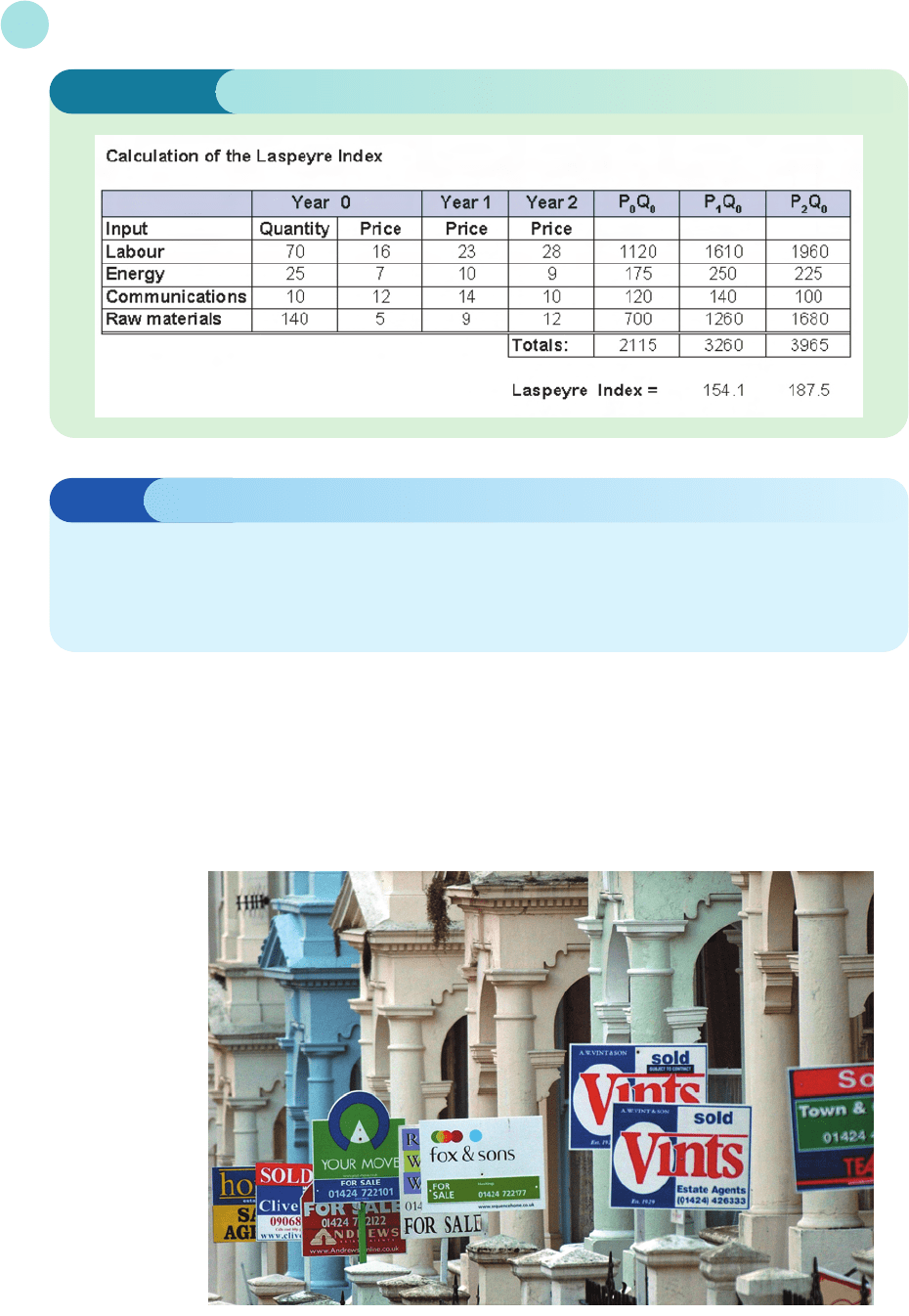
Example

Table 3.6 shows the unit costs of labour, energy, communications and raw materials during a 3-year

period. In year 0, a ﬁrm used 70 units of labour, 25 units of energy, 10 units of communication and 140

units of raw materials. Taking year 0 as the base year, calculate an appropriate index number for years 1

and 2.

EXCEL

Table 3.6

Year 0 Year 1 Year 2

Labour 16 23 28

Energy 710 9

Communications 12 14 10

Raw materials 5912

Solution

We are told to take year 0 as the base year, so the index number for year 0 is 100. One way of calculating

the index number for subsequent years would be to work out the totals of each column in Table 3.6

and ﬁnd the associated scale factors of these. On this basis, the index number for year 1 would be cal-

culated as

× 100 = 140

However, this fails to take into account the fact, for example, that we use twice as many units of raw

materals than labour. It is important that each item is weighted according to how many units of each type

are used. To do this, all we have to do is to multiply each of the unit costs by the associated quantities. The

appropriate index number is then worked out as

× 100 = 154.1

The fact that this number is greater than before is to be expected because the unit price of raw materials has

nearly doubled, and the ﬁrm uses a greater proportion of these in its total costs. Index numbers that are

weighted according to the quantity consumed in the base year are called Laspeyre indices. Spreadsheets

provide an easy way of presenting the calculations. For each year, we simply include an extra column in the

table, for the products P

where Q

denotes the quantities used in the base year, and P

denotes the unit

prices in year n. The Laspeyre index for year n is then worked out as

× 100

Figure 3.1 (overleaf) shows the completed spreadsheet. The Laspeyre indices for years 1 and 2 are seen to

be 154.1 and 187.5, respectively. Notice that this index has increased rapidly over this period, in spite of the

fact that communication and energy costs have hardly changed. This is because expenditure is dominated

by labour and raw material costs, which have both increased substantially during this time.

total of column P

23 × 70 + 10 × 25 + 14 × 10 + 9 × 140

16 × 70 + 7 × 25 + 12 × 10 + 5 × 140

23 + 10 + 14 + 9

16 + 7 + 12 + 5

MFE_C03a.qxd 16/12/2005 11:02 Page 187

3.1.2 Inﬂation

Over a period of time, the prices of many goods and services usually increase. The annual rate

of inﬂation is the average percentage change in a given selection of these goods and services,

over the previous year. Seasonal variations are taken into account, and the particular basket

of goods and services is changed periodically to reﬂect changing patterns of household

Mathematics of Finance

188

Advice

There are other methods for assessing the variation of a ‘basket’ of values over time. Index

numbers that are weighted according to the quantity consumed in the current year

(instead of the base year) are called

Paasche indices. An example of this is given in Practice

Problem 22 at the end of this section.

Figure 3.1

MFE_C03a.qxd 16/12/2005 11:02 Page 188

Solution

The raw ﬁgures shown in Table 3.7 give the impression that houses increased steadily in value throughout

this period, with a quite substantial gain during the ﬁrst year. However, if inﬂation had been very high then

the gain in real terms would have been quite small. Indeed, if the rate of inﬂation were to exceed the per-

centage rise of this nominal data, then the price of a house would actually fall in real terms. To analyse this

situation we will use Table 3.8, which shows the rates of inﬂation during this period. Notice that since the

house prices listed in Table 3.8 are quoted at the end of each year, we are not interested in the rate of

inﬂation during 1990.

We are told in the question to choose 1991 as the base year and calculate the value of the house at ‘1991

prices’. The value of the house at the end of 1991 is obviously $89 000, since no adjustment need be made.

At the end of 1992, the house is worth $93 000. However, during that year inﬂation was 7.1%. To adjust this

price to ‘1991 prices’ we simply divide by the scale factor 1.071, since we are going backwards in time. We get

= 86 835

93 000

1.071

3.1 • Percentages

189

Example

Table 3.7 shows the price (in thousands of dollars) of an average house in a certain town during a 5-year

period. The price quoted is the value of the house at the end of each year. Use the annual rates of inﬂation

given in Table 3.8 to adjust the prices to those prevailing at the end of 1991. Compare the rise in both the

nominal and real values of house prices during this period.



Table 3.7

Year

1990 1991 1992 1993 1994

Average house price 72 89 93 100 106

Table 3.8

Year

1991 1992 1993 1994

Annual rate of inﬂation 10.7% 7.1% 3.5% 2.3%

expenditure. The presence of inﬂation is particularly irritating when trying to interpret a time

series that involves a monetary value. It is inevitable that this will be inﬂuenced by inﬂation

during any year, and what is of interest is the ﬂuctuation of a time series ‘over and above’ inﬂation.

Economists deal with this by distinguishing between nominal and real data. Nominal data are

the original, raw data such as those listed in tables in the previous sub-section. These are based

on the prices that prevailed at the time. Real data are the values that have been adjusted to take

inﬂation into account. The standard way of doing this is to pick a year and then convert the

values for all other years to the level that they would have had in this base year. This may sound

rather complicated, but the idea and calculations involved are really quite simple as the fol-

lowing example demonstrates.

MFE_C03a.qxd 16/12/2005 11:02 Page 189