Иванов-Смоленский А.В. Электрические машины т 2

Подождите немного. Документ загружается.

490

чае потокосцепление сверхпроводящей обмотки возбуждении от бы-

стрых составляющих токов должно быть равно нулю, поскольку до

начала процесса эти токи отсутствовали:

= L

f 2

+ L

к d 2

= Ψ

f 0

= 0.

Поэтому быстрые составляющие токов должны находиться в соот-

ношении

f 2

= – L

к d 2

/ L

. (72.13)

Подставляя в (72.11) уравнение (72.13), получаем для индуктивно-

сти демпферной обмотки при короткозамкнутой обмотке возбужде-

ния выражение, совпадающее с ранее полученным:

. (72.14)

Индуктивность по (72.14) соответствует картине поля рис. 72.4. В

этом легко убедиться, вспомнив, что индуктивности пропорциональ-

ны магнитным проводимостям немагнитных промежутков, через ко-

торые замыкаются определяющие их магнитные поля. Как вытекает

из (71.21), (71.22), (71.43),

;; ,

где Λ

— проводимость зазора для продольного потокосцепления

по рис. 72.2 или 72.3; Λ

f σ

— проводимость промежутков между по-

люсами для потокосцепления рассеяния обмотки возбуждения Ψ

fσ

по рис. 72.2; Λ

к d σ

— проводимость немагнитных промежутков для

потокосцепления рассеяния продольной демпферной обмотки Ψ

кdσ

по рис. 72.3.

Таким же образом индуктивность L можно записать через соответ-

ствующую проводимость: L = . Выразив индуктивности в (72.14)

через проводимости, найдем:

где

А это означает, что проводимость Λ для полного потокосцепления

складывается из параллельно включенных проводимостей Λ

кdσ

, через которые замыкаются потокосцепления Ψ

кdσ

и (см.

кd

кd2

----------

кdσ

---------

f σ

---------

⎝⎠

⎛⎞

1–

+σL

кd

== =

= L

f σ

= L

кdσ

ΛΛ

кdσ

′

---------

f σ

----------

кdσ

-------------

′

491

рис. 72.4), а представляет собой проводимость двух последова-

тельно включенных немагнитных промежутков: зазора с проводимо-

стью Λ

и промежутков между полюсами с проводимостью Λ

f σ

Именно через эти последовательно включенные проводимости замы-

кается поле, образующее потокосцепление (см. рис. 72.4). Про-

никновению поля внутрь контура возбуждения препятствует ток

f 2

[см. (72.13)], индуктированный в обмотке возбуждения (потокос-

цепление контура возбуждения должно остаться равным нулю и, сле-

довательно, линии поля, сцепленные с контуром, должны отсутство-

вать!). Поэтому полю приходится замыкаться через проводи-

мость Λ

f σ

, т.е. по тому же пути, по которому замыкается потокосцеп-

ление рассеяния возбуждения Ψ

f σ

(на рис. 72.4 показана пунктиром

линия поля, соответствующая полю рассеяния обмотки возбужде-

ния).

Найдем теперь наибольшие (начальные) значения быстрых (i

а2

кd2

) и медленных (i

а1

, i

кd1

) составляющих свободных токов в (72.6).

Одно из уравнений, необходимых для определения этих токов, а

именно (72.13), получено выше. Считая заданным начальный i

f н

установившийся i

f у

токи в обмотке возбуждения, выразим начальный

ток

f н

= i

f (t = 0)

= i

f у

+ i

f c(t = 0)

= i

f у

+ i

f 1

+ i

f 2

. (72.15)

Имея в виду, что начальный ток в демпферной обмотке при t = 0

отсутствует, получаем

к d(t = 0)

= i

к d 1

+ i

к d 2

= 0. (72.16)

Четвертое уравнение для определения произвольных токов полу-

чаем, применяя уравнение контура демпферной обмотки (72.5) для

интервала времени, когда быстрые составляющие токов успели затух-

нуть, т.е. = 0. Подставляя (72.6) в (72.5) и сокращая на общий

множитель , находим

. (72.17)

Решая уравнения (72.13), (72.17) совместно, получаем

;;

′

– t / T

кd

кd1

------

кd

кd1

f 1

+()–0=

f 1

f н

f у

–()

кd

–

----------------------

= i

f 2

f н

f у

–()

кd

–

----------------------

492

. (72.18)

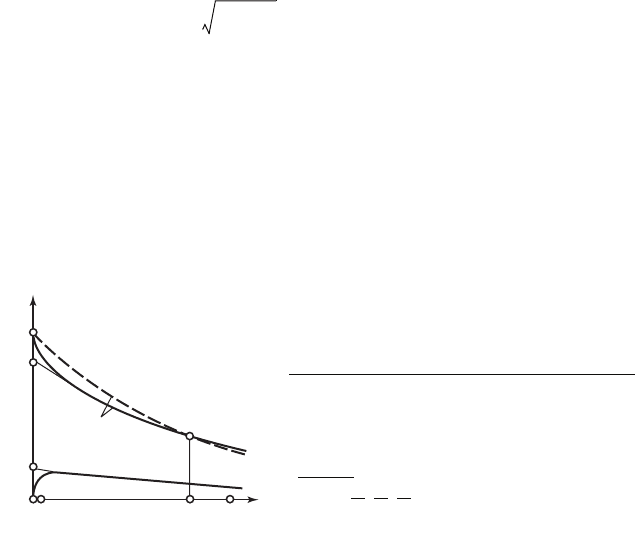
Кривые изменения токов i

и i

кd

в переходном процессе, построен-

ные по (72.6), (72.18) для случая гашения поля (i

f у

= 0), показаны на

рис. 72.5 (сплошные линии). Кривые построены при T

= 0,8T

; T

кd

= 0,2T

; L

кd

= 1,1; L

= 1,14; σ = 0,2; T

= 0,04T

. На том же ри-

сунке приведена кривая тока i

(штриховая линия) в случае гашения

поля при разомкнутой демпферной обмотке, когда i

кd

= 0, и затухание

происходит с постоянной времени T

= T

– T

кd

. Видно, что в начале

процесса (при t < T

) быстрее затухает ток возбуждения в случае ко-

роткозамкнутой демпферной обмотки, однако при t = T

сплошная и

штриховая линии пересекаются, и в дальнейшем (при t > T

) быстрее

затухает ток возбуждения в случае разомкнутой демпферной обмотки

(так как T

< T

= T

+ T

кd

). Таким образом, в конечном счете присут-

ствие демпферной обмотки затягивает переходный процесс. Пред-

ставляет интерес выяснить, как влияет демпферная обмотка на зату-

хание напряжения обмотки статора при гашении поля. Напряжение

обмотки статора , где u

и u

рассчитываются по (71.44).

При разомкнутой обмотке статора i

= i

кd

= 0, соответственно

= i

+ i

кd

= 0 и отличается от нуля только продольное потокос-

цепление

, (72.19)

где

;;

кd1

– i

кd2

f н

f у

–()

кd

–()

---------------------------------

кd

+()Ψ

– t / T

+==

f н

кd

–

-----------------------------

=Ψ

f н

кd

–

-----------------------------

кd

---------

–=

f н

f 1

d

d1

Рис. 72.5. Изменение тока возбуждения i

тока демпферной обмотки i

кd

в процессе га-

шения поля:

— при замкнутой демпферной об-

мотке; — при разомкнутой демп-

ферной обмотке

493

Поскольку

;

нетрудно убедиться в том, что при промышленной частоте f = 50 Гц,

когда ω = 2π f = 314 рад/с, и при встречающихся в синхронных маши-

нах постоянных времени T

≈ 1—12 с, T

≈ (0,02— 0,06)T

напряжение

, совпадающее с ЭДС вращения, во много раз больше, чем напряже-

ние u

, совпадающее с трансформаторной ЭДС, u

>> u

. Поэтому

напряжение обмотки статора U = u

= ωΨ

пропорционально продоль-

ному потокосцеплению Ψ

и изменяется при гашении поля таким же

образом, как это потокосцепление.

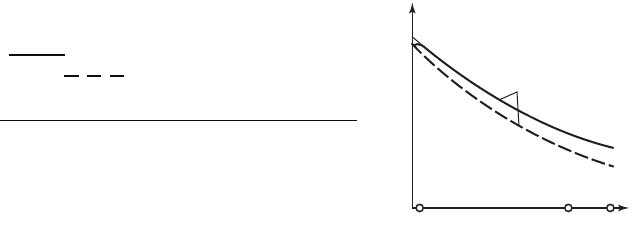
Кривая изменения потокосцепления Ψ

, построенная по (72.19)

при тех же условиях, что и на рис 72.5, приведена на рис. 72.6 (сплош-

ная линия). Как видно, Ψ

содержит очень маленькую быструю со-

ставляющую и большую медленную составляющую

. Там же штриховой линией показано потокосцепление Ψ

= при разомкнутой демпферной обмотке, которое на всех

этапах процесса затухает быстрее, чем при замкнутой демпферной

обмотке. Таким образом, влияние демпферной обмотки проявляется

в замедлении процесса гашения поля. Другие переходные процессы,

связанные с изменением возбуждения, в присутствии демпферной

обмотки также замедляются.

72.4. Переходные процессы в машине без демпферной

обмоти при оротозамнтой обмоте статора

В этом случае ток, индуктированный в короткозамкнутой обмотке

статора, оказывает существенное влияние на магнитное поле и пото-

косцепление обмотки возбуждения. Поэтому при анализе переходно-

ωΨ

– t / T

ωΨ

– t / T

dΨ

--------

–

----------

– t / T

----------

– t / T

–==

– t / T

dн

– t / T

;

dн

;

Рис. 72.6. Изменение потокосцепления обмот-

ки статора Ψ

в процессе гашения поля:

— при замкнутой демпферной об-

мотке; — при разомкнутой демп-

ферной обмотке

494

го процесса должны быть совместно рассмотрены: уравнение для об-

мотки возбуждения (71.26)

+ pΨ

= u

, (72.20)

где Ψ

= L

+ L

, и уравнения для короткозамкнутых контуров

статора по продольной и поперечной осям (70.44), записанные при

= u

= 0:

+ pΨ

– ωΨ

= 0; (71.21)

+ pΨ

+ ωΨ

= 0. (72.22)

Поскольку << , приходим к выводу, что Ψ

= L

= 0

и Ψ

= L

+ L

. Следовательно, в обмотке статора, как и в устано-

вившемся режиме короткого замыкания (см. гл. 61), имеется только

продольный ток i

= –L

, а поперечный ток отсутствует (i

= 0).

Вводя ток i

в выражение для потокосцепления Ψ

, увидим, как влия-

ет короткозамкнутая обмотка статора на индуктивность обмотки воз-

буждения

где

. (72.23)

За счет размагничивающего действия поля от тока i

потокосцеп-

ление обмотки возбуждения уменьшается. При этом оно выражается

через — индуктивность обмотки возбуждения при короткозамкну-

той обмотке статора, которая всегда меньше, чем индуктивность об-

мотки возбуждения L

при разомкнутых других обмотках, т.е.

<< L

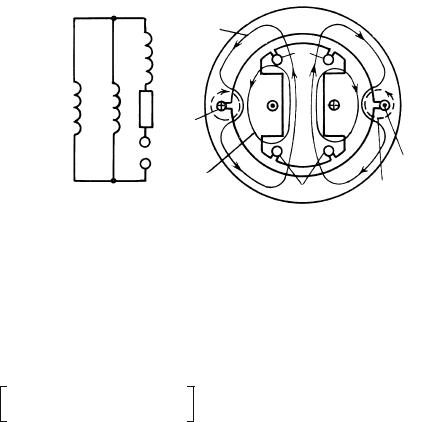
. Картина поля возбуждения при короткозамкнутой обмотке

статора и электрическая схема замещения, обладающая индуктивно-

стью и постоянной времени , показаны на рис. 72.7.

Нетрудно убедиться в том, что схема замещения рис. 72.7 представля-

ет собой частный случай общей схемы по рис. 71.9 при разомкнутой

демпферной обмотке и короткозамкнутой обмотке статора. Из карти-

ны поля видно, что потокосцепление обмотки возбуждения склады-

вается из потокосцепления рассеяния Ψ

f σ

, пропорционального про-

ωΨ

+ L

---------

–

⎝⎠

⎜⎟

⎛⎞

′

===

′

------

---------

– L

f σ

---------

------

⎝⎠

⎛⎞

1–

+== =

′

/ R

495

водимости Λ

f σ

, и из пото-

косцепления , пропор-

ционального проводимости

, причем представ-

ляет собой проводимость

двух последовательно вклю-

ченных немагнитных про-

межутков: зазора с проводи-

мостью Λ

и промежутков,

через которые замыкаются

поля рассеяния обмотки ста-

тора, с проводимостью Λ

Поэтому индуктивность обмотки возбуждения при короткозамкнутой

обмотке статора

что совпадает с ранее полученным выражением (72.23). После выра-

жения потокосцепления Ψ

в (72.20) через индуктивность и ток

возбуждения i

, (72.24)

получим дифференциальное уравнение, отличающееся от (72.1) толь-

ко тем, что в него входит вместо L

индуктивность . Поэтому реше-

ние уравнения можно не повторять, а воспользоваться результатами

анализа переходного процесса при изменении напряжения возбужде-

ния в случае, когда другие обмотки разомкнуты (см. § 72.2), вводя в

полученное решение вместо L

. Уравнение для тока возбуждения

получим из (72.2)

, (72.25)

где — постоянная времени обмотки возбуждения при ко-

роткозамкнутой обмотке статора.

Поскольку < T

, переходные процессы при гашении поля и при

изменении возбуждения протекают быстрее при короткозамкнутой

обмотке статора.

′

------

′

f σ

---------

-------

⎝⎠

⎛⎞

1–

+ L

f σ

---------

------

⎝⎠

⎛⎞

1–

+== = =

′

+ u

′

f у

f н

f у

–()e

– tT

′

⁄

′

⁄=

′

;

²d

;

Рис. 72.7. Схема замещения и картина поля

для определения индуктивности обмотки

возбуждения при короткозамкнутой обмотке

статора

′

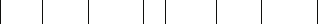
496

72.5. Переходные процессы в машине с демпферной

обмотой при оротозамнтой обмоте статора

В этом случае требуется рассмотреть совместно: уравнения для

обмотки возбуждения (71.26)

+ pΨ

= u

, (72.26)

для демпферной обмотки

к d

+ pΨ

к d

= 0 (72.27)

и уравнения для короткозамкнутой обмотки статора (71.44), записан-

ные при u

= u

= 0,

+ pΨ

– ωΨ

= 0; (72.28)

+ pΨ

+ ωΨ

= 0. (72.29)

Поскольку << , << , из (72.28) следует,

что Ψ

= L

+ L

кq

= 0 и, следовательно, i

= i

кq

= 0. Тогда из (72.29)

получаем

= L

+ L

+ i

к d

) = 0,

откуда

Выражая ток i

в потокосцеплении Ψ

(72.26) через токи i

и i

кd

находим

, (72.30)

где — индуктивность обмотки возбуждения при короткозамкну-

той обмотке статора по (72.23); — взаимная ин-

дуктивность между обмоткой возбуждения и демпферной обмоткой

при короткозамкнутой обмотке статора.

Из рис. 72.7 видно, что эта взаимная индуктивность определяется

по потокосцеплению с демпферной обмоткой при короткозамк-

нутой обмотке статора, поэтому

. (72.31)

ωΨ

pΨ

ωΨ

–

кd

+()

--------------------------------

кd

++ L

′

кd

+==

′

---------

------

⎝⎠

⎛⎞

1–

′

----------

′

---------

-------

⎝⎠

⎛⎞

1–

---------

------

⎝⎠

⎛⎞

1–

== = =

497

Аналогично, выражая ток i

в потокосцеплении Ψ

кd

(72.27) через

токи i

и i

кd

, находим:

, (72.32)

где

(72.33)

— индуктивность демпферной обмотки по продольной оси при ко-

роткозамкнутой обмотке статора и разомкнутой обмотке возбужде-

ния (рис. 72.8).

Вводя потокосцепления Ψ

и Ψ

кd

, выраженные через токи i

и i

кd

в (72.26), (72.27), (72.4), получаем систему дифференциальных урав-

нений, отличающуюся от системы (72.4), составленной для случая

разомкнутой обмотки статора, только тем, что в нее входят индуктив-

ности , и соответственно вместо индуктивностей L

, L

кd

. Поскольку индуктивности при короткозамкнутой обмотке стато-

ра имеют тот же порядок, что и при разомкнутой обмотке, на систему

уравнений (72.26), (72.27) могут быть распространены все допуще-

ния, принятые выше при решении системы (72.4). При этом вместо

повторного решения системы (72.26), (72.27) можно воспользоваться

результатами решения системы (72.4), вводя во все формулы изме-

ненные значения индуктивностей. Тогда в формулы войдут следую-

щие новые параметры:

постоянная времени обмотки возбуждения при короткозамкнутой

обмотке статора

; (72.34)

постоянная времени демпферной обмотки по продольной оси при

короткозамкнутой обмотке статора

;(72.35)

кd

++ L

кd

′

кd

′

+==

кd

′

кdσ

---------

------

⎝⎠

⎛⎞

1–

′

кd

′

/ R

кd

′

кd

′

/ R

кd

²dU

;

²dU

²d

²d ²d

;

Рис. 72.8. Схема замещения и

картина поля для определения

индуктивности демпферной

обмотки по продольной оси

при короткозамкнутой обмот-

ке статора

кd

′

498

коэффициент рассеяния обмоток возбуждения и демпферной при

короткозамкнутой обмотке статора

; (72.36)

постоянные времени медленного и быстрого процессов [по анало-

гии с (72.10)]

; ; (72.37)

наибольшие значения медленной и быстрой составляющих тока

возбуждения

; ; (72.38)

наибольшие значения медленной и быстрой составляющих тока

демпферной обмотки

; (72.39)

уравнения для токов в обмотке возбуждения и в демпферной об-

мотке при короткозамкнутой обмотке статора [по аналогии с (72.6)]

; . (72.40)

Поскольку < T

, < T

, переходные процессы при изменении

возбуждения при короткозамкнутой обмотке статора протекают бы-

стрее, чем при разомкнутой.

σ′ 1

′

()

′

кd

′

-----------------

–=

′

кd

′

+= T

′

σ′T

кd

′

f 1

′

f н

f у

–()

′

кd

′

–

′

–

----------------------

= i

f 2

′

f н

f у

–()

кd

′

–

′

–

----------------------

кd1

′

– i

кd2

′

f н

f у

–()

′

кd

′

кd

′

–()

----------------------------------

f у

f 1

′

– t / T

′

f 2

′

– t / T

′

++= i

кd

кd1

′

– t / T

′

кd2

′

– t / T

′

499

Глава семьдесят третья

ПЕРЕХОДНЫЙ ПРОЦЕСС ПРИ СИММЕТРИЧНОМ

КОРОТКОМ ЗАМЫКАНИИ ОБМОТКИ СТАТОРА

СИНХРОННОЙ МАШИНЫ

73.1. Общая харатеристиа переходноо процесса.

Начальные и онечные словия

Переходный процесс при симметричном коротком замыкании об-

мотки статора может рассматриваться как частный случай переходно-

го процесса, вызванного внезапным уменьшением или увеличением

напряжения сети U

, параллельно с которой работает синхронная ма-

шина.

Предположим, что при t < 0 (до начала переходного процесса)

машина работала в установившемся режиме параллельно с сетью.

Начальный режим (см. § 71.8) характеризуется током возбуждения i

f н

и составляющими потокосцеплений статора

d н

= i

d н

+ i

f н

и Ψ

q н

= i

q н

которым соответствуют токи

и , (73.1)

где E

f н

= ωL

f н

— начальная ЭДС возбуждения.

Из (71.44)

(73.2)

где e

dн

= ωΨ

qн

; e

qн

= –ωΨ

dн

— составляющие собственной ЭДС ма-

шины E

в начальном режиме.

Пренебрегая малыми членами Ri

dн

и Ri

qн

и имея в виду, что pΨ

dн

= pΨ

qн

= 0, найдем суммарную ЭДС в продольном и поперечном кон-

турах

d н

+ e

d н

= 0, u

q н

+ e

q н

= 0. (73.3)

qн

----------

= i

dн

f н

/ ω–

-----------------------------------

dн

pΨ

dн

–+ u

dн

qн

pΨ

qн

–+ u

qн

⎭

⎬

⎫