Иванов-Смоленский А.В. Электрические машины т 2

Подождите немного. Документ загружается.

470

Приведенные активные сопротивления и индуктивности рассея-

ния роторных контуров определяются как произведение неприведен-

ной величины на коэффициент приведения по (71.6), причем индекс

приведения у приведенных параметров часто опускается.

Активное сопротивление приведенной обмотки возбуждения

, (71.18)

где ρ

— удельное электрическое сопротивление обмотки; l

— сред-

няя длина полувитка обмотки; S

— сечение провода обмотки.

Активное сопротивление приведенной демпферной обмотки по

продольной оси

, (71.19)

где ρ

— удельное электрическое сопротивление стержней обмотки;

— длина стержня; S

— сечение стержня; n

— число стержней на

один полюс; — коэффициент распределения демпфер-

ной обмотки; α

= ( — расстояние между соседними

стержнями); c

кd

= 1,05—1,1 — коэффициент, учитывающий влияние

короткозамыкающих элементов.

Активное сопротивление приведенной демпферной обмотки по

поперечной оси

к q

= k

к d

, (71.20)

где k

= 0,75 для демпферной обмотки с полными короткозамыкаю-

щими кольцами; k

≈ 10 для демпферной обмотки, в которой отсут-

ствуют электрические соединения между короткозамыкающими сег-

ментами соседних полюсов.

Индуктивное сопротивление рассеяния приведенной обмотки воз-

буждения

, (71.21)

где λ

fσ

— коэффициент проводимости для потокосцепления рассея-

ния обмотки возбуждения (на единицу расчетной длины машины, на

один полюс).

------------

о1

---------------------

⎝⎠

⎛⎞

------------

кd

-----

о1

---------------------

⎝⎠

⎛⎞

кd

1 k

о.к

–()n

------------------------------------

о.к

sin

----------------------

πt

/ τ t

fσ

------------

о1

---------------------

⎝⎠

⎛⎞

f σ

471

Индуктивное сопротивление рассеяния приведенной демпферной

обмотки по продольной оси

, (71.22)

где λ

кdσ

— коэффициент проводимости для потокосцепления рассея-

ния демпферной обмотки по продольной оси (на единицу расчетной

длины, на один полюс).

Индуктивное сопротивление рассеяния приведенной демпферной

обмотки по поперечной оси

к q σ

= k

к d σ

, (71.23)

где k

= 0,75 для полной демпферной обмотки с короткозамыкающи-

ми кольцами; k

= 4 для демпферной обмотки, в которой отсутствуют

электрические соединения между короткозамыкающими сегментами

соседних полюсов.

Коэффициенты проводимости λ

f σ

, λ

кdσ

зависят от формы про-

странства между магнитопроводами, в котором размещаются прово-

да обмоток, и от размещения проводников в этом пространстве. Фор-

мулы для расчета этих проводимостей имеются в [26].

71.5. Запись равнений напряжений онтров через фазные

величины

Поступив так же, как для асинхронной машины (см. гл. 69), выде-

лим предварительно из всех фазных величин статора (токов i

AΣ

, i

BΣ

CΣ

) составляющие, в которых не содержатся величины нулевой по-

следовательности (i

, Ψ

, u

), т.е. составляющие, рассчитанные по

формулам:

(71.24)

где

= (i

A Σ

+ i

B Σ

+ i

C Σ

)/3; Ψ

= (Ψ

A Σ

+ Ψ

B Σ

+ Ψ

C Σ

)/3.

В проведении аналогичной операции для приведенных роторных

величин нет нужды, так как система токов в приведенных трехфазных

роторных контурах не содержит токов нулевой последовательности.

кdσ

------------

о1

---------------------

⎝⎠

⎛⎞

кdσ

AΣ

–= ; i

BΣ

–= ;

AΣ

–= ; Ψ

BΣ

–= ,

⎭

⎬

⎫

472

Как видно из рис. 71.5, сумма этих токов, распространенная на все три

фазы, всегда равна нулю. Например:

После выделения из фазных величин составляющих нулевой по-

следовательности уравнения напряжений синхронной машины рас-

падаются на две системы уравнений: систему уравнений напряжений

для фазных величин, не содержащих составляющих нулевой после-

довательности, и уравнение напряжений для фазных величин нуле-

вой последовательности.

Уравнения напряжений для фазных величин, не содержащих со-

ставляющих нулевой последовательности, записываются для всех

фаз статора (для фаз A, В, С ):

(71.25)

и для главных фаз приведенных трехфазных контуров ротора, пока-

занных на рис. 71.5,

(71.26)

Уравнение напряжений для величин нулевой последовательности

записывается для одной из фаз статора

. (71.27)

Заметим, что в (71.25), (71.26) и в других уравнениях, записанных

через приведенные величины роторных контуров, индекс приведения

опущен. Сделано это для облегчения использования уравнений при

анализе переходных процессов.

′

– 0,5i

′

()–0,5i

′

()++ 0=

dΨ

-----------

;+=

dΨ

-----------

;+=

dΨ

-----------

⎭

⎪

⎬

⎪

⎫

dΨ

---------

;+=

кd

dΨ

кd

--------------

;+=

кq

dΨ

кq

--------------

.+=

⎭

⎪

⎬

⎪

⎫

dΨ

-----------

473

Потокосцепления в (71.25), (71.27) выражаются через токи фаз

статора, токи в главных фазах ротора и соответствующие индуктив-

ности (см. выше). Например, потокосцепление фазы А статора

= L

AAΣ

+ L

ABΣ

+ L

ACΣ

+ L

A к d

к d

+ L

A к q

к q

; (71.28)

потокосцепление главной фазы приведенной обмотки возбуждения

= L

+ L

f к d

к d

; (71.29)

потокосцепление главной фазы приведенной демпферной обмотки по

продольной оси

к d

= L

к dA

+ L

к dB

+ L

к dC

+ L

к df

+ L

к d

; (71.30)

потокосцепление главной фазы приведенной демпферной обмотки по

поперечной оси

к q

= L

к qA

+ L

к qB

+ L

к qC

+ L

к q

; (71.31)

потокосцепление нулевой последовательности

= L

, (71.32)

где L

= L

AAσ

+ L

ABσ

+ L

ACσ

— индуктивность фазы статора для токов

нулевой последовательности (см. гл. 69).

Потокосцепления фаз В и С статора записываются аналогично.

Полные индуктивности L

AAΣ

, L

ABΣ

, L

ACΣ

(71.28) для фазы А и индук-

тивности L

BBΣ

, L

CCΣ

и другие в аналогичных уравнениях для фаз В и

С складываются из соответствующих главных индуктивностей (71.9),

(71.10) и индуктивностей рассеяния, смысл которых разъясняется в

гл. 69:

(71.33)

Полные индуктивности главных фаз приведенных роторных кон-

туров также включают в себя не только соответствующие главные ин-

дуктивности по (71.15), (71.16), но и индуктивности рассеяния по

(71.21), (71.23)

= L

+ L

f σ

; L

к d

= L

к dd

+ L

к d σ

; L

к q

= L

к qq

+ L

к q σ

. (71.34)

AAΣ

AAσ

+= ; L

BBΣ

BBσ

+= ; L

CCΣ

CCσ

+= ;

ABΣ

ABσ

+= ; L

ACΣ

ACσ

+= ; L

BCΣ

BCσ

+= .

⎭

⎬

⎫

474

71.6. Уравнения напряжений онтров в осях d, q

Система дифференциальных уравнений (71.25)—(71.27) исчерпы-

вающим образом описывает переходные процессы в синхронной ма-

шине, однако ее непосредственное решение по причинам, перечис-

ленным в гл. 69, затруднительно.

Для упрощения анализа система (71.25), (71.26), составленная для

фазных величин, преобразуется по аналогии с тем, как это сделано для

асинхронной машины в гл. 69. При этом вместо фазных величин

(токов, напряжений, потокосцеплений) введем новые переменные в

виде результирующих комплексных функций, выражаемых через соот-

ветствующие фазные величины. Результирующие комплексные функ-

ции наиболее удобно записать в комплексной плоскости d, q, ориенти-

рованной по осям магнитной симметрии ротора (действительную ось

комплексной плоскости совместим с осью d, мнимую — с осью q).

Наиболее просто выражаются результирующие комплексные функции

для величин роторных контуров по продольной оси, главная фаза ко-

торых ориентирована по продольной оси [см. рис. 71.5 и (69.22),

(69.23)]. Легко показать, что результирующие комплексные функции

токов продольных контуров равны приведенным токам контуров, про-

текающим по их главным фазам, и направлены по продольной оси:

(71.35)

Учитывая, что главная фаза поперечной демпферной обмотки сов-

падает с мнимой осью комплексной плоскости (см. рис. 71.5), нахо-

дим результирующую комплексную функцию тока поперечной демп-

ферной обмотки

. (71.36)

Как видно из уравнения, эта результирующая комплексная функ-

ция по модулю равна приведенному току поперечной демпферной

обмотки и направлена по поперечной оси.

Результирующие комплексные функции напряжений и потокосце-

плений роторных контуров выражаются через приведенные величи-

ны аналогичным образом:

;; ; ;

; . (71.37)

∼

---

–0,5i

()a

–

–0,5i

()a

–

++ ] i

;==

∼

кd

---

кd

– 0,5i

кd

()a

–

– 0,5i

кd

()a

–

++ ] i

кd

.==

⎭

⎪

⎬

⎪

⎫

∼

кq

j2[i

кq

– 0,5i

кq

()a

–

–0,5i

кq

()a

–

++ ]3⁄ ji

кq

∼

=Ψ

∼

= U

∼

кd

=Ψ

∼

кd

∼

кq

=Ψ

∼

кq

jΨ

кq

475

Результирующая комплексная функция, например, тока статора в

комплексной плоскости α, β, действительная ось которой совмещена

с осью фазы А, рассчитывается по (69.22)

В комплексной плоскости d, q, вращающейся вместе с ротором и

повернутой на угол α относительно комплексной плоскости α, β, токи

статора (69.28) представляются результирующим комплексом

. (71.38)

Таким же образом вычисляются результирующие комплексы на-

пряжения и потокосцепления статора

;

. (71.39)

Для преобразования системы уравнений статора (71.25) в уравне-

ние, записанное через результирующие комплексные функции в осях

α, β, достаточно умножить уравнение для u

на 2/3, уравнение для u

на 2a/3, уравнение для u

на 2a

/3 и сложить почленно правые и ле-

вые части этих уравнений. В результате получим только одно ком-

плексное уравнение в комплексной плоскости α, β

Все величины, которые входят в это уравнение, выражаются в ком-

плексной плоскости d, q с помощью (71.38), (71.39):

Учитывая при взятии производной, что угол α является функцией

времени, и сокращая все члены уравнения на е

jα

, получаем уравне-

ние напряжений статора в комплексной плоскости d, q

, (71.40)

где ω = dα/dt = p

Ω — электрическая угловая скорость ротора.

∼

αβ()

2 i

–

++()/3=

∼

αβ()

– jα

---

–

++()e

– jα

∼

αβ()

– jα

---

–

++()e

– jα

∼

αβ()

– jα

---

–

++()e

– jα

∼

αβ()

∼

αβ()

-----

[ Ψ

∼

αβ()

]+=

∼

jα

∼

jα

-----

[ Ψ

∼

jα

]+=

∼

d Ψ

∼

--------

jωΨ

∼

++=

476

Уравнения напряжений роторных контуров в преобразовании не

нуждаются и могут быть оставлены в виде системы (71.26), в которой

приведенные роторные величины одновременно являются проекция-

ми соответствующих результирующих комплексов на ось d или q [см.

(71.35), (71.36), (71.37)]. Нуждается в преобразовании лишь сумма

членов, связанных с токами фаз статора в уравнениях для потокосце-

плений роторных контуров. Покажем, например, как проводится та-

кое преобразование для потокосцепления обмотки возбуждения, об-

разованного токами статора. Это потокосцепление соответствует

первым трем членам в (71.29). Токи фаз статора в этих членах выра-

жаются как проекции результирующей комплексной функции тока

(71.38) на направления осей фаз (для фазы А — на направление

относительно комплексной плоскости d, q; для фазы В — на

направление ; для фазы С — на направление ):

;

Взаимные индуктивности L

, L

с учетом (71.11), (71.14) вы-

ражаются через косинусы углов α, α + 4π/3 и α + 2π/3, которые в

свою очередь представляются в комплексной форме:

;

После указанных подстановок и необходимых преобразований

найдем:

где L

= 3L

/2 — главная индуктивность якоря по продольной оси.

Заметив, что — проекция результирующего комплек-

са тока на ось d, т.е. ток i

, получим из (71.29) следующее выражение

для потокосцепления приведенной обмотки возбуждения:

= i

+ i

+ L

f σ

) + i

к d

. (71.41)

∼

–

– jα

–

Re I

∼

–

0,5 I

∼

–

∼

–

+()==

Re I

∼

–

0,5 I

∼

–

∼

–

+()==

αcos 0,5L

–

+()==

α 4π 3⁄+()cos 0,5L

–

+()==

++ 0,5 I

∼

+()L

0,5 I

∼

+()

477

Аналогичным образом выражаются через составляющие тока ста-

тора потокосцепления приведенных демпферных обмоток по соот-

ветствующим осям:

к d

= i

+ i

к d

+ L

к d σ

);

к q

= i

+ i

к q

+ L

к q σ

), (71.42)

где L

+ L

fσ

= L

; L

+ L

кdσ

= L

кd

; L

+ L

кdσ

= L

кq

— полные индук-

тивности приведенных обмотки возбуждения и демпферных конту-

ров по продольной и поперечной осям.

Результирующую комплексную функцию потокосцепления стато-

ра в (71.40) можно выразить через составляющие комплексных функ-

ций токов. Для этого достаточно в уравнении для (71.39) предста-

вить фазные потокосцепления в функции токов и индуктивностей

[(71.28) и аналогичные уравнения для Ψ

и Ψ

] и учесть изменение

индуктивностей в функции угла α (71.9), (71.17). Если, кроме того,

представить все тригонометрические функции в виде алгебраических

выражений, в которые входят только комплексные числа, то все необ-

ходимые преобразования можно провести в комплексной форме и

выразить результирующую комплексную функцию потокосцепления

статора следующим образом:

, (71.43)

где

= L

+ L

к d

; Ψ

= L

+ L

к q

— проекции результирующего комплекса на оси d или q ;

;

— проекции результирующего комплекса тока на оси d или q;

=3L

/2; L

= 3L

— главные индуктивности якоря по продольной и поперечной осям;

= L

+ L

; L

= L

+ L

— полные индуктивности якоря по продольной и поперечной осям;

= L

AAσ

– L

ABσ

— индуктивность рассеяния фазы якоря (с учетом влияния других

фаз).

∼

jΨ

∼

+()/2= i

-----

∼

–()=

478

После выражения комплексных

функций напряжения, тока и потоко-

сцепления в (71.40) через составляю-

щие по осям d и q это уравнение распа-

дается на два уравнения: уравнение

для составляющей напряжения стато-

ра по продольной оси и уравнение для

составляющей напряжения по попе-

речной оси:

(71.44)

Электрические величины, входя-

щие в (71.44), характеризуют процессы

в продольном и поперечном статорных

контурах, представляющих собой вра-

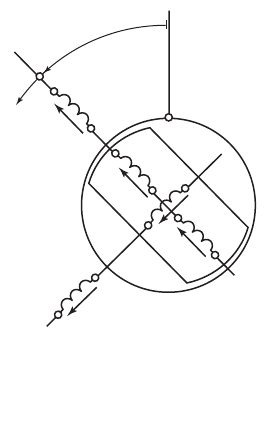
щающиеся трехфазные обмотки. Глав-

ные фазы этих обмоток с токами i

и i

, ориентированные соответст-

венно по направлению осей d и q, а также главные фазы приведенных

роторных контуров с токами i

, i

кd

, i

кq

показаны на рис. 71.8 (индекс

приведения опущен).

При исследовании переходных процессов (71.44) должны рассмат-

риваться совместно с уравнениями напряжений для роторных конту-

ров (71.26), записанными через приведенные величины (индекс при-

ведения «штрих», как и ранее, в этих и ряде других уравнений главы

опущен). Потокосцепления в (71.44) и (71.26) выражаются через со-

ставляющие токов по осями d и q по (71.41)—(71.43).

Рассмотрим совместно уравнения напряжений для продольных

роторных контуров (71.26) с учетом (71.41), (71.42) и уравнение для

продольного потокосцепления обмотки статора (71.43). Продиффе-

ренцировав последнее уравнение, получим следующую систему:

;

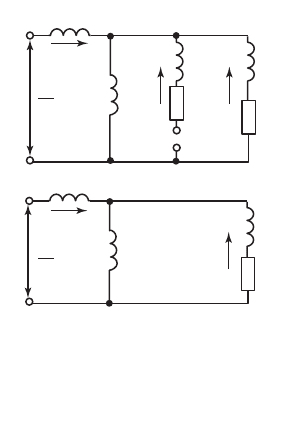
которой соответствует электрическая эквивалентная схема замеще-

ния по продольной оси, показанная на рис. 71.9, а.

dΨ

-----------

ωΨ

;–+=

dΨ

-----------

ωΨ

.++=

⎭

⎪

⎬

⎪

⎫

-----

кd

+()]+=

-----

кd

+()]++=

0 R

кd

-----

кd

+()]++=

²d

²q

Рис. 71.8. Главные фазы статор-

ных и приведенных роторных

контуров, ориентированных по

осям d и q

479

Поступая таким же образом с

уравнением напряжения для попереч-

ного роторного контура и с уравнени-

ем для поперечного потокосцепления

обмотки статора, получим электриче-

скую схему замещения по попереч-

ной оси, показанную на рис. 71.9, б.

Эти схемы отражают магнитные

трансформаторные связи между эк-

вивалентными контурами статора и

ротора, оси которых имеют соответ-

ственно продольное или поперечное

направление. Применение эквива-

лентных схем замещения по продоль-

ной и поперечной осям облегчает

анализ переходных процессов в син-

хронных машинах.

Преобразование дифференциаль-

ных уравнений синхронной машины

к осям d, q, 0 впервые получил в США Р. Парк в 20-х годах прошлого

столетия. Несколько позднее методы анализа переходных процессов

были развиты А. Горевым. В связи с этим преобразованную к осям d,

q, 0 систему уравнений синхронной машины (71.26), (71.27),

(71.41)—(71.44) называют уравнениями Парка—Горева.

Независимость коэффициентов при токах в (71.41)—(71.43) от уг-

лового положения ротора открывает возможность аналитического ис-

следования переходных процессов с помощью преобразованной сис-

темы уравнений, а также заметно облегчает программирование или

составление аналоговых схем при решении этих уравнений на цифро-

вых ЭВМ или АВМ. При аналитическом исследовании система пре-

образованных к осям d, q, 0 уравнений часто записывается и решается

в операторной форме. В этом случае символ производной d/dt заме-

няется оператором р.

71.7. Элетроманитный момент и равнение движения

ротора

Электромагнитный момент в синхронной машине может быть рас-

считан или как момент, действующий на ротор, или как момент, дей-

ствующий на статор. При расчете момента, действующего на статор,

можно воспользоваться формулами, полученными применительно к

асинхронной машине [см. (69.45)].

²dU

²qU

²d

²q

²d

²q

;

б)

Рис. 71.9. Эквивалентные схемы

замещения синхронной машины

по продольной (а) и поперечной (б)

осям