Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.

78
)0Tn2(wx
11
n
++=
τ
при
α
=
1
τ
.
Аналогично, для сохранения непрерывности по
2
τ
α
→ будем считать
)0T2Tn2(wy
22
n
+−+=
τ
при
2
τ
α
= .
Наконец, когда происходит совпадение всех точек
τ
1
=
τ
2
=
α
динамика
переменных в дискретной модели (2. 4) заключается в следующем:
а) в точке вида 2Tn+
α
сначала происходит переменной скачок переменной
w
1
, а затем - скачок переменной w
2
(с учетом полученного значения w
1
);
б) в точке 2Tn+2T-
α
сначала происходит скачок переменной w
2
, а затем –
скачок переменной w
1
(с учетом полученного значения w
2
) .
Здесь, как и ранее, удобно обозначить:
n
x
- значение скачка переменной w
1
в точке 2Tn+
α
;
n
y
- значение скачка переменной w
2
в точке 2Tn+2T-
α
.
На примере отображения приведем явные формулы. Здесь
:Q
1
)y,x()y,x(
0100
→
1
Q расщепляется в композицию четырех элементарных отображений:
1) на I
1
=[
α
, 2T-
α
) переменная w
1
экспонентциально убывает, поэтому
π
1
:
x
→
x exp(2
α
-2T);
2) в I
2
=точке [2T-
α
] происходит скачок переменной w
1
, который
описывается функцией S (см. раздел 3.1)
π
2
:
x
→
S(x, y
0
);
3) на I
3
=(2T-
α
, 2T+
α
) переменная w
1
экспонентциально убывает, поэтому
π
3
:
x
→
x exp(-2
α
);
4) в I =точке [2T+
4
α
] происходит скачок переменной w
1
, поэтому
π
:
x
→
S(x, y
0
exp(-2
4
α
)).
Аналогичное разложение имеет место и для .
:Q
2
)y,x()y,x(
1101
→
Данную систему с предельно близкими точками роста популяций (т.е.
21
τ
α
τ
== ) обозначим через . Поскольку все элементарные отображения –
непрерывные функции от
τ
1
,
)(DD
*
α
2
τ
и
α
, то и непрерывно зависят от
указанных параметров и при выполнении более сильного допустимого условия:
1
Q
2
Q
τ
1
≤
α
≤
τ
2
.
Дискретные соотношения (2. 4) определяют отображение
79
Λ
: (x
n
, y
n
)
→
(x
n+1
, y
n+1
),
которое расщепляется в композицию простых (изменяющих лишь одну
координату) отображений:
(x
n
, y
n
)
→
(x
n+1
, y
n
)
→
(x
n+1
, y
n+1
).
Согласно утверждению 3.5 каждое простое отображение является монотонно
возрастающей и выпуклой вверх функцией.
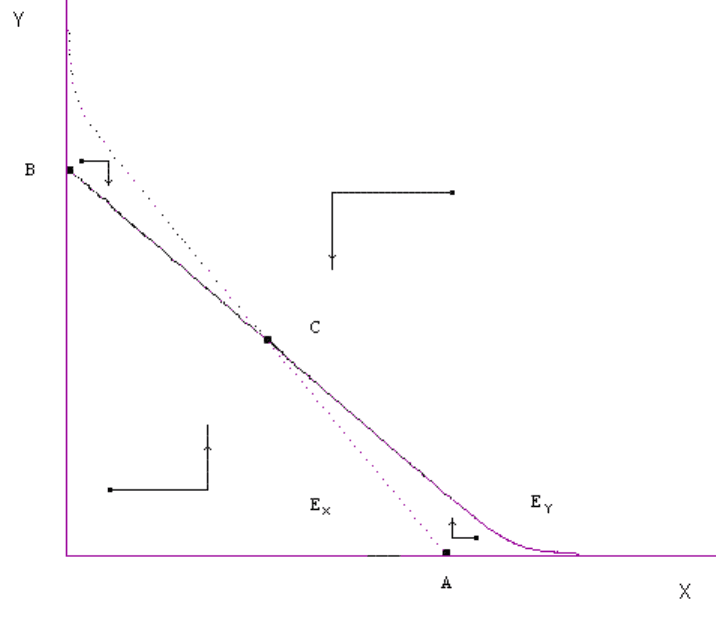
В первом квадранте фазовой плоскости (x, y) построим изоклину E
x
, которая
задается соотношением
x=Q
1
(x, y) (2. 5)
при x>0. Оказывается, при достаточно малых значениях y
≥ 0 положительное
решение x в (2. 5) существует. Само решение x=q
1
(y) является убывающей
функцией.
Рис. 3.4а. Пересечение изоклин при эволюционно - устойчивом параметре
α
. \
Аналогично, изоклина E
y
определяется уравнением
y=Q
2
(y, x),
которое при достаточно малых
0
x
≥
имеет положительное решение – убывающую
функцию y=q
2
(x).

80
Кроме того, функции и непрерывно зависят от допустимых
параметров
τ
1
,
1
q
2
q
τ
2
,
α
. На рис. 3.4а изоклина E
x
выходит из равновесной точки A=(x
*
,
0, а изоклина E
y
выходит из равновесной точки B=(0, y
*
).
Проведем две серии численных экспериментов с дискретной моделью (2. 4).
Здесь будем считать
1
T
=
и
3)(
=
τ
μ
для всех
τ
.
В первом эксперименте установим существование ЭУ - параметров
τ
. С
помощью модели DD
*
( ) построим изоклины E
*
и E
*
. Оказывается, они
пересекаются в положительной точке (см. рис. 3.4а). Данная точка является
устойчивым равновесием соответствующей системы (2.4).
2/T
x
y
*
C
Покажем, что значение является ЭУ - параметром. Действительно,
пусть имеется исходная популяция - носитель параметра и мутант - носитель
параметра (
2/T
*
=
τ
*
τ
ετ
+
*
ε
- мало). Для примера считаем
ε
>0, поэтому на [0,T] первой
совершает скачок исходная популяция ( , а затем – мутант (
)x
y
). Построим здесь
изоклины и , которые , в силу непрерывности по
x
E
y
E
ε
, будут мало отличаться
от соответствующих E
*
и E
*
. Поэтому новые изоклины тоже пересекаются. При
малом возмущении равновесной точки
x
y
≈
возникает переход в
положительную точку . Иными словами, при возникновении мутанта не
происходит вымирания исходной популяции.
)0,x(
*
C
≈
*
C
Аналогично, и при
ε
<0 устанавливаем сосуществование мутанта (
x
) и
исходной популяции ( .
)y
В силу непрерывности по
1
τ
и
2
τ
, достаточно малая окрестность точки
состоит сплошь из ЭУ - параметров. Такие ЭУ - параметры естественно
называть плотными.
2/T
*
=
τ
Обсудим изложенный выше прием, связанный с предельным переходом по
параметрам
1
τ
и
2
τ
. Пусть при 2/T
1
=
τ
,
ε
τ
±
=
2/T
2
и конкретном
ε
численно
установлено сосуществование исходной популяции и мутанта. Без использования
нельзя гарантировать того, что сосуществование популяций будет иметь
место и при меньших значениях
)2/(
*
TDD
ε
. Поэтому расчеты с предельным значениями
1
τ
и
2
τ
, по сути, необходимы.
81
Дополнительные компьютерные расчеты неожиданно показали, что точка
оказывается универсальным, плотным ЭУ - параметром и при других
(достаточно больших) функциях
2/T
*
=
τ
)(
τ
μ
. Докажем это строго, используя следующие
два вспомогательных технических утверждения (Ильичев, 2006б).
Лемма 3.6. Изоклина E
x
является графиком убывающей дифференцируемой
функции , определенной на некотором промежутке
)(
1
yqx =
),0[ y
)
. Функция
непрерывно дифференцируемо зависит от допустимых параметров
1
q
1
τ
,
2
τ
,
α
.
Лемма 3.7. Пусть значение
)2/T(
μ
велико и 2/T
21
==
τ
τ
. Тогда
"основание" изоклины меньше её "высоты".
*
x
E
Аналогичное утверждение имеет место и для изоклины .
*
y
E
Отсюда следует, что изоклины и пересекаются в одной или
нескольких точках . Пусть П – наименьший прямоугольник в , содержащий
все точки пересечения изоклин. Тогда каждая положительная орбита системы (2.4)
устремляется к П. Поэтому возникает устойчивое сосуществование исходной
популяции и мутанта. В силу непрерывности, такая ситуация сохраняется и при
малой деформации параметров
*
x
E
*
y
E
2
R
+
2
R
+
1
τ
,
2
τ
. Таким образом, справедливо
Утверждение 3.6. Пусть
)(
τ
μ
велика для всех
τ
, а Δ − малая окрестность
точки . Тогда любой параметр
τ
из Δ является эволюционно - устойчивым. 2/T
Во втором эксперименте установим существование
τ
, не являющегося ЭУ -
параметром. Опять – таки, с помощью модели построим изоклины и
(см. рис. 3.4б). Оказывается, изоклина находится ниже . Это означает,
что вытесняет
)1.0(DD
*
*
x
E
*
y
E
*
x
E
*
y
E
y
x
. В силу непрерывности по
ε
, исходная популяция (
x
) с
параметром
1.0=
τ
вытесняется мутантом (y ) с параметром
ε
τ
+= 1.0
, где
ε
-
малое положительное число. Поэтому
1.0
=
τ
не является ЭУ – параметром.
На циклической шкале времени численно построены все ЭУ – параметры
τ
при
3)( ≡
τ
μ
и 1
T
= . Они составляют открытый интервал (1/3, 2/3).
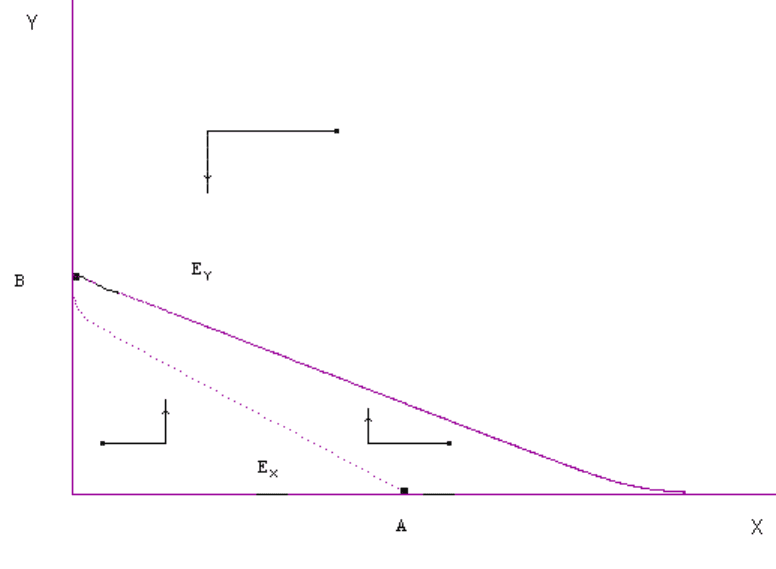
82
Рис. 3.4б. Когда изоклины не пересекаются,
α
не является эволюционно -
устойчивом параметром.
Если же исходная популяция (с параметром
τ
) порождает двух мутантов с
параметрами
ε
τ
− и
ε
τ
+ , то в рамках DD -систем эволюционно – устойчивых
параметров
τ
не обнаружено.
3.3. D-система Вольтерра. Условия существования и отбор
В рамках данной схемы динамика близких конкурентов представляется в
форме (Ильичев, 1996 и 1998а):
(
)
(
)
[]
()( )
[]
,1
,1
1
11111
nnnnn
n
xxtxx
xxtxx
++−−=
+
+
−
−=
K
&
KKKKKKKKKKKKKKK
K
&
τδμ
τ
δ
μ
(3.1)
где и для всех ;
0>μ
i
0
0
>
i
x
i
T
n
<
τ
<
<
τ
<
τ
<
K
21
0 ; является
δ
T
-
периодической дельта -функцией. Данную модель назовем D –системой Вольтерра.
План исследования (3.1) во многом аналогичен анализу D -системы Контуа,
поэтому ниже изложим без доказательства лишь основные этапы.
Предварительно рассмотрим динамику отдельной популяции
(
)
(
)
[
]
kxtxx
+
τ
−
μ
δ
−
=
1
&
,

83
где и – положительные константы. Очевидно, при
μ
k
m
T
t +≠
τ
решение
является возрастающей экспонентой. В точках разрыва “сверху-вниз“ выполняется
соотношение
()
(
)
kxx
μ
ϕ
ϕ
−
=
−+
, (3.2)
где
()
(
)
kzzz +−= lnln
ϕ
. А отображение Пуанкаре имеет вид
()
[
]
(
)
mm
yTkkky −+−=
+
μμ
exp1exp1
1
. (3.3)
Рекурсия (3.3) задает возрастающую и выпуклую вверх функцию
(
)
mm
ygy =
+1
. При
Tk <
μ
данная последовательность сходится к некоторой
положительной предельной точке.
В системе (3.1) при
i
mTt
τ
+
≠
- тая переменная является возрастающей
экспонентной. Положим
i
(
)
0+τ+=
ii
m
i
mTxy
, тогда, используя соотношение скачка
(3.2), получаем
(
)
mmmmm
yTcccy
111111
1
1
exp/]1)[exp(1 −+−=
+
μμ
,
(3.4)
где – суммарная численность остальных популяций;
∑
=
=
n
j
m
jj
m
ybc
2
11
(
)
jj
Tb τ−τ+=
11
exp
для всех
1>
j
. Уравнение (3.4) определяет «простое»
отображение
(
)
(
)
m
n
mmm
n
mm
yyyyyyG ,,,,,,:
2
1
1211
KK
+
→
.
Здесь действует только на первый аргумент. Обозначим соответствующую
функцию
1
G
(
)
m
n
mmm
yyygy ,,,
211
1
1
K=
+
.
Для описания динамики остальных переменных построим матрицу
взаимодействий Вольтерра
(
)
:
ijn
bB
=
(
)
()
⎪
⎩
⎪
⎨
⎧
=
<−+
>−
=
ji
jiji
jiji
ij
Tb
ττ
ττττ
ττττ
если,0
,если,exp
,если,exp
Теперь для получаем аналогичные соотношения
1>k
(
)
m
k
m
kk
m
k
m
kk
m
k
yTcccy −+−=
+
μμ
exp/]1)[exp(1
1
,
(3.5)
где .
∑∑
+=
−
=
+
+=
n
kj
m
jkj
k
j
m
jkj
m
k
ybybc
1
1
1
1
84
При уравнение (3.5) также задает «простое» отображение 1>k
(
)
(
)
(
)
nknkk
yYgyyyyG ,,,,,,,,:
11
KKKK →
,
которое влияет только на «свою» ( -ю) переменную.
k
Лемма 3.8. Каждая функция возрастает по "своей" переменной
i
g
(
)
i
y и
убывает по всем остальным – "чужим" переменным.
И здесь отображение Пуанкаре (P) системы (3.1) допускает расщепление в
композицию "простых" отображений
1
GGP
n
oKo
=
.
Ниже важное значение будут иметь свойства функции
()
(
)
[]
(
)
[
]
1expexp1
−
−
−
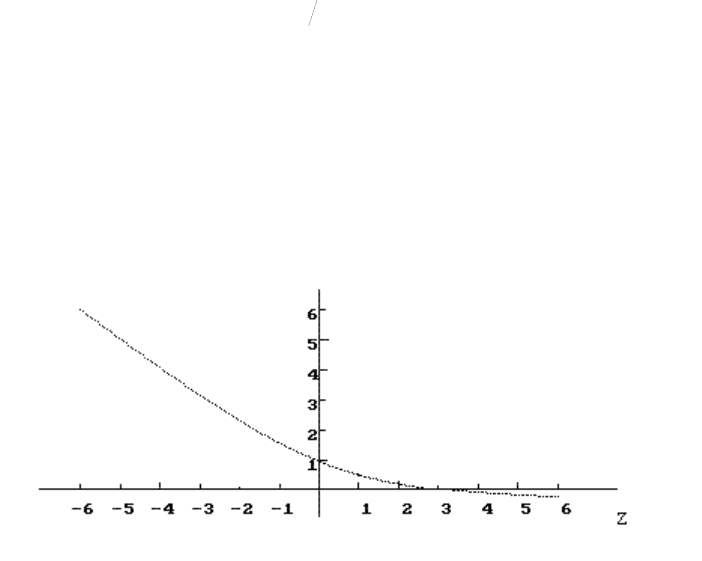
= zTzzzf , (3.6)
где
0>
T
. При определим из соображений непрерывности, положив
. Имеет место элементарная (см. рис. 3.5)
0=z f
() ( )
Tf −−= exp10
Лемма 3.9. При
T
z
<
<∞−
функция f(z) является монотонно убывающей и
выпуклой вниз.
Рис. 3.5. График функции при
()
zf
3
=
T
.
На фазовой плоскости определим семейство "изоклин"
n
R
+
(
)
{
}
YYGYE
ii
=
=
| ,
где . Уравнение
ni ,,1 K=
(
)
Ygy
ii
=
, в котором
(
)
n
yyyY ,,,
21
K
=
, представляет
собой эквивалентный способ задания изоклины. Пусть точка
Y
принадлежит ,
тогда из (3.4) и (3.5) выводимо соотношение
i
E
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∑
=
n
j
jijiii
ybfy
1
μμ
.
Из леммы 3. 9 следует, что – выпуклая вниз поверхность в . Она разбивает
i
E
n
R
+

85
n
R
+
на две связные части, одна из которых ("нижняя") ограничена и примыкает к
началу координат. Очевидно, точка
Y
лежит ниже , когда имеет место
неравенство . В этом случае имеет место .
i
E
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
<
∑
=
n
j
jijiii
ybfy
1
μμ
()
ii
yYg >
Лемма 3.10. Пусть точка
Y
лежит ниже , тогда и ) лежит ниже
. А если точка
i
E
()
YG
i
i
E
Y
лежит выше , то и
i
E
(
)
YG
i
лежит выше .
i
E
Теперь определим условия, при оторых
1
располагается выше всех
остальных . Отметим, что пересечение изоклин с осями координат легко
вычисляется. Так, при
3=
для изоклины
1
E
получа
к
ем
)]exp(1[ Ty −−= /(
1
*
2
Ty
μ
= .
bTy
μ
=
.
R
>
E
i
E
n
1
/
μ
, )
12
b ,
*
1
)/(
131
*
3
bTy
μ
=
А для изоклины находим
2
E
)/(
212
**
1
bTy
μ
= , ,
**
3
2
**
2
/)]exp(1[
μ
Ty −−=
)/(
232
Здесь ,
**
- пересечение i - той оси координат с изоклинами и ,
соответственно. Представляется весьма неожиданной
*
i
y
i
y
1
E
2
E
Лемма 3.11.
Если изоклина
E лежит ниже на "своей" оси
i
O , то
лежит ниже
1
всюду в
n
+
.
i 1
E Y
i
E
E
Отметим, что
1]1)[exp( /
−
T
и
место условие запаса
T
для всех
0>T
. Оказывается, есл для
некоторого
1>i
имеет
(
)
[
]
TT
i
1exp
1
−
>
μ
μ
, (3.7)
тогда на оси точка пересечения лежит выше соответствующей точки
пересечения . С учетом предыдущей леммы легко получаем
i
OY
тогда изоклина
E лежит выше всех остальных
1
E
i
Лемма 3.12. Пусть для всех выполняется соотношение запаса (3.7),
E
1>i
{
}
i +1
E в ,
Далее, при из функция
n
R
z
(
]
T,∞−
(
)
zf
изменяется во всем диапазоне
[
)
∞
+
,0
.
Поэтому для всех аргументов из определена функция
+
R
ϕ
– обратная к . Тогда
может быть задана иным уравнением
=
n
jijiii
yby
μμϕ
.
Теперь определим в непрерывную, неотрицательную функцию:
f
1
E
()
∑
=j 1
n
R
+
86
() ( )
⎭
⎬
⎫
⎩
⎨
⎧
=
∑
=
n
j
jj
ybyYL
2
1111
,max
μμϕ
.
Если
()
0,,0,
1
KyY = и
(
)
[
]
1
xp
1
e1
μ
−
−
≥y T
,
то
(
)
0
=
YL
Отметим, что .
(
)
YL
состоит из кусков аналитического представления
1
E . При выполнении условии
са (3.7) для всезапа х справедлива
1>i
Лемма 3.13.
На орбите дискретной D-системы Вольтерра функция
(нестрого) убывает. При этом
L
(
)
(
)
(
)
YLYPPL
<
для
Y
из
n
.
R
+
Отсюда сразу вытекает
Утверждение 3.7.
Пусть в D-системе Вольтерра выполняется условие
запаса (3.7) для всех
1>
. Тогда первая популяция вытесняет остальны
i
е.
Существование универсальных констант в схемах Контуа и Вольтера
обусловлено конкуренцией ”все против всех”. В моделях ”все против одного”
константа запаса зависит от
n
.
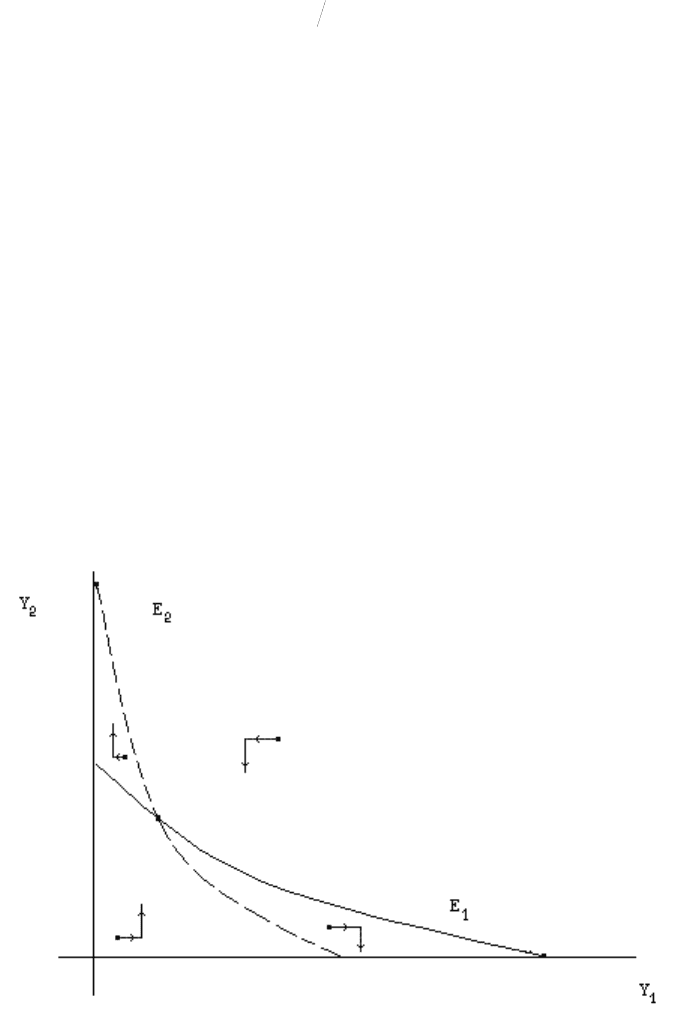
Рис. 3 е положительное равновесие в D-системе Вольтерра. .6. Неустойчиво
При
2
=
n
определим геометрические условия существования
положительного равновесия в дискретной D-системе Вольтерра. В силу леммы
3. 11, каждая изоклина должна лежать выше другой на "своей" оси координат (рис.
3.6). Поэтому равновесная точка – седло. Вероятно, и в многомерном случ е
положительное равновесие (если оно существ
а
ует) в D-системе Вольтерра будет
87
неусто
жесткой (и более сложной), чем в схеме Конт .
Мы живем в мире нелинейных явлений. В это связи представляется весьма
ли динозавров: “они были слишком
линей ” (Мол
а популяций в
перем
Пример 1. Рассмотрим модификацию модели т инсона с запаздыванием
йчивым. Поэтому конкуренция в схеме Вольтерра оказывается более
уа
Обсуждение.
й
правдоподобной математическая версия гибе
ны для изменяющихся условий среды чанов, 1992). Выше было
продемонстрировано, что с помощью периодических дельта - функций возможен
достаточно полный нализ сложной нелинейной динамики
енной среде. Приведем еще два примера.
Ха ч
)]()(1[ atxtxx
−
−
+
−
=
τ
δ
&
,
где
T
a <<0
. Положим , тогда неожиданно
получаем дискретную модель Риккера с ”горбатой правой частью”
.
)0TmT(x)aTexp(y
m
++−−=
τ
)yTexp(yy
1m1mm −−
−=
При
73.2≈
T
здесь возникают хаотические .
Отметим, что в гладких моделях вида
режимы
),( txfx
=
&
сдвиг – отображение всегда
оказывается монотонно возрастающим отображением, и тогда соответствующая
динамика переменной
x
обладает достаточно простым поведением.
ример 2. Рассмотрим модификацию модели Вольтерра “хищник - жертва” П
xxytx
−
−
= )(
1
τ
δ
&
, xytyy )(
2
τ
δ
−
−
=
&
,
где
<0
T<<
21
τ
τ
. Положим
)()exp(
121
+−=
τττ
mTxX
m
и
)0()exp(
221
++−+=
τττ
mTyTY
.
Тогда выводимы соотношения
mm
0+
Y
m
m
X
X
T
+
−
= ,
+
lnln
1 11
ln
++
−ln
+
=
mmm
X
T
YY .
В данной искретной модели равновесие
T
Y
X
=
=
**
д неустойчиво при всех
0>
T
.
При
=
T
1 в 6.
Другой пример эффективного использования дельта – функций рассмотрен в
работе
е. Об
озникает локально устойчивый цикл длины
(Недорезов, Утопин, 2003).
3.4. Приложени основание основных результатов
