Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.

58
которых одновременно выполняются условия:
1)
()
PA −
– устойчивая матрица;
2)
имеет место хотя бы одно из неравенств
221
ap или
112
ap . d > d >
Тогда нулевое равновесие (2.2) стабилизируемо при подходящем выборе и .
1
q
2
q
Доказательство леммы П.2
. Пусть параметры и выбраны согласно
первому условию леммы П. 2. Тогда корни и уравнения
1
p
2
p
1
z
2
z
0
=
−
− zEPA
лежат в ЛКП. При данных и рассмотрим промежуточную систему:
1
p
2
p
(
)
()
.
,
,
11111
22221212
1121211111
sqxps
xpaxax
sqxaxpax
−=
−+=
+
+
−
=
&
&
&
(П. 6)
В (П. 6) по сравнению с (2.2) оставлено пассивное состояние лишь для переменной
. Соответствующий для (П. 6) характеристический многочлен имеет вид:
1
x
0
0
0
11
22221
112111
=
−−
−−
−−
zqp
zpaa
qazpa
. (П.7)
При уравнение (П.7) имеет нулевой корень
0
1
=q
(
)
0
3
=
z , а также корни и ,
принадлежащие ЛКП (см. выше). Очевидно, при малом изменении корни и
остаются в ЛКП. Определим
условия, при которых корень переходит в ЛКП
при малом увеличении . Продифференцируем определитель (П.7) по параметру
, воспользовавшись следующей формулой (Ланкастер, 1982, стр. 49):
1
z
2
z
1
q
1
z
2
z
3
z
1
q
1
q
(
)
(
) ()
nnn
bDbbbDbbD ,,,,
111
KKKK
+
+
=
, (П.8)
где – вектор - столбцы определителя
i
b
n
bbb K
21
;
D
– оператор
дифференцирования по параметру . В данном случае при и в сумме
(П.8) все определители, кроме последнего, равны нулю. Окончательно получаем
1
q 0
3
=z 0
1
=q
0
10
0
1
31
22221
12111
=
−−
−
−
Dzp
paa
apa
,
где
133
qzDz ∂∂= . Отсюда после элементарных преобразований находим
[
]
(
)
211123
, ppddapDz
−
=
.
Так как – устойчивая, то
(
PA −
)
(
)
0,
21
>ppd . Следовательно, при условии
59
dap
<
112
(П.9)
имеем . Значит корень оказывается в ЛКП.
()
0Re
3
<Dz
3
z
Рассмотрим теперь характеристическое уравнение для системы (2.2). Если
, то уравнение имеет корень
0
2
=q
0)( =zH
0
4
=
z . При условии (П.9) и малом
остальные корни находятся в ЛКП. Покажем, что при малом
увеличении корень также оказывается в ЛКП. Для
этого
продифференцируем уравнение
0
2
=q
321
,, zzz
2
q
4
z
0)(
=
zH
по параметру . При и
2
q 0
2
=q 0
4
=
z в
соответствующей сумме (П.8) все определители, кроме
последнего, равны нулю.
Окончательно получаем
0
100
00
10
0
42
11
22221
112111
=
−−
−
−
−
Dzp
qp
paa
qapa
,
где
244
qzDz ∂∂= . Отсюда после элементарных преобразований находим
[]
dapdDz −=
1124
. Так как и выполняется условие (П.9), то 0>d
(
)
0Re
4
<
Dz .
Итак, при малых положительных корень также оказывается в ЛКП.
2
p
4
z
Аналогичное рассуждение, использующее другую промежуточную систему
и , приводит ко второму достаточному условию стабилизации
. Лемма П.2 доказана.
(
21
, xx
)
2
s
(
dap <
221
)
В силу данной леммы, для стабилизации нулевого равновесия в системе
(2.2) достаточно установить существование положительных и ,
удовлетворяющих одновременно условиям:
1
p
2
p
(
)
(
)
112221
2112222111222111
или)2
и0)1
apdapd
aapapapapa
>>
>
−
−
<
−
+−
. (П. 10)
Данный анализ существенно зависит от знаковой структуры матрицы A.
Оказывается, что за исключением "плохого" случая (2.3) система (П. 10) совместна
при подходящем выборе положительных и .
1
p
2
p
В работе Ильичева (1995в) установлено, что в "плохом" случае (т.е. при
соблюдении всех неравенств (2.3)) характеристическое уравнение для системы
(2.2) обязательно имеет положительный корень при любых (положительных)
управляющих параметрах
{
и
}
i
p
{
}
i
q .

60
Идея доказательства утверждения 2.7. Рассмотрим функцию (3.7) для всех
неотрицательных переменных . Функция равна только в точке
равновесия
}s,x{
ii
L
0
r
. Наибольший аргумент операции
ma
x
(на нем реализуется ) будем
называть главным. В “очень хороших” точках у лишь один аргумент является
главным, и тогда данная функция оказывается дифференцируемой. Ниже будем
использовать следующие достаточные условия строгого роста переменных в
системе (3.7) при :
L
L
2n =
если
i21
cxx
<
+ и 0qspx
iiii
>
+
−
, то ; 0x
i
>
&
если
0qspx
iiii
>
−
, то . 0s
i
>
&
Строгая убыль переменных возникает при противоположных неравенствах.
Теперь покажем, что в хороших случаях строго убывает:
L
G1.
0xcL
11
>
−
= . Здесь имеем
211
xxc
+
> , и значит . Кроме
того, из
0)xx(f
211
>+
111111
p/qscxc −>−
следует
1111
p/qsx
<
. Поэтому имеет место
и .
0x
1
>
&
0xL
1
<−=
&
&
G2. 0cxL
11
>
−
= . Тогда заведомо 0)c(f)xx(f
11211
=
<
+
и .
Следовательно . Отсюда получаем .
1111
p/qsx >
0x
1
<
&
0xL
1
<=
&
&
G3.
0p/qscL
1111
>
−
= . Тогда получаем
1111
xp/qs
<
, откуда следует
0s
1
>
&
и . 0/
111
<−= pqsL
&
&
G4. . Этот вариант разбирается аналогично G3, но с
противоположными знаками в неравенствах. Итак,
0cp/qsL
1111
>−=
0s
1
<
&
и . 0/
111
<= pqsL
&
&
G5. . Здесь из
0xL
2
>=
112
xcx
−
>
следует
2121
ccxx >>
+
, и значит
. Кроме того, , поэтому
0)xx(f
212
<+
2222
p/qsx > 0x
2
<
&
и .
0xL
2
<−=
&
&
G6. . Отсюда получаем . Поэтому имеет место
и .
0p/qsL
222
>=
2222
xp/qs >
0s
2
<
&
0<L
&
Теперь рассмотрим “плохие” фазовые точки, где значение реализуется на
двух (и более) аргументах операции
L
ma
x
. Здесь производная главных аргументов
может быть отрицательной или равняться
0
.
Если производные всех главных аргументов меньше нуля, то как верхняя
огибающая конечного набора строго убывающих функций будет строго убывать.
L

61
Этот случай можно считать “хорошим” А в некоторых “очень плохих” точках
производные некоторых главных аргументов равны . Оказывается, за
исключением “вырожденных” точек вида
0
0sx
11
=
=
и 0s,0x
22
≥≥
такая ситуация может длиться лишь “мгновение”, после чего значения главных
аргументов становятся различными. Грубо говоря, система (3.6) “мгновенно”
переходит из “очень плохой” фазовой точки в “хорошую”.
В работе (Ильичев, 2008) показано, что
вырожденная точка вида не может
быть предельной для траекторий (3.4). Поэтому функция строго убывает до
некоторого значения
L
A
. Предположим , тогда используя процедуру
проталкивания предельной точки, легко получаем противоречие. Поэтому
0A >
0A
=
, и
значит утверждение 2.7 доказано.
Идея доказательства утверждения 2.8
. Покажем, что функция (3.8)
убывает на траекториях (3.6) из малой окрестности равновесия
r
. Сначала
рассмотрим хороший случай, когда
0
L
>
реализуется только на одном из
аргументов операции
ma
x
.
W1.
)1n(
xc
L
11
−
−
=
. Тогда после складывания всех неравенств вида
( получаем
i
xL >
)n,...,2i =
n11
x...xc
+
+
> . Значит, . Далее, из 0)S(f
1
>
1n
p/qsc
L
1111
−
−
>
следует 0qspx
1111
>
+
− . В целом, находим .
0)1n/(xL
1
<−−=
&
&
W2.
)1n(
cx
L
11
−
−
=
. Тогда и, значит,
11
cx > 0)S(f
1
<
. А из
1n
cp/qs
L
1111
−
−
>
следует . В целом, находим .
0qspx
1111
<+−
0)1n/(xL
1
<−=
&
&
W3+W4.
1n
q/psc
L
1111
−
−
=
. Этот случай разбирается аналогично вариантам G3
и G4 из обоснования утверждения 2.7.
W5. для . Поскольку фазовая точка находится вблизи равновесия
i
xL =
2i ≥
r
, то и, значит, . Далее, из следует
i
cS > 0)S(f
i
<
iii
p/qsL > 0qspx
iiii
<
+− .
Поэтому .
0xL
i
<=
&
&
W6. для . Из получаем
iii
p/qsL =
2i ≥
i
xL > 0qspx
iiii
<
−
и, значит,

62
0p/qsL
iii
<=
&
&
.
В плохих точках функция может иметь сразу несколько главных
аргументов. Здесь производная главных аргументов может быть отрицательной
или равняться . Если производные всех главных аргументов меньше нуля, то
как верхняя огибающая конечного набора строго убывающих функций будет
строго убывать. А в некоторых “очень плохих” точках производные некоторых
главных аргументов могут быть равны . Определим условия, при которых
возникает такая ситуация. Анализ удобно проводить в следующем порядке:
L
0
L
0
Z5. и для . Согласно неравенствам пункта W5 данное
соотношение невозможно, если
i
xL = 0x
i
=
&
2i ≥
0xL
i
>
=
. Здесь всегда имеет место 0x
i
<
&
.
Z6. и
iii
p/qsL = 0s
i
=
&
для . Это возможно лишь при условии
. Тогда также является главным аргументом. В силу пункта Z5,
начнет “мгновенно” убывать. Поэтому приведенное выше необходимое условие
нарушается, и спустя “мгновение” тоже будет убывать.
2i ≥
iiii
xp/qs =
i
x
i
x
i
s
Z2.
)1n(
cx
L
11
−
−
=
и 0x
1
=
&
. Поскольку , то согласно неравенствам
пункта W2 данное соотношение невозможно. Здесь всегда имеет место
11
cx >
0x
1
<
&
.
Z1.
)1n(
xc
L
11
−
−
= и 0x
1
=
&
. Из неравенств пункта W1 следует, что тогда
должны, по крайней мере, выполняться неравенства
i
xL
=
для всех . Ввиду
рассуждения из пункта Z5, все такие начнут “мгновенно” убывать. Спустя
“мгновение” это вызовет рост .
2i ≥
i
x
1
x
Z3+Z4.
1n
q/psc
L
1111
−
−
=
и 0s
1
=
&
. Это возможно лишь при
1111
p/qsx
=
,
но тогда главным аргументом является и
1n
xc
L
11
−
−
=
. В силу пунктов Z1 и Z2,
переменная “мгновенно” начнет изменяться. Затем “мгновенно” изменится и
переменная .
1
x
1
s
Иными словами, плохая ситуация может длиться лишь “мгновение”, после
чего значения главных аргументов становятся различными. Последнее. Применяя
процедуру проталкивания предельной точки, устанавливаем:
0
L
→
.
63
ГЛАВА 3
АНАЛИЗ СПЕЦИАЛЬНЫХ МОДЕЛЕЙ КОНКУРЕНЦИИ
С ПЕРИОДИЧЕСКОЙ ДЕЛЬТА - ФУНКЦИЕЙ В ПРАВОЙ ЧАСТИ
Особую роль играет … фундаментальное
решение – как “наименее сингулярное”
среди всех сингулярных решений.
(Юдович. В.И. Лекции об уравнениях
математической физики. 2 часть.)
Исследование глобальной динамики конкурентов в периодической среде
связано с трудным анализом систем неавтономных, нелинейных
дифференциальных уравнений (Дегерменджи, 1976; Cushing, 1980; De Montoni,
Schiaffino, 1981; Gatto, Annaratone, Borghesi, 1979; Smith, Waltman, 2000). Здесь
методологически важно разработать эффективный план “движения от простого к
сложному”. Так, сильные упрощения возникают, если в качестве скоростей роста
конкурентов использовать периодические дельта – функции. В таких специальных
моделях (D - системах) от "полноценного" нелинейного взаимодействия остается
лишь некоторый "нелинейный скелет", тем не менее, сохраняющий конкурентную
суть явлений.
3.1. D- система Контуа. ”Парадоксы“, сосуществование и отбор
Для проведения анализа неавтономных моделей, зачастую, переменные
коэффициенты выбирают кусочно-постоянными функциями (Armstrong and
Mc.Gehee, 1976). Такой подход связан с громоздкими выкладками, и далеко не
всегда приводит к цели. Ниже предлагается более содержательная техника,
навеянная конструкцией “игольчатых вариаций” из теории оптимального
управления (Понтрягин, 1989) и теоремой Крейна- Мильмана из выпуклого анализа
(Фелпс, 1968). Рассмотрим модель динамики одной популяции
x
&
=xf(x,
β
(t)), (1.1)
где x – неотрицательная численность; гладкая и убывающая по
x
функция f
характеризует негативное действие внутренней конкуренции;
β
-
неотрицательная скорость роста, зависящая от текущих условий среды (например,
температуры).
64
Пусть температура T - периодически изменяется, тогда и
β
(t) является T –
периодической функцией. Без ограничения общности можно считать, что интеграл
от
β
(t) на отрезке [0,T] равен 1. В этом случае требования на
β
(t) формально
совпадают с ограничениями на функцию веса из главы 1. Используя приведенные
там эвристические соображения, можно полагать, что и здесь дельта-функции
составляют (в некотором смысле) базис.
Итак, в качестве
)(t
β
выберем
−
T
периодические дельта - функции. А
именно, для всех t из [0,T] положим
β
(t)=
δ
(t-
τ
) при 0<
τ
<T, и далее будем считать
β
(mT+t)=
β
(t) для всех целых m.
Напомним (Филиппов, 1985), что здесь под решением уравнения
(
)
)(,
τ
−
δ
=
txfxx
&
(1.2)
на отрезке
[
подразумевается поточечный предел семейства решений
]
T,0
(
)
)(,
τ
δ
−
=
txfxx
nnnn
&
(1.3)
где для всех ; – так называемая дельтаобразная последовательность
функций, которые удовлетворяют условиям:
0
0
xx
n
=
n
{}
n
δ
а) каждая функция
(
)
s
n
δ – гладкая и положительна при из интервала
. Вне интервала функция
s
[
nnn
baI +τ−τ= ,
]
n
I
n
δ
равна нулю. Величины ,
–
положительны и стремятся к при
n
a
n
b
0
∞
→n ;
б) интеграл от функции
n
δ
на каждом отрезке равен
1
.
n
I
Существует много способов построения таких последовательностей.
Величина в (1.2) считается корректно определенной, если предел в
(1.3) существует и не зависит от выбора последовательности
{}
.
)(tx
)}({ tx
n
n
δ
Для биологических приложений вполне достаточно моделей (1.2), в которых
функция представляется в форме
f
(
)
(
)
(
)
xhtxg
τ
δ
−
+
.
Здесь – не возрастающая и – знакоопределенная строго убывающая
гладкие функции. В этом случае уравнение (1.2) приобретает вид
)(xg )(xh
(
)
(
)
(
)
[
]
xhtxgxx
τ
δ
−
+
=
&
,
где . Очевидно, при всех
0
0
≥x
τ
+
≠
m
T
t
решение данного уравнения определено
корректно. В точках разрыва существуют пределы слева и справа. Отметим, что в

65
точке
τ=
t
значение
x
может зависеть от выбора дельтаобразной
последовательности
{
(Ильичев, Брискин, 1989).
}
n
δ
Теперь выведем формулу для вычисления скачка в точке разрыва
τ
=
t
.
Пусть
}{
n
δ
– произвольная дельтаобразная последовательность. Рассмотрим
решение уравнения
(
)
[
]
(
)
(
)
(
)
τ
−
δ
=
−
txhxgxhxx
nnnnnn
&
на малом отрезке
[
nn
ba +−
]
τ
τ
, . Тогда интеграл от непрерывной и ограниченной
функции
hg мал и стремится к нулю при
∞
→n . В пределе получаем уравнение
разрыва
(
)
(
)
1
=
−
−+
xx
ϕ
ϕ
, (1.4)
где
()
x
ϕ
– первообразная от функции
(
)
[
]
xhx1
;
(
)
0
+
=
+
τ
xx
и
(
0−=
−
)
τ
xx
. Поскольку
, то сохраняет знак для всех . Значит,
()
0≠xh
()
xh
0>x
ϕ
– монотонная функция с
особенностью в нуле. Из соображений непрерывности положим при
0=
+
x 0
=
−
x .
Из соотношения (1.4) значение определяется единственным образом и, более
того, является некоторой гладкой функцией от .
+
x
+
x
−
x
Для примера рассмотрим модель (1.1) в форме Контуа
)]Kx1/()t(1[xx
+
+
−
+
−=
τ
μδ
&
, (1.5)
где
μ
и K - неотрицательные константы. Величина
μ
характеризует
продуктивность, а параметр
τ
- момент размножения популяции. В точке скачка
”снизу -верх” t=
τ
получаем соотношение
μ
ϕ
ϕ
+
=
−+
)x()x( , (1.6)
где
x)xln()K1()x( ++=
ϕ
; x
+
=x(
τ
+0) и x
-
=x(
τ
-0). Из формулы (1.6) значение x
+
находится единственным образом. Неявная гладкая зависимость x
+
=S(x
-,
K)
оказывается возрастающей и вогнутой (=выпуклой вверх) функцией от , а по
−
x
K
данная функция убывает. Исходя из соображений непрерывности, положим x
+
=0
при x
-
=0.
Теперь легко построить отображение Пуанкаре для модели (1. 5). Здесь
удобно выбрать следующие обозначения y
m
=x(mT+
τ
+0) для целых m. В открытом
интервале (mT+
τ
+0, mT+T+
τ
-0) переменная x экспонентциально убывает и с
учетом формулы (1.6) получаем рекуррентную последовательность
66
ϕ
(y
m+1
)=
ϕ
(y
m
)+
T[
μ
/T-
1-
K-
y
m
/r], (1.7)
где
ϕ
(z)=(1+K) ln(z)+z; 1/r=[1-exp(-T)]/T. Рекурсия (1.7) задает возрастающую и
выпуклую вверх функцию y
m+1
=g(y
m
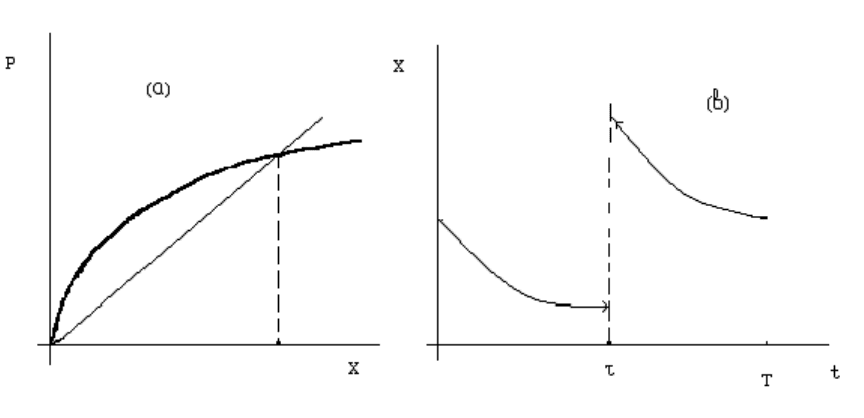
) с начальным условием g(0)=0 (рис.3.1а).
Рис. 3.1. Отображение Пуанкаре для уравнения (1.5) – (а). Поведение переменных
в D – системе – (в).
При
μ
/T>1+K существует y
*
- положительная неподвижная точка
отображения g . Очевидно, равновесие y
*
глобально устойчиво в R
+
.
Приведенный пример допускает распространение и на динамику
конкурентного сообщества. Данные модели, так называемые D – системы,
обладают примечательным свойством: их периодические режимы могут быть
найдены как решения некоторой системы линейных алгебраических уравнений.
Для иллюстрации рассмотрим случай двух конкурентов:
)]1/()(1[
211111
xxtxx
+
+
−
+−=
τ
δ
μ
&
, (1.8)
)]1/()(1[
212222
xxtxx
+
+
−
+−=
τ
δ
μ
&
,
где
μ
i
> 0 для всех i; 0 <
τ
1
<
τ
2
<T;
δ
является
T
-
периодической дельта -
функцией. Каждая переменная x
i
в модели (1.8) на временном отрезке [0,T]
является убывающей экспонентой, за исключением "своей" точки
τ
i
, в которой
имеет место скачок (рис. 3.1б). В точке
τ
i
значение x
i
(
τ
i
) не определено, однако
существуют пределы слева x
i
(
τ
i
-0) и справа x
i
(
τ
i
+0). Условие
τ
1
≠τ
2
позволяет
избежать трудностей, связанных с неоднозначностью величины x
i
в точке t=
τ
i
. Так,
67
в уравнении для x
1
важно лишь значение переменной x
2
в малой окрестности точки
t =
τ
1
, в которой x
2
непрерывна и, значит, однозначно определена. В целом, роль
дельта - функций сводится к тому, что "нелинейности" проявляются лишь в
"бесконечно малые" интервалы времени.
Для всех i положим =x
i
(mT+
τ
i
+0),
и пусть заданы величины .
Предложенный выше порядок чередования скачков {
τ
i
} задает естественную
последовательность вычислений y - переменных: сначала вычисляем , потом
вычисляем , затем все вновь повторяется.
m
i
y },{
21
mm
yy
1
1
+m
y
1
2
+m
y
Более конкретно, обозначим
b
12
=exp(
τ
2
-
τ
1
- T) и b
21
=exp(
τ
1
-
τ
2
).
Теперь, используя соотношение (1.7) при K
1
=b
12
, получаем
m
y
2
ϕ
1
( )=
ϕ
1
( ) + TL
1
( ),
1
1
+m
y
m
y
1
mm
yy
21
,
где
ϕ
1
(z)=(1 + K
1
) ln(z) + z
- нелинейная функция;
L
1
=
μ
1
/T - 1 - /r – b
12
- линейная форма; 1/r=[1-exp(-T)]/T.
m
y
1
m
y
2
Аналогично, для переменной y
2
при K
2
=b
21
устанавливаем
1
1
+m
y
ϕ
2
( )=
ϕ
2
( ) + TL
2
( ),
1
2
+m
y
m
y
2
mm
yy
2
1
1
,
+
где
ϕ
2
(z)=(1 + K
2
) ln(z) + z
и L
2
=
μ
2
/T - 1 - /r – b
21
.
m
y
2
1
1
+m
y
В дальнейшем считаем, что
T
i
>
μ
. В противном случае
i
- тая популяция
вымирает сама по себе.
Каждое из рекурентных уравнений задает “свою” гладкую функцию
),(
211
1
1
mmm
yygy =
+
и .
),(
2
1
12
1
2
mmm
yygy
++
=
При этом функция g
i
вогнута и возрастает по "своей" переменной y
i
, но убывает по
"чужой" переменной . Данные соотношения определяют отображение
i3
y
−
P
: ( , )
→
( , ),
m
1
y
m
2
y
1m
1
y
+ 1m
2
y
+
которое расщепляется в композицию простых (изменяющих лишь одну
координату) отображений:
1
Q : ( , )
→
( , ) и : ( , )
→
( , ).
m
1
y
m
2
y
1m
1
y
+ m
2
y
2
Q
1m
1
y
+ m
2
y
1m
1
y
+ 1m
2
y
+
Возможность такого расщепления существенно облегчает исследование динамики
дискретной D – системы.
