Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.


28
положительный коэффициент мутаций; биомасса водорослей измеряется в
единицах фосфора. «Близость» популяций заключается в равенстве скоростей
смертности и роста, а также возможности обмена (мутаций) между популяциями. А
единственное отличие состоит в разных временах распада отмерших водорослей.
В данной системе имеется следующий линейный инвариант
() () () () ()
∫∫
−−
≡+α++α+
t
at
t
at
Ctydssxtxdssxtx
12
2211
,
соответствующий закону сохранения фосфора в (4.1). Здесь для определения
положительного равновесия следует задать общее количество фосфора в
системе. Тогда для нахождения координат положительного равновесия
()
C
(
)
**
2
*
1
,, yxx
получаем три условия:
,
()()
0,,
*
1
*
2
**
2
*
1
*
1
=−++− xxmyxxRx
βα
(
)( )
0,,
*
2
*
1
**
1
*
2
*
2
=−++− xxmyxxRx
βα
,
(
)
(
)
Cyaxax =+α++α+
*
2
*
21
*
1
11
.
Из этих уравнений однозначно находятся координаты. Обоснование
локальной устойчивости данного равновесия опирается на критерии устойчивости
двухконтурных систем (см. раздел 1.2). Более того, компьютерный анализ
позволяет выдвинуть следующую гипотезу:
если положительное равновесие в
модели (4.1) локально устойчиво, то оно и глобально устойчиво.
Отметим, что здесь фитоценоз, представленный только одной из популяций
оказывается неустойчивым, если каждое
а
i
больше критического. Следовательно,
конкурентное взаимодействие двух «неустойчивых» популяций водорослей может
привести к стабилизации их динамики.
2. Стабилизирующее действие хищничества. Рассмотрим модель «фосфор
– фитопланктон
(
– зоопланктон
()
y
)
x
(
)
z
»:
() ()
.
,,
2
2211
12
2
1
1
yx
xy
atxatzy
kzx
zx
yx
xy
xx
kzx
zx
zz
+
−−+−=
+
−
+
+−=
+
+−=
β
αα
ββ
α
β
α
&
&
&
(4.2)
Здесь взаимодействие z
x
↔ также представлено в форме Контуа.
В данной системе имеется линейный инвариант

29
() () () () ()
Ctydssxtxdssztz
t
at
t
at
≡+α++α+
∫∫
−−
21
21
,
соответствующий закону сохранения фосфора. Координаты положительного
равновесия
(
)
***
,, yxz
модели (5.2) удовлетворяют системе:
()( )
.11
,0,0
*
22
*
11
*
**
**
1
**
**
2
*
2
**
**
1
*
1
Cyaxaz
kzx
xz
yx
yx
x
kzx
xz
z
≡++++
=
+
−
+
+−=
+
+−
αα
ββ
α
β
α
Положим
iii
α
−
β=
γ
для . При
2,1=i
0
1
>
γ
, 0
2
>
γ
и
k
12
γ
>
γ
здесь существует
единственное положительное равновесие.
При отсутствии хищника
(
)
0
≡
z
система «фитопланктон – фосфор»
описывается одноконтурной моделью. Согласно разделу 1.2 при большом
(например,
2
a
17
2
=
a ) положительное равновесие данной усеченной модели
неустойчиво. Напротив, в полной модели действуют две обратные связи, и при
определенных условиях возникает локальная устойчивость равновесия. Более того,
при конкретной реализации таких условиях (в частности, , ,
13=k 1
1
=α 12
1
=
β
,
, и ,
3
2
=α 4
2
=β 10
1
=a 17
2
=
a ) на основе компьютерных экспериментов
установлена глобальная устойчивость равновесия (4. 2).
В целом, уменьшение численности хищника – зоопланктона (или его полное
уничтожение) может дестабилизировать систему «фосфор – фитопланктон –
зоопланктон».
3. Дестабилизация при эвтрофировании. Рассмотрим систему «водоросли
– фосфор и азот ». Поскольку азот и фосфор в математическом смысле
равноправны, то биомассу водорослей будем измерять в абсолютных единицах – в
сыром весе. Для учета баланса элементов введем два параметра ,
–
содержание фосфора и азота в клетках водорослей. Тогда соответствующая модель
принимает вид (Ильичев, 1988а):
()
x
()
y
()
z
P
k
N
k
(
)
()( )
[]
()()
[
,,,,,,
,,,
21 NP
kzyxRatxzkzyxRatxy
zyxRxx
βαβα
βα
−−=−−=
+−=
&
&
&
]
(4.3)
где
()
()
PN
zkykxyz
xyz
zyxR
++
=,,
1
a, – время распада отмерших водорослей до

30
минерального фосфора; – время распада до минерального азота (например,
аммония). Известно (Сергеев, 1979), что существенно меньше .
2
a
1`
a
2
a
Разумеется, в (4.3) представлен один из возможных вариантов зависимости
скорости роста водорослей от двух факторов питания (азота и фосфора). Отметим,
что здесь при неограниченном увеличении, например, азота определяющим
(лимитирующим) фактором динамики фитопланктона является только фосфор. Это
обстоятельство, действительно, реализуется в модели (4.3), поскольку при
∞
→z
возникает прежняя однофакторная зависимость Контуа
()
pPN
xky
xy
zkykxyz
xyz
+
β
→
++
β
.
Далее, модель (4.3) имеет два аддитивных первых интеграла, выражающих
соответственно баланс фосфора
(
)
P
C и азота
(
)
N
C :
() () ()
PP
t
at
Ckdssxtxty ≡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
++
∫
−
1
α
, .
() () ()
NN
t
at
Ckdssxtxtz ≡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
++
∫
−
2
α
Отсюда сразу следует: соответствующее характеристическое уравнение
будет иметь два нулевых корня, которые, однако, не влияют на характер
устойчивости равновесий (при возмущениях системы, не изменяющих запасы азота
и фосфора).
Пусть заданы общие запасы фосфора и азота в системе. Тогда
положительное равновесие определяется из следующего набора
уравнений:
),,(
***
zyx
(
)
() ()
.1,1
,0,,
2
**
1
**
****
NNPP
CkaxzCkaxy
zyxRx
=++=++
=+−
αα
βα
(4.4)
При поиске решений в алгебраической системе (4.4) удобно ввести новые
переменные
P
kx
y
*
*
=ζ и
N
kx
z
*
*
=ξ . Тогда получаем
β
α
=
ξ+ζ+ζξ
ζ
ξ
,
Q
a
a
=
α++ζ
α
+
+
ξ
1
2
1
1
(4.5)
где
PP
NN
kC
kC
Q
/
/
=
– отношение (приведенных) запасов биогенных веществ.
При
первое уравнение (4.5) представляет собой гиперболу в , а
α>β
2
+
R
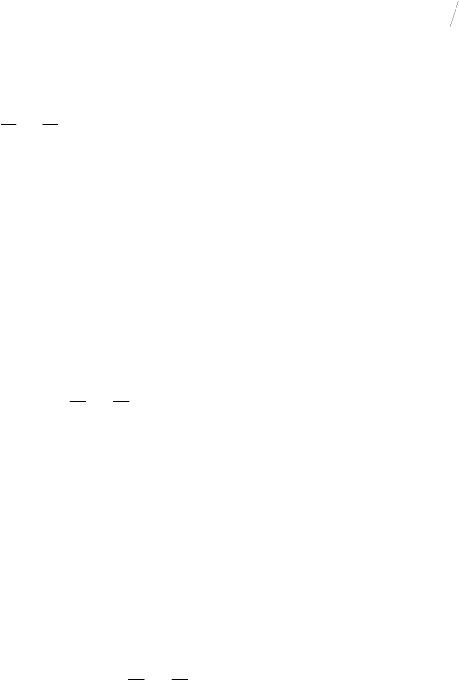
31
второе – прямую, которая составляет острый угол с осью абсцисс. Поэтому в (5.5)
существует единственное положительное решение. Данное решение
(
)
ξ
ζ
,
позволяет однозначно определить положительное равновесие в (4.4). Очевидно,
координаты равновесия и коэффициенты характеристического уравнения
находятся в зависимости от величины . Поэтому устойчивость данного
равновесия может определяться величиной Q. Для иллюстрации приведем
конкретный пример модели (4.3) с параметрами
Q
3
=
α
,
4=
β
, , 10
1
=a 17
2
=
a и
вариацией отношения
Q
.
Запасы азота и фосфора одного порядка. Пусть 1429=Q . Тогда
характеристическое уравнение можно преобразовать к виду
[]
)17exp()10exp(
4
3
4
3
2
μμμ
.
μ
−+−=++
Оно не имеет корней с
0Re >
μ
. Следовательно, равновесие модели (4.3) локально
и, как показали, компьютерные расчеты, глобально устойчиво.
Избыток азота. Пусть
∞
→Q
. Например, если С
P
–фиксировано, а
. Тогда характеристическое уравнение приобретает вид ∞→
N
C
)10exp(
4
3
4
3
2
μμμ
−=++
.
Оно имеет пару корней с
0Re >
μ
. Следовательно, теперь равновесие модели
неустойчиво.
Избыток фосфора. Пусть . Например, если С
N
-фиксировано, а
. Тогда характеристическое уравнение
преобразуется к виду
0→Q
∞→
P
C
),17exp(
4
3
4
3
2
μμμ
−=++
,
которое имеет две пары корней с
0Re >
μ
. Это означает, что и в данной ситуации
равновесие неустойчиво. Здесь в системе (4.3) реализуются колебания большей
амплитуды, чем в предыдущем случае.
В целом, если запасы азота и фосфора в водоеме сбалансированы (
и
одного порядка), то активно действуют две обратные связи (по азоту и фосфору) и
фитоценоз устойчив (рис. 1. 11 а) Напротив, избыточное накопление какого-либо
биогенного вещества ослабляет одну из двух обратных связей и может
N
C
P
C
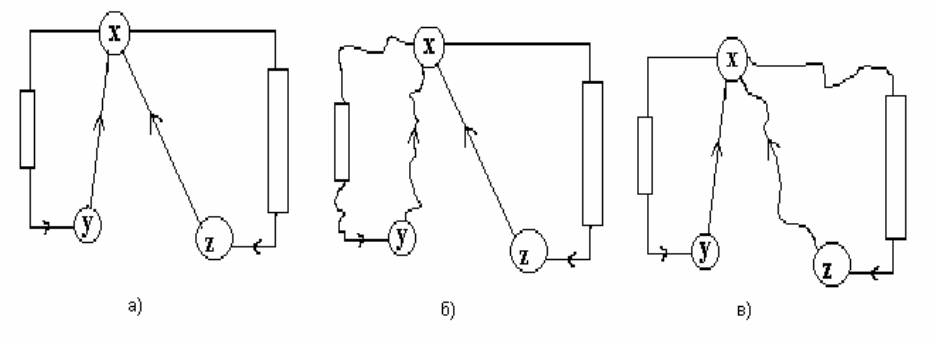
32
дестабилизировать фитоценоз. При этом увеличение количества фосфора в
экосистеме более «опасно» (рис. 1. 11 б), чем избыток азота (рис. 1. 11 в),
поскольку в первом случае возникают колебания большей амплитуды.
Рис. 1. 11.
Ослабление обратных связей в системе «водоросли – азот и фосфор».
Обсуждение.
В общем случае допустимые описания некоторого модельного процесса
могут составлять выпуклое (и компактное в каком-то смысле) множество. Тогда
эффективный план исследования “от простого к сложному” опирается на теорему
Крейна -Мильмана (Фелпс, 1968):
всякая точка выпуклого компакта является
выпуклой комбинацией его крайних точек (=вершин).
На первом этапе необходимо
выделить базисные процессы – крайние точки, и затем изучать поведение
соответствующих моделей. На втором и следующих этапах можно усложнять
структуру процесса путем образования выпуклых комбинаций из базисных.
Зачастую, уже реализация первого этапа доставляет много ценной информации
(см. главу 3).
В качестве другого примера рассмотрим дискретную модель миграции
рыбной популяции. Пусть акватория разбита на районов и -
текущий вектор численности популяции по районам. Преобразование
является композицией двух процессов: нелинейного (
F
), ответственного за
размножение - гибель, и неотрицательной матрицы (
n
),...,(
1 n
xxX =
1+
→
tt
XX
M
), осуществляющая
“перемешивание” популяций между районами. Формально, имеет место
.
)(
1 tt
MXFX =
+
33
Далее, поскольку перемешивание не изменяет общей численности, то сумма
элементов в каждом столбце равна 1. Данное семейство матриц представляет собой
выпуклый многогранник (
K
) в - мерном пространстве. Вершинами
2
n
K
являются
матрицы, у которых в каждом столбце находится одна 1, а остальные элементы
равны 0 (Ильичев, 2007а). Поэтому теоретический анализ таких моделей
целесообразно начинать с базисных матриц
M
.
1.5. Приложение. Обоснование основных результатов
Анализ устойчивости уравнения (2.2). Метод D-разбиений основан на
непрерывной зависимости положения корней (квазимногочленов) от его
коэффициентов. Когда эти коэффициенты находятся на границе, разделяющей
области устойчивости и неустойчивости, то уравнение с необходимостью
содержит чисто мнимый корень. Так как коэффициенты квазимногочленов
вещественные числа, то мнимые корни представлены комплексно-сопряженными
парами
iy±=
μ
. Поэтому ниже будем считать .
0≥y
Итак, подставим мнимый корень
iy
=
μ
в (2.2). Тогда, выделяя
вещественную и мнимую части, получаем соотношения:
).sin(
),cos(
2
yay
yay
εγ=−
εγ=−ε
(П.1)
Следуя (Ильичев, Ильичева, 1998б), изложим основные результаты исследования.
Неравенство – необходимое условие совместности системы (П.1).
Зафиксируем такое
4/3
2
≥γ
γ
и выразим параметры
ε
, через
a
y
. С учетом условий
1
≤
ε
и получаем однозначное решение
()
0sin ≤ay
w
)w(1
2/12
−−
=
γ
ε
и
y
)]/()y[(arccosk2
a
2
εγεπ
−−
=
, (П.2)
где и - натуральное число. При заданном и вариации в
диапазоне
22
y/)1(w
γ
−=
k k
y
75.05.0y
22
−≤−
γ
уравнения (П.2) задают некоторую кривую –
границу “лакуны”. Показано, что когда точка
)a,(
ε
перемещается от границы во
внутрь лакуны, тогда соответствующий мнимый корень (2.2) переходит в правую
комплексную полуплоскость. В целом, уравнение (2.2) неустойчиво, если и только
если точка
)a,(
ε
находится внутри какой-либо лакуны.

34
Доказательство утверждения 1.1. Подставим корень
iy=
μ
при .в
(2.4) при
0y ≥
1=
ε
и 2/1
21
=
=
λ
λ
. . После выделения мнимой и вещественной
частей получаем:
(
)
(
)
() ()
.2/]sin[sin
,2/]cos[cos1
21
21
2
yayay
yayay
+=−
+=−
γ
γ
(П.3)
Выясним при каких
γ
данная система совместна. После возведения в квадрат и
складывания уравнений (П.3) получаем:
. (П.4)
242
yy1
γ
≤+−
Отсюда вытекает
75.05.0y
22
−≤−
γ
. Поэтому для совместности (П.3) должно
выполняться необходимое условие . Справедлива
75.0
2
≥
γ
Лемма.П.1.
При квазимногочлен (2.4) не имеет плохих корней.
75.0
2
<
γ
В самом деле, положим
1)(f
2
++=
μμμ
и
2/)]exp()[exp()(
21
μ
μ
γ
μ
aag −
+
−
=
.
Легко убедится, что на границе правого полукруга
{
}
велико,,0Re| −≤≥=
+
RRD
R
μμμ
выполняется неравенство
)(g)(f
μ
μ
>
. Отсюда согласно теореме Руше
(Гурвиц, 1933) функции
)(f
μ
и
)(g)(f
μ
μ
−
имеют одинаковое количество
корней в . Функция
+
R
D
)(f
μ
не имеет корней в при любом
+
R
D
R
. И значит,
уравнение (2.4) не имеет плохих корней. Лемма П.1. доказана.
Для система (П.3) разрешима относительно переменных и
двумя способами. При этом имеют место соотношения ( и
– натуральные):
4/3
2
≥
γ
1
a
2
a
1
k
2
k
)(2)(2)(
12121
yJkkaay
−
+=+
π
, (П.5)
)(2)(2)(
22121
yJkkaay
±
−=−
π
.
Здесь
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−
−
=
42
2
1
1
1
arccos
yy
y
yJ
и
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−
=
γ
γ
42
2
1
arccos,
yy
yJ
.
Пусть заданы и , а переменная варьирует в диапазоне
1
k
2
k
y
75.05.0y
22
−≤−
γ
.
Тогда с помощью формул (П.5) каждый из двух вариантов задает свою кривую в

35
пространстве . Если переменная совпадает с одним из двух концов своего
диапазона, то эти кривые пересекаются. Так, для каждой граничной точки
имеем:
),(
21
aa
y
*
y
и . (П.6)
**
11
*
1
/)](2[ yyJka −=
π
**
12
*
2
/)](2[ yyJka −=
π
В совокупности указанные кривые ограничивают “остров”
),,(
21
γ
kkUn
.
Согласно формулам (П.5) при возрастании параметра
γ
размер каждого острова, в
целом, увеличивается. Для дальнейшего удобно представлять себе следующее
трехпараметрическое пространство: вертикальная ось соответствует
γ
, а в
горизонтальной плоскости находятся координаты . При фиксированных
, объединение
),(
21
aa
1
k
2
k ),,(
21
γ
kkUn
для всех
γ
от 2/3 до 1 оказывается конической
поверхностью (см. рис. 1.12). Поскольку точка принадлежит конической
поверхности, то существует мнимый корень . Обсудим его “судьбу” при
увеличении
)a,a,(
*
2
*
1
γ
iy
γ
. Для этого продифференцируем уравнение (2.4) по параметру
γ
:
∑
∑
==
−=−++
2
1
2
1
)exp(])exp(24[
j
j
j
jj
aaaD
μμγμμ
,
где
γ
μ
μ
∂∂= /D
. Подставляя сюда и из (П.6), устанавливаем
*
iy=
μ
)a,a(
*
2
*
1
0)Re( >
μ
&
. Поэтому внутренние точки конуса – это область неустойчивости
уравнения (2.4).
Обозначим через
Σ
- множество всех точек, находящихся вне всех конусов.
Если из такой точки опустить вертикальный отрезок, то он не пересечет ни одного
конуса. Поэтому внутри
Σ
любые две точки можно соединить - образной
ломанной с основанием
U
2/3<
γ
. Значит,
Σ
- связное множество, и согласно
доказанной выше лемме
Σ
- область устойчивости уравнения (2.4).
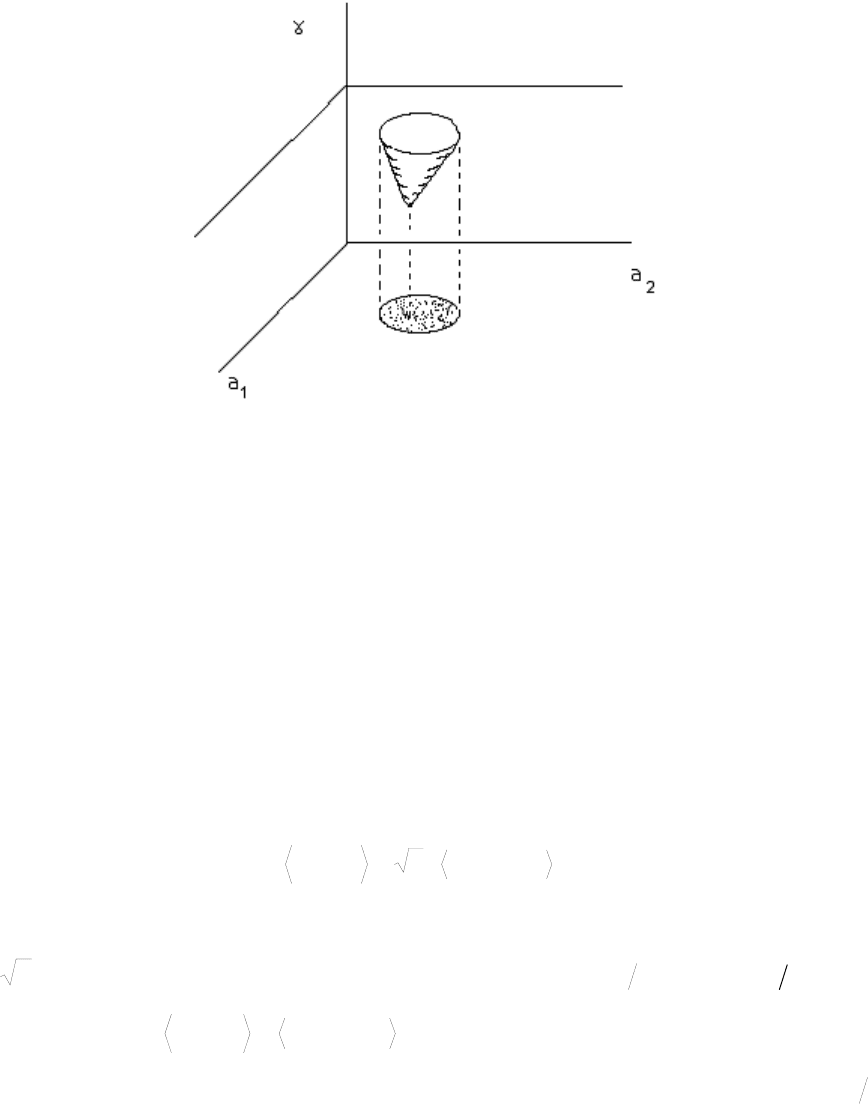
36
Рис. 1. 12.
К анализу параметрического портрета уравнения (2.4).
Доказательство утверждения 1.2. Достаточно показать, что
иррациональная прямая может сколь угодно близко подходить к центрам
некоторых полуостровов. А поскольку центр является серединой отрезка
фиксированной длины (принадлежащего полуострову), то обязательно возникнет
пересечение данной прямой и указанных полуостровов. Сделаем замену
переменных и
2/)(
21
aas += 2/)(
12
aar
−
=
. Теперь координаты центра задаются
выражением
mnrs
mn
,3.02,
**
−=
π
,
где – целые и ,
mn,
1≥n
nmn
≤
≤
− . Данные центры образуют решетку с шагом
π= 2h
. Удобно перейти к другим переменным hSS
nn
=
и hrR
mm
= . Тогда
«новые» центры
mnRS
mn
,3.0,
**
−= образуют решетку с единичным шагом.
Каждый такой центр находится в середине вертикального отрезка длины
nm
I 31 ,
принадлежащего полуострову.
Пусть задана прямая
β
+
α
=
SR
с иррациональным . Построим
последовательность
α
(
)
βαξ
+=
*
nn
SFr
,
где – дробная часть числа. Согласно учебнику Арнольда (1984)
последовательность
{
всюду плотно заполняет отрезок
()
KFr
}
n
ξ
[
]
1,0 . В частности, когда
n
ξ
оказывается меньше 1/6 или больше 5/6 , тогда точка

37
>+<
βα
**
,
nn
SS
будет принадлежать отрезку при некотором
m . Значит, возникает пересечение
данной прямой с некоторым полуостровом.
nm
I
Доказательство утверждения 1.3. Сначала выведем некоторые
необходимые условия, характеризующие устойчивые направления. Пусть прямая
не пересекает границу (как верхнюю, так и нижнюю) полуострова
. Тогда из формул (П.5) следует, что должны одновременно выполняться
соотношения:
β=−
2112
nana
(
21
,kkUn
)
(
)
(
)
2112
2 nknkyq
−
π
≠
(П.7)
для всех из при
y
(
]
1,0
()
(
)
(
)
(
)
(
)
yJnnyJnnyyq
221121
+
−
−
+
β
= ;
(
)
(
)
2112
2 nknkyp
−
π
≠
(П.8)
для всех из при
y
(
]
1,0
()
(
)
(
)
(
)
(
)
yJnnyJnnyyp
221121
+
+
−
+
β
= .
При фиксированных и отметим полезные свойства непрерывных
функций и на отрезке
1
n
2
n
()
yq
()
yp
(
]
1,0
. Так данные функции совпадают в начальной
точке
() ()
000
=
= qp
и конечной точке
() () ( )
2
11
21
π
−+β== nnqp
. Очевидно, для
остальных
y
из
(
)
1,0
выполняется неравенство
(
)
(
)
ypyq
<
.
Пусть данная прямая не пересекает границы ни одного полуострова, тогда
соотношения (П.7) и (П.8) имеют место для всех и . Рассмотрим, в
частности, следующие варианты выбора и :
1
1
≥k 1
2
≥k
1
k
2
k
1) при
21
nk
=
и
12
nk = получаем в правой части соотношений (П.7) и (П.8)
нули. Значит, функции
()
yq
и
(
)
yp
не имеют нулей на
(
]
1,0
. Далее, если
()
0
2
2
>
π
, тогда с учетом совпадения на краях и отсутствия нулей
заключаем, что графики обеих функций
1
−+β nn
p
и
q
лежат выше оси абсцисс.
Аналогично, при
()
0
2
21
<
π
−+β nn обе функции лежат ниже оси абсцисс. В
силу непрерывности и
()
yq
(
)
yp
от параметра
β
, заключаем, что и при
()
0
2
21
=
π
−+β nn обе данные функции должны быть или одновременно
положительны или одновременно отрицательны в промежутке ;
(
]
1,0
