Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.

68
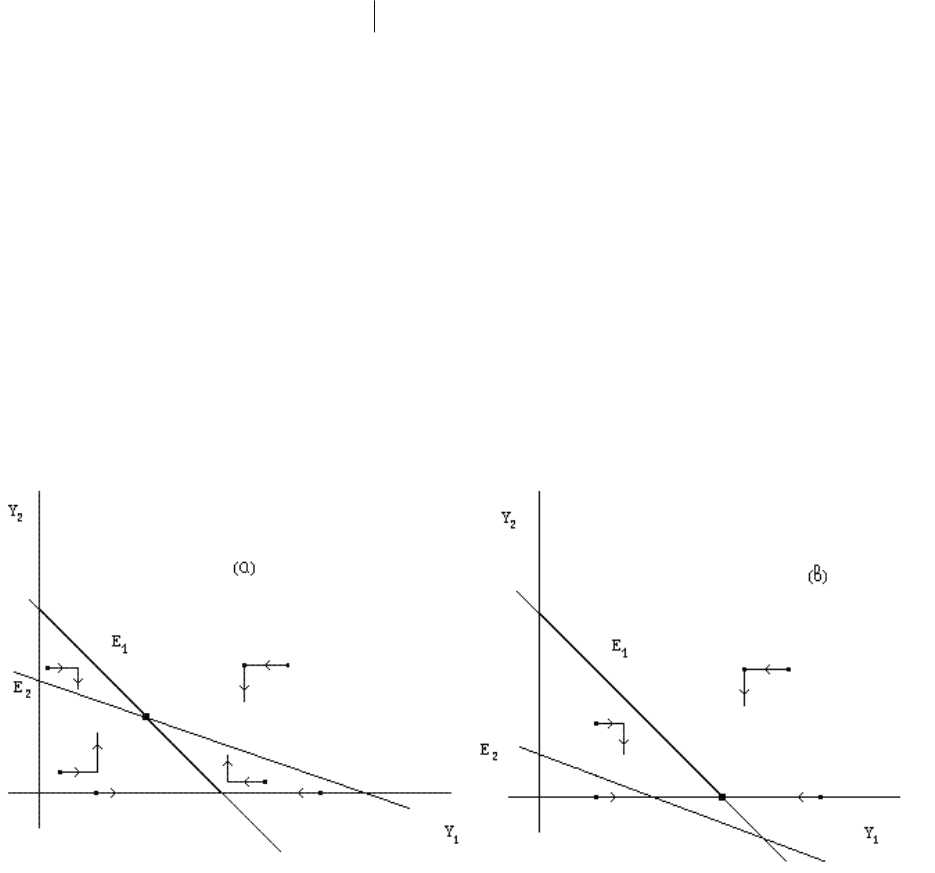
При анализе поведения важную роль играет взаимное расположение так
называемых изоклин и . Каждая изоклина определяется в соотношением
1
E
2
E
2
R
+
)}y,y(gy)y,y{(E
21ii21i
=
=
,
2,1i = . Очевидно, является куском прямой и задается уравнением (см. рис.3.2)
i
E
0)y,y(L
21i
=
.
Обозначим точки пересечения со своей (
i
- той) осью координатой ( ) и с
чужой - в точке ( ). Отрезок назовем основанием, а - высотой
- той изоклины. Оказывается, действие отображения
i
E
i
B
i
H ]B,0[
i
]H,0[
i
i
P
на фазовую точку
напоминает движение шахматной ладьи: сначала происходит ее горизонтальное
притяжение к , а затем ее вертикальное притяжение к . Притяжение является
”мягким”, поскольку фазовая точка не перескакивает соответствующих изоклин.
1
E
2
E
Рис. 3.2. Исход конкуренции в зависимости от расположения изоклин.
Далее, если в дискретной D - системе имеется положительное равновесие, то
его координаты удовлетворяют набору линейных алгебраических уравнений. Так, в
двумерном случае для равновесия ( ) из получаем:
*
2
*
1
y,y
2
R
+
/r
+ b
12
=
μ
1
/T-1, (1.9)
*
1
y
*
2
y
b
21
+ /r =
μ
2
/T-1 .
*
1
y
*
2
y
Здесь определитель
Δ
=1/r
2
- exp(-T) всегда больше нуля, поэтому данная система
однозначно разрешима. Положительное решение в системе (1.9) возникает тогда,

69
когда изоклины пересекаются в . При этом основание одной изоклины всегда
меньше высоты другой. Из рис. 3.2а сразу вытекает
2
R
+
Утверждение 3.1. Пусть в cистеме (1.9) существует положительное
равновесие, тогда оно глобально устойчиво в .
2
R
+
В этом случае в соответствующей модели (1.8) существует положительный,
T-периодический режим. Разумеется, верно и обратное. Поэтому в двумерной -
системе (1.8) существует не более одного такого режима.
D
Напротив, если в системе (1.9) получено , тогда в соответствующей
дифференциальной системе (1.8) имеет место
0
*
<
i
y
(
)
0→tx
i
при
∞→
t
.
В системе (1.9) обнаружены более или менее ”парадоксальные” явления.
Так, при
3=
T
имеют место:
1. Низкопродуктивная популяция может вытеснять высокопродуктивную.
Положим , ,
01.0
1
=τ 99.2
2
=τ 3
1
=
λ
, 9.2
2
=
λ
. Теперь из (1.9) находим
и
. Значит, менее продуктивная (вторая) популяция может вытеснять более
продуктивную (первую) популяцию.
0
*
1
<y
0
*
2
>y
2. Нетранзитивность вытеснения. Рассмотрим набор из трех популяций с
параметрами
21
1
=
τ , 23
2
=τ , 25
3
=
τ
и
6
321
=
λ
=
λ
=
λ
. Тогда, подставляя в
(1.9), параметры любых двух из названных популяций, убеждаемся: в двухвидовом
сообществе одна из популяций вытесняет другую. Более формально, обозначим
через
отношение: -тая популяция вытесняет
ji
xx f
i
j
-тую. В данном случае
имеем
3221
, xxxx ff и .
13
xx f
В рамках трехмерной D-системы Контуа обнаружено, что в сообществе из
трех указанных популяций устанавливается устойчивый,
T
-периодический режим.
Однако в некоторых других моделях "нетранзитивность" порождает сложный
режим, заключающийся в циклической смене доминирующих форм.
3. Нетранзитивность сосуществования. Обозначим через
отношение - тая популяция сосуществует с
ji
xx ~
i
j
-той. Возникает вопрос: пусть
и , тогда ? Оказывается это неверно. Так, при
21
~ xx
32
~ xx
31
~ xx 01.0
1
=
τ
,
34
2
=τ , 38
3
=τ и 6
321
=
λ
=λ=λ из анализа системы (1.9), получаем

70
21
~ xx и , но вытесняет .
32
~ xx
3
x
1
x
В общем случае динамика конкурентов в D – системе имеет вид
)]x...x1/()t(1[xx
n1iiii
+
+
+
−
+−=
τ
δ
μ
&
, (1.10)
где ; 0 <
τ
1
<…<
τ
n
<T; n,...,1i = T
i
>
μ
.
Положим ,
тогда аналогично предыдущему построим
соотношения, задающие динамику вектора
(
0+τ+=
ii
m
i
mTxy
)
{
}
mm
n
m
Yyy =,,
1
K
. Обозначим через
- вектор с компонентами
(
n
λλ=Λ ,,
1
K
)
1T/
ii
−
=
μ
λ
, и “матрицу
взаимодействий”
(
)
ijn
bB =
с элементами
(
)
()
⎪
⎩
⎪
⎨
⎧
τ=τ
τ<τ−τ−τ
τ>ττ−τ
=
.если,0
,если,exp
,если,exp
ji
jiij
jiij
ij
Tb
Так, при и равномерном расположении точек
3=n
{
}
i
τ
на
[
]
T,0 получаем
(
)
(
)
() ()
()()
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
−−
−−
=
03exp32exp
32exp03exp
3exp32exp0
3
TT
TT
TT
B
.
Обозначим через – суммарную численность остальных популяций в
момент времени . Нетрудно установить соотношение
m
k
c
k
TmT τ++
∑∑
+=
−
=
+
+=
n
kj
m
jkj
k
j
m
jkj
m
k
ybybc
1
1
1
1
;
В этом случае дискретная D –система приобретает вид:
(
)
(
)
(
)
m
n
m
k
m
k
m
k
m
kk
m
kk
yyyyTLyy ,,,,,
1
1
1
1
1
KK
+
−
++
+ϕ=ϕ
. (1.11)
()
z
k
ϕ – нелинейная функция, равная
(
)
zzc
m
k
++ ln1
;
k
L – линейная форма, равная .
m
k
m
kk
cry −− /
λ
Уравнение (1.11) также неявно задает гладкую функцию
(
)
m
n
m
k
m
k
m
k
m
k
yyyygy ,,,,,
1
1
1
1
1
KK
+
−
++
=
.
Поскольку при , то из соображений непрерывности
положим при для всех . Справедлива
0
1
→
+m
k
y 0→
m
k
y
0=
k
g 0=
k
y 1≥k
Лемма 3.1. Каждая функция возрастает и вогнута по "своей"
переменной и убывает по всем остальным – "чужим" переменным
i
g
i
y
()
ijy
j
≠
.

71
Если существует положительное равновесие
(
)
**
1
*
,,
n
yyY K=
, то его
координаты удовлетворяют линейной системе алгебраических уравнений
(
)
Λ=+
*
YBrE
n
, (1.11)
где
E
– единичная матрица и T/)]Texp(1[r1
−
−
=
. Приведем достаточное
условие устойчивости данного равновесия. Здесь весьма полезным оказывается
понятие продуктивной матрицы. Согласно монографии (Ицкович, 1976)
неотрицательная матрица называется продуктивной, если все её собственные
числа (по модулю) строго меньше единицы. Оказывается, условие продуктивности
матрицы не зависит от расположения точек
n
rB
{
}
i
τ
.
Утверждение 3.2. Матрица продуктивна, если и только если
выполняется неравенство
n
rB
(
)
(
)
(
)
rnnTnT 11expexp <
−
−
+
+
−
K .
Отметим, что матрица продуктивна при всех
2
rB
0>
T
. При
7.5≥
T
матрица
также является продуктивной. Пусть зафиксировано, тогда при достаточно
большом
3
rB
n
T
всякая матрица становится продуктивной.
n
rB
Пусть продуктивна, тогда у неё существует неотрицательный
собственный вектор с собственным значением . Поскольку
все недиагональные элементы положительны, то
n
rB
(
n
zzZ ,,
1
K=
)
10 <γ<
n
rB
Z
– строго положительный
вектор. В замыкании построим
n
R
+
ε
-параметрическое семейство вложенных кубов
() ( )
{
iiin
AyayyП
≤
≤
=ε ,,
1
K
для всех
}
ni ,,1 K
=
,
где
(
)
iii
zya ε−=
*
,0max
и ;
ε+=
iii
zyA
*
0≥
ε
. При возрастании это семейство
полностью заполняет , а при
ε
n
R
+
0→
ε
стягивается к равновесию. Обозначим через
наименьший куб, на границе которого находится . Легко видеть, что
(
m
П ε
)
0>
m
Y
()
},...,max{
*
1
1
*
1 nnn
m
m
zyyzyyY −−==
εε
.
Лемма 3.2. Пусть
0>
Y
и
(
)
YPY =
)
, тогда
(
)
(
)
YY
εε
<
)
.
Поскольку непрерывная неотрицательная функция
(
)
m
Y
ε
является строго
убывающей на орбите динамической системы (1.11), то сразу получаем
Утверждение 3.3.
Пусть в дискретной D-системе Контуа существует
72
положительное равновесие . Если матрица продуктивна, то точка
глобально устойчива в .
*
Y
n
rB
*
Y
n
R
+
Отсюда получаем классический результат Армстронга и Мак Гичи (1976) о
возможности устойчивого сосуществования любого числа конкурентов в
периодической среде (”парадокс 4”). А именно, при фиксированном n рассмотрим
D-систему Контуа с параметрами
(
)
nTi
i
1
−
=
τ
и T
n
>
=
=
λ
λ
K
1
. Здесь при любом
T
существует положительное равновесие. Когда
T
достаточно велико, то данное
равновесие является глобально устойчивым.
В связи с утверждением 3.3 возникает вопрос об устойчивости
положительного равновесия (если оно существует) в D-системе Контуа, когда
матрица непродуктивна. Приведем некоторые результаты компьютерных
экспериментов с дискретной системой (1.11). Так, при была обнаружена
неожиданная
n
rB
3=n
Гипотеза. Пусть в дискретной D – cистеме Контуа при существует
положительное равновесие, тогда оно глобально устойчиво в .
3=n
n
R
+
А при и непродуктивной матрице в D-системе Контуа происходит
"самоизреживание" сообщества конкурирующих популяций (некоторые
конкуренты вымирают). После этого для оставшихся популяций реализуется
устойчивое равновесие, при этом финальное состояние (набор выживших
популяций) зависит от выбора начального вектора .
3>n
n
rB
0
Y
Перейдем теперь к основной проблеме конкуренции – поиску достаточных
признаков отбора в периодически изменяющейся среде. В частности, найдем
условия, при которых первая популяция вытесняет другие. Для дальнейшего
полезно заметить, что данное отображение Пуанкаре
(
)
(
)
11
11
,,,,:
++
→
m
n
mm
n
m
yyyyP KK
естественно представить как композицию более простых отображений
. При этом
действует только на "свою" переменную , а
остальные переменные не изменяются. Положим для удобства
1
GGP
n
oKo=
i
G
i
y
(
)
(
)
(
)
niii
yygyYG ,,,,
1
KK
=
,
где и задается выражением (1.11). Здесь для сокращения в
()
n
yyY ,,
1
K=
i
g
73
функции оставлена только -тая переменная.
i
g
i
На фазовой плоскости определим множества (изоклины)
n
R
+
(
)
{
}
YYGYE
i
i
=
=
|
.
Ясно, что – гиперплоскость для каждого . Будем говорить: точка
лежит ниже , когда имеет место неравенство
i
E
i
(
n
yyY ,,
1
K=
)
i
E
ij
n
j
ijii
ybryYL
λ
<+=
∑
=1
)(
.
Очевидно, если
Y
лежит ниже , то под действием -тая координата данной
точки "движется вперед"
i
E
i
G
i
(
)(
iii
yyg >
)
. Аналогично, если точка
Y
лежит выше ,
тогда под действием она "движется назад"
i
E
i
G
(
)
(
)
iii
yyg
<
. Оказывается, данные
движения довольно "мягкие". Так, имеет место простая лемма о поглощении
Лемма 3.3. 1) Пусть
Y
лежит ниже , тогда и
i
E
(
)
YG
i
лежит ниже .
i
E
2) Если
Y
лежит выше , то и
i
E
(
)
YG
i
лежит выше .
i
E
Пусть
теперь ниже выполняется следующее соотношение запаса
(
)
[
]
TT
i
1exp
1
−
>
λ
λ
для всех . (1.12)
1>i
Отметим, что константа запаса
(
)
[
]
TTK 1exp
−
=
больше
1
при всех
0>
T
.
Геометрическая суть условия запаса заключается в следующем
Лемма 3.4. Пусть выполняется условие запаса, тогда гиперплоскость
лежит выше всех остальных гиперплоскостей
1
E
{
}
i
E .
При выполнении условии запаса первая часть леммы 3.3 может быть
усилена: если точка
Y
лежит ниже , то и точка
1
E
(
)
YG
i
лежит ниже для
каждого
i
.
1
E
Определим в замыкании следующую непрерывную неотрицательную
функцию (аналог функции Ляпунова):
n
R
+
()
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−λ=
∑
=
n
j
jj
ybryYL
2
111
,max
.
Очевидно,
()
0
=
YL
, если
и только если
(
)
0,,0,
1
K
λ
=
rY . Данную равновесную
точку (в которой первая популяция вытеснила остальные) обозначим через .
Далее, функция состоит из кусков аналитического представления
*
1
R
L
74
гиперплоскости
, поэтому величина
1
E
(
)
YL
во многом определяется положением
точки
Y
относительно .
1
E
В дальнейшем считаем, что все координаты начальной точки положительны
(тогда и соответствующая орбита принадлежит ).
n
R
+
Лемма 3.5.
При выполнении условия запаса функция не возрастает на
орбите дискретной системы Контуа. При этом
L
(
)
(
)(
YLYPPL <o
)
для
Y
из .
n
R
+
Из данной леммы сразу вытекает достаточный признак отбора
Утверждение 3.4. Пусть в D-системе Контуа выполняется условие запаса
(1.12). Тогда первая популяция вытесняет остальные.
Величину естественно назвать константой запаса в D-системе
Контуа. Неожиданно, она является универсальной для любого количества
популяций в сообществе.
TT /]1)[exp( −
3.2. DD – система Контуа.
”Плотные” эволюционно – устойчивые параметры роста популяций
Одной из важных характеристик экологических процессов является понятие
об эволюционно- устойчивых параметрах популяций, смысл которого заключается
в следующем (Абросов, Боголюбов, 1988). Предположим, что исходная популяция
с параметром находится в устойчивом равновесном динамическом
режиме (стационарном, периодическом и т. д.). Пусть в некоторый момент времени
порождает некоторое количество мутантов {
)(X
*
τ
*
τ
)(X
*
τ
)(X
1
τ
,..., )(X
n
τ
}, имеющих
малые начальные численности. Тогда значение называется эволюционно -
устойчивым (ЭУ - параметром), если популяция
не вытесняется в
сообществе { ,
*
τ
)(X
*
τ
)(X
*
τ
)(X
1
τ
,..., )(X
n
τ
} при любом наборе параметров
n1
,...,
τ
τ
сколь – угодно близких к . По сути, эволюционная устойчивость – это свойство
не проигрывать в конкурентной борьбе. Поэтому в процессе эволюции могут
реализоваться только эволюционно- устойчивые параметры.
*
τ
При исследовании проблем эволюционной устойчивости необходимо
заранее задать N - максимально возможное число мутантов у исходной популяции.
Чем больше N, тем "труднее" параметру оказаться эволюционно - устойчивым.
*
τ
75
Актуальна проблема геометрической структуры множества ЭУ - параметров.
Если данное множество является достаточно "массивным", тогда результат
действия процессов микроэволюции оказывается весьма неоднозначным.
Разумеется, решение данной задачи на основе только компьютерных
экспериментов невозможно, поскольку условие “сколь - угодно близко”
нереализуемо в рамках конечной разрядной сетки. Поэтому возникает
необходимость в разработке моделей конкуренции, которые допускают
эффективное исследование.
Рассмотрим модификацию D - систем Контуа (т. н. DD - системы), в которой
каждый конкурент имеет на [0,2T] "свои" две (симметричные относительно T)
точки роста, а именно:
τ
и
τ
)
=2T-
τ
. В этой связи, зададим скорость роста в форме
β
(t,
τ
) =
μδ
(t-
τ
) +
μδ
(t-
τ
)
),
где 0 <
τ
<T; δ является 2T-периодической дельта - функцией.
Пусть
μ
=
μ
(
τ
) - гладкая функция для всех
τ
из [0,T]. Здесь возникает
следующая “частная” проблема:
существуют ли эволюционно – устойчивые параметры
τ
,
если допускается возникновение лишь одного мутанта ?
В этой связи, рассмотрим взаимодействие двух конкурентов:
1
= w
1
[-1 +
β
(t,
τ
1
)/(1 + w
1
+ w
2
) ], (2.1)
w
&
2
= w
2
[-1 +
β
(t,
τ
2
)/(1 + w
1
+ w
2
) ],
w
&
где 0 <
τ
1
<
τ
2
<T;
β
(t,
τ
i
) =
μ
(
τ
i
) [
δ
(t-
τ
i
) +
δ
(t-
τ
)
i
) ] для i=1,2.
Отметим, что на временном отрезке [0,T] рост первой популяции
происходит раньше второй, а на отрезке [T, 2T] наоборот. Такая ситуация
наблюдается в водных экосистемах: в первой половине года (весна+лето/2)
первыми размножаются холоднолюбивые водоросли, зато во второй половине года
(лето/2+осень) - теплолюбивые водоросли.
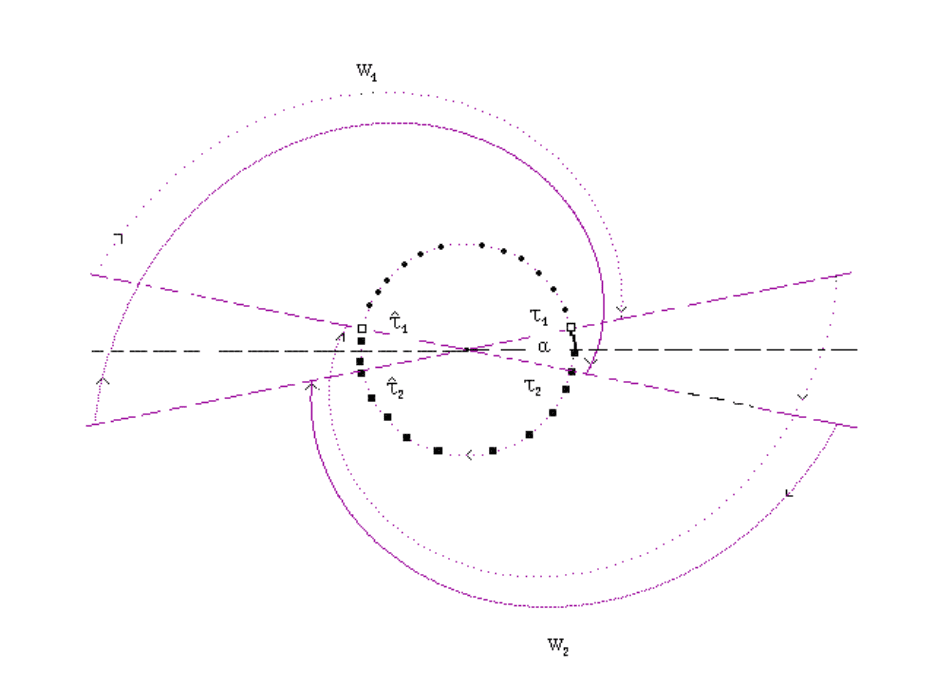
Введем промежуточную точку (
α
) из условия
τ
1
<
α
<
τ
2
. В дальнейшем
будем предполагать, что при деформации параметров
τ
1
,
α
,
τ
2
выполняется
следующее условие (допустимые параметры):
τ
1
<
α
<
τ
2
.
На циклической шкале времени (окружность длины 2T, обходимая по
часовой стрелке) выделим два интервала (нижний и верхний):
76
I
н
=[2Tn+
α
, 2Tn+2T-
α
] и I
в
=[2Tn+2T-
α
, 2Tn+2T+
α
].
Все точки роста первого конкурента расположены в I
в
, а второго - в I
н
. Это
обстоятельство - "разделение переменных" - существенно упрощает дальнейшее
исследование. Так, пусть заданы x
0
=w
1
(
α
) и y
0
=w
2
(2T-
α
). Построим отображение
x
0
→
x
1
=w
1
(
α
+2T).
Рис. 3.3. Удобное разбиение циклической шкалы времени на участки.
Удобно представить интервал [
α
,
α
+2T] в виде объединения пяти промежутков
{I
1
,…, I
5
} (рис. 3.3). На каждом I
m
построим “свое” сдвиг-отображение
π
m
:
1) на I
1
=[
α
, 2T-
τ
1
) переменная w
1
экспонентциально убывает, поэтому
π
1
:
x
→
x exp(
α
+
τ
1
-2T);
2) в I
2
=точке [2T-
1
τ
] происходит скачок переменной w
1
, который
описывается функцией S (см. раздел 3.1)
π
2
:
x
→
S(x, k
1
),
где k
1
=w
2
(2T-
τ
1
)=y
0
exp (
τ
1
-
α
);
3) на I
3
=(2T-
τ
1
, 2T+
τ
1
) переменная w
1
экспонентциально убывает, поэтому
77
π
3
:
x
→
x exp(-2
τ
1
);
4)
в I
4
=точке [2T+
τ
1
] происходит скачок переменной w
1
, поэтому
π
:
x
→
S(x, k
2
),
4
где k
2
=w
2
(2T+
τ
1
)= y
0
exp(-
τ
1
-
α
);
5) на I
5
=(2T+
τ
1
, 2T+
α
] переменная w
1
экспонентциально убывает, поэтому
π
5
:
x
→
x exp(
τ
1
-
α
).
Отображение Q
1
: x
0
→
x
1
является композицией отображений {
π
5
,...,
π
1
},
каждое из которых оказывается строго возрастающей и вогнутой функцией x.
Поэтому и Q
1
оказывается такой же функцией ;
0
x
0)0(Q
1
=
.
Ясно, что x
1
непрерывно дифференцируемая функция от допустимых
параметров
τ
1
,
τ
2
,
α
.
Приведем две полезные формулы для . Так, получаем
1
Q
]T2)y(Iexp[x/)y,0(Q
1
−
=
∂
∂
, (2. 2)
где
)]exp(y1/[)]exp(y1/[)y(I
11
α
τ
μ
α
τ
μ
−
−
+
+
−
+
= .
Аналогично, из
∞
=
∞ )(
i
π
для всех
i
следует ∞
=
∞
)(Q
1
и имеет место
)T2exp(x/)y,(Q
1
−
=
∂
∞∂ . (2. 3)
Подобные построения применимы и к отображению Q
2
.
При целых n
≥
0 обозначим x
n
=w
1
(2Tn+
α
) и y
n
=w
2
(2Tn+2T-
α
). Из формул
расщепления отображений и вытекает
1
Q
2
Q
Утверждение 3.5. Непрерывная модель (2.1) порождает дискретную
динамическую систему
x
n+1
=Q
1
(x
n
, y
n
), y
n+1
=Q
2
(y
n
, x
n+1
). (2. 4)
Каждая функция Q
i
обладает свойствами:
1) вогнута и возрастает по первому аргументу;
2) убывает по второму аргументу и Q
i
(0, z)=0 для всех z>0;
3) непрерывно дифференцируемо зависит от параметров
τ
1
,
τ
2
,
α
.
На основе соображений непрерывности приведем усиление третьего
свойства утверждения 3.5, когда в дискретной системе (2.4). один из параметров
τ
1
или
τ
2
может принимать значение
α
. Согласно рис. 3.3 при
1
τ
α
→ имеет место
)0(w)(w
111
+→
τ
α
. Поэтому для сохранения непрерывности по
1
τ
α
→ положим
