Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.

98
дифференциал
F
в точке
)t,X(
. Тогда для матрицы
)t,X(hDFEDL
+
=
свойство
ρ
в точке
),,( htX
о ределяется неравенством
0)]h,t,X(D[ >
п
L
ρ
. (2.2)
Актуальна задача: какие свойства матрицы
D
L наследую атрицей тся м
DP
?
При решении этой проблемы полезными оказываются следующие понятия.
1. Важное промежуточное положение между и занимают
L
()
httX
+
π ,,
P
–
локальные сдвиг-отображения за время
[
]
htt
+
, по траекториями (2.1) с
точке
началом в
X
при малых 0. Очевидно>h , L и
π
действуют в одном и том же
расши есьма эф
Лемма Адамара (см. Арнольд, 1984). Пусть u(h) – гладкая функция и u(0)=0
.
Тогда u(h)=hw(h), где w – некоторая гладкая функция.
ой гладкой
Адамаро авления:
1) , где - гладкая функция;
2)
hwhhuuhu +
, где w - гладкая функция.
В частности, справедливо представление
ренном фазовом пространстве
R . Ниже в фективной оказывается
1+n
Так, для произвольн функции u(h) последовательно получаем
вские предст
)()0()(
1
hhwuhu +=
1
w
)()0()0()(
2
2/
+=
2
()
(
)
(
)
htXGhhtXLhttX ,,,,,,
2
+=+π
,
где
()
htXG ,, – некоторое гладкое отображение.
2. Локальная универсальность
ρ
для
D
L означает: в каждой точке
неравенств торого
ин
)t,X(
о (2.2) выполняется для всех достаточно малых
h из неко
тервала
),0(
δ
. Разумеется,
δ
может зависеть от конкретной то . чки
)t,X(
Если в определении локальной универсальности верхняя граница
δ
не
зависит от
()
tX , на каждом и длины T ( т. е. с началом в точк
()
0,
0
X и ко о
куске траектори е
м в точке ), то будем говорить, имеет место равно ая нц
()
TX
T
, что мерн
локальная универсальность
ρ
для
D
L . Аналогично определяется равномерная
локальная универсальность
ρ
и для отображения
π
D
.
3. Назовем свойство
ρ
полугрупповым, если
()
0A >
ρ
и
(
)
0B >
ρ
из условий
следует неравенство
()
0AB >
ρ
. По сути, полугрупповые свойства – "мотор"

99
данной схемы наследования. Имеет место
Предложение 4.1. Пусть свойство
ρ
является полугрупповым и равномерно
локально универсальным для
π
D
, тогда отображение
DP
наследует
ρ
.
В связи с предложением 4.1 возникает проблема нахождения критериев
равномерной локальной универсальности
ρ
для
π
D
. Предлагаемый ниже признак
понятие грубости.
4. Пусть - произвольная точка. Рассмотрим представление
”равномерности” опирается на следующее
()
tX ,
()
)]t,X(hDFE[)]h,t,X(DL[h
+
=
=
ρ
ρ
ϕ
.
Согласно лемме Адамара имеет место представление
(
)
h,t,Xhba)]t,X(hDFE[
+
=
+
ρ
,
где
()
Ea
ρ
=
– константа и
(
)
htXb ,, – некоторая гладкая функция. Будем говорить,
что
ρ
– грубое свойство, если выполняется хотя бы одно из двух условий:
Г )
0a >
или Г
2
) если
a 0
=
, то
1
(
)
00,t,X >
для всех
()
tX , .
Согласно (Ильичев, 2003а) им место
Утверждение 4.3. Пусть грубо
b
еет
е свойство
ρ
локально универсально для
D
L , тогда оно равномерно локально универсально для иDL для
π
D
.
С учетом предложения 4.1. получаем достаточный и легко проверяемый
признак наследования
В качестве примера проведем глобальный анализ одномерного уравнения
),( txxfx
=
&
с приведенными ранее ограничениями н функцию
f
. Имеют место:
Свойство монотонности. Определим следующую функцию
а
Δ
Δ
ρ
≡
)(
.
Соответствующее свойство
0)( >
Δ
ρ
утверждает, что
Δ
- пол жительное число.
Здесь выполняется условие Г
1
, поэтому
о
ρ
– грубое свойство. Далее, имеет место
локальная универсальность, поскольку для каждой точки
()
tx, справедливо
неравенство
()
(
)
[
]
0x)t(,xxfh1xL >
∂
∂
+
=
∂
∂
β
ρ
при малых
h . Последнее, положительные числа образуют полугруппу по
умнож ению, поэтому
ρ
- полугрупповое свойство. Следовательно, 0>
∂
∂
xP .
Значит,
P
монотонно возрастает.

100
(
)
xy ln
=
Свойство сжимаемости. Сделаем замену , тогда данное уравнение
бретает прио вид
(
)
(
)
)t(,yexpfdtdy
β
=
.
Определи ю
)1()(
Δ
Δ
Δ
ρ
−
≡
. Соответствующее свойство
0)( >
Δ
ρ
м функци
эквивалентно
)1,0(
∈
Δ
. По ожим л
(
)
(
)
(
)
yexp)t(,yexpfh1y/L
x
β
Δ
′
+
=
∂
∂= .
Тогда с учетом
0<
′
x
f убеждаемся в грубости (см. условие Г
2
) и локальной
универсальности
ρ
. Последнее, числа нтервала из и
(
)
)1,0 образуют пол гру пу по у п
умножению, поэтому
10
<
∂
∂< yP . Следовательно, в данном уравнении может
существоват лишь одно пол равновесие ь ожительное
(
)
r
, которое глобально
во в
+
R . устойчи
по в Так
т о
4.3. Наследуемые знак-инвариантные структуры и
динамика конкурентов в периодически изменяющейся среде
Различные приемы зволяют расширить класс наследуемых свойст . , имеет место
Лемма 4. 4. Пусть каждое свойс в
i
ρ
является грубым и локально
универсальным для
D
L . Если
(
)
– полугрупповое свойство, тогда
1
,,min
ρ
ρ
K
=
n
ρ
D
P
наследует
ρ
.
Такие кусочно - гладкие свойств возникают при описании характера
мпонент П
возникают 16 типичных вариантов знаковой структуры матрицы
Всякая знаковая структура
а
монотонности ко отображения уанкаре. Например, для
RR:P →
.
//
//
2111
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂∂∂∂
∂∂∂∂
=
xPxP
xPxP
DP
22
2212
D
P может быть задана с помощью операции . В
частности, система неравенств
min
0 >
∂
∂
,
<
∂
∂
,
<
∂
∂
,>∂
∂
,/0/0/0/
22122111
xPxPxPx
вивалентна лишь одному неравенству
P
эк
()
0 >
∂
∂
,
∂
∂
−
,
∂
∂
−
,∂∂
22122111
////min xPxPxPxP .
Поставим теперь специальный вопрос о “наследовании”: пусть все
D
L
представляются одной и той же знаковой матрицей для всех ∑
X
и
t
, когда
D
P
101
описывается той же матрицей ∑?
Для удобства вместо знаков
+
и – будем писать 1
+
и 1− , соответственно.
Оказывается все такие (знак инвар антные) матрицы допускают полное описание
(Ильичев, Ильичева, 199 ормально, они задаются квадратной (размера
n
- и
9). Ф
n
×
)
таблицей
()
()
ijn
cc σ=
∑
,,
1
K
элементы которой равны
.
jiij
cc=
,
σ
Здесь каждый
параметр одно из двух значений . Например, при
2
=
n
i
c может принимать 1
±
существуют только две разные знак - инвариантные матрицы
() ( )
⎟
⎠
⎞
⎜
⎝
⎛
++
++
11
11
() ()
⎞⎛
−+ 11
⎟⎜
=−−=
∑∑
1,11,1
и
⎜
⎜
⎝
+−
=−=−
11
1,11,1
Весьма наглядным является представление матриц в виде
нтиро ющим
∑∑
⎟
⎟
⎠
)(
ij
aA =
орие ванных графов. Согласно (Робертс, 1986) граф строится следу
образом: если
0≠
ij
a
, то проводится ребро из вершины
j
в вершину . Величина
наз
ым, когда е е
о ст П
этом вершин ебра пол
отрицательны). К
двухпартийному а
ак – е соответствует
двухпа
ют первую партию, а остальные – вторую.
Тогда
⎝
−
mmmk
II
где ; - блок из столбцов и строк, состоящий только из 1. При
порядка преобразу у
структур
сс ,,K
.
Далее, матрицы с фиксированной знак - инвариантной структурой
образуют полугруппу по умножению. Из леммы 4.4 получаем
i
ij
a
ывается весом этого ребра. При
0>
ij
a
ребро считается положительным, и
отрицательным при
0<a
. Граф называется двухпартийн го в ршины
можно разбить на два непересекающих подмн же ва -партии
M
и
M
. ри
ы одного подмножества
i
M “дружат” (их р ожительны), а
вершины из разных подмножеств “враждуют” (их ребра
ij
1
2
графу относится и случай, когда одн из партий пуста.
Справедливо
Предложение 4.2. Зн инвариантной структур
ртийный граф.
Пусть первые
k
вершин составля
знаковая структура соответствующей матрицы имеет вид
⎜
⎜
⎛
−
kmkk
II
,
⎟
⎟
⎠
⎞
knm −=
pq
I
q
p
изменении нумерации вершин данная матрица ется в одн из
n1
()
∑
()
∑∑
=
n
сс ,,
1
K

102
еще ин достаточный принцип наследования.
Утверждение 4.4. Если все
од
D
L принадлежат одной и той же знак -
инвариантной структуре ∑, то и
DP
принадлежит ∑.
Пусть дифференциал отображения
P
описывается знак - инвариантной
структурой
(
)
∑
n
cc ,,
1
K
. Тогда для точек
(
)
n
aaA ,,K
=
1
и введем
отношение полупорядка
()
n
bbB K,
1
=
B
A
<< , которое имеет место
если
iiii
cbca
≤
для всех
ni K,,1
=
.
Такой полупорядок порождается некоторым конусом (Красносельский, Забрейко,
1975; Опойцев, 1986). В частности, “с точки зрения
(
)
∑
−1,1
” отношени е
B
A
<
<
эквивален но принадлежности вектора т
(
)
AB
−
четвертому квадранту пл
Непос
оскости.
редственно
устанавливается
если
B
A
<
<
, то и
(
)
(
)
BPAP
<
<
.
Пусть
B
A
<< . Рассмотрим конусный отрезок
П
}BXAX{)B,A(
<
<
<
<
=
.
“С точки зрения
()
∑
(
)
BAП ,
−1,1
”, множество является прямоугольником, в
котором самая “слабая” вершина
A
находится на северо-западе, а самая “сильная”
юго-востоке. Из монотонностивершина
B лежит на
P
сразу вытекает
под действием
P
образ конусного отрезка
()
BАП , вложен
онусный отрезок в к
(
)
(
)
(
)
BPAPП , .
Развитые еометрические представления примг енимы к исследованию
нкуренции
йствующих конкурентов описывается системой:
ко в переменной среде. Изложим их. Так, согласно общим допущениям
динамика двух взаимоде
(
)
(
)
txxfxxtxxfxx ,,,,,
2122221111
=
=
&&
, (3.1)
где любая
i
f строго убывает по каждой переменной
1
x и
2
x ; по переменной
t
гладкая функция
f являетс я
i
T
- периодической. Решения (3.1) т не быстрее
экспоненты, поэтому продолжаются вперед неограниченно.
Дифференциал
расту
локального отображения для системы (3.1) является знак -
инвариантной структурой
(
)
∑
−1,1
)
, и, значит, знаковая структура дифференциала
отображения Пуанкаре имеет тот же вид. Обозначим через и -
(P
1
P
2
P

103
координатное представление
P
. В силу предыдущего, каждая функция
в св
−
),(
0
2
0
1
xxPx
i
T
i
=
озрастает по " оей" переменной
0
x
и убывает по "чужой" переменной
0
x
.
Как и в
i i3
D
- системах поведение (3.1) определяется расположением изоклин.
Здесь изоклиной является следующее множество точек :
2
+
R
(
)
{
}
0,
00
2
0
>==
T
iiii
xxxxE ,
Приведем способ
где
2,1i = . эквивалентный определения данной изоклины
)x,x(Px
21ii
=
. (3.2)
При некоторых (вполне естественных) условиях множества и не
чае
1
E
2
E
пусты (Ильичев, Ильичева, 2002а). В этом слу уравнения
()
111
, xxP 0
=
и
()
222
,0 xxP = имеет единственное, положительное реш и
2
r ,
ответственно). Так как
0x/P
i3i
ение (
1
r
со
<
∂
∂
−
, то уравнение (3.2) разрешимо в
x =
−
форме
()
ii
xE при
(
]
ii
r,0x ∈ . Очевидно, )r(E0
iii3
=
. График каждой изоклины
оединяет оси координат ( рис. 4. 2). с
ривая “мягко притягивает” к себе векторное поле
i
E
P
К по - й координате.
Например, если
i
(
)
0
2
0
1
, xx
лежит ниже , тогд и только тогда) . “Мягкость”
заключается в том, что точка также находится ниже .
Утверждение 4.5. Пусть изоклина лежит выше , тогда в системе (3.
1) первый конкурент вытесняет второго.
Приведем идею обоснования данной теоремы. А именно, с помощью
"высокой" кривой построим "матрешку": - параметрическое семейство
стягивающихся конусных отрезков
1
E а (
0
11
xx
T
>
),(
0
21
xx
T
1
E
1
E
2
E
1
E k
()
(
)
{
}
BXAxxXkП
k
<
<
<
<
=
=
21
,
,
где из . Здесь подвижная самая "слабая" вершина
k
[]
1,0
()
111
, krEkrA
k
=
лежит на
кривой , а самая "сильная" вершина закреплена в точке
1
E B
0,
1
ζ
+r
, где
константа
0>
ζ
. При получаем наименьший прямоугольник 1=k
()
[
]
ζ
+
=
11
,1 rrП ,
который вырождается в отрезок на оси . А при образуется наибольший
1
x 0→k
прямоугольник П(0). Под действием отображения
P
большие прямоугольники
104
перехо П
дят в малые. В пределе возникает (1) – это и означает, что вторая
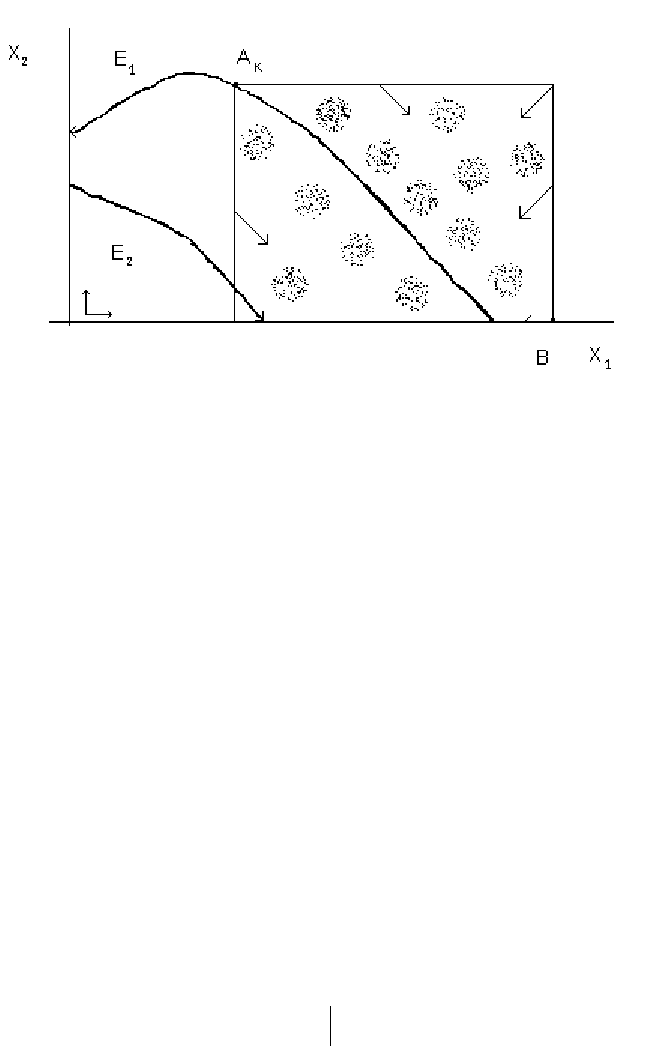
популяция вымирает (рис. 4.2).
Рис а
йствия конкурентов
. 4.2. Доминирующая изоклин и построение семейства вложенных кубов.
Рассмотрим теперь общую модель взаимоде
n
()
(
)
t,x,...,xfxx,....t,x,...,xfxx
n1nnnn1111
=
=
&&
,
(3.3)
; где каждая
i
f убывает по любой переменной
1
x , …, по переменной
n
x
t
гладкая
ункция
i
f является ф
T
- п ческой. ериоди
е
ге
При количеств конкурентов больше двух применение прежнего
ометрического подхода сталкивается с принципиальными трудностями: знаковая
структура
D
L не является знак – инвариантной (диагональ положительна, а все
остальные элементы отрицательны). Поэтому возникают проблемы с определением
свойств отображения Пуанкаре; далее, какие геометрические объекты
представляют изоклины
(
)
{
}
0xxRx...,,xE
T
i
0
i
n0
n
0
1i
>=∈=
+
систем
п
и с
ы (3.3) и др..
Тем не менее здесь возможен окольный уть. Так, в (3.3) изменим
направление времен
()
tt −→
. В новой истеме переименуем переменные
(
)
tyyfyy
niii
−
−= ,,,
1
K
&
, (3.4)
где
ni ,,1
. Дополнительно предположим, что решения (3.4) продолжаются
K=

105
впер ан ченно.
Обозначим через
)Q,...,Q(Q
n1
= - отображение Пу каре в системе (3.4).
Поскольку
Q
– обратное отображение к
ед неогр и
ан
P
, то векторное поле
Q
получается п
обращения стрелок в векторном поле
утем
P
. Очевидно, не одв точкип и ые жн
P
и
совпад у р
).
Дифференциал л .4)
с
Q
ают. Многие пол ченные езультаты в системе (3.4) доставляют ценную
информацию и для модели (3.3
Лемма 4.5. окального сдвиг - отображения системы (3
оказывает я знак - инвариантной матрицей
(
)
∑
1,,1 K
, диагональные элементы
котор
учае
ой больше 1.
Используя принцип наследования, пол м: в координатном представлении
(
)
00
,,
ni
T
i
yyQy K=
функция
i
Q возрастает
1
по каждой переменной и ,более того,
яте ва позволяют приме
Так, каждая изоклина системы (3.4)
1y/Q
ii
>∂ . Эти обсто нить к (3.4) развитые выше∂ льст
геометрические методы анализа.
()
{
}
0yRy...,,yJ
0n00
i
=∈= y
T
iin1
>
+
допускает
представлением изоклины
простое исследование. А именно, воспользуемся эквивалентным
)y,...,y(Qy
n1ii
=
.
С учетом вышеприведенных свойств функции
i
Q можно выразить
i
y через
остальные переменные. Обозначим данную функци через
,...,y(Jy
1ii
= , тогда
убы оим переменным.
, с
ю )y
n
i
J вает по всем св
Важно отметить что поверхно ть
i
J “отталкивает” от себя векторное поле
Q
по
i
- той координате. Например, если
(
)
0
n
0
2
0
1
y, ,y,y
лежит ниже J , тогда (
только тогда)
0
1
T
1
yy <
.
...
1
и
106
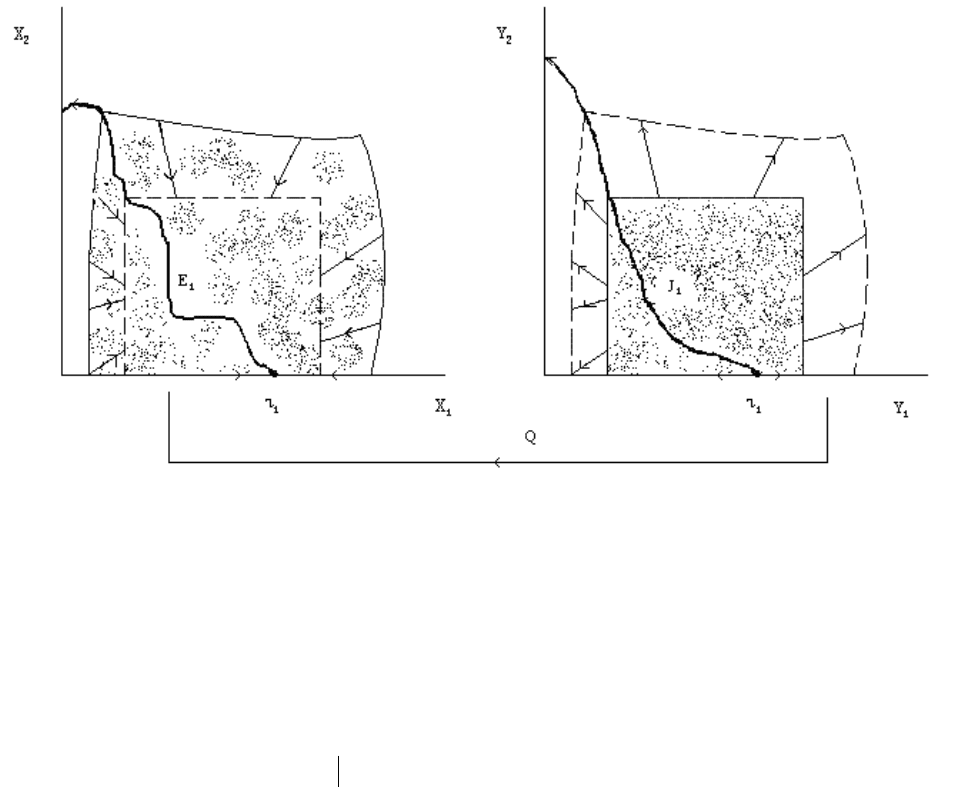
Рис. 4.3. Взаимосвязь динамических систем (3.3) и (3.4)
Установим геометрический признак отбора, основанный на взаимном
расположении изоклин. Определим в
n
R
+
следующее k -параметрическое
семейство вложенных призм ( рис. 4.3).
() ( )
{
ζ
+
≤
≤
=
π
1111
,, rykryyk
n
K
и
(
)}
1211
,,, kryykrQ
n
≤K
где
ζ
– некоторая положительная константа и 10 ≤
<
k ;
1
r удовлетворяет
уравнению
)0,...,0,r(Qr = . Отметим
(
)
1
π
– самая, что малая призма -
111
вырождается в отрезок
[]
ζ
+
11
, rr , лежащий на первой оси координат. При 0→k
возникает самая большая призма. Справедлива почти очевидная
Лемма 4. 6. Пусть изоклина
1
J расположена выше всех других изоклин.
Тогда на боковой поверхности призмы
(
)
k
π
векторное поле отображения
Q
направлено наружу.
По сути, вся подготовительная работа произведена с помощью " рошего" отображения Теперь заключительный шаг можно
осуществить в ра
Q
. хо
мках "плохого" отображения
P
.
ние 4.6. Пусть E распаложена выше всех другихУтвержде изоклин ,
Действительно, во вспомогательной системе (3.4) изоклина
J также будет
расположена выше остальных. Обозначим через
1 i
тогда первый конкурент вытесняет остальных.
1
E
(
)
kП
образ под действием
(рис. 4. 3). С увеличением криволинейная призма
()
kπ
Q
k
(
)
kП
сокращается и, наконец,

107
()
1П
в к
[
ырождается в отрезо
]
ξ
+
1
r на оси OX
1
, где константа
0>ξ
.
Векторное поле
1
,r
P
на границе
(
)
kП
направлено строго вовнутрь. Под
действием
P
фазовая точка (3.3) переходит из большой криволинейной призмы в
меньшую. В пределе данная точка оказывается в П(1). Это озн ает: все
популяции, кроме первой, вымирают
ач
.
новения изоклины в неавтономных
моделях конкуренции. Универсальная константа запаса
В связи с приведенным выше признаком отбора становится актуальной
Здесь требуется более конкретная информация о характере
конкур
моделей (Ильичев, Ильичева, 2000; Ильичев, 2001б):
4.4. Условие возник доминирующей
проблема определения условий, когда одна из изоклин лежит выше всех
остальных.
ентных взаимодействий популяций. Так, рассмотрим следующий
распространенный класс
(
)
(
)
[
]
niii
xxVxx t
+
+
+
−
= K
&
1
1
β
, )
где
ni ,,1 K=
;
(4. 1
(
)
t
i
β
– максимальная cкорость роста
i
- го конкурента в зависимости
от факторов среды. Предполагаем, что
()
t
i
β
T
- периодических – положительная
T
(
)
zV
- периодическая функция. Гладкая, положительная возрастающая функция и
(
)
10V
)
учитывает негативное действие конкуренции. Положим
=
и
(
∞
=∞V
.
Обозначим через . Пусть функция к , тогда
ловия запаса
∫
=
T
ii
dttT
0
)()/1(
βλ
v
V
– обратная
оказывается при выполнении ус
(
)()
(
)
Tvv expλ>λ для всех
1>i
. (4.2)
изоклина
E
лежит выше всех друг .
i1
их Сначала установим частный случай:
1
Утверждение 4.7. При условии запаса для
2
=
n
изоклина
1
E
лежит выше
2
E
.
Согласно предыдущему разделу при удобно сделать обратную замену
времени и перейти к новым перемнным
3≥n
tt −→
(
)
(
)
[
]
yyVtyy
niii
+
+
−
−
=
1
K
&
1
β
, (4. 3)
Напомним определение изоклина в данной системе
()
{
}
0yyRy...,,yJ
T
i
0
i
n0
n
0
1i
>=∈=
+
.
