Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.


88
Доказательство утверждения 3.2. Прежде всего, заметим след
зад
ующее. Пусть
аны две последовательности и
{
}
i
τ
′
′
{
}
i
τ
′
, а
B
′
и
B
′
′
– соответствующие им
матрицы взаимодействий, тогда
B
′
′
′
и подобны. Действительно, возьмем
B
диагональную матрицу
U
, в которой
(
)
ii
u
ii
′
′
τ
−
τ
′
=
exp . Тогда . В этой
связи
BUBU
′′
=
′
−1
достаточно рассмотреть матрицу
*
rB
, соответствующую набору
()
nTi
i
1−=τ для
ni ,,1 K=
. Элементы каждой строки
*
rB
являю екоторо
перестановкой чисел
тся н й
(
)
(
)
(
)
nnrnTr 1exp,,exp,0 T
−
−
⋅
−
⋅ K .
Кроме м трица неотрицательна и неразложима. о теореме
Фробениу у нее существует единственный неотрицательный
собственный вектор
того, эта а П
са-Перрона
(
)
*
X
с положительным и максимальным (по модулю)
собственным значением
(
)
*
γ
(еллман, 1976). В данном случаеБ имеем
и
()
1,,1,1
*
K=X
(
)
(
(
) )
]
nnT 1−−K
.
Поэтому условие продуктивности эквивалентно
γ
.
Доказательство леммы 3.2. Воспользуемся следующей эквивалентной
ктор
[
nTr expexp
*
++−=γ
*
<
1
лежит на границе
(
)
ε
П
формулировкой: если положительный ве
Y
, тогда
принадлежит
()
YP
внутренности
(
)
ε
П
.
Итак, пусть для всех . Отображение
iii
Aya ≤≤
i
P
является композицией
ображений , поэтом дос в
атием по той координате. Возьмем для примера отображе
, которое преобразует лишь первую координату. Обозначим
1
K
простых от у таточно устано ить: всякое
i
G
является сж
1
GG
n
oKo
()
εП
i
- ние
1
G
()
n
yyygy ,,,
21
)
1
= .
оему т место В силу монотонного роста
1
g по “св ” аргументу, имее
(
)
(
)
nn
aaAgyyygy ,,,,,,
2112111
KK
)
<
=
Далее из (1.11) следует: если
2111
.
, соотношения
()
0,,,
<
=
n
aALI K , то
1211
,,aAg K . В этой связи, определим знак линейной формы
a
, Aa
n
< при
1
yA
()
1
L
(
)
ε−=
ii
ya
*
1
,0max
ε+
1
*
1
z
и
z=
(
)
(
)
0,,
221111
=−−+≤ zyzyzyI
nn
εεεε
K
.
1,
1
***
<− rTzL
γ
Следовательно, получаем оценку сверху
11
Ay
<
)
.

89
С др гой сто из моното ну роны, н ого убывания по “чужим” аргументам
вытек
1
g
ает соотношение
(
)
nn
AAagyygy ),,
11
>= K
)
,...,,(
2111
.
I еПри 0
1
>a из
()
0,,,
211
>=
n
AAaL K следу т
(
)
12111
,,, aAAaLg >
2 n
=
K . В этой
связи, определим знак выражения
()
0/)1(,,,
12212 11
>
−
=
+
+
−
=
rTzzyzyzyLI
mm
.
ε
ε
K
Отсюда получаем оценку снизу
11
ay >
ε
ε
γ
)
. А если
1
0
=
a , то и подавно
0
11
=
> ay
)
.
y
Доказательство леммы 3.5.
Введем обозначение
() (
i
yYYG
)
)
)
)
n
K,
я
, г лементы расщепления отображения Пуанкаре .
Сравн
,
1
==
дл
всех де
{}
i
G – э
i
1
GGP
n
oKo=
им значения
()
LL =
и
Y
(
)
*
YLL
i
всех
i
. Здесь возм следующие
=
для ожны
три варианта.
ч1. То ка
Y
лежит ниже E , тогда ryL
11
−
λ
=
1
. С иленной лемме
поглощении точка
огласно ус
3. 3 о
Y
)
также лежит ниже и, значит,
1
E ryL
111
)
−=
λ
.
иПри
1=i
меем
1
*
1
y >
, поэтому LL
y
<
1
.
А при
1>i
получаем
1
*
1
yy =
и здесь LL
=
1
.
2. Точка
Y
ryybL
n
j
j
2
1
=
∑
=
лежит выше
1
E , тогда
j 11
−λ>
.
Пусть сначала . В силу леммы 3.3 точка
Y
)
1
=
i
также лежит выше и, значит,
j
L
2
1
огласно определению отображ имеем
1
E
∑
yb
1
)
. С
=
=
n
j
j
ения G
1
jj
yy =
)
для всех
1>
j
и поэтому .
сть еперь тогда
LL =
1
, а остальные координаты точек
Y
)
ii
yy
<
)
Y
Пу т , и
1>i
совпадают. Рассмотрим три возможных положения точки
Y
)
:
2а)
Y
)
лежит выше
1
E , тогда
∑
=
jji
ybL
1
)
. азанных суммах имеет место
=
n
j 2
В ук
i
yy <
)
и
jj
yy =
)
i
при
i
j
≠
. Значит LL
i
<
;
2б)
Y
)
лежит же
1
E , тогда ни ryL
1i 1
)
11
yy
=
)
−
=
λ
. Поскольку
1≠i
, то .
Значит
LryL
i
<−λ=
11
;

90
2в)
Y
)
лежит на , тогда
1
E
ryybL
n
))
j
jji 11
2
1
−==
∑
=
λ
. Так как
11
yy
=
)
и
Lr < , то LL
i
<
3. Точка
y−λ
11
.
Y
лежит на
1
E . Здесь легко видет LL
i
ь, ry
11
−
=
λ
=
для
всех
i
.
Теперь рассмотрим более внимательно результаты проведенного выше
анализа, которые сведены в таблицу (см. таблицу). Из нее находим: если
Y
не
на , то
))()
YLPL <
и, следовательнолежит
((
Y
1
E ,
(
)
(
)(()
YPLYPPL
)
<
.
Таблица П.1. Поведен н
ие фу кции
L
при действии простых отображений
i
G
Y
выше
1
E
Пол ение ож
Y
и
Z
Y
ниже
Z
выше
или на
Z ниже
1
E
1
E
1
E
Y
О
тображение
на
1
E
1
G
LL <
1
LL
=
1
LL =
1
LL
=
1
1
G
при
1>i
L =
1
LL L
<
1
L L<
1
LL
=
1
*В таблице использовано обозначение Y
Z
)
=
.
Пусть теперь
Y
находится на , но так как
1
E
(
)
YP
всегда оказывается ниже
1
E , то окончательно находим
(
)
(
)
(
)
(
)
(
)
YLYPLYPPL
=
<
.
Доказательство леммы 3.11. Рассмотрим для примера поверхности и
в . Пересечение
OY в точках
1
E
2
E
3
+
R
оси
2
поверхностями
1
и
2
происходит E E
[
)(
121
*
2
bTy
μ
= и
(
)
]
2
**
2
1 μ= Ty
,
ветственно. По полняе
exp −−
соот условию имеем
**
2
*
2
yy >
, поэтому вы тся неравенство
(
)
(
)
[
]
TT 1expexp
2112
−
τ
−
τ
>
μ
μ (П. 1) .
Теперь в точке
(
)
0,,0
*
2
y
из построим касательную плоскость (см. рис.
3.7). Напомним, что для произвольно поверхности в точке
1
E
1
L
0),,( =zyxH
й
),,(
0000
zyxp = касательная плоскость имеет вид
0)()()(
000
=
−
+
−
+
−
zzCyyBxxA ,
где ,
/
pHC
z
=
В данн
)(
0
/
pHA
x
=
)(
0
/
pHB
y
=
,
)(
0
.
ом случае имеем
=
H
1111
yybf
n
jj
μμ
−
⎟
⎟
⎞
⎜
⎜
⎛
∑
и 0
00
== zx , /(
0
. Ty
=
1j
⎠⎝
=
)
112
b
μ
91
Поэтому ,
1
]1)/[exp(
и , где
1
μ
−=A
12
−= TTbB
μ
−
]1)/[exp(
=
−
131
TTbC
μ
−
- элементы Вольтеровской матрицы взаимодействий при
3,2
=
i
)exp(
11 ii
Tb
τ
τ
−+= .
Окончательно, уравнение касательно плоскости преобразуется к виду: й
.
113312
/]1)[exp(
21
Ty byT
μ
Tby
+
−
=
+
Ввиду выпуклости , плоскость лежит ниже .
ввиду клости
ости осей координат
c
ющи
1
E
1
L
1
E
Теперь покажем, что
1
L лежит выше
2
E . Здесь, выпу ,
достаточно установить: точки пересече ерхн
2
E
2
E лежатния пов
ниже точек пересечения
1
L соответствующими осями координат. Так,
1
L имеет
следу е точки пересечения.
(
)
[
]
)1exp(
1
2*
1
−= TTy
μ
и
)(
131
bTy
μ
=
.
А поверхность
2
E пересекает указанн
*
3
ые оси в точках:
)(
212
**
1
by
μ
= и T
)(
232
**
3
bTy
μ
=
1221
,
где
)exp(
τ
τ
−=
3223
b
и )exp(
+
τ
−
τ
= Tb . При условии (П. 1) получаем
yy
для
всех ду поверхностями и . Значит,
находится
***
ii
>
i
. Таким образом, плоскость
1
L лежит меж
1
E
2
E
1
E выше
2
E .
Рис. 3.7. К обоcнованию леммы 3.11. Изоклины и разделяющая их гиперплоскость.
92
ГЛАВА 4
ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ МОДЕЛЕЙ КОНКУРЕНЦИИ.
ПРИНЦИП НАС
…
тической пустыней,
заполненной одними лишь вычислениями…
(Арнольд В.И Второй закон Кеплера и
топология абелевых интегралов)
о енности
ЛЕДОВАНИЯ
двухсотлетие от Ньютона до Римана и Пуанкаре
представляется мне матема
.
Достаточн общая модель динамики числ
()
x
одной популяции
представляется в форме (Vance, Coddington, 1989):
),,( txxfx
=
&
где – время; – гладкая,
),( txf
T
t
– периодическая (по времени) функция роста;
∂∂ xf
ид
ьное значение , и
поэтому переменная
0<
при всех
()
tx, – условие негативного действия внутрив овой
конкуренции на рост численности популяции. Начал
/
0
0
≥x
x
будет оставаться неотрицательной и при всех
0>
t
.
Дополнительно будем предполагать: 1) при достаточно больших
x
полняется условие
0),(
вы
<
txf
при всех
t
. Данное неравенство "не позволяет"
численности неограниченно возрастать; 2)
0 >,t)f(
хотя бы для
некоторых
0>
популяц ии
0
t
(иначе популяция о о вымирает).
Ниже для описания динамики взаимодействующих конкур нт
днозна
е ов будет
испол
iii
чн
ьзована модель:
,t),,...,x
n1
(xfxx
=
&
где
ni ,,1 K=
;
i
f – гладкая,
T
– периодическая (по времени t) функция. Данная
система представляет собой естественное обобщение предыдущей модели с
граничениями. Так, всякая функция
i
f строго убывает по прежними о каждой
компоненте
(
n
xX = пр нулев векторе выполняется
от
вектора
);,...,
1
x ом
)(0
и
неравенство
()
0, >tf
i
0 х я бы для некоторых
0>t
;
(
)
0, <tXf
i
, если норма
X
достаточно велика. В данной мо переменная
()
tx
i
рдели каждая тет не быстре
, где по всем
ас е
()
tk
i
exp
()
tfk
ii
,max 0=
t
из
[
]
T, . 0

93
Значи является
фазов
данной г
в постоян
ес х д
простейший случай, когда гладкая правая часть не зависит от
n
R
+
т, её решения продолжаются вперед неограниченно. Замыкание
ым пространством данной системы.
Цель лавы разработка геометрических методов для анализа
динамики конкурентов (Ильичев, 2002а – 2002г).
4.1. Доминирующая изоклина и отбор ной среде
Приведем тественные под оды ля исследования моделей конкуренции,
основанные на геометрии расположения изоклин. Сначала для иллюстрации
рассмотрим
t
:
(1.1)
где ; для всех
),,...,(
1 niii
xxfxx =
&
;
(
)
0;0)(
<
> Xff
ii
0
,
ni ,,1 K=
0/ <∂∂
ji
xf
j
i,
если хотя бы одна из
но вкомпонент вектора
),,(
1 n
xxX K= доволь елика; начальный вектор
0
X
принадлежит
n
R
+
.
Для каждого
i
в замыкании
n
R
+
изоклину определим
(
)
}.0|{
=
=
XfXE
ii
при
i
, если и надлежит только еслиE 0x
i
=dtd . В силу Очевидно, точка
X
приведенных ограничений на
i
f , множество
i
E – непусто. Далее,
0
<
/
∂∂
ii
xf и
,значит , применима теорема о неявной функ к уравнению
Xf
i
,
напри
ции
()
0= . Отсюда
мер, при
1
=
i
находим гладкое решен ие
(
)
n
xxx ,,
211
KS
=
.
клина представляет собой поверхность, которая збивает
n
R
+
на
две связны ласти. Одна з этих областей ограничена
Всякая изо ра
е об и
(
)
{
}
0>
=
XfXB
ii
и примыкает началу к ор ат а другая – неограниченна. дем говор ть: точка к о дин , Бу и
X
находится ниже
i
E , если она принадлежит . Для той компоненты такой
i
B
i
-
точки , если
(
)
0
<
Xf
i
имеем
0>dtdx
i
. Аналогично, точка
X
находится выше
i
E .
Это условие порождает неравенство
0
<
dtdx
i
. Грубо говоря, тая компонента
орного поля (1
сущ
i
-
вект .1) устремлена ("притягивается") к своей изоклине
i
E .
Скажем, что в системе (1.1) ествует доминирующая изоклина
1
E , если

94
все “остальные ”изоклины
{
}
n
EE ,,
2
K лежат ниже
1
E . (1.2)
Ниже удет показано, что данное достаточное условие характери
популяцию как "самую сильну
б зует первую
ю". Предварительно обсудим поведение функции
xS ,
21
с
.
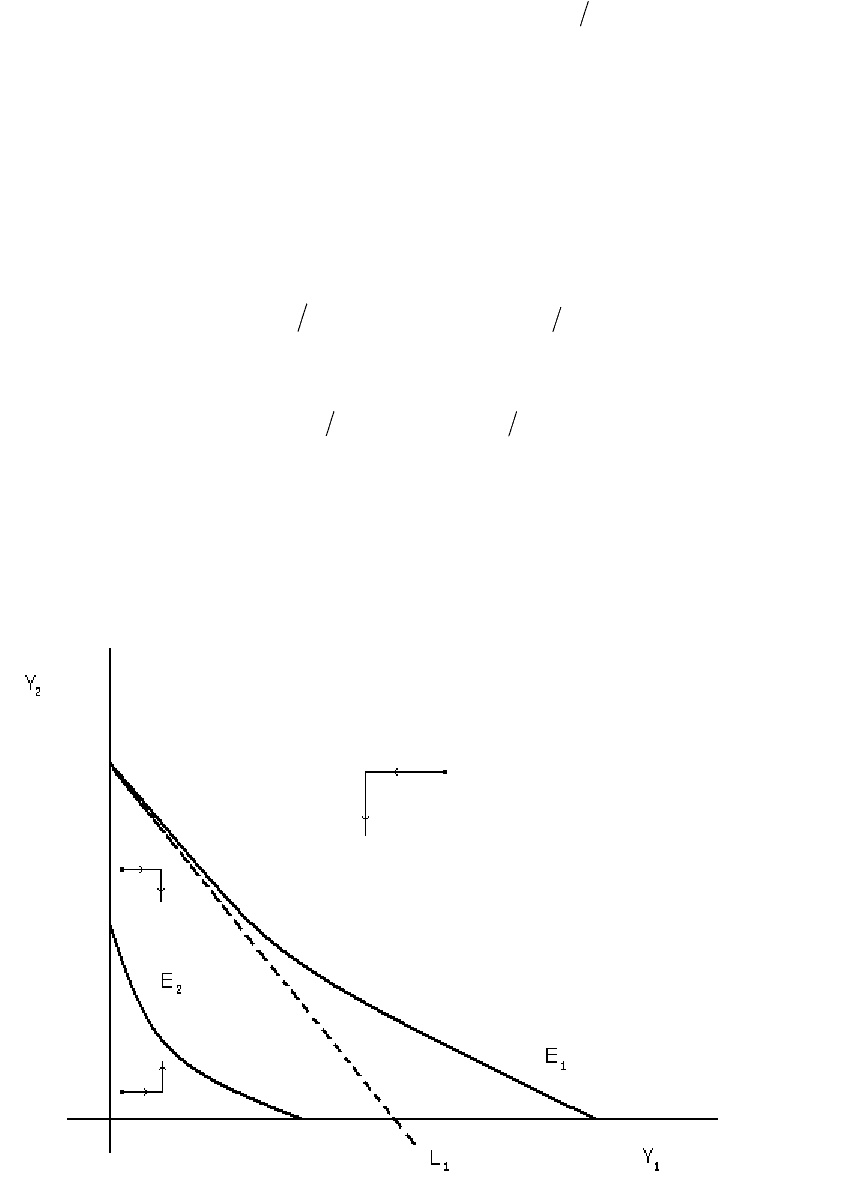
Отметим, что область примыкает к началу координат. Пусть изоклина
пересекает ось в точке , где
()
n
x,K , которая определена лишь для аргументов из " воей" области
}0),...,,0(|),...,{(
212
≥=
nn
xxfxxb
b
1
E
1
x
1
r
(
)
0,,0
11
KSr
=
. Очевидно, точка
)0,....,0,(
11
rR
=
является равновесием в системе (1.1). Имеет место
Лемма 4.1. Функция строго убывает по каждой переменной.
Теперь доопределим функцию для остальных неотрицательных
переменных с сохранением ее монотонных и непрерывных свойств. Так,
1
S
1
S
{}
n
xx ,,
2
K
введем вспомогательную функцию
(
)
n
xx ,,
2
K
λ
=
λ
, которая удовлетворяет
соотношению
(
)
.0,,,0
21
=
λ
λ
n
xxf K
Очевидно,
λ
определена при ех неотрицательных вс
{
}
n
xx ,,
2
K и
1>
λ
для
внешних точек области
b (= лежащих вне ). Из теоремы о неявной нкции,
устанавливаем:
b фу
λ
n
xx ,,
2
K – трого возрастает по каждой переменной
гладкая и с
функция. Положим
()
()
; точекных b
K
, для внутренних точек имеем , а для внешних – находим
()
[]
⎩
− .точеквнешнихдля,,,1
21
2
bxxr
n
n
K
λ
В частности
⎨
⎧
=
граничивнутреннихдля,,,
,
21
xxS
xxS
n
K
b
0>S
0
<
S
.
На границе
b одновременно выполняются равенства 0
1
=
S и , поэтому в
любом ц
1=λ
случа
0=S
. В елом,
S
– непрерывная и, более того, кусочно-
дифференцируемая функция. Для всякой частной производной по переменной
i
x
(при
1>i
) имеют есто
0 S
е
м
<
/
∂∂
1 i
x при bxx
n
∈
)...,( и ,
2
0
>
/∂
∂
i
x
λ
при x ,...,(
2
bx
n
∉) .
учетом конструкции функции по
каждо
Отсюда с устанавливаем, что и она убывает
S
й из переменных
{}
n
xx ,,
2
K .
95
Используя функцию
S
, построим в
n
R
+
поверхность
I
, леж
1
E ащую между
и изоклинами. Поверхность
I
и остальным
)(kI
=
будем искать в следующей форме
n
S при ,
ом и
),...,(
21
kxkxx = фиксированном параметре k . Очевидно
)1(I
совпадает с
1
E .
При всех
1k множество
)(kI
оказывается же
1
E , за исключением общей
точки
1
R . Далее,
)(kI
непрерывно зависит от k , по
1
> ни
эт у при
1≈k
<
k
она
лежит выше всех ”остальных” изоклин в
n
R
. Значит, для екот рого
*
k
получаем
искомую промежуточную поверхность.
н о
+
Построим в замыкании
n
R
непрерывную функцию:
+
(
)
},,,,,max{)(
*
211111 n
K
1 n
K
1
*
xkxkSrrxxrXL −−−=
где
xxX = . Поскольку функция – убывающая, то r – ее максимальное
значен
()
.,,
S
ие и, значит,
()
0≥XL
. Величина
0
=
L
реализуется при (и
равенстве в операции
max
только при)
трех аргу Такая ситуация возникает лишь в
равнов
всех ментов.
есной точке
1
R . Пусть
(
)
tX
– траектория (1.1), выходящая из
1
0
RX ≠
.
Обозначим
() ()()
tXLtL
=
. При условии (1.2) имеет место
Лемма 4.2. На траекториях системы (1.1) функция строго убывает.
()
tL
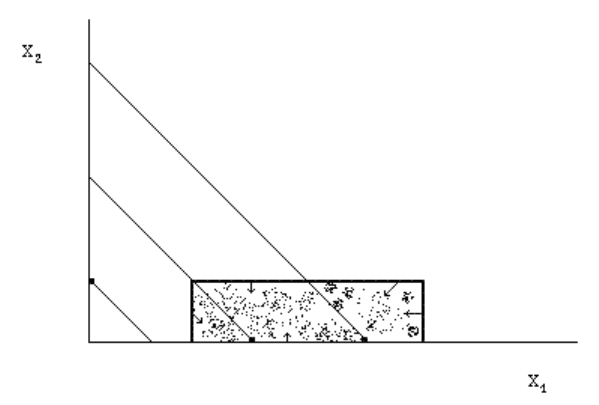
Рис. .1. Призма с векторным по ем вленным вовнутрь 4 л , напра
леммы 4.2. (рис. 4.1) Пусть
0
Приведем полезную геометрическую трактовку
.
1
r Заметим, что множество всех < ε<
X
, удовлетворяющих условию
(
)
ε
≤
XL
,
представляет собой кривол ю призму инейну
(
)
ε
П
:
96
1
r
ε
≤
− |
1
x и |
(
)
ε
−≥
*
2
*
,, rxkxkS
n
K
.
Тогд на границе оле направлено в внутрь призмы. Отмет что
()
0П
совпадает с равновесной точкой
1
R . Отсю
1
а векторное п о им,
да легко следует
о
Одним из частных случаев конкуренции ляется взаимодействие так
ае предполагается:
всякая
е
()
εП
Утверждение 4.1. При условии (1.2) в системе (1.1) равновесие
1
R глобально
устойчиво.
Иными словами, первая п пуляция вытесняет остальных.
яв
называемых "близких" (родственных) популяций. В этом случ
функция
i
f с одинаковой скоростью убывает по каждой переменной.
Формально, в любой точк
X
из выполняются соотношения
n
R
+
()
(
)
.//
1 nii
xXfxXf
∂
∂==∂∂ K (1.3)
услов одноместная функция ,
которая связана с функцией равенство
Лемма 4.3. При ии (1.3) существует
i
g
i
f м
(
)(
.,,
11 nini
xxfxxg KK
)
=
+
+
В этом случае одель близких конкурентов п м ринимает вид
где
i =
(1.4)
()
,
1 niii
xxgxx ++= K
&
n,,1 K
; каждая )(zg
i
- строго убывающая функция. Пусть
()
0
=
ii
rg
, тогда
зад
i
E ается уравнением
in
rxxx
=
+
+
+ K
21
. Поэтому здесь каждая изоклина
i
E –
гиперп нкция
211
лоскость. Отметим, что в данном случае фу
1
S задается уравнением
()
xxxr +++− ... при
n
(
)
rx
12
x
n
≤
+
+
K
у п
. Используя приведенную ыше
процедур родолжения
1
S до
S
, устанавливаем: данное линейное представление
имеет место для
S
и в случае
в
(
)
rxx > .
12 n
+
+
K
Будем предполагать, что в модели (1.4) выполняется условие доминации
(1.5)
В этом ся
утверждения 4.1 сразу получаем
едствие 4.1. При у и ) равновесие
глобал устойчиво в .
возможен обмен мутантными формами
или происходит инвазия форм. Тогда простейшая модификац
i
rr >
1
для всех
1>i
.
случае изоклина
1
E располагается выше остальных
i
E , поэтому реализует
условие (1.2). Отсюда с учетом
Сл слови (1.5) в системе (1.4 )0,...,0,(
11
rR =
n
R
+
ьно
В сообществе близких популяций
ия модели (1.4) имеет
97
вид:
(
)
,
1 inii
xgxx
i
x
μ
+
+
+
=
K
&
(1.6)
где
ni ,,1 K=
; 0>
i
μ
для всех i . Справедливо
Утверждение 4.2. системе (1.6) существует В единственное
полож
ую тономн
ительное глобально устойчивое равновесие.
4.2. Принцип наследования в динамических системах
Рассмотрим произвольн неав ую динамическую систему с гладкой,
- периодической, правой частью
T
(
)
tXFX ,
=
&
, (2.1)
где – с компонентами
n
xx ,,
1
K ;
n
FF ,,
1
K – компоненты отображениявектор
F
;
X
)Tt,X(F)t,X(F
ii
+
= для всех и n,...,1i
=
X
,
t
. Предполагаем, что решение (2.1)
сущес и
ее траекториям
во време интервале
твует и продолжается вперед неогран ченно.
Здесь ключевую роль играют свойства сдвиг-отображения по
[
]
htt
+
, . Обознач м данное отображение через нном и
(
)
htXQX
tht
,,=
+
, где 0>h . Особо выделим сдвиг - отображение Пуанкаре,
которое будем записывать кратко
(
)
0
XPX
T
= . Пусть ( ,..
1
P ).,
n
P – компоненты
отобра , тогда дифференциал
P
– это nn
×
матрица
( PDP
жения
P
)/)(
ji
xX∂=
∂
,
зависящая от . Свойства матрицы
DP
во многом
X
определяют поведение системы
Формализуем понятие свойства. Пусть
(2.1).
ρ
– гладкая ф , определенная
Напри
ункция
на
n×
матрицах. мер,
][
n
D
P
ρ
– определитель матрицы
DP
. Буд м
говорить: матрица
е
D
P обладает свойством
ρ
, если в каждо ке й точ
X
выполняется
>
неравенство
X(DP[
ρ
0)] .
Поиск о
е вой аппроксимации
локаль
таких глобальных свойств оказывается трудн й задачей.
Гораздо легче находятся свойства дифференциала эйл ро
ных отображений
(
)
(
)
tXhFXhtXLX
tttht
,,, +==
+
,
где
h положительно и мало. Обозначим через
E
– единичную матрицу и
DF
–
