Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.

48
Отсюда, в частности, следует единственность положительного,
T
-
периодического режима.
2.2. Стабилизация в двумерных системах
По сравнению с одномерной моделью в многомерных системах ситуация
усложняется. Так, можно “испортить” устойчивое равновесие при неудачном
выборе допустимых параметров перехода в пассивное состояние (и наоборот).
При обсуждении проблемы локальной стабилизации рассмотрим двумерную
систему линейных уравнений (=линеаризацию модели вблизи равновесия):
2121111
xaxax
+
=
&
,
2221212
xaxax
+
=
&
, (2.1)
где все – вещественные числа. Обозначим через – определитель матрицы
. Добавим к каждой из переменных модели (2.1) свое пассивное
состояние, тогда получаем расширенную линейную систему:
ij
a
d
)a(A
ij
=
,sqxps,sqxps
,sqx)pa(xax
,sqxax)pa(x
2222211111
2222221212
1121211111
−=−=
+−+=
+
+
−
=
&&
&
&
(2.2)
где и – положительные управляющие параметры. Отметим, что в
характеристическом уравнении для (2.2) свободный член равен . Поэтому
неравенство – необходимый признак стабилизации. При этом условии
справедливо (Ильичев, 1995б, 1995в)
}p{
i
}q{
i
dqq
21
0>d
Утверждение 2.6.
Нулевое равновесие модели (2.2) стабилизируемо при
подходящем выборе управляющих параметров, за исключением “плохого” случая,
когда одновременно выполняются неравенства
. (2.3)
0,0,0
21122211
≥>> aaaa
Во многих случаях стабилизация достигается, когда параметры - малы,
а - достаточно велики. В этом случае биомасса всех пассивных состояний
становится довольно большой, и она выступает в качестве демпфера.
}q{
i
}p{
i
Легко показать, что “плохой” случай (2.3) соответствует в исходной модели
(2.1) равновесию типа неустойчивый узел. Поэтому здесь колебательная
неустойчивость является “хорошим” случаем и, значит, стабилизируема. Такая
ситуация реализуется при нелинейных взаимодействиях типа “хищник-жертва”:
49
x
yyy
x
x
y
x
−
=
−
=
&&
,
,
в которой неустойчивое равновесие <1,1> становится устойчивым, если к каждой
переменной добавить свою пассивную стадию с параметрами
2
21
=
= pp и
. Напротив, при конкурентном взаимодействии
5.0
21
== qq
x
yyy,
x
y
x
x
−
=
−
=
&&
,
равновесие <1,1> не стабилизируемо, поскольку здесь
0
<
d .
Представляет интерес проблема:
когда достигается стабилизация
неустойчивого равновесия в многомерной линейной системе с помощью процесса
образования пассивных состояний?
Здесь, вероятно, достаточно потребовать
отсутствия положительных корней в матрице исходной линейной системы..
Последнее. При приведем один любопытный пример стабилизации.
Так, известная в гидромеханике система Лоренца (Каплан, Йорке, 1981):
3=n
()
3x8xxx,xxxx28x,xx10x
321331212121
−
=
−
−
=
−=
&&&
,
имеет
три
неустойчивых
равновесия
()
0,0,0
1
=r и
(
)
27,72,72r
2
= ,
(
)
27,72,72r
3
−−=
.
Добавим к каждой переменной пассивное состояние с
параметрами
i
x
i
s 1.0
=
i
q и
10=
i
p . Численно установлено: в зависимости от начальных условий переменные
расширенной модели притягиваются к точке ( , ) или к точке ( , ).
2
r
2
100r
3
r
3
100r
2.3. Пассивные состояния и динамика близких конкурентов
Выше было показано, что механизм образования пассивных состояний не
способен стабилизировать конкурентное взаимодействие. Покажем справедливость
этого утверждения и в достаточно общей ситуации. В этом разделе удобно
включить некоторый биологический параметр
α
в правую часть уравнения (1.1):
),x(xfx
α
=
&
(3.1)
где
х - численность и
α
- параметр. Трофическая функция f учитывает процессы
внутривидовой конкуренции, поэтому
f монотонно убывает по х. Дополнительно
предположим:
f(x,
α
) - гладкая по x и
α
; f(0,
α
)> 0 - условие
невымирания;
−∞=
∞
),(f
α
- условие ограничения численности популяции.
Например, в рамках Вольтерровской схемы имеем
x)(),x(f −
=
α
ϕ
α
.
50
Из приведенных ограничений вытекает однозначная разрешимость
уравнения
0),x(f =
α
. Пусть
)(x
α
ϕ
=
- решение этого уравнения, тогда
)(
α
ϕ
-
положительное, глобально устойчивое равновесие в модели (3.1). Данное
стационарное состояние назовем потенциальной численностью популяции.
Рассмотрим теперь сообщество из
n близких конкурентов , каждый из
которых характеризуется своим параметром
}x{
i
i
α
. “Близость” означает, что
популяции оказывают одинаковое конкурентное давление:
nii
xXfxXf
∂
∂
==∂∂ /),(..../),(
1
α
α
для всех i при . ),...,(
1 n
xxX =
Тогда их динамика описывается простой системой (Ильичев, 1992б):
),x...x(fxx
1n111
α
++=
&
, …., ),x...x(fxx
nn1nn
α
+
+
=
&
, (3.2)
где для всех . При таких начальных условиях траектории (3.2) не
покидают положительный квадрант, а решения продолжаются вперед
неограниченно. Обозначим
0)0(x
i
> n,...,1i =
)(c
ii
α
ϕ
=
и пусть . Очевидно,
точка - одно из равновесий (3.2). Имеет место (Ильичев, 1992б)
0c...cc
n21
≥≥≥>
>=< 0...,0,cr
1
Предложение 2.1.
В модели (3.2) равновесие
r
глобально устойчиво.
Здесь непрерывная функция Ляпуновского типа
}x...x,cx,xcmax{L
n21111
+
+
−
−
= . (3.3)
строго убывает на траекториях системы (3.2).
Таким образом, в сообществе близких конкурентов селективное преимущество имеет
популяция с наибольшей потенциальной численностью.
Простым обобщением модели (3.2) является следующая система, в которой
допускается поступление популяций извне:
1111
)S(fxx
μ
+=
&
, , ...
nnnn
)S(fxx
μ
+
=
&
, (3.4)
где ;
n1
x...xS ++= 0
i
>
μ
- приток
i
-той субпопуляции; ),S(f)S(f
ii
α
= .
В главе 4 будет показано, что в модели (3.4) существует одно положительное
равновесие. Обозначим через - обратную функцию к и .
Тогда непрерывная функция
1
i
f
−
i
f
)z(f)z(h
1
ii
−=
−
)}x/(h),...,x/(h,x...xmax{L
nnn111n1
μ
μ
+
+
=
, (3.5)
строго убывает на траекториях (3.4). Минимум достигается при равенстве всех
аргументов операции
L
ma
x
. Отсюда вытекает глобальная устойчивость данного

51
равновесия.
Пусть теперь каждая популяция обладает своим пассивным состоянием
и переходы
i
x
i
s
ii
sx
↔
описываются согласно схеме (1.3). Тогда модель (3.2)
преобразуется к форме:
iiiiiii
qspx)S(fxx
+
−=
&
,
iiiii
qspxs
−
=
&
, (3.6)
где ; допустимые параметры и . Траектории системы
(3.6) не покидают положительного орта. Пусть , где
n1
x...xS ++= 0p
i
> 0q
i
>
0c...cc
n21
≥≥≥> 0)c(f
ii
=
для всех . Представляет интерес проблема нахождения критерия
конкурентного отбора в данной модели.
n,...,1i =
Рассмотрим сначала случай
2n
=
. Точка
>
=
< 0,0,/,
1111
qpccr
- одно из
положений равновесия модели (3.6
). Оказывается непрерывная функция:
}p/qs,x,p/qsc,xcmax{L
2222111111
−
−
=
(3.7)
строго убывает на траекториях системы (3.6). Поэтому справедливо
Утверждение 2.7.
При
2n
=
в модели (3.6) равновесие
r
глобально
устойчиво при любых допустимых параметрах и .
}p{
i
}q{
i
В результате компьютерных экспериментов, установлено, что и при других
в конкурентном семействе биологических комплексов побеждает
субпопуляция с наибольшей потенциальной численностью. Справедливо простое
3n ≥
}s,x{
ii
Утверждение 2.8.
В модели (3.6) равновесие >
=
< 0,0,...,0,0,q/pc,cr
1111
локально устойчиво при любых допустимых параметрах и .
}p{
i
}q{
i
Здесь обоснование опирается на следующую Ляпуновскую функцию
}p/qs,x,...,p/qs,x,
1n
p/qsc
,
1n
xc
max{L
nnnn2222
111111
−
−
−
−
=
, (3.8)
убывающую на траекториях (3.6) из малой окрестности
r
.
Более естественной представляется другая версия обобщения (3.7):
)}/,max(...)/,max(
,/,max{
2222
111111
nnnn
pqsxpqsx
pqscxcL
++
−−=
(3.9)
После проведения многочисленных экспериментов с разными моделями
весьма правдоподобной представляется
Гипотеза.
Непрерывная функция (3.9) строго убывает на решениях (3.6).

52
Разумеется, если эта гипотеза верна, то отсюда вытекает глобальная
устойчивость данного равновесия
r
.
Обсуждение.
Для
непрерывных моделей данной главы был использован богатый набор
функций Ляпунова, опирающихся на операцию
max. Для дискретных
динамических систем, описывающих попарный обмен, загадочную эффективность
демонстрируют функция “сумма квадратов” и “число 3”. В этой связи, приведем
ряд задач из журнала “Квант“ (Ильичев, 1985, 1984, 2001б).
Задача М914.
На острове Серобуромалин обитают 13 серых, 15 бурых и 17
малиновых хамелеонов. Если встречаются два хамелеона разного цвета, то они
одновременно меняют свой цвет на третий (серый и бурый становятся оба
малиновыми и так далее). Может ли случится так, что через некоторое все
хамелеоны будут одного цвета ?
Решение. Пусть - вектор, характеризующий количество серых,
бурых и малиновых хамелеонов в момент времени . Очевидный закон сохранения
никак не помогает решению
. К счастью, здесь существуют и более
тонкие инварианты. Так, пусть - остаток от деления на 3 числа
),,(
ttt
mbs
t
45=++
ttt
mbs
t
r
tt
bs −
.
Переменная может принимать лишь три значения – это 0,1,2. Самое главное,
значение не меняется во времени при любых встречах хамелеонов. Если бы в
момент времени все ящерицы стали одного цвета, то . Но в начальный
момент времени имеет место
t
r
t
r
T
0=
T
r
2
0
=
r . Противоречие.
Задача М870. По одной стороне бесконечного коридора расположено
бесконечное число комнат, занумерованных целыми числами, и в каждой стоит по
роялю. В этих комнатах живет конечное число пианистов (в одной комнате
может жить и несколько пианистов) . Каждый день какие-то два пианиста,
живущие в соседних комнатах - -й и
k
)1(
+
k
-й - решают, что они мешают друг
другу, и переселяются в
)1(
−
k
-ю и
)2(
+
k
-ю комнаты. Докажите, что через
конечное число дней переселения прекратятся.
Решение. Обозначим через - номер комнаты , в которой проживает -й
пианист в момент времени . Здесь имеются два тривиальных (и бесполезных)
t
i
N
i
t
53
инварианта:
p
- общее число пианистов и
∑
=
p
i
t
i
N
1
- сумма номеров комнат, занятых
пианистами. Приведем два более полезных свойства.
1. Назовем блоком набор из 3 комнат с номерами , ,
m
B
1−m m 1
+
m
. Пусть
в некоторый момент времени в блоке находился хотя бы один пианист, тогда
и во все последующие времена там будет обитать некоторый пианист.
Следовательно, набор комнат, в которых побывает хотя бы один пианист конечно.
m
B
2. Рассмотрим следующую функцию состояния . Легко
убедится, что после каждого расселения функция возрастает.
∑
=
=
p
i
t
i
t
NQ
1
2
)(
Q
Теперь все готово, чтобы решить задачу. Предположим противное:
переселения продолжаются бесконечно долго. Тогда с учетом свойства 1 время от
времени должны возникать одинаковые состояния в распределении пианистов по
комнатам. Но появлению циклов препятствует свойство 2. Противоречие.
М1758.
Всякий депутат имеет свой (абсолютный) рейтинг. После избрания
каждый из них вошел в одну из фракций, в которой он может подсчитать свой
относительный рейтинг. Депутат переходит из одной фракции в другую, если его
относительный рейтинг увеличивается. Пусть в единицу времени может
происходить лишь один переход. Докажите, что спустя конечное время все
переходы прекратятся.
Решение. Обозначим: - абсолютный рейтинг -го депутата; - сумму
рейтингов всех депутатов, входящих в -тую фракцию в момент . Условие
“перехода” перехода -го депутата из -той фракции в -тую означает, что
выполняется неравенство
k
R
k
)(tS
i
i
t
i
n m
)](/[)(/ tSRRtSR
miini
+
<
. Это эквивалентно следующему
0)()(
<
−
+
tStSR
nmi
.
Отметим, что здесь получаем
inn
RtStS
−
=
+
)()1( и
imm
RtStS +=
+
)()1( .
Теперь рассмотрим функцию
∑
= )()(
2
tStL
j
, где индекс
j
пробегает все
номера фракций. Сравним значения
L
до и после перехода. Имеет место:
)()]()([2)()1( tLtStSRRtLtL
nmii
<
−
+
+
=+ .
Заметим, что
L
может принимать лишь конечное число значений, поэтому
убывание данной функции не может продолжаться сколь угодно долго.
54
2.4.
Приложение. Обоснование основных результатов.
Доказательство утверждения 2.1. Рассмотрим сначала “хорошие” точки
, в которых
)s,x(
p/sqxxx −≠−
**
. В этом случае функция из (1.4)
дифференцируема. Покажем, что она строго убывает. Возможны варианты:
L
1. Поэтому имеют место и . Значит,
( и . Следовательно, получаем
.xxL
*
−= 0xx
*
>−
p/sqxxx
**
−>−
*
xx <
)0)x(f >⇒
0sqpx >+−
0]qspx)x(xf[xL <+−−=−=
&
&
.
2. Значит, имеют место противоположные неравенства
.xxL
*
−=
0)x(f
<
и
. Отсюда находим .
0sqpx <+−
0xL <=
&
&
3. Поэтому . Значит,
.p/sqxL
*
−=
xxpsqx −>−
**
/
0sqpx >
−
.
Следовательно, получаем .
0][/ <+−=−= qspxsqpL
&
&
4. Действуя аналогично предыдущему варианту,
устанавливаем .
.xp/sqL
*
−=
0/ <= pqsL
&
&
Осталось проанализировать “плохие” точки, в которых функция
L может
быть
не дифференцируемой. Когда “плохая” точка отлична от равновесия
r
, то
возможны лишь следующие два варианта:
1+3. . Здесь 0p/sqxxxL
**
>−=−=
0
x
>
&
и
0
s
=
&
. Значит, в “следующее
мгновение” приведенное соотношение разрушается и реализуется случай 3.
Поэтому убывает.
L
1+4. . Отсюда следует , и значит,
. Поэтому получаем
0xp/sqxxL
**
>−=−= xxp/sq
*
>>
0qspx >+−
0
x
>
&
и
0
s
<
&
. Следовательно, убывает.
L
Осталось показать, что она стремится к нулю. Для этого воспользуемся так
называемой
"процедурой проталкивания предельной точки". Предположим
противное: для некоторой траектории
0A)t(L >→
>
=
< )t(s),t(x)t(Z системы
(1.3). Пусть
*
Z
- одна из предельных точек данной траектории, т.е. для
некоторой бесконечно возрастающей последовательности . Хотя таких
точек может быть много, но в каждой из них функция равна
*
k
Z)t(Z →
∞→}t{
k
L
A
.

55
Теперь рассмотрим новую траекторию , выходящую из точки
. Оценим значение
)t(Y
)0(YZ
*
=
)](Y[LB
τ
=
для малых
0>
τ
.
С одной стороны, убывает на траекториях (1.3), и поэтому
L
A
B < .
С другой стороны, оператор сдвига
)t(Z)t(Z:P
τ
+→
является
непрерывным, поэтому точку
)(Y
τ
можно трактовать как предел
последовательности
)}t(Z{
k
τ
+ . Поэтому
)(Y
τ
- одна из предельных точек данной
траекторий, и тогда
A
B
= . Противоречие. Окончательно, получаем
0
L
→
.
Идея доказательства утверждения 2.4 (Ильичев, 1995в). После
подстановки в (1.7) частного решения
(
)
ztx exp
=
получаем уравнение
()()
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−−++=
∫
∞
0
1exp dttmztpibaz (П.1)
При
1>ab
выберем
p
, удовлетворяющее одновременно неравенствам:
(
)
abapa 2
22
+<<
(П.2)
Далее, в области (см. приложение 5 главы 1) рассмотрим две функции
+
R
D
() ( )
ibpazzf
−
−
−=
и .
() ( ) ()
dttmztpzg
∫
∞
−=
0
exp
Очевидно, уравнение
()
(
)
0
=
+ zgzf
эквивалентно (П.1). Функция не имеет в
корней, поскольку
()
zf
+
R
D
0
<
− pa
(см. (П.2)). При больших
σ
на границе
выполняется
неравенство
+
R
D
gf >
. Тогда согласно теореме Руше в области
функции и будут иметь одинаковое число корней. Следовательно,
уравнение (П.1) будет устойчиво.
+
R
D
f gf +
Идея доказательства утверждения 2.5. Гладкая непрерывная система
(1.13) индуцирует гладкое сдвиг-отображение за период
T
(=отображение
Пуанкаре):
→)s,x(:P
00
)s,x(
TT
.
Обозначим через - начало и конец положительного,
)s,x(C
***
=
T
-
периодического решения (1.13). Очевидно, .
**
C)C(P =
Положим и
)s,x(Ax
00T
= )s,x(Bs
00T
=
. Покажем, что эти функции строго
возрастают по каждой переменной. Иными словами, матрица

56
(П.3)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
/
s
/
x
/
s
/
x
BB
AA
DP
состоит из положительных элементов для всех
x
и
s
.
Для этого воспользуемся принципом наследования локальных свойств,
изложенным в главе 4. Так, построим линейное локальное отображение,
индуцированное системой (1. 13):
],[
],)([
tttht
ttttht
qspxhss
qspxxFhxx
−+=
+−+=
+
+
(П.4)
где
),x(xf)x(F
θ
=
. Дифференциал отображения (П.4) в точке
),x(
θ
имеет вид
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−+
=
hqhp
hqpxFh
DL
x
1
])([1
/
. (П.5)
Имеет место следующее свойство: матрица
D
L - положительна при достаточно
малом . Согласно принципу наследования свойства матрицы
0h >
D
L
“передаются” матрице
D
P
, если они удовлетворяют требованиям (см. глава 4):
локальная универсальность, семейство всех образуют полугруппу, условие
грубости. Здесь эти требования выполняются, поэтому матрица (П.3) оказывается
положительной.
}DL{
Теперь на точках определим отношение полупорядка . А именно,
для точек и
)s,x(V =
)s,x(C
111
= )s,x(C
222
=
положим , если и
21
CC p
21
xx <
21
ss
<
.
Так как матрица
D
P
положительна, то отображение
P
сохраняет данное
отношение полупорядка. Формально, из следует .
21
CC p )C(P)C(P
21
p
Пусть . Рассмотрим так называемый конусный отрезок
21
CC p
}CVCV{)C,C(K
2121
pp
=
.
Геометрически, конусный отрезок представляет собой внутренность
прямоугольника, в котором самая слабая точка (
m
) является юго-западной
вершиной, а самая сильная точка (
M
) – это северо-восточная вершина. При
действии
P
конус переходит в некоторую криволинейную область,
вложенную в .
)C,C(K
21
)]C(P),C(P[K
21
Построим однопараметрическое семейство конусных отрезков (рис. 2.2)
}/CVCV{)(k
**
γγγ
pp= ,
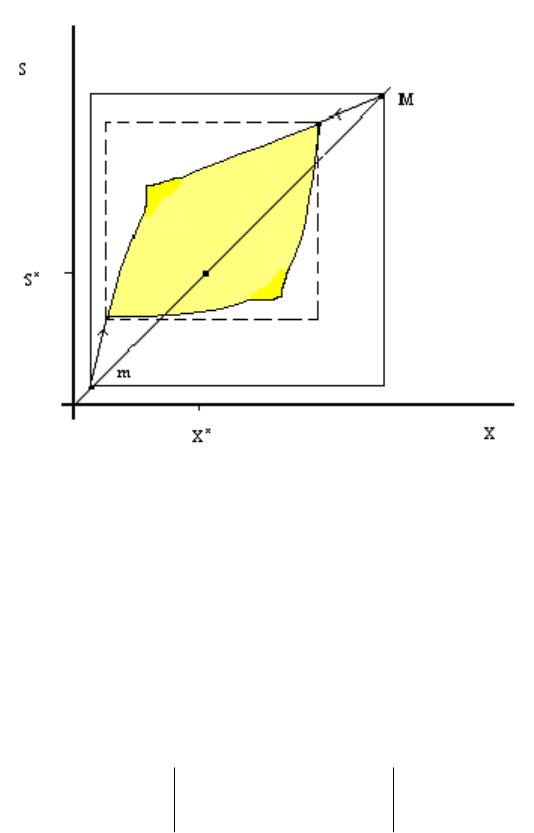
57
где параметр
γ
изменяется в . Очевидно, при
)1,0(
*
C)(k →
γ
1→
γ
, конусные
отрезки вложены друг в друга и при
2
R)(k
+
→
γ
0→
γ
. Для всякого
)(k
γ
имеют
место и . При говорят, что точка идет вперед, а
при говорят, что точка
*
Cm
γ
=
γ
/CM
*
=
)m(Pm p
m
M)M(P p
M
идет назад. Справедлива (Ильичев, 2008)
Лемма П.1.
Под действием
P
вершина идет вперед, а
m
M
идет назад.
Отсюда следует, что под действием
P
больший конусный отрезок
переходит в меньший. Теперь, применяя процедуру проталкивания предельной
точки, устанавливаем глобальную устойчивость .
*
C
Рис. 2.2.
Образ прямоугольника (заштрихован) под действием отображения
Пуанкаре.
Идея доказательства утверждения 2.6.
Обозначим через )(
i
pP
=
и
- диагональные матрицы. Тогда характеристическое уравнение для
системы (2.2) имеет вид:
)(
i
qQ =
()
0=
−−
−−
=
zEQP
QzEPA
zH
Назовем матрицу устойчивой, если все ее корни находятся в левой
комплексной полуплоскости (ЛКП). Обозначим
(
PA −
)
(
)
21
, ppd определитель матрицы
. Очевидно,
.
(
PA −
)
()
dd =0,0
Лемма П. 2.
Пусть и существуют такие параметры и , при 0>d
1
p
2
p
