Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.

198
интерпретировать как некоторую ценную бумагу, стоимость которой определяется
количеством рыбы в водоеме. При этом максимальный доход от этой ценной бумаги за
бесконечное время равен B (x), если x – начальная биомасса рыбной популяции. Иными
словами, с точки зрения владельца экосистемы (государства), B (x) – ее стоимость,
когда биомасса рыбы равна x. В этой связи договорные взаимоотношения владельца и
арендатора экосистемы («рыбака») на промежутке [t, t +1] могут основываться на
следующих соображениях:
А. В момент t государство продает рыбаку всю экосистему по цене B (x
t
). Как
правило, B (x
t
) велико и рыбак вынужден взять в банке ссуду в размере B (x
t
). Через год
он возвращает ссуду с процентами, т. е. B (x
t
)/
β
.
В. После годичной эксплуатации государство обратно выкупает всю экосистему
по цене B(x
t+1
).
С. Кроме того, рыбак еще получает доход от выловленной рыбы. Будем
предполагать, что в момент t происходит вылов и продажа рыбы. Вырученные деньги
p(u
t
) сразу кладутся в банк, поэтому в момент t+1 рыбак получит p (u
t
)/
β
.
В результате трех указанных операций прибыль рыбака в момент времени t+1
составляет
β
β
/)()(/)(),(
1 ttttt
upxBxBuxП
+
+
−
=
+
,
и ему приходится решать знакомую оптимизационную задачу:
)}()()(max{
1 tt
xBxBup
−
+
+
β
, по всем 0≤u≤x
t
,
где x
t+1
= f(x
t
- u). Из уравнения Беллмана следует, что П(x,u) ≤ 0 для 0 ≤ u ≤ x, причем
равенство достигается на оптимальном управлении u = u(x). Таким образом, рыбак
возвращает свои деньги, только если он ведет себя оптимально по отношению к
бесконечному горизонту. Разумеется, этот механизм является сугубо теоретическим,
так как никакой рыбак не согласится всего лишь на нулевую прибыль.
4. Когда производится водозабор из различных точек водоема, то внутренняя
цена воды может зависеть и от пространственной координаты. Так, будем считать,
что река представляет собой каскад шлюзов. Рассмотрим сначала модель одного
шлюза. Полагаем, что пока объем (или уровень) шлюза (
x
) меньше константы
M
вода из него не вытекает. А при возникает выходящий поток, равный
Mx >

199
)(
1
Mxkw −=
. Здесь - характеристика скорости вытекания (=пропускная
способность или вязкость),
1
k
10
1
<
<
k
. Для спокойной равнинной реки мало, а для
горной – относительно велико. Пусть задан входящий поток воды (
1
k
δ
), тогда
модель шлюза имеет вид:
, (О.1)
)()(
11 ttttt
xFMxkxx =−−+=
+
+
δ
здесь - так называемая неотрицательная разность.
Благодаря данной операции не возникает противотока воды из нижней части реки
в шлюз.
},0max{)( MxMx −=−
+
При
δ
δ
≡
t
график )(
1 tt
xFx
=
+
является кусочно-линейной, монотонно
возрастающей и строго вогнутой функцией. В модели (1) имеется единственное
положительное равновесие
1
*
k
Mx
δ
+=
, которое глобально устойчиво.
Далее, рассмотрим модель каскада двух шлюзов (
x
и
y
). Удобно считать,
что они составляют разбиение большого шлюза на два меньших. Тогда имеем:
)(
11 ttttt
yxkxx
−
−
+=
+
δ
= , (О.2) ),(
tt
yxf
+
+
−−−+= )()(
211
Mykyxkyy
ttttt
= , ),(
tt
yxg
где
x
и - объемы верхнего и нижнего шлюзов (или уровни при равенстве их
площадей). Кажется, что во избежание противотока (из нижнего шлюза в верхний)
в модели (О. 2) вместо линейного члена
y
)(
1 tt
yxk
−
лучше взять нелинейный член
. Для равнинных рек, где все
+
− )(
1 tt
yxk
5.0
<
i
k , в модели (О.2) реализуется
следующее примечательное свойство:
если , то и для всех
t .
00
yx ≥
tt
yx ≥
Поэтому при задании естественного начального условия можно при
формализации перетоков использовать линейные члены.
00
yx ≥
Пусть все
δ
δ
≡
t
, тогда в модели (О. 2) имеет место
21
kk
Mx
t
δ
δ
++→
и
2
k
My
t
δ
+→
при . ∞→t
200
Назовем отображение строго вогнутым в
mM
RRH →:
M
R
, если для любых
точек из
),( BA
M
R
и всякого числового параметра
λ
из справедливо
неравенство (в смысле открытого конуса )
]1,0[
m
R
+
)()()1(])1[( BHAHBAH
λ
λ
λ
λ
+
−
+
−
f
.
Легко видеть, что отображение (О. 2) является вогнутым в
2
R
.
Рассмотрим сначала водозабор из одного шлюза. Если - величина изъятия
воды, то потребуем, чтобы оставшийся объем был не меньше некоторой заданной
величины . В дальнейшем полагаем
u
1
N
MN
i
=
для всех . Поэтому управление
удовлетворяет условию
i
Mxu
−
≤
≤
0
. В этом случае получаем рекуррентное
соотношение
)}]({)(max[)(
1
uxFBupxB
tnn
−
+
=
+
β
по всем допустимым .
u
Здесь - функция полезности (монотонная и строго вогнутая);
p
β
- величина
дисконта, близкая к 1; - функция Беллмана (= макcимально возможный
доход за
n
лет); - функция (О.1).
)(xB
n
F
По индукции устанавливаем, что все - вогнутые функции при .
Разумеется, они являются и монотонно возрастающими. Последовательность
сходится к некоторой предельной функции , которая наследует
основные свойства – вогнутость и монотонность.
)(xB
n
1
Nx ≥
)}({ xB
n
)(xB
В результате компьютерных расчетов обнаружено, что управление равно
нулю при , а затем непрерывно возрастает. Кроме того, независимо от
начальных условий переменная
Mx ≤
x
в модели (О.1) с управлением стремится к
δ
+
1
M
.
При выполняется важное соотношение
Mx ≥
)()(
//
upxB = .
Величину можно считать (внутренней) ценой воды. Как зависит
внутренняя цена воды от проточности ( ) шлюза? Оказалось, что с ростом цена
воды уменьшается.
)(
/
xB
k k
Рассмотрим теперь водозабор из двух шлюзов. Пусть - водопотребление
из первого и второго шлюзов, соответственно. Считаем, что выполняются
vu,
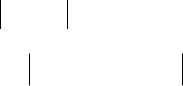
201
ограничения и
Mxu −≤≤0
Myv
−
≤
≤
0
. С учетом модели (О. 2) получаем
рекуррентное соотношение Беллмана
)}],(),,({)()(max[),(
1
vyuxgvyuxfBvqupyxB
ttttnn
−−
−
−
+
+
=
+
β
по всем допустим . Здесь - функции полезности (монотонные и строго
вогнутые). Легко показать, что все функции являются монотонно
возрастающими и вогнутыми. Последовательность данных функций также
сходится к некоторой монотонно возрастающей и вогнутой функции, а
соответствующие управления непрерывны.
),( vu qp,
),( yxB
n
Величину будем назвать внутренней ценой воды верхнего шлюза, а
),(
/
yxB
x
),(
/
yxB
y
- внутренней ценой воды нижнего шлюза. В результате численных
экспериментов обнаружено, что во многих случаях цена воды верхнего шлюза
выше цены воды нижнего шлюза. Такое соотношение внутренних цен доставляет
максимум при совместном водопотреблении.
Последнее. Сторонники принципа максимума Понтрягина часто пугают
остальных тем, что функция Беллмана не всегда дифференцируема. Однако во
многих задачах функция Беллмана является возрастающей по каждому из своих
аргументов, и тогда она имеет частные производные почти всюду….
7.6. Приложение. Обоснование основных результатов
Доказательство свойства 1. 1. Удобно ввести новую функцию z с более
широкой областью определения, чем функция s:
)u,x(s)u,x(z =
при
x
u ≤
и
)x,x(s)u,x(z
=
при
x
u > .
Очевидно, - непрерывна и S(x) = max z(x, u) по всем 0 ≤ u ≤x.
)u,x(z
Обозначим - какое – либо значение переменной , на котором достигается
максимум при фиксированном . Последовательность может быть сильно
колеблющейся и никуда не сходится. Тем не менее .
*
i
u u
),( uxz
i i
x
}{
*
i
u
),()(
*
iii
uxzxS =
Пусть заданы , сходящаяся последовательность и
0
x
0
}{ xx
i
→
0>
ε
. Покажем,
что при некотором
δ
из условия
δ
<−
i
xx
0
следует неравенство
ε
<
−
)x(S)x(S
i0
. (П.1)

202
Выберем достаточно большой компакт
}x2u0иx2x2/x:)u,x{(K
oo0
≤
≤
≤
≤
= ,
заведомо окружающий точки при всех достаточно больших
i
. Положим
для
),(
*
ii
ux
)u,x(A
iii
= 2,1i
=
и на
K
определим следующую метрику
212121
uuxxAA −+−=−
.
Из непрерывности вытекает ее равномерная непрерывность на K. Поэтому при
некотором из
z
*
δ
*
21
AA
δ
<− следует
ε
<
−
)A(z)A(z
21
. В частности, при
*
0
δ
<−
i
xx
имеет место
ε
<− ),(),(
*
0
*
00
uxzuxz
i
. (П.2)
С другой стороны, для промежуточного значения выполняется неравенство
),(
*
0
uxz
i
. (П.3)
),(),(
**
0 iii
uxzuxz ≤
Из (П.2) и (П.3) вытекает , что равносильно неравенству
ε
+< ),(),(
**
00 ii
uxzuxz
ε
+
<
)()(
0 i
xSxS . (П.4)
Теперь, используя другое промежуточное значение , устанавливаем
),(
*
0 i
uxz
ε
+
<
)()(
0
xSxS
i
. (П. 5)
Последние два неравенства эквивалентны (П.1).
Доказательство свойства 1.2. Ниже используем некоторые обозначения из
леммы 1. Рассмотрим произвольную сходящуюся последовательность . В
силу строгой вогнутости функции по переменной , каждое значение
находится однозначно. Для демонстрации непрерывности достаточно показать
.
0
}{ xx
i
→
),( uxs
i
u
*
i
u
)(xu
*
0
*
}{ uu
i
→
Очевидно, для всякого
i
выполняется строгое неравенство
. (П. 6)
),(),(
*
0
*
uxsuxs
iii
>
Последовательность ограничена. Поэтому существует подпоследовательность
сходящаяся к некоторому значению , здесь индекс пробегает некоторое
бесконечное подмножество натуральных чисел. Устремим к бесконечности, тогда
}{
*
i
u
}{
*
k
u
v k
k
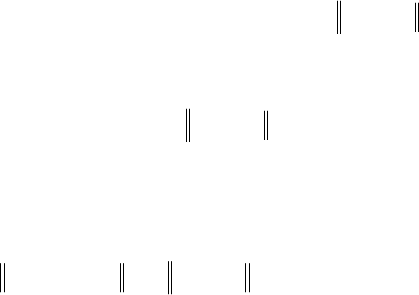
203
из (П. 6) получаем . С учетом строгой выпуклости функции по
находим .
),(),(
*
000
uxsvxs ≥
s u
*
0
uv =
Доказательство утверждения 1.1. Зафиксируем достаточно большое число
а так, чтобы из каждого неравенств 0 ≤ и ≤ х ≤ а следовало ѓ(х - и) ≤ а. На отрезке
[0, a] рассмотрим полное пространство (С) всех непрерывных функций с
чебышевской нормой
║g║= max│g(x)│ по всем 0 ≤ x ≤ a.
Далее, определим оператор А выражением по всем
0 ≤ u ≤ x.
)}()(max{)( uxgfupxAg
−
+
=
β
Согласно свойству 1.1 A(g)( x) – непрерывная функция, поэтому А отображает С в себя.
Покажем, что оператор А является сжатием. Возьмем две функции -
элементы пространства С. Имеют место соотношения
)(),(
21
xgxg
)}()(max{)(
iiii
uxfgupxAg
−
+
=
β
,
где - оптимальный вылов в точке
)(xuu
ii
=
x
;
2,1
=
i
. В частности, устанавливаем
)()()(
1111
uxfgupxAg
−
+
=
β
,
)()()(
1212
uxfgupxAg
−
+
≥
β
.
После вычитания этих соотношений
21121121
)]()([)()( gguxfguxfgxAgxAg −≤−−−≤−
ββ
.
Аналогично, используя управление
)(
22
xuu
=
, получаем
1212
)()( ggxAgxAg −≤−
β
.
Поскольку эти неравенства годятся для любого
x
из , то с учетом последних
неравенств получаем условия сжатия
],0[ a
1221
ggAgAg −≤−
β
.
В силу принципа сжимающих отображений, в С существует единственная неподвижная
точка оператора А, которая и совпадает с решением уравнения Беллмана на отрезке [0,
a]. Поскольку а можно выбрать сколь угодно большим, то данная задача однозначно
разрешима на всей полуоси [0, + ∞ )
Доказательство леммы 1.1. Предположим противное: при некотором
0
x
>
оптимальный вылов . Поэтому
x)x(u =
204
)x(p)x(B
=
.
Рассмотрим допустимую последовательность выловов:
ε
−
=
xu
0
и
)(
1
ε
Fu = при малом
0>
ε
; 0u
t
=
для остальных
2
t
≥
. Здесь возникает доход
))(()()(
ε
β
ε
ε
FpxpD
+
−
=
.
Очевидно, и . Поскольку и
, то . Значит,
)x(p)0(D =
)()0()0(
///
xpFD −=
β
1)0(
/
>F
β
1)x(p
/
< 0)0(D
/
>
)x(B)(D >
ε
при малых
0>
ε
, но это
противоречит оптимальности приведенной ранее стратегии.
Доказательство утверждения 1.2. 1) Зафиксируем натуральное
k
и
обозначим через композицию
()
xF
k
k
штук отображений
F
. В точке
x
построим
следующую допустимую последовательность управлений: , а для
остальных . Тогда получаем
()
xFu
k
k
=
0=
m
u
(
)
(
)
[
]
xFpxB
kk
β
≥
. А поскольку
(
)
00
=
F , то
()
== 00B
()
[
]
0Fp
kk
β
. Значит, находим
()
(
)
(
)
[
]
(
)
[
]
{
}
00 FpxFpBxB
kkk
−
≥−
β
.
После деления на малое положительное
x
устанавливаем
() ()
[
]
()
000'
//
pFB
k
β
≥+ .
В силу условия и
1)0(
/
=p
(
)
10
/
>F
β
, поэтому правая часть неравенства больше
единицы. С ростом
k
правая часть стремится к бесконечности.
Доказательство утверждения 2.1. Отметим, что для вогнутых функций
всегда существуют производные как слева, так и справа. Поэтому следует лишь
установить совпадение их значений. Пусть - оптимальное управление в
начальной точке . Тогда выполняется равенство
u
0>x
(
)
(
)
(
)
[
]
uxFBupxB
−
+
=
β
. (П.7)
Рассмотрим точку
ε
+=
x
y
, где
0>
ε
. Определим допустимую последовательность
управлений
{
, выходящую из точки :
}
t
v
y
xyuv
−
+
=
00
и
tt
uv
=
для 1≥
t
.
Очевидно, для
tt
xy =
1≥
t
. Поэтому для
ε
+
=
x
y
выполняется оценка
()
(
)
(
)
(
)
uxFBupxB
−
+
+
≥
+
β
ε
ε
(П.8)
Вычитая из неравенства (П.8) соотношение (П.7), получаем
205
()
(
)
(
)
(
)
0
upupxBxB
−
+
≥
−
+
ε
ε
.
Разделим данное выражение на малое
ε
, тогда находим
(
)
(
)
upxB '0' ≥
+
(П.9)
Отметим, что данная оценка является универсальной при всех допустимых .
0
u
Приведем теперь специальную оценку для . Тогда при достаточно
малом
0>u
0>
ε
возникает аналогичная допустимая последовательность
{
}
t
v ,
выходящая из точки
x
x
y
<
−=
ε
. В этом случае получаем
(
)
(
)
(
)
(
)
ε
ε
−
−
≤
−
−
upupxBxB
.
Следовательно, находим
(
)
(
)
upxB '0'
≤
−
(П.10)
Но для всякой вогнутой функции имеет место неравенство
Поэтому из оценок (П.9) и (П.10) заключаем
()(
0'0' +≥− xBxB
)
.
()
(
)
1''
<
= upxB
.
Обратно, пусть выполняется соотношение (2.1). В данной точке
x
оптимальное управление (
v
) должно быть положительным, иначе .. Тогда
согласно предыдущему имеет место
1)(
/
≥xB
(
)
(
)
vpxB ''
=
. Из (2.1) следует .
uv =
Доказательство утверждения 2.2. Достаточно показать, что при малых
x
оптимальный вылов равен нулю. Обозначим через - набор оптимальных
выловов, соответствующих начальной точки . Если - мало, то
для всех из .
,...}u,u{
10
0
x
0
x
β
/1)(
/
>zF
z ]x,0[
0
Построим вторую допустимую последовательность выловов:
)ux(F)x(Fuv,0v
000110
−
−
+== и
tt
uv
=
для остальных
2
t
≥
.
Поскольку указанные выловы малы, то и
1010
v,v,u,u
tt
u)u(p ≈
tt
v)v(p
≈
для
1,0
t
= . Пусть
H
- разность доходов от первой (=оптимальной) и второй
стратегий. Тогда имеем
β
β
β
)]()([
00001010
xFuxFuvvuuH
−
−
+
=
−
−
+≈ .
Обсудим поведение функции при заданном . Очевидно, и
)(
0
uH
0
x
0)0(H =
0)(1)(
00
/
0
/
<−−= uxFuH
β
для всех из . Поэтому достигает максимума при .
0
u ]x,0[
0
)(
0
uH 0u
0
=
206
Идея доказательства утверждения 2.3. Первоначальное обоснование
приведено в работе (Ильичев, Рохлин, Угольницкий, 2000). Ниже изложим новое
доказательство, являющееся аналогом обоснования утверждения 2.1.. Для
удобства константу неприкосновенного запаса обозначим через . Положим
, тогда для всех имеем (=вылов во второй год
положителен). Пусть для такой точки
0
N
00
1
1
)( NNFN <=
−
1
Nx > 0
1
>u
x
задана последовательность оптимальных
выловов . Разумеется, каждый вылов непрерывно зависит от
,...},{
10
uu )(xu
k
x
.
Выпишем первые три точки данной орбиты , где
. Тогда имеет место соотношение
,...}),(,{
0
auxFx −
])([
10
uuxFFa −−=
. (П. 11)
)()()()(
2
10
aBupupxB
ββ
++=
Выберем малое число
ε
. Очевидно,
)(
1
ε
+
<
xN
. В точке
)(
ε
+x
построим
допустимую последовательность выловов , которая отличается от
предыдущей только на элементе
,...}
ˆ
,
ˆ
{
10
uu
δ
+
=
11
ˆ
uu
. Соответствующая траектория имеет
вид
),...})((),(,{
100
δ
ε
ε
ε
−
−
−
+
−++ uuxFFuxFx . Выберем
δ
так, чтобы новая
траектория также оказалась в точке
a
через два шага. Это возможно при
.
)()()(
0
/
00
uxFuxFuxF −≈−−−+=
εεδ
Далее, имеет место неравенство
. (П. 12)
)()()()(
2
10
aBupupxB
βδβε
+++≥+
Вычитая из соотношения (П. 12) равенство (П.11), получаем
. (П. 13)
εβδβε
)()()]()([)()(
0
/
1
/
11
uxFupupupxBxB −≈−+≥−+
Устремим положительное число
ε
к нулю, тогда из (П. 13) находим
KxB ≥+ )0(
/
,
где здесь и ниже .
)()(
0
/
1
/
uxFupK −=
β
А теперь устремим отрицательное число
ε
к нулю, тогда из (П. 13) находим
KxB ≤− )0(
/
,
Но для всякой вогнутой функции
B
выполняется неравенство . )0()0(
//
+≥− xBxB
Поэтому имеет место . Итак, если - элементы
оптимальной последовательности выловов в точке
KxBxB =+=− )0()0(
//
10
,uu
x
, то справедливо равенство
207
. (П.14)
)()()(
0
/
1
//
uxFupxB −=
β
Поскольку выражение справа – непрерывная функция, то
B
непрерывно
дифференцируема для .
1
Nx >
Данная процедура расширения области дифференцируемости
B
может быть
продолжена. Так, положим , тогда при оптимальный элемент
положителен. В результате “шевеления”
)(
1
1
−
−
=
kk
NFN
k
Nx >
k
u
x
и получаем формулу, в которой
выражается через произведение непрерывных функций и .
k
u
)(
/
xB
/
p
/
F
Последнее, набор сходится к нулю, значит - непрерывно
дифференцируемая функция для всех .
}{
k
N
)(xB
0>x
Идея доказательства утверждения 2.4. Для данная теорема,
очевидно, справедлива. Пусть теперь , тогда для оптимального вылова в
точке
Nx ≤
Nx >
x
имеет место . Кроме того, выполняется соотношение
xu <<0
(
)
(
)
(
)
[
]
uxFBupxB
−
+
=
β
.
Данный вылов является допустимым и для точки
ε
+
x
, когда
ε
достаточно
мало. Поэтому имеет место неравенство
(
)
(
)
(
)
[
]
uxFBupxB
−
+
+
≥
+
ε
β
ε
.
Далее, действуя как в обосновании утверждения 2.1, получаем соотношение
(
)
))(()(
///
wFBwFxB
β
= ,
где
u
x
w −=
. В последнем равенстве слева находится убывающая функция
x
, а
справа – убывающая функция . Отсюда получаем: возрастает по
w w
x
, что и
требовалось доказать.
Идея доказательство утверждения 2.5. Ниже понадобится
Свойство П.1. Для всех х>0 имеет место
(
)
(
)
xBxp ''
<
.
Обоснование свойства П.1. При
N
x
≤
<
0 имеет место и при всех
имеет место . Значит,
()
1' ≥xB
0>x
()
1' <xp
(
)
(
)
xBxp ''
<
.
Пусть теперь
N
x
> . Согласно лемме 1.1 при всех 0>
x
имеем
x
u
<
. С
учетом (2.1) и строгого убывания
'
p
получаем
(
)
(
)(
xpupxB ''' >
)
=
. Свойство П.1
доказано.
Далее, обозначим
()
(
)
(
)
xuBupu '
−
=
Φ
. Очевидно, - вогнута. При
()
uΦ
