Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.

178
можно построить схему налогообложения рыбаков, которая снимает все
противоречия.
В процессе длительной эксплуатации нарушается равновесие в экосистеме, и
в качестве ответной адаптивной реакции популяции изменяют свои параметры.
Например, сокращение размера рыб снижает возможности их вылова, хотя это
одновременно и уменьшает их конкурентоспособность. Поэтому при заданном
режиме эксплуатации реализуется некоторый "компромиссный" вариант значений
биологических параметров (размер, возраст, подвижность и т.д.) популяций. В этой
связи представляет интерес следующая проблема.
Проблема 3. Как в процессе адаптации изменяются внутренние цены
эксплуатируемых популяций?
Решение данной проблемы определяет возможные тенденции в стратегии
налогообложения на перспективу. В целом анализу приведенных проблем
посвящена данная глава.
7.1. Концепция внутренней цены для эксплуатируемой популяции
Пусть x -биомасса всей рыбной популяции, тогда с учетом вылова
(
)
u
динамика биомассы (в кг) представляется в дискретной форме
(
)
ttt
uxFx
−
=
+1
(1.1)
где
t
- номер года;
F
- непрерывно дифференцируемая функция
воспроизводства; ;
()
00 =F
tt
xu
≤
≤
0
для всех
t
.
Обозначим через функцию полезности "рыбака" от продажи (кг)
рыбы в момент времени
(
t
up
)
t
u
t
. Считаем, что функция
p
строго возрастает, строго
вогнута (выпукла вверх), непрерывно дифференцируема;
()
00
=
p
. Без
ограничения общности положим
(
)
10'
=
p
. Такая функция
p
всегда допускает
представление
() ()
uuup
ϕ
=
. Убывающая функция
(
)
u
ϕ
является средней
рыночной ценой единицы веса рыбы.
Более тонкое определение цены дается в теории полезности (Зангвилл, 1973).
Так принято считать: - это цена единицы рыбной продукции, когда общее
()
up'
179
предложение рыбы на рынке равно . Здесь после проданных u
ε
(кг) рыбы цена
увеличивается и равна
()
ε
−
up'
. Такая формализация соответствует известной
экономической закономерности: чем меньше предложение товара, тем выше его
цена. Поэтому является максимальной рыночной ценой единицы рыбной
продукции.
()
10' =p
Как правило, в моделях динамики и эксплуатации биоресурсов выбирают
линейную функцию полезности
(
)
uup
=
(Скалецкая, Фрисман, Шапиро, 1979).
Однако существенно более содержательная теория ("оптимизация + экономическая
начинка") возникает при нелинейной функции полезности (см. ниже).
Основная задача управления заключается в максимизации дисконтированного
(дисконт
10 <<
β
) дохода за
T
шагов:
. (1.2)
()
t
T
t
t
up
β
∑
=0
Пусть
x
- начальное значение биомассы популяции, тогда через
(
)
xB
T
обозначим максимум (точнее, супремум) величины (1.2). Так из (1.2)
непосредственно находим
(
)
(
)
xpxB
=
0
. Далее, на основе методов динамического
программирования получаем рекуррентное соотношение Р. Беллмана (1960):
()
(
)
(
)
(
)
[
]
uxFBupxB
TT
−
+
=
−1
max
β
по всем из . u
[]
x,0
В монографии (Ланкастер, 1972) приведены полезные свойства,
характеризующие ”непрерывные” свойства оператора . Ниже в несколько
упрощенной формулировке приведены два из них.
max
Свойство 1. 1. Пусть s = s(x, u) – непрерывная функция двух переменных, тогда
и функция
S(x) = max s(x, u) по всем 0 ≤ u ≤x
является непрерывной.
Отсюда, используя индукцию по , заключаем: каждая - непрерывная
функция
T
()
xB
T
x
. Приведем основные характеристики функций Беллмана.
Функция строго возрастает по
)x(B
T
x
. В самом деле, пусть -
оптимальный набор вылов, соответствующий начальной биомассе рыбной
}u{
t
180
популяции
x
. Для при
y
y
x
<
определим допустимую последовательность , в
которой и для всех
}v{
t
00
uxyv +−=
tt
uv =
1
t
≥
. Тогда, очевидно, имеет место
∑
T
t
t
up
0
)(
β
t
T
t
vp
β
∑
<
0
)(
.
Значит, для оптимального набора выловов, соответствующего
y
, выполняется
неравенство .
)y(B)x(B
TT
<
Функция строго вогнута по
)x(B
T
x
. Применим индукцию по
T
. Для
0
T
=
имеем и, значит, вогнута по )x(p)x(B
0
= )x(B
0
x
. Пусть вогнута (в
силу свойства монотонности, она и возрастает). Множество всех возрастающих и
одновременно строго вогнутых функций замкнуто относительно операции
композиции, поэтому - строго вогнута.
1T
B
−
FBH
1T
o
−
=
Пусть и - оптимальные выловы, соответствующие начальным
u v
x
и
y
.
Очевидно, вылов
vuw
μ
λ
+=
является допустимым для начальной точки
y
x
z
μ
λ
+=
. С учетом строгой вогнутости
p
, имеет место оценка
)]()([)()()()()( vyHuxHvpupwzHwpzB
T
−+
−
+
+
>
−
+≥
μ
λ
β
μ
λ
γ
.
Отсюда получаем основное условие выпуклости
)y(B)x(B)z(B
TTT
μ
λ
+> .
Таким образом, свойства монотонности и вогнутости исходных функций
F
и “наследуются” функцией Беллмана.
p
Оптимальный набор вылов на участке
]
1
T
,0
[
−
является, очевидно,
допустимым и на отрезке
]
T
,0
[
. Поэтому )x(B)x(B
T1T
≤
−
для всех
0
x
≥
.
При заданной функции оптимальный вылов доставляет максимум
функции
1T
B
− T
u
() ( )(
[
uxFBup
T
−+
−1
)
]
β
. Эта функция непрерывна по обеим переменным и
строго вогнута по
u
.
Имеет место
Свойство 1.2. Пусть s = s(x, u) – непрерывна по обеим переменным, а также
дополнительно строго вогнута по переменной
u
, тогда функция
u(x) = arg max s(x, u) по всем 0≤ u ≤ x
является непрерывной.
Поэтому в данной задаче оптимальный вылов непрерывно зависит от
T
u
x
.
181
При конечном периоде эксплуатации возникает следующее печальное
обстоятельство - необходимость вылова всей популяции в последний год. Во
избежание этого целесообразно рассмотреть задачу (1.2) при бесконечном периоде
промысла (
∞=
T
):
. (1.3)
()
sup
0
→
∑
∞
=
t
t
t
up
β
Обозначим через предел последовательности при
)x(B
)}x(B{
T
∞
→
T
.
Оказывается, этот предел существует и является непрерывной, возрастающей и
вогнутой функцией. Она удовлетворяет так называемому уравнению Беллмана
))](()(max[)( uxFBupxB
−
+=
β
по всем из
u
]
x
,0
[
.
С экономической точки зрения, B(x) - это максимально возможный доход,
который можно получить от эксплуатации рыбной популяции. По сути, B(x) -
стоимость рыбной популяции, когда ее численность равна x. Данная интерпретация
будет использована при построении экономических механизмов управления
рыбным промыслом.
Как и ранее, оптимальный вылов является непрерывной функцией.
)x(u
Лемма 1.1. Если , то для оптимального вылова выполняется
неравенство
β
/1)0(
/
>F
u (x) <x при всех x> 0.
Таким образом, при оптимальном вылове, рассчитанном на бесконечный
период, популяция не уничтожается (по крайней мере, за конечное время).
В работе (Ильичев, Рохлин, Угольницкий, 2000) было получено решение
задачи (1.1)+(1.3) для следующего класса функций воспроизводства:
F
непрерывно дифференцируема, возрастает и вогнута: , и
при больших
()
00 =F
()
β
/10
/
>F
()
1/ <xxF
x
. Например,
(
)
(
)
xxxF
+
=
β
/2
,
() ( )
xxF += 2/ln
β
и т.д.
Справедлив следующий результат
Утверждение 1.1. Уравнение Беллмана имеет единственное решение В(х),
которое является непрерывной функцией.
Разумеется, функция строго возрастает и строго вогнута.
)(xB
182
Данные свойства во многом переносятся и на другие классы функций
воспроизводства. Так, рассмотрим специальный класс унимодальных (т.е.
имеющих глобальный максимум в некоторой единственной точке
0
*
>
x
)
непрерывно дифференцируемых функций
(
)
xF . Самое главное, предполагаем, что
в графике
F
левая ветвь (т.е. при
*
0
x
x
≤
≤
) вогнута; и
()
00 =F
(
)
β
/10' >F
.
Например, зависимость Риккера (1954)
(
)
(
)
xAxxF
−
=
exp
при
β
/1>A
является
такой функцией. Разумеется, прежний класс монотонных и вогнутых функций
воспроизводства также описывается данной схемой, если положить
∞
=
*
x
.
Сведение задачи управления с унимодальной функцией воспроизводства к
прежней достигается следующим образом. А именно, построим новую функцию
воспроизводства (=”выпрямление” F):
(
)
(
)
yFxG max
=
по всем из y
[
]
x,0
.
Здесь
()
)(xFxG
=
и строго возрастает при
*
x
x
≤
;
(
)
(
)
*
xFxG = при всех
*
x
x
>
;
вогнута и непрерывно дифференцируема;
(
)
00
=
G
и
()
β
/10' >G
. Значит,
G
принадлежит к уже изученному классу функций воспроизводства.
В этой связи рассмотрим новую модель динамики и эксплуатации рыбной
популяции в новой модели:
(
)
ttt
vxGx
−
=
+1
, (1.4)
в которой принадлежит [0, ] для всех t. А оптимальная последовательность
выловов
{
определяется из прежнего критерия:
t
v
t
x
}
t
v
()
→
∑
∞
=
t
t
t
vp
β
0
sup. (1.5)
Поскольку , то с помощью новой модели можно достичь не
меньшего значения целевой функции, чем с помощью старой модели (1.1). Теперь
заметим, что для каждого оптимального вылов имеет место .
Поэтому здесь «работает» только левая ветвь графика функции воспроизводства
. Последнее, левые ветви
)()( xFxG ≥
t
v
*
xvx
tt
≤−
G
F
и
G
совпадают, значит, совпадают их
оптимальные выловы и орбиты.
183
Предложение 1.1. Для всех x имеем u(х)=v(х), и при равенстве начальных
условий модели (1.1) и (1.4) порождают одну и ту же траекторию.
Следовательно, задача (1.1) + (1.3) и задача (1.4) + (1.5) эквивалентны.
Утверждение 1.2. При имеет место
β
/1)0(
/
>F
(
)
∞=
+
0'B
В силу вогнутости
(
)
xB график
(
)
xB' напоминает убывающую кривую
спроса в экономике (рис. 7.1): чем больше объем «товара»
x
, тем меньше его цена
. Величину будем называть внутренней ценой единицы биомассы
популяции, когда ее биомасса равна
()
xB'
()
xB'
x
. Согласно утверждению 1.2, данная цена
стремится к бесконечности, когда численность популяции стремится к нулю.
Разумеется, внутренняя цена определена только для эксплуатируемых популяций.
Ниже будем придерживаться прежних ограничений на модельные функции
p
и
F
. Напомним их: функции и F
p
строго возрастают, строго вогнуты,
непрерывно дифференцируемы;
(
)
00
=
p
и
(
)
10'
=
p
;
(
)
00
=
F
и
()
β
/10' >F
.
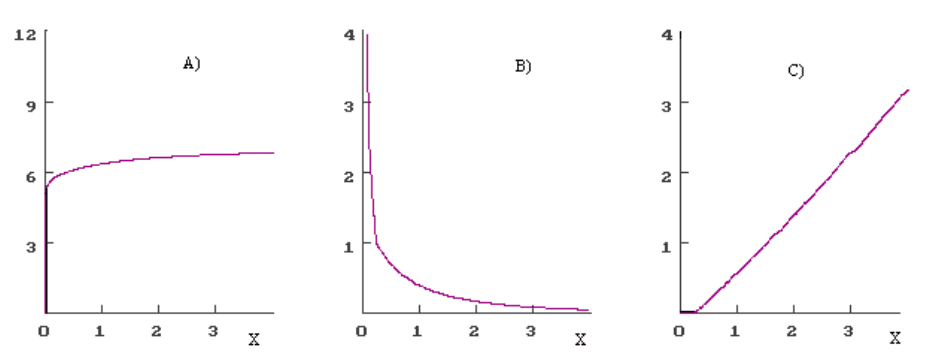
Рис. 7.1. Функция Беллмана – А; внутренняя цена -B; оптимальный вылов – С.
7.2. “Волшебная сила“ внутренних цен:
от глобальной оптимизации к локальной
В теоретическом и прикладном аспекте важную роль играет взаимосвязь
функции Беллмана и оптимального управления.
184
Утверждение 2.1. Для положительного оптимального управления
(
)
xuu
=
выполняется равенство
(
)
(
)
1
//
<= upxB (2.1)
Обратно, пусть имеет место соотношение (2.1), тогда
u - положительное
оптимальное управление в точке х.
Пусть в точке вылов положителен. Функция непрерывна и, значит
вылов положителен и в некоторой окрестности . Так как здесь убывает,
то в силу (2.1), функция возрастает. Далее, будет возрастать и при
всех . Отсюда (с учетом приложения) получаем классический результат
(Абакумов, 1994)
0
x
)x(u
0
x
)x(B
/
)x(u )x(u
0
xx >
Утверждение 2. 2. Оптимальный вылов имеет вид:
u
(x)=0 для x≤N и (x) возрастает при N> x,
u
где N –некоторая положительная константа ("неприкосновенный запас").
Следовательно, при малой численности рыб нецелесообразно производить
промысел. На практике этим обстоятельством, зачастую, пренебрегают.
Предыдущую теорему дополняет следующее
Утверждение 2. 3. Функция
(
)
xux
−
строго возрастает по переменной
x
.
Иными словами, оптимальный вылов медленно возрастающая функция.
Из двух теорем 2.1 и 2.2 вытекает, - непрерывно дифференцируема
при . Оказывается, справедливо большее (Рохлин, 2000)
)(xB
Nx >
Утверждение 2. 4. Функция - непрерывно дифференцируема при всех
.
)(xB
0>x
В силу непрерывности функции
(
)
xB' , из (2.1) следует для
()
1' =NB
N
-
«неприкосновенного запаса». Поскольку
(
)
xB' - убывающая функция, то при
N
x
< внутренняя цена больше единицы и, значит, выше рыночной (рис. 7.1).
На основе формулы (2.1) построим корректный экономический механизм
взаимоотношений «государства» и «рыбака». А именно, если в момент
t
«рыбак»
выловил (кг) рыбы, то он должен заплатить «государству» налог в размере
. С другой стороны, после продажи этой рыбы на рынке «рыбак» получит
t
u
(
tt
xBu '
)
185
доход . Поэтому максимизация ежегодной ( т.е. в интервале ) прибыли
«рыбаком» опирается на решение локальной задачи:
(
t
up
)
][
1, +tt
max по всем из
()
[]
ttt
cuup −
t
u
[
]
t
x,0 , (2.2)
где для всех
()
t
xBc '=
t
. Справедливо
Утверждение 2. 5. Решение в локальной задаче совпадает с оптимальным
управлением в глобальной задаче (1.1)+(1.3).
Таким образом, найденное управление в локальной статической задаче (2.2)
в точности совпадает с управлением в глобальной динамической задаче (1.3).
Отметим, что в прежней (нерыночной) системе государство само должно
было бы заняться максимизацией целевой функции (1.3). Теперь же государство
«перепоручает» реализацию оптимального промысла рыбаку. Грубо говоря,
государство «ловит рыбу чужими руками». За это оно вынуждено поступиться
частью своего дохода, Более формально выпишем доходы государства
(
)
G и
рыбака
(
за весь период эксплуатации:
)
R
t
t
t
t
cuG
β
∑
∞
=
=
0
и ,
()
[]
t
t
ttt
cuupR
β
∑
∞
=
−=
0
где для всех
()
tt
xBc '=
t
. Тогда целевая функция (1.3) означает, что
«спровоцированный государством» набор управлений призван
максимизировать суммарный доход
{}
t
u
(
)
RG
+
.
Далее, если вылов не производится, то динамика биомассы рыбной
популяции описывается уравнением
(
)
tt
xFx
=
+1
. Если
F
- унимодальна, то
поведение может быть весьма разнообразным (вплоть до возникновения
хаотических режимов). Представляет интерес вопрос: насколько оптимальная
эксплуатация деформирует динамику популяции. Оказывается здесь оптимальное
управление стабилизирует динамику популяции. Так, обозначим
b - точку из
{}
t
x
[
]
*
,0 x , в которой . Справедливо
()
β
/1
/
=bF
Утверждение 2. 6. В модели оптимально эксплуатируемой популяции (1.1)
+ (1.3) равновесие глобально устойчиво в .
()
bF
+
R
186
Удивительно, что координата устойчивого равновесия в модели (1.1) +
(1.3) никак не зависит от функции полезности
()
bF
p
.
В данной (“мягкой“) схеме налогообложения предполагалось, что “рыбак”
руководствуется своими локальными экономическими интересами. Представляет
интерес вопрос о возможных изменениях дохода государства и дохода рыбака,
когда последний отклоняется (ненароком или умышленно) от своей локально
оптимальной стратегии. Приведем здесь два “неприятных” примера (Задорожный,
Ильичев 2006).
Пример стратегии доброго рыбака. Положим
)x1/(x8)x(F
+
=
и
. Рассмотрим две разные стратегии вылова - локально оптимальная
стратегия и “скромная” . Неожиданно оказывается, что
независимо от начального значения
)u1/(u)u(p +=
)x(u
*
)x(u75.0)x(u
*
1
=
x
при скромной стратегии глобальный доход
рыбака становится больше, а доход государства меньше. Разгадка этого
“парадокса” состоит в том, что при скромном управлении биомасса популяции
выходит на новый довольно высокий стационарный уровень . Здесь
выполняется неравенство , поэтому при
*
1
xx >
)x(u)x(u75.0
**
1
*
>
1≈
β
доход от
скромной стратегии больше.
Пример стратегии жадного рыбака. Пусть биомасса всей рыбной
популяции равна
x
, тогда ее стоимость (=капитал “государства”) равна B (x). Если
в начальный момент времени “рыбак” (руководствуясь неэкономическими
интересами) выловил всю рыбу, то налог составляет xB'(x). Для вогнутой
функции B(x) при условии
0)0(
=
B
всегда выполняется неравенство xB'(x) < B(x)
и, значит, “государство” терпит убытки. В данной ситуации более эффективной
является жесткая налоговая политика. А именно, в качестве налога можно взять
величину
)ux(B)x(B)u,x(H
−
−
=
, (2.3)
которая представляет собой разность стоимости популяции “до и после” вылова.
Для вогнутой функции
B
с условием
0)0(B
=
имеет место ,
поэтому здесь жесткий налог превосходит мягкий.
)x(uB)u,x(H
/
>
187
Теперь “рыбак” ежегодно решает следующую задачу:
по всем из [0, ]. (2.4)
)]u,x(H)u(pmax[
ttt
−
t
u
t
x
Отметим, что при вылове “рыбаком” всей популяции “государство” получает
полную компенсацию, поскольку налог будет равен .
)x(B
Из (2.4) следует, что при
Nx
≤
вылов по прежнему равен нулю, а при
N
x
>
управление положительно и удовлетворяет соотношению
B' (x-u) = p' (u). (2.5)
Полученное в (2.5) управление меньше вылова, определяемого (2.1).
Поэтому данная схема
не эквивалентна исходной оптимизационной задаче, но
более надежна. Отметим, что налог (2.3) можно представить в следующем виде
))1u(x(B...)1x(B)x(B)u,x(H
///
−−++−+≈ .
Следовательно, при жесткой схеме налогообложения вылов каждой единицы
рыбной биомассы внутри года сопровождается увеличением налога.
7.3. “Волшебная сила” внутренних цен:
от конкуренции при эксплуатации к кооперации
Пусть, например, два рыбака облавливают одну и ту же популяцию. Тогда
динамика биомассы рыбной популяции задается уравнением
(
)
tttt
vwxFx
−
−
=
+1
, (3.1)
где управления должны удовлетворять ограничениям , и
0≥
t
w 0≥
t
v
ttt
xvw
≤
+
;
F
- унимодальная функция с вогнутой левой ветвью.
Разумеется, «рыбаки» конкурируют друг с другом. Поэтому здесь возникает
проблема построения «справедливого» экономического механизма, регулирующего
их вылов. К решению данной задачи можно подойти несколько парадоксальным
образом. Обеспечение населения рыбной продукцией будет наибольшим (такая
ситуация выгодна государству), когда действия конкурирующих рыбаков
оказываются кооперативными. Можно ли этого добиться? Оказывается, можно,
если задать внутреннюю цену, исходя из кооперативных действий «рыбаков». В
